基于稀疏重构的L型阵列MIMO雷达降维DOA估计

2015-06-05梁浩，崔琛，代林，余剑

系统工程与电子技术 2015年12期

关键词：降维协方差重构

梁浩，崔琛，代林，余剑

（电子工程学院通信对抗系，安徽合肥230037）

基于稀疏重构的L型阵列MIMO雷达降维DOA估计

梁浩，崔琛，代林，余剑

（电子工程学院通信对抗系，安徽合肥230037）

针对L型阵列多输入多输出（multiple-input multiple-output，MIMO）雷达二维空间角估计问题，提出一种基于协方差矩阵联合稀疏重构的降维波达方向（direction of arrival，DOA）估计算法。该算法根据L型阵列MIMO雷达联合流型矢量的特点，通过降维矩阵的设计及回波数据的降维变换，最大程度地去除了所有的冗余数据；通过协方差矩阵联合构造稀疏线性模型，将2维角参量空间映射到1维空间，极大降低字典长度和求解复杂度的同时，不牺牲阵列孔径，实现了二维空间角度的有效估计和参数的自动配对。理论分析与实验仿真表明：与RD_MUSIC算法相比，本文降维处理有效提高阵元利用率的同时，最大程度地降低了回波数据的维数；与传统子空间类算法相比，基于协方差矩阵联合构造的稀疏线性模型充分利用了阵列孔径，无需预先估计目标数目，参数估计性能在低信噪比及小快拍数据长度下优势明显。最后，仿真结果验证了本文理论分析的正确性和算法的有效性。

多输入多输出雷达；L型阵列；稀疏重构；波达方向估计

0 引言

多输入多输出（multiple-input multiple-output，MIMO）雷达［1-2］能有效提高雷达参数识别性能［3］及目标空间分辨力；同时因其具有数字化、多通道化、低辐射等特点，已成为现代新型雷达发展趋势的综合体现和典型代表。目标角度估计［25］是雷达信号处理中一个重要的研究方向，目前对单基地MIMO雷达的研究大多仅限于一维参数估计；事实上，当收、发阵列均采用二维天线构型时，意味着目标参数维度的扩展，对目标的描述也就更准确，相应的参数估计也就更为复杂；在众多的平面天线构型中，L型阵列结构简单、阵列冗余度较小，能够实现空域目标二维角度定位，且已被证明具有优于其他交叉阵列结构的波达方向（direction of arrival，DOA）估计性能［67］；因此深入研究L型阵列MIMO雷达的参数估计问题具有重要意义和实用价值。

关于L型阵列MIMO雷达的研究主要集中在传统子空间类算法的扩展应用。文献［8- 9］基于单基地MIMO雷达研究了不同平面流型配置下阵列整体的流型敏感性以及阵元的重要程度，为MIMO雷达系统的天线设计提供了依据。文献［10］基于DOA矩阵思想，实现了目标二维角度的估计，并进一步提出联合对角化DOA矩阵方法解决了角度兼并问题；但该模型采用收发阵列垂直分置的L型配置，因此算法并不适用于收发均为L型阵列的共置MIMO雷达。文献［11］建立了L型阵列配置的单基地MIMO雷达，并基于MIMO-Capon算法实现了目标方位角和俯仰角的二维估计，但需要二维的谱搜索；文献［12］针对文献［11］算法计算复杂度较高的问题，提出一种基于MUSIC算法的L型阵列多输入多输出雷达降维DOA估计算法。算法通过构造降维矩阵对回波数据进行降维预处理后，利用二次优化方法将二维DOA估计分解为两个一维DOA估计，一定程度上降低了运算复杂度，但降维矩阵的设计并没有最大程度地降低回波数据的维数，没有去除所有重复的虚拟阵元，回波数据中仍存在冗余；此外在利用二次优化进行降维求解过程中，对方向向量中各元素的约束较弱［13］，造成估计精度较差，同时协方差矩阵的构建和特征分解以及两次一维谱搜索仍存在较高的运算量。

尽管传统子空间类算法能够实现二维空间角的有效估计，但普遍存在以下问题：①需要预先进行目标数目的估计，其准确性会严重影响后续子空间的划分及算法的性能；②需要多次脉冲的数据来提高与理论协方差矩阵的逼近程度，在低信噪比及有限数据长度下，对信号子空间的估计会存在较大偏差，使得估计精度和稳健性能严重恶化。利用远场目标的空域稀疏性，基于稀疏重构理论能够很好的解决以上问题，文献［14- 15］利用L型阵列的流型结构，通过二维稀疏线性模型分解和重新组合，利用其构造冗余字典可以将方位角和俯仰角的组合从2维空间映射到1维空间，极大降低字典的长度和求解的复杂度；文献［16］更是将这种思想推广到了频域，实现了宽频带内目标方位与频率的联合估计。以上算法本质上是基于阵列流型，将二维参量解耦合，分维两次基于传统一维稀疏重构算法实现二维参量的估计；当MIMO雷达收发均为L型阵列时，这类算法仅能利用到部分虚拟阵元，造成孔径的损失，这显然与MIMO雷达通过虚拟孔径提高分辨力的初衷是背驰的。本文针对L型阵列MIMO雷达二维空间角估计问题，提出一种降维预处理后基于协方差矩阵联合稀疏重构（reduceddimensional joint sparse recovery of covariance matrix，RD_ JSRCM）的L型阵列MIMO雷达DOA估计算法。

1 问题建模

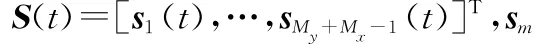
图1 L型阵列MIMO雷达结构及角度配置关系

远场空域内存在K个目标，第k（k＝1，2，…，K）个目标空间角为（ϑk，φk），满足cosϑ＝cosθcosφ，cosφ＝cosθsinφ；其中（θ，φ）对应目标的俯仰角与方位角，（ϑ，φ）对应目标分别与X、Y轴的夹角。则第q｛q＝1，…，Q｝次脉冲下接收端的输出为

对yq进行列堆栈，即可得到Q次脉冲下L型阵列MIMO雷达的回波接收数据：

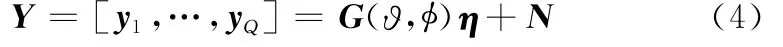
式中，η＝［β1，…，βQ］对应目标的散射系数；N＝［n1，…，nQ］

2 算法描述

2.1 接收数据降维预处理

L型阵列MIMO雷达虚拟扩展如图2所示，显然Mx＋My－1个实阵元经过MIMO雷达的虚拟扩展后，得到（Mx＋My－1）2个虚拟阵元，然而其中仅有MxMy＋Mx＋My－2为有效阵元，其余均为冗余阵元。则由信号模型可得

图2 虚拟扩展及示意图

式中

对应置换矩阵，构造方式与文献［12］类似；显然，g（ϑ，φ）与ρ（ϑ，φ）成线性关系，同时

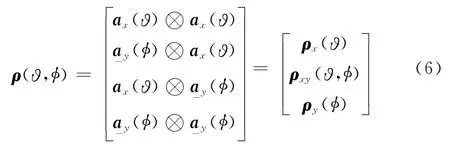
则存在以下线性变换

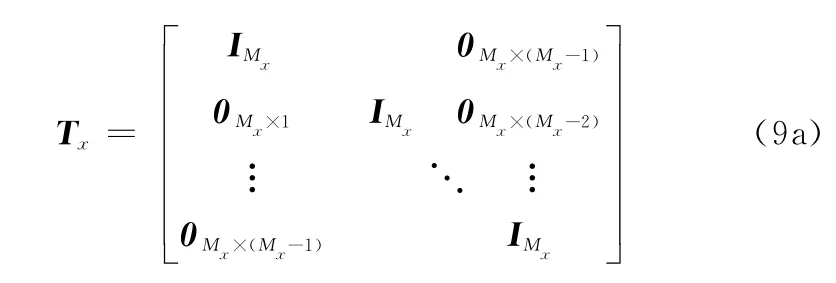
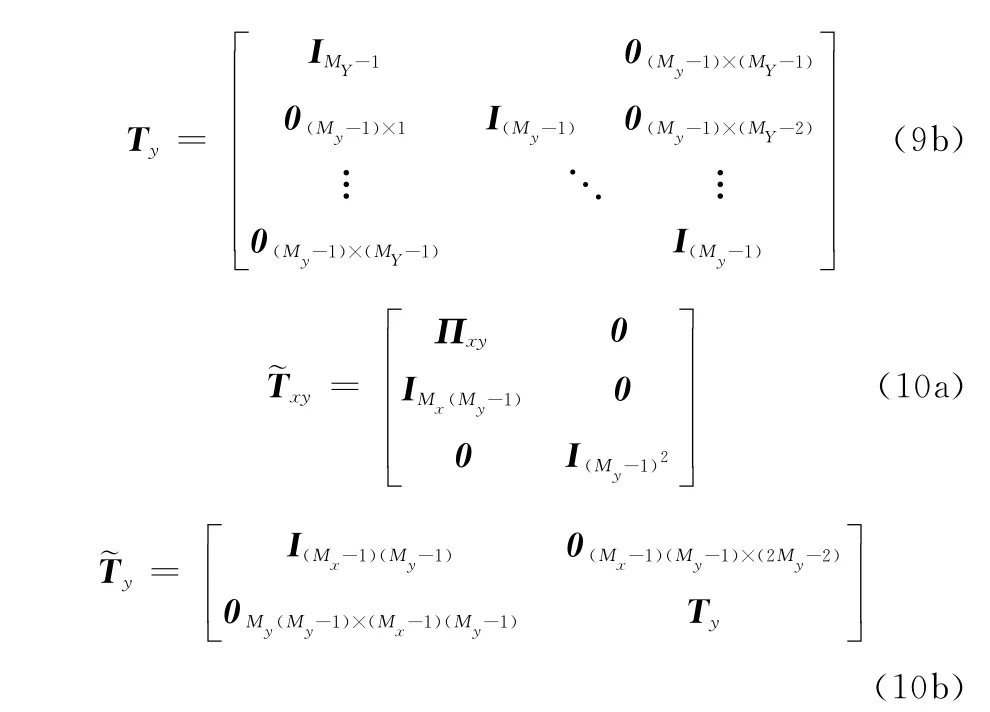
式中，Πxy为置换矩阵，与Πx、Πy类似。由式（5）、式（7）和式（8）可得，存在降维矩阵Γ满足

则式（4）中回波接收数据可表示为

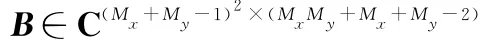
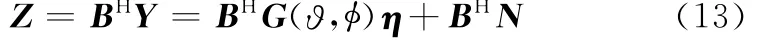
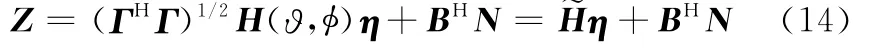
式（15）证明略。从式（14）、式（15）可得，降维后回波数据Z等效长度MxMy＋Mx＋My－2的加权平面阵的回波信号，权值为（ΓHΓ）1／2的对角元素。由H（ϑ，φ）及图2可知，本文通过设计降维矩阵，将（Mx＋My－1）2维的回波信号降至MxMy＋Mx＋My－2，去除了所有的重复阵元，而文献［12］降维多重信号分类（reduced-dimensional multiple signal classification，RD_MUSIC）RD_MUSIC算法仅仅是将（Mx＋My－1）2维的雷达回波信号降至MxMy＋Mx＋2My－4，降维后仍存在My－2个重复阵元。因此与之相比，本文降维预处理最大程度地降低了回波数据的维数，有效去除了原始回波数据中所有重复量，达到了降维的目的。

2.2 对称置换预处理

为后续处理方便，首先对降维后的回波数据Z进行权值归一化操作

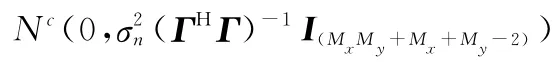
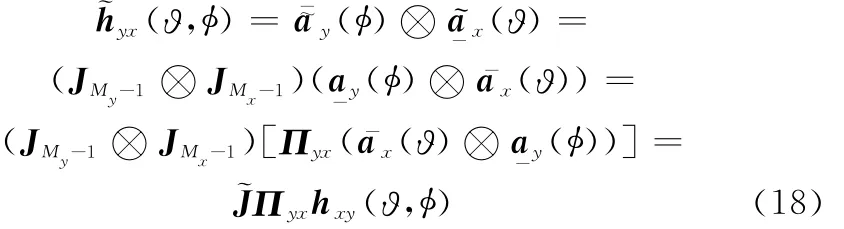
在得到预处理的回波数据Zx和Zy后，即可利用子空间类算法（如文献［12］RD_MUSIC、2D_MUSIC等）获取对信号子空间H（ϑ，φ）的估计，实现二维空间角的估计。考虑到子空间类算法在低信噪比及小数据快拍长度下估计性能较差的缺陷，利用远场空域目标稀疏的先验信息，将DOA估计转化为从测量矢量中重构稀疏信号的问题，能够获得目标方位信息的超分辨估计。直接构建二维过完备字典，则意味着后续高维复杂度的迭代重构；由图2可知，经过MIMO雷达虚拟后，阵列仍呈现为近似L型，通过二维稀疏线性模型分解和重新组合，利用其构造冗余字典可以将二维空间映射到一维空间，但问题是这样只能利用MIMO雷达的部分虚拟阵元（只利用到X轴上的2Mx－1阵元和Y轴上的2My－1阵元），降低了雷达整体的孔径利用率，从而不能很好发挥MIMO雷达的高分辨性能；为此本文利用预处理后的回波数据Zx和Zy构建相应的稀疏线性模型，提出一种基于协方差矩阵联合稀疏重构的L型阵列MIMO雷达降维DOA估计算法。

2.3 联合稀疏模型建立

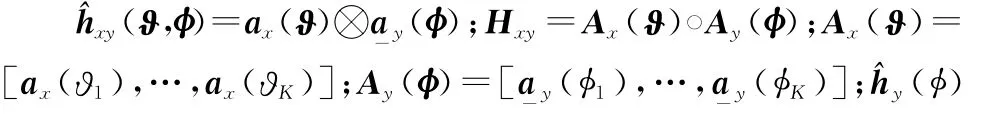
式中，Vx＝diag｛Wx｝。对Rxx进行列向量化操作得

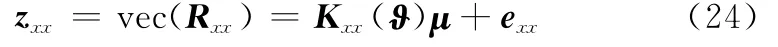
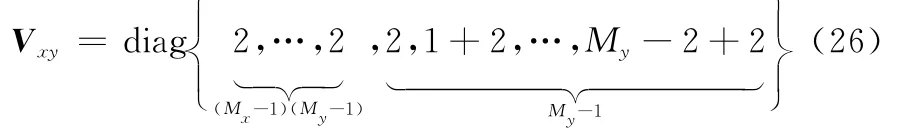
式中，k＝1，…，K；n＝1，…，Nx。则式（29）可以重写为

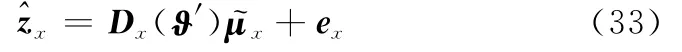
同样可以利用Zy构建角参量φ的稀疏线性模型

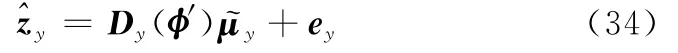
2.4 模型求解

式（33）和式（34）中，由于ex与ey均服从高斯分布，因此可以采用2范数来约束拟合误差，则稀疏线性模型的目标优化函数可表示为：

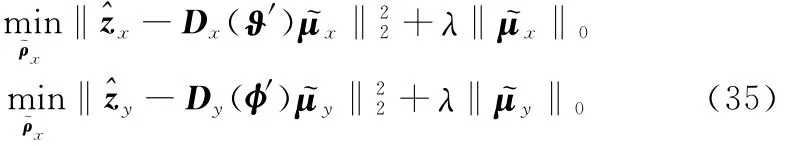
λ对应正则化参数，平衡控制着拟合误差与μ稀疏性，可以通过L-Curce、广义的SURE（generation SURE，GSURE）等方法进行调整和选取。直接求解式（35）是困难的，一方面考虑拟合误差服从高斯分布，可以采用文献［19］中的平滑零范数，通过一类高斯函数近似逼近零范数求解最小化问题，重构出相应的稀疏信号，但该方法重构性能以及精度与高斯函数和映射函数的选取相关；另一方面通过凸松弛类算法采用1范数来代替0范数进行凸松弛。本文考虑凸松弛类算法将非凸优化问题转化为以下的凸优化问题

可以分别利用内点法求解，考虑式（36）中参数均为复数，则对应的二阶锥规划形式可表示为

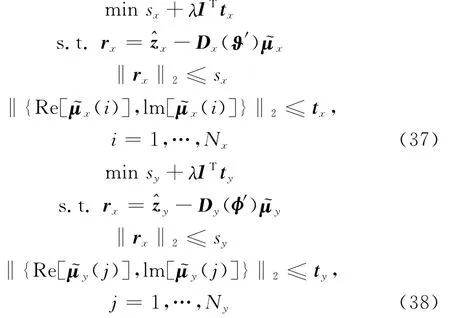
显然，关于角参量ϑ和φ的求解是分开进行的，得到对应的估计值和后，定义低维的联合过完备字典D（）为

可得重组后的联合稀疏线性模型为

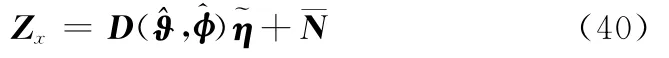
2.5 算法复杂度分析

本文降维预处理后采用文献［15］分维稀疏重构算法简称为RD_JEVSD；本文降维预处理后基于协方差矩阵联合稀疏重构的方法称为RD_JSRCM算法。RD_JEVSD与RD_JSRCM算法在后续基于凸松弛类算法求解过程中，算法复杂度相差不大，尽管两者构建的过完备字典的维数不同，但都要远小于完备字典的长度Nx和Ny，因此算法复杂度主要为O｛N＋N｝；而在稀疏线性模型构建过程中，RD _JEVSD算法仅利用到（L型阵列MIMO雷达虚拟扩展后的阵列）X、Y轴的等效回波数据，算法运算量集中在协方差矩阵计算及特征分解：O｛Q（2Mx－1）2＋Q（2My－1）2＋（2Mx－1）3＋（2My－1）3｝；对应的RD_JSRCM算法运算量集中在zx和zy构造中协方差矩阵的计算：O｛Q（2Mx－1）2＋Q（2My－1）2＋Q（Mx－1）2＋Q（My－1）2｝，因此两者的运算复杂度相当，但本文RD_JSRCM算法无需特征分解，不牺牲雷达孔径，最大程度地利用了虚拟阵列，因此在估计性能及稳健性方面更优。

3 仿真实验与分析

假设均匀配置下的L型阵列MIMO雷达，阵元间距满足dx＝dy＝λ／2，以多相码为正交发射信号，分别进行以下实验。

实验1 算法的有效性验证。不失一般性，假设阵元数满足Mx＝My＝8，远场空域存在K＝3个目标，与L型阵列MIMO雷达X、Y轴的夹角为（50°，60°），（70°，100°），（110°，120°）；信噪比为5 d B，快拍数Q＝200；进行100次蒙特卡罗实验，验证本文RD_JSRCM算法的有效性，其中过完备字典Dx（ϑ′）和Dy（φ′）均在（0°，180°）内以0.1°为间隔均匀采样构建而成，仿真结果如图3所示。图3（a）为100次蒙特卡罗实验后本文RD_JSRCM算法与文献RD_JEVSD算法的二维空间角的估计结果；图3（b）为本文RD_JSRCM算法二维空间角经过自动配对后的星座图。

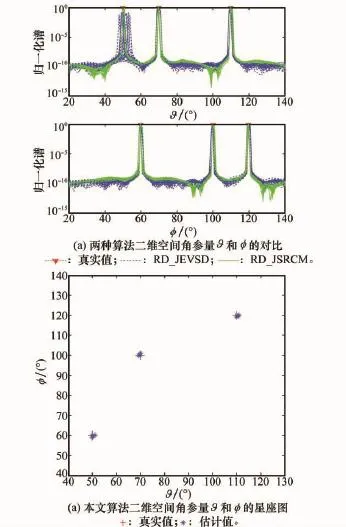
图3 目标二维空间参量ϑ和φ的估计结果

由图3可知，本文所提RD_JSRCM算法能够实现对目标二维空间角的有效估计，且能实现参数的自动配对；同时由图3也可以看出，与文献［15］RD_JEVSD算法相比，本文RD_JSRCM算法空间谱估计更为准确和稳健，空间角度位置星座图上的估计结果比较集中而没有出现散布，一定程度上也反映了本文算法的稳健性。

实验2 算法的估计性能比较。假设发射阵元数满足Mx＝My＝6，远场空域目标位置及个数不变；快拍数Q＝50，信噪比－10～30 dB，比较2D_MUSIC、RD_MUSIC、RD_JEVSD以及本文RD_JSRCM算法的估计性能，其中2D_MUSIC与文献［12］RD_MUSIC算法的谱搜索步长均为0.1°，RD_JEVSD及本文RD_JSRCM算法的过完备字典构造均以0.1°为间隔采样，仿真结果如图4所示。

图4 目标二维空间角估计的RMSE与SNR的关系

由图4可以看出，随着信噪比（signal-to-noise ratio，SNR）的增大，4种算法对目标二维空间角估计的均方根误差（root mean square error，RMSE）都逐渐变小，且信噪比越大，估计精度越高，这一点很好理解；同时与子空间类算法（2D_MUSIC和RD_MUSIC算法）相比，基于稀疏重构理论的RD_JEVSD和RD_JSRCM算法在低信噪比时，估计性能较优，高信噪比时角度估计性能趋于一致；与RD_JEVSD算法仅利用到X、Y轴（L型阵列MIMO雷达虚拟扩展后的阵列）的等效回波数据相比较，本文提出的RD_JSRCM算法基于协方差矩阵联合构建稀疏模型，利用到了所有阵元回波数据，最大程度地利用了阵列孔径，具有更高的估计性能。此外本文RD_JSRCM算法通过降维处理，去除所有重复项的同时，并没有改变噪声特性，保留了所有的目标信息，在利用降维处理后回波数据构建联合稀疏模型时，权值归一化操作，一定程度上也降低了噪声的影响，提高了参数估计性能。

实验3 算法的性能与参数之间的关系。空域目标位置、个数与实验2相同，快拍数Q＝50，阵元数Mx＝My＝4～12时，信噪比为5 dB，比较不同阵元配置本文RD_JSRCM算法与文献RD_JEVSD算法的估计性能，仿真结果如图5所示。阵元数满足Mx＝My＝6，Q＝50～500变化，比较不同快拍数据下本文RD_JSRCM算法与文献RD_JEVSD算法的估计性能，仿真结果如图6所示。由图5、图6可以看出，随着阵元数Mx，My的增大，对应阵列雷达孔径也逐渐变大，因此两种算法对二维空间角的估计性能也越好；随着快拍数Q的增大，统计意义上稀疏模型的构建也就越准确，重构精度也就越高，因此角估计性能也就更好。同时由图5、图6的仿真结果可以看出，由于本文RD_ JSRCM算法利用了MIMO雷达所有虚拟阵元，没有牺牲阵列孔径，因此估计性能要优于文献RD_JEVSD算法。

图5 二维空间角估计的RMSE随阵元数的变化

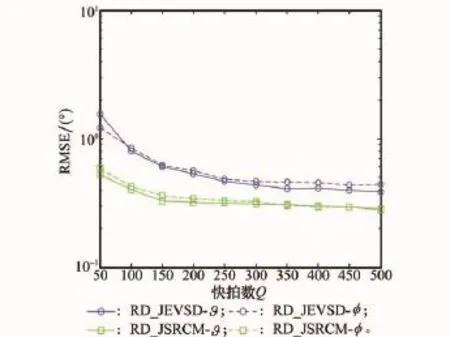
图6 二维空间角估计的RMSE随快拍数Q的变化

4 结论

本文针对L型阵列MIMO雷达二维空间角估计问题，提出一种基于协方差矩阵联合稀疏重构的L型阵列MIMO雷达降维DOA估计算法。理论分析与仿真表明：①与文献RD_MUSIC算法相比，本文算法通过降维矩阵的设计及回波数据的降维变换，最大程度地降低了回波数据的维数，进一步降低了所需处理的回波的数据量，有效提高了阵元的利用率；②基于协方差矩阵联合的稀疏线性模型，将二维角参量空间映射到一维空间，极大降低字典长度和求解复杂度的同时，充分利用阵列孔径，实现了二维参量的联合估计及参数的自动配对；③与传统子空间类算法相比，本文算法无需预先估计目标数目，估计性能在低信噪比及小快拍数据长度下优势明显。

［1］Huleihel W，Tabrikian J，Shavit R.Optimal adaptive waveform design for cognitive MIMO radar［J］.IEEE Trans.on Signal Processing，2013，61（20）：5075- 5089.

［2］Tang B，Tang J，Zhang Y，et al.Maximum likelihood estimation of DOD and DOA for bistatic MIMO radar［J］.Signal Processing，2013，93（5）：1349- 1357.

［3］Arash K.Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar［J］.IEEE Trans.on Signal Processing，2014，62（6）：1490- 1500.

［4］Li J F，Zhang X F.A method for joint angle and array gain-phase error estimation in bistatic multiple input multiple output nonlinear arrays［J］.IET Signal Processing，2014，8（2）：131- 137.

［5］Jiang H，Zhang Y，Li J，et al.A parafac-based algorithm for multi-dimensional parameter estimation in polarimetric bistatic MIMO radar［J］.EURASIP Journal on Advances in Signal Processing，2013，2013（1）：1- 14.

［6］Cheng Q，Hua Y.Further study of the pencil-MUSICalgorithm［J］.IEEE Trans.on Aerospace Electronic Systems，1996，32（1）：284- 299.

［7］Hua Y，Sarkar K，Weiner D.An L-shaped array for estimation 2-D directions of wave arrival［J］.IEEE Trans.on Antennas and Propagation，1991，39（2）：143- 146.

［8］Chen H W，Li X，Jiang W D，et al.MIMO radar sensitivity analysis of antenna position for direction finding［J］.IEEE Trans.on Signal Processing，2012，60（10）：5201- 5216.

［9］Chen H W，Zhou W，Yang J，et al.Manifold sensitivity analysis for MIMO radar［J］.IEEE Geoscience and Remote Sensing Letters，2012，9（5）：999- 1003.

［10］Fu W B，Zhao Y B，Su T，et al.DOA matrix method based on MIMO radar with L-shape arrays［J］.Journal of Systems Engineering and Electronics，2011，33（11）：2398- 2403.（符渭波，赵永波，苏涛，等.基于L型阵列MIMO雷达的DOA矩阵方法［J］.系统工程与电子技术，2011，33（11）：2398- 2403.）

［11］Xie R，Liu Z，Liu Y F.Multi-target identification and localization in MIMO radar with L-shape arrays［J］.Systems Engineering and Electronics，2010，32（1）：49- 52.（谢荣，刘铮，刘韵佛.基于L型阵列MIMO雷达的多目标分辨和定位［J］.系统工程与电子技术，2010，32（1）：49- 52.）

［12］Wang W，Wang X M，Li X，et al.Reduced-dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array［J］.Journal of Electronics&Information Technology，2014，36（8）：1954- 1959.（王伟，王晓萌，李欣，等.基于MUSIC算法的L型阵列MIMO雷达降维DOA估计［J］.电子与信息学报，2014，36（8）：1954- 1959.）

［13］Cai J J，Bao D，Li P，et al.Two-dimensional DOA estimation using reduced-dimensional MUSIC algorithm with strong-constraint optimization［J］.Journal of Electronics&Information Technology，2014，36（5）：1113- 1118.（蔡晶晶，鲍丹，李鹏，等.强约束优化降维MUSIC二维DOA估计［J］.电子与信息学报，2014，36（5）：1113- 1118.）

［14］Wang L B，Cui C.L-shaped array-based two dimensional direction-of-arrival estimation in a sparse reconstruction framework［J］.Journal of Astronautics，2012，33（7）：964- 970.（王粒宾，崔琛.基于稀疏重构的L型阵列的二维波达方向估计［J］.宇航学报，2012，33（7）：964- 970.）

［15］Cui C，W L B.L-shaped array-based joint elevation and azimuth direction finding by spatial sparsity［J］.Journal of Circuits and Systems，2013，18（1）：297- 303.（崔琛，王粒宾.利用空域稀疏性的L型阵下二维波达方向估计［J］.电路与系统学报，2013，18（1）：297- 303.）

［16］Li P F，Zhang M，Zhong Z F.Two dimensional DOA estimation based on sparse representation of space angle［J］.Journal of Electronics&Information Technology，2011，33（10）：2402- 2406.（李鹏飞，张旻，钟子发.基于空间角稀疏表示的二维DOA估计［J］.电子与信息学报，2011，33（10）：2402 -2406.）

［17］Zhang X，Xu D.Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced-dimension transformation［J］.Eletronics Letters，2011，17（47）：283- 284.

［18］Liao B，Chan S C.Direction finding with partly calibrated uniform linear arrays［J］.IEEE Trans.on Antennas and Propagation，2012，60（2）：922- 929.

［19］Hyder M M，Mahata K.An improved smoothed L0 approximation algorithm for sparse representation［J］.IEEE Trans.on Signal Processing，2010，58（4）：2194- 2205.

Reduced-dimensional DOA estimation based on sparse reconstruction in MIMO radar with L-shaped array

LIANG Hao，CUI Chen，DAI Lin，YU Jian
（Department of Communication Countermeasure，Electronic Engineering Institute，Hefei 230037，China）

Aiming at the problem of two dimensional angles estimation for multiple-input multiple-output（MIMO）radar with L-shaped array，a new reduced-dimensional direction of arrival（DOA）estimation method based on sparse reconstruction is proposed.Giving the steering vector of MIMO radar with L-shaped array，a reduced-dimensional matrix is employed，and data redundancy of high dimensional

data at the greatest degree can be removed via the reduced-dimensional transformation.Through the joint construction of the twodimensional sparse linear model with covariance matrix，the dimension of the dictionary is reduced to one-dimension from two-dimensional space，and the length of the redundant dictionary and computation complexity is largely reduced.Furthermore，the method，without costing the aperture of array，can realize two dimensional spatial angles estimation with automatic pairing.Compared with reduced-dimensional（RD）MUSIC，the proposed method can reduce the dimension of received data at the greatest degree and enhance sensors efficiency.Compared with the traditional subspace algorithms，the proposed method，which is based on the joint sparse linear model of the covariance matrix，makes the best of all apertures of array and can achieve better estimation performance under lower signal-noise-ratio（SNR）and a few snapshots without pre-estimation for the number of targets.Finally，simulation results verify the correctness of the theoretical analysis and the effect of the proposed algorithm.

multiple-input multiple-output（MIMO）radar；L-shaped array；sparse reconstruction；direction of arrival（DOA）estimation

TN 958

10.3969／j.issn.1001-506X.2015.12.10

梁浩（198-7- ），男，博士研究生，主要研究方向为阵列信号处理以及MIMO雷达信号处理。

E-mail：lhmailhappy＠163.com

崔琛（196-2- ），男，教授，博士研究生导师，主要研究方向为雷达信号处理。

E-mail：kycuichen＠163.com

代林（198-6- ），男，博士研究生，主要研究方向为压缩感知雷达信号处理。

E-mail：dailin513＠163.com

余剑（1980- ），男，讲师，博士，主要研究方向为雷达信号处理、射频信号处理。

E-mail：yujianeei＠163.com

1001-506X（2015）12-2725-08