多模型标签多伯努利机动目标跟踪算法

2015-06-05黄高明

系统工程与电子技术 2015年12期

关键词：伯努利杂波航迹

邱昊，黄高明，左炜，高俊

（海军工程大学电子工程学院，湖北武汉430033）

多模型标签多伯努利机动目标跟踪算法

邱昊，黄高明，左炜，高俊

（海军工程大学电子工程学院，湖北武汉430033）

针对标准标签多伯努利（labeled multi-Bernoulli，LMB）算法只考虑了单个运动模型的问题，提出了一种适用于跳转马尔科夫系统的多模型标签多伯努利（multiple model LMB，MM-LMB）算法。首先对目标状态进行扩展，将多模型思想引入LMB算法得到了新的预测和更新方程，并给出了算法的序贯蒙特卡罗实现。仿真实验表明，MM-LMB算法能对多机动目标进行有效跟踪，在复杂探测环境下跟踪精度优于多模型概率假设密度（multiple model probability hypothesis density，MM-PHD）算法和多模型势平衡多目标多伯努利（multiple model cardinality balanced multi-target multi-Bernoulli，MM-CBMe MBer）算法；所提算法计算量当目标相距较远时低于MM-PHD和MM-CBMe MBer，目标聚集时增长速度快于对比算法。

多目标跟踪；机动目标；标签多伯努利；序贯蒙特卡罗

0 引言

随着无源探测技术的快速发展，复杂环境下多目标跟踪技术成为研究的热点。在低信噪比探测环境中，传统多目标跟踪算法的数据关联过程导致计算和存储负荷快速增长，限制了算法的应用范围。另一方面，传统多目标算法在低信噪比环境下的良好性能对多目标跟踪技术的发展仍具有启发意义。

针对上述问题，国内外学者做出了许多有益的探索。基于随机有限集（random finite set，RFS）理论的概率假设密度（probability hypothesis density，PHD）［1］算法结构简洁，同时避免了复杂的关联过程而成为研究热点。针对PHD算法对漏警敏感的问题，文献［2］提出了基于高阶矩近似的势概率假设密度（cardinalized PHD，CPHD）算法，改善了原算法目标数估计性能。此外，文献［3］提出了基于伯努利模型的多目标多伯努利（multi-target multi-Bernoulli，MeMBer）算法。通过序贯蒙特卡罗（sequential Monte Carlo，SMC）方法实现算法时，MeMBer滤波器避免了不稳定且计算开销大的聚类过程［4］。由于在推导过程中采取了不严谨的近似步骤［5］，MeMBer算法存在目标数估计不准的问题。文献［6］提出了势平衡多伯努利（cardinality balanced MeMBer，CBMeMBer）算法，改善了原算法势过估的问题。针对上述RFS算法在低信噪比环境下性能严重下降的问题，文献［7- 8］结合多假设跟踪算法和随机集统计理论，提出了Delta扩展标签多伯努利（δ-generalized labeled multi-Bernoulli，δ-GLMB）算法，并给出了该算法的SMC和高斯混合（Gaussian mixture，GM）实现方法。同多假设算法类似，δ-GLMB同样面临假设快速增长带来的计算压力。针对该问题，文献［9］提出的LMB改进算法通过假设合并及航迹分组等近似方法大大降低了算法的计算量。

多模型（multiple model，MM）算法是处理机动目标的有效方式之一。近年来，已有文献提出了基于MM算法和RFS滤波器的多机动目标跟踪算法［1016］。由于PHD／CPHD、Me MBer／CBMeMBer固有的局限性，此类算法在低信噪比探测环境下性能严重下降。针对此问题，本文将MM系统引入LMB算法，提出了一种适用于多机动目标跟踪的MM-LMB算法，并给出了算法的SMC实现。仿真实验验证了MM-LMB算法在低信噪比探测环境下机动多目标跟踪的良好性能。

1 LMB算法及多模型系统

1.1 LMB滤波器

随机有限集中的随机变量处于无序状态，对集合中各元素添加标签索引是解决该问题的有效方法。标签RFS将目标状态扩展为X＝｛（xi，li）｝（i＝1，2，…，｜X｜），xi∈Ω表示单目标状态，Ω为目标状态空间；l∈L是与目标状态独立的标签，L为标签空间；｜·｜代表集合的势。标签多伯努利RFS由若干独立的标签伯努利RFS构成，概率分布为

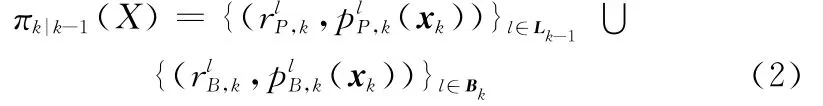
记k时刻量测RFS为Zk，预测分布重写为πk｜k－1（X）＝，LMB滤波器后验分布可以近似为LMB过程，其概率分布为

式中

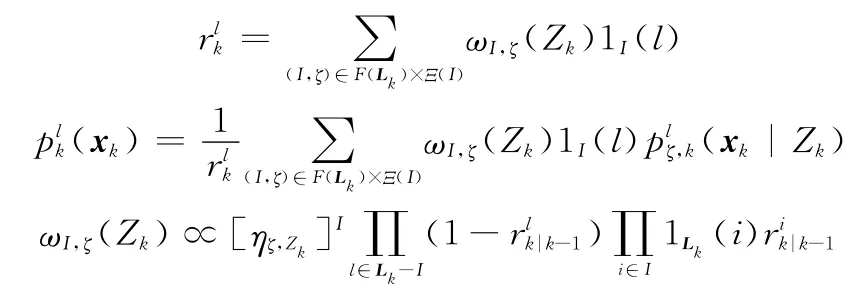
式中，F（·）表示子空间划分函数；ζ∈Ξ（I）表示由标签到量测的关联：I→｛0，1，…，｜Zk｜｝，0代表量测为空，且ζ（l）＝ζ（l′）＞0时l＝l′；Ξ（I）为关联集合；（x）为探测概率；（z｜x）为似然函数，z∈Zk；κk（z）为杂波分布；1L（l）为指示函数。

1.2 多模型系统

多模型算法是处理跳转马尔科夫（jump Markov，JM）系统的有效方法，其系统动态方程与模型有关

式中，nk∈Π为模型索引，Π＝｛1，…，｜Π｜｝为模型索引集合；~fk｜k－1和分别是与模型相关的状态转移函数和似然函数；和分别为过程噪声和观测噪声。目标运动模型转换满足马尔科夫过程，在线性JM系统中，模型转移概率a（nk｜nk－1）为常数。

2 多模型粒子LMB滤波算法

2.1 MM-LMB滤波器

为了得到MM-LMB滤波器，首先对目标状态进行扩展x～＝（x，l，n），扩展LMB分布为

包含模型信息的状态转移方程和观测方程分别为

与多模型粒子滤波类似，MM-LMB算法在递推多目标状态的同时也对目标运动模型进行预测及修正，具体步骤如下。

步骤1预测。假设k－1时刻多目标后验分布满足式（6），新生目标是LMB过程，则MM-LMB预测分布为

需要注意的是，多模型系统中扩展目标状态的内积函数为多维积分

已知。

式中

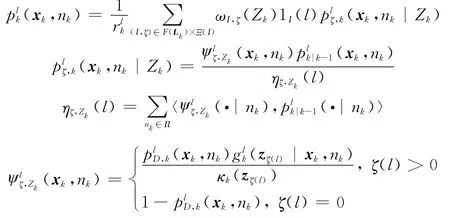
2.2 MM-LMB的SMC实现

由式（9）可直接得到

式中，q（·｜xk－1，l，nk－1，Zk），b（·｜Zk）分别为存活和新生目标的建议分布函数。

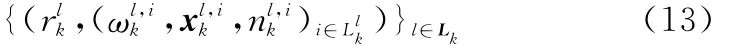
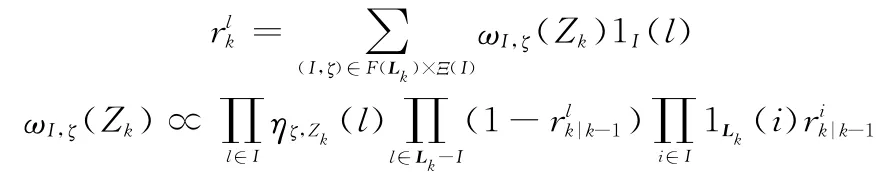
与LMB类似，MM-LMB使用了假设分组和LMB与δ-GLMB转换等近似方法来减少计算量；在δ-GLMB更新过程中，采用了K最短路径和Murty排序算法限制假设数目，具体过程可参考文献［8］。粒子MM-LMB算法递推了目标的全概率分布，因此在目标状态提取时避免了聚类过程。另外，对权值归一化后的粒子进行重采样能有效改善粒子退化问题。

3 仿真分析

3.1 环境设置

多个机动目标（单位：m）在［－1 000，1 000］×［－1 000，1 000］的观测区域内运动，运动模型集由一个近匀速运动（nearly constant velocity，NCV）模型和一个协同转弯（coordinated turn，CT）模型构成。运动方程为

（1）NCV模型

（2）CT模型

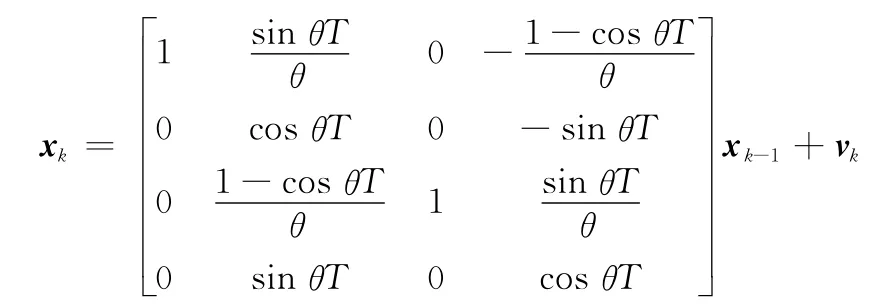
式中，目标状态x＝［x，x·，y，y·］T包含了位置和速度信息；假设过程噪声vk与模型独立且服从零均值高斯分布，协方差矩阵为

噪声标准差δv＝0.5 m／s；转弯速率θ＝5π／180 rad／s；模型转换概率矩阵

式中，模型驻留时间τNCV＝10 s，τCT＝5 s；观测周期T＝1 s，观测过程持续100 s。假设系统观测方程与模型相独立

新生目标概率分布为

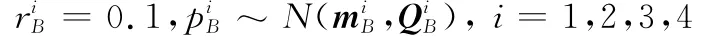
3.2 结果分析

仿真1场景中目标的新生、消亡及模型切换均具有不确定性，观测区域内至多同时存在8个目标，目标初始状态分别为［－830，10，200，－8］T，［597，－8，622，－9］T，［100，6.5，－900，12］T，［230，－6，460，－10］T以及和。单次实验目标真实航迹和量测如图1所示。

图1 真实航迹和量测

图2对比了所提算法与原算法平均势估计结果。可以看出当目标开始机动时（10 s，25 s和35 s），SMC-LMB出现明显的航迹丢失；另一方面，SMC-MM-LMB可以对目标进行有效跟踪，在探测条件较理想（pD＝0.98，λc＝10，δw＝5 m／s）时能对目标数进行无偏估计。

图2 SMC-LMB和SMC-MM-LMB目标数估计结果

为了更充分验证所提算法性能，基于运算量考虑，对比了MM-PHD，MM-CBMe MBer和MM-LMB算法在低信噪比环境下跟踪性能。图3对比了不同算法在低探测概率环境（pD＝0.8，λc＝10，δw＝5 m／s）下的平均势估计和OSPA距离。图3（a）说明了不同算法的势估计均出现了偏差，主要是因为漏警的频繁出现容易导致航迹丢失。同时，从图3（b）可以看出漏警对MM-LMB的影响要小于其他两种算法，这主要是因为PHD假设目标数服从泊松分布，对漏警敏感；在CBMe MBer推导过程中假设pD≈1，因此该算法不适用于低探测概率环境；LMB每帧滤波输出包含多个假设，并利用多帧量测信息计算假设概率，抗干扰性能良好，代价是算法对目标消失反应速度下降。

图3 低探测概率时目标数估计结果和OSPA距离

图4和图5分别说明了不同算法在强杂波（pD＝0.98，λc＝60，δw＝5 m／s）和高探测误差（pD＝0.98，λc＝10，δw＝30 m／s）环境下平均OSPA距离。可以看出，杂波密集和探测误差较大时，MM-LMB性能均优于MM-PHD和MM-CBMe MBer。多伯努利算法递推了目标完整的概率分布而非其矩近似，在SMC实现时避免了不稳定的聚类过程，因此MM-PHD更易受杂散影响；另一方面，在量测关联步中，MM-LMB继承了能利用多帧信息的多假设思想而MM-CBMeMBer采用了一种启发式的管理方法，因此MM-LMB在复杂量测环境中性能优于MM-CBMeMBer。

图4 强杂波环境下OSPA距离

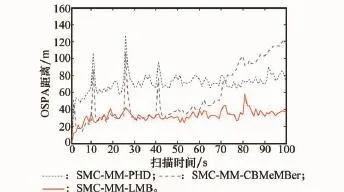
图5 高探测误差环境下OSPA距离

当目标数一定时，MM-PHD和MM-CBMeMBer计算复杂度均为O（｜Z｜），MM-LMB计算复杂度极限情况为O（｜Z｜3）［8］。通过适当的航迹删除和假设裁剪能有效降低伯努利滤波器的计算量。本文航迹存在概率门限为0.001，假设数目最大值1 000，分组时马氏距离门限值为1。在一台普通配置笔记本平台上，不同杂波密度下3种算法单次迭代平均运算时间如表1所示。可以看出，当杂波密度增加时，3种算法计算开销均有一定幅度增长。由于避免了聚类过程，两种多伯努利滤波器计算量明显小于MM-PHD；当杂波密度较低时，MM-LMB计算量略小于MM-CBMe MBer，随着杂波密度增加，前者计算时间增长速度慢于后者。

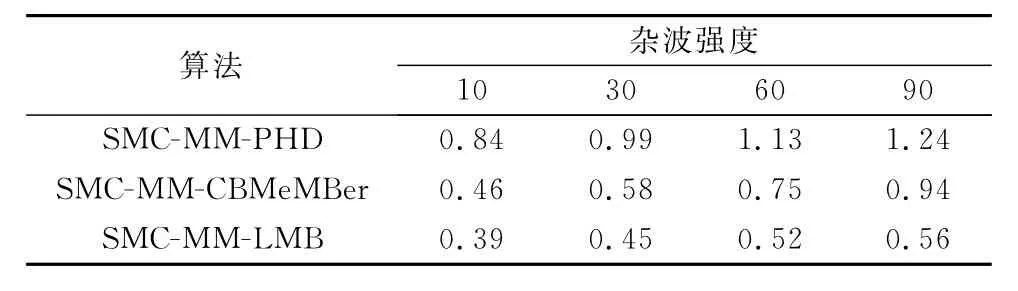
表1 算法平均运行时间比较 s

仿真2为了更充分验证算法性能，考虑了一种目标聚集场景。仿真2中，在1～5 s和30～35 s时间段内若干目标分别从和出现，区域内最多同时存在9个目标。探测环境参数为pD＝0.98，λc＝10，δw＝5 m／s；滤波器初始状态为0；其他条件与仿真1一致。MM-LMB单次蒙特卡罗仿真估计结果如图6所示。

图7对比了3种算法100次仿真的平均OSPA距离。在更新步中，MM-CBMe MBer使用了基于最大似然思想的量测管理策略，在处理近距离目标时稳定性差，易出现目标丢失［5，16］。另一方面，MM-LMB和MM-PHD的OSPA距离均明显小于MM-CBMe MBer，且随着目标数量的增多和聚集度的提高，MM-LMB要优于MM-PHD，说明跟踪近距离机动目标时MM-LMB比MM-PHD精度更高。

图7 3种算法的平均OSPA距离

不同算法在观测时间内平均单步运行时间如图8所示。可以看出，整个观测过程MM-PHD计算开销和目标数近似呈线性关系；在目标新生阶段，MM-LMB计算量快速增加，明显高于MM-PHD，主要因为目标相距较近时，航迹分组作用弱化，分组内假设关联数快速增长；随着目标逐渐分散，MM-LMB计算量快速下降，由于避免了聚类过程，在20～30 s和60～100 s时间段所提算法计算开销要小于MM-PHD。MM-CBMeMBer由于目标丢失严重故计算量最小。

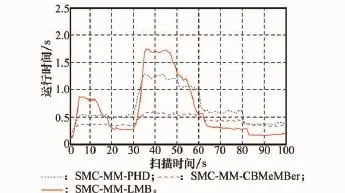
图8 3种算法平均单步运行时间

4 结论

将多模型思想和LMB算法相结合，提出了一种适应跳转马尔科夫系统的扩展LMB算法。实验表明在高信噪比探测条件下，MM-LMB能对机动目标进行有效跟踪，对目标数进行无偏估计；在低探测概率、强杂波和高探测误差等低信噪比条件下，MM-LMB目标状态和目标数估计精度优于MM-PHD和MM-CBMeMBer；当目标分散时，MM-LMB计算代价优于MM-PHD；随着目标聚集度的增加，所提算法计算开销增速明显快于MM-PHD。

［1］Mahler R.Multitarget Bayes filtering via first-order multitarget moments［J］.IEEE Trans.on Aerospace and Electronic Systems，2003，39（4）：1152- 1178.

［2］Mahler R.PHD filters of higher order in target number［J］.IEEE Trans.on Aerospace and Electronic Systems，2007，43（4）：1523- 1543.

［3］Mahler R.Statistical multisource multitarget information fusion［M］.Boston：Artech House，2007.

［4］Zhong Q Y，Ji H B，Ouyang C.Passive multi-target tracking based on modified Me MBer filter［J］.Systems Engineering and Electronics，2012，34（8）：1549- 1554.（钟茜怡，姬红兵，欧阳成.基于修正贝努利滤波的被动多目标跟踪算法［J］.系统工程与电子技术，2012，34（8）：1549- 1554.）

［5］Mahler R.“Statistics 102”for multisource-multitarget detection and tracking［J］.IEEE Journal of Selected Topics in Signal Processing，2013，7（3）：376- 389.

［6］Vo B T，Vo B N，Cantoni A.The cardinality balanced multitarget multi-Bernoulli filter and its implementations［J］.IEEE Trans.on Signal Processing，2009，57（2）：409- 423.

［7］Vo B T，Vo B N.Labeled random finite sets and multi-object conjugate priors［J］.IEEE Trans.on Signal Processing，2013，61（13）：3460- 3475.

［8］Vo B N，Vo B T，Phung D.Labeled random finite sets and the Bayes multi-target tracking filter［J］.IEEE Trans.on Signal Processing，2014，62（24）：6554- 6567.

［9］Reuter S，Vo B T，Vo B N，et al.The labeled multi-Bernoulli filter［J］.IEEE Trans.on Signal Processing，2014，62（12）：3246- 3260.

［10］Punithakumar K，Kirubarajan T，Sinha A.Multiple model multi-Bernoulli filters for maneuvering targets［J］.IEEE Trans.on Aerospace and Electronic Systems，2008，44（1）：87- 98.

［11］Pasha S A，Vo B N，Tuan H D，et al.A Gaussian mixture PHD filter for jump Markov system models［J］.IEEE Trans.on Aerospace and Electronic Systems，2009，45（3）：919- 936.

［12］Georgescu R A，Willett P K.The multiple model CPHD tracker［J］.IEEE Trans.on Signal Processing，2012，60（4）：1741- 1751.

［13］Dunne D，Kirubarajan T.Multiple model multi-Bernoulli filters for maneuvering targets［J］.IEEE Trans.on Aerospace and Electronic Systems，2013，49（4）：2679- 2692.

［14］Yang J L，Ji H B，Ge H W.Multi-model particle cardinalitybalanced multi-target multi-Bernoulli algorithm for multiple maneuvering target tracking［J］.IET Radar，Sonar and Navigation，2013，7（2）：101- 112.

［15］Ouyang C，Ji H B，Guo Z Q.Improved multiple model particle PHD and CPHD filters［J］.Acta Automatic Sinica，2012，38（3）：341- 348.（欧阳成，姬红兵，郭志强.改进的多模型粒子PHD和CPHD滤波算法［J］.自动化学报，2012，38（3）：341- 348.）

［16］Lian F，Han C Z，Li C.Multiple-model GM-CBMe MBer filter and track continuity［J］.Acta Automatic Sinica，2014，40（2）：336- 347.（连峰，韩崇昭，李晨.多模型GM-CBMe MBer滤波器及航迹形成［J］.自动化学报，2014，40（2）：336- 347.）

Multiple model labeled multi-Bernoulli filter for maneuvering target tracking

QIU Hao，HUANG Gao-ming，ZUO Wei，GAO Jun
（College of Electronic Engineering，Naval University of Engineering，Wuhan 430033，China）

For the problem that the standard labeled multi-Bernoulli（LMB）filter only considers the single motion model case，a multiple model LMB（MM-LMB）filter for maneuvering target tracking is proposed.By introducing the jump Markov（JM）system to the LMB method，the extended recursion formulations are presented，and the sequential Monte Carlo implementation of the proposed method is given.Simulations show that the MM-LMB filter can track multiple maneuvering targets effectively，and has higher tracking accuracy than the multiple model probability hypothesis density（MM-PHD）filter and the multiple model cardinality balanced multi-target multi-Bernoulli（MM-CBMe MBer）filter in complex detection environment.The calculation cost of the proposed method is lower than MM-PHD and MM-CBMe MBer when the targets are not closed，while grows faster than the compared algorithms when the targets gather together.

multi-target tracking；maneuvering target；labeled multi-Bernoulli（LMB）；sequential Monte Carlo

TN 953

10.3969／j.issn.1001-506X.2015.12.03

邱昊（198-8-- ），男，博士研究生，主要研究方向为多目标跟踪技术。

E-mail：qhcs01＠163.com

黄高明（197-2-- ），男，教授，博士，主要研究方向为无源探测和电子对抗技术。

E-mail：hgaom_paper＠163.com

左炜（1979-- ），男，讲师，博士，主要研究方向为雷达信号处理。

E-mail：zwei_wh＠163.com

高俊（195-7-- ），男，教授，博士，主要研究方向为无线通信和通信信号处理。

E-mail：gaojnj＠163.com

1001-506X（2015）12-2683-06