基于PSO的ML-PDA算法及其并行实现

2015-06-05高林，唐续，魏平

系统工程与电子技术 2015年12期

关键词：杂波线程全局

高林，唐续，魏平

（电子科技大学电子工程学院，四川成都611731）

基于PSO的ML-PDA算法及其并行实现

高林，唐续，魏平

（电子科技大学电子工程学院，四川成都611731）

针对密集杂波条件下的目标检测与跟踪问题，开展极大似然-概率数据关联（maximum likelihoodprobabilistic data association，ML-PDA）算法优化与实时计算问题研究。在算法层面，通过在极大化对数似然比（log likelihood ratio，LLR）过程中引入粒子群优化（particle swarm optimization，PSO）方法，并进一步提出基于观测引导的PSO播撒粒子方式，提升算法的计算效率；在实现层面，提出基于图形处理器（graphic processing unit，GPU）的PSO实现策略。仿真实验结果说明了基于观测引导PSO算法搜索的有效性。在GPU平台上实现该算法获得显著的加速比，验证了所提出方法具有工程实时性。

检测前跟踪；极大似然概率数据关联；粒子群优化；并行处理

0 引言

高密度杂波环境中的极低可观测目标跟踪问题一直是困难的研究热点。极低可观测意味着目标回波信号中信号能量与噪声功率比值，即信噪比（signal-to-noise ratio，SNR）很低。在传统的检测后跟踪（track after detect，TAD）算法中，若要维持对低SNR目标的高检测概率，势必会降低检测算法的检测门限。然而，这将导致更多的杂波，使得虚警概率上升，导致后续跟踪算法对目标的跟踪精度下降，甚至失效。

处理极低可观测目标跟踪的一类重要方法是检测前跟踪（track before detect，TBD），即同时实施目标的状态估计与检测。TBD与TAD的主要区别在于，前者使用未经过门限的原始数据，或门限设置很低的观测数据，以保证目标的高检测概率。TBD算法分两大类：①基于迭代的TBD算法，如TBD框架下的粒子滤波（particle filter，PF）算法［12］；②基于批处理的TBD算法，如最大似然概率数据互联（maximum likelihood-probabilistic data association，ML-PDA）算法［3］、最大似然-概率多假设跟踪（maximum likelihood-probabilistic multiple hypothesis tracking，MLPMHT）算法［4］等。由于使用了原始数据或门限很低的观测数据，TBD算法的计算量通常远大于TAD算法。

ML-PDA通过多帧累积的方式获得检测和跟踪高密度杂波环境中极低可观测目标的能力［5］。它基于多帧观测数据构建被跟踪目标状态向量的对数似然比（log likelihood ratio，LLR）。以LLR最大化时所对应的目标状态向量作为被跟踪目标在起始帧时刻的状态估计。目标的LLR搜索面具有很多局部峰值。实现该最大化寻优有3种常用方法［6］：多遍网格（multi-pass grid，MPG）搜索法，基于遗传算法（genetic algorithm，GA）的优化方法和直接子空间搜索（directed subspace search，DSS）法。其中，MPG搜索方法基于梯度优化。若起始点选取不当，该方法容易收敛于局部而非全局最优值；第二种优化方法中，首先使用GA算法将目标状态“粗调”至全局最优附近，再通过梯度收敛方法进一步“细调”到全局最优。该方法的优化性能良好，主要问题是迭代次数多，对较高的收敛精度需要较多的种子数，以至于影响实时性。DSS算法将观测值反映射回参数空间，作为起始点进行搜索。该方法有较快的收敛速度。然而，其使用的前提是量测空间为参数空间的子空间。这要求应用场景中观测值能够被反映射回参数空间［6］。但很多应用中（如基于角度多普勒的目标跟踪等），该条件并不满足。总之，计算量大依然是限制ML-PDA工程应用的主要因素。

图形处理器（graphic processing unit，GPU）能够并发执行数万个线程。它为通用算法的并行化提供了一个有效的实现平台［7］。近年来，GPU已成为处理高计算复杂度的目标检测与跟踪算法的流行工具［89］。

为解决ML-PDA的计算量问题，本文提出基于观测引导粒子群优化（particle swarm optimization，PSO）的MLPDA算法及其GPU实现。相比于GA，PSO每次迭代的步骤少，且不涉及数据间的进制转换问题，收敛效率更高［10］；基于观测引导PSO步骤，提高PSO的收敛效率；基于GPU的算法并行实现，满足了ML-PDA的工程实时性需求。

本文章节安排如下：第1节介绍ML-PDA算法中LLR的构建以及已有的LLR优化算法；第2节介绍PSO优化及其用于ML-PDA中的策略；第3节介绍基于GPU的并行计算，以及基于PSO优化算法的ML-PDA的并行实现策略。本文所提方法的计算效率将在第4节中通过仿真验证。第5节进行工作总结并展望后续研究。

1 ML-PDA算法

ML-PDA是一种批处理TBD算法。它使用最近的Nw帧数据估计目标的状态向量。当新数据到来后，将采用滑窗方式移出前Nw帧数据的第一帧，并将最新一帧数据作为滑窗中的第Nw帧。ML-PDA算法遵循如下基本假设：

假设1已知目标的检测概率为Pd，且目标的检测在帧间是独立进行的；

假设2每帧数据中至多有一个量测来源于目标；

假设3已知目标状态的变化方式；

假设4监测区域的体积为U，杂波在监测区域内呈均匀分布；

假设5监测区域内的杂波数呈泊松分布，且已知该分布的密度为λ，概率强度方程为μf（m），观测数据的虚警概率为Pfa；

假设6目标回波幅度的服从p1（a）的分布，杂波幅度服从p0（a）的分布，且监测区域的SNR已知或能够被实时估计；

假设7目标量测被加性高斯白噪声干扰；

假设8每帧数据中目标产生的量测彼此独立。

在ML-PDA算法中，假设待估计目标的参数为xr，且运动模型F已知，则目标在第i帧的运动状态可由式（1）得到：

目标的量测集由式（2）得到：

式中，i＝1，2，…，Nw表示目标观测数据的帧数；j＝1，2，…，mi表示对应数据帧内的量测个数；zij表示目标运动有关的观测数据；aij表示对应量测的幅度。令观测站在获取第i帧量测时所处的位置为xs（i），则量测z与xr，xs（i）间的关系可由式（3）给出。

式中，H（·）为观测方程；wi表示零均值且协方差矩阵为R的高斯白噪声。则LLR可由式（4）～式（6）表示。

式中，ρij表示幅度似然比；τ表示检测算法所设置的门限；p1（aij｜τ）表示目标存在的假设；p0（aij｜τ）表示目标不存在的假设；N（·）表示高斯分布。

至此，待估计的目标参数可由式（7）给出。

式中，t表示目标参数xr的采样时刻。

早期的ML-PDA中普遍使用MPG算法来求取^x（t）。文献［6］证明，GA搜索与DSS方法能够获得更高的搜索效率与估计精度。然而，GA算法的精度与播撒种子的数量成正比，不利于算法的实时实现；DSS方法的使用条件则在一些实际应用中无法得到满足。此外，文献［10］证明，在相同条件下，PSO的搜索效率要高于GA。

2 观测引导PSO的ML-PDA算法

2.1 基于PSO优化LLR

PSO是一种优化算法。给定目标方程f（y），其中y代表被搜索向量的参数，Np个粒子被播撒在参数空间中。每个粒子在搜索时，将会考虑到各自的搜索历史最好点和群体内其他粒子的历史最好点，并在此基础上变化位置。群中的第n个粒子由3个向量组成：当前位置yn、历史最优位置pn以及速度vn。yn被看作描述空间点的一套坐标。在算法迭代中，yn作为问题解被f（yn）评价。整个粒子群中迄今为止搜索到的最好位置表示为pg。

在一次迭代中，对于粒子n，其第d维基于式（8）和式（9）变化。

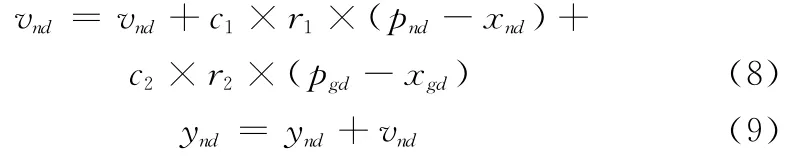
式中，c1，c2是两个非负值，代表移动常数，它们使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点以及群体内的全局最优点靠近；r1，r2是在［0，1］中取值的随机函数；为限制粒子单次移动距离，设移动距离上限［Vmax］d：若vnd＜－［Vmax］d，则令vnd＝－［Vmax］d，反之，若vnd＞［Vmax］d，则令vnd＝［Vmax］d。基于PSO优化ML-PDA的LLR流程如下：

步骤2评价粒子：对每一个粒子，通过LLR公式Λ（Z，a｜xn）评价其适应指数。

步骤3按照式（8）和式（9）改变粒子的速度和位置。

步骤4更新最优：比较粒子适应指数与其个体最优值，若优于个体最优，则将个体最优更新为当前粒子位置；比较粒子适用值与全局最优值，若优于全局最优，则将全局最优值更新为当前粒子位置。

步骤5停止条件：若满足收敛条件，则停止；若不满足，则返回步骤2。

2.2 基于观测引导的PSO优化算法

在文献［6］提出的两种算法中，GA在参数空间里随机撒种，而DSS要求参数空间与观测空间一一对应。前者虽然有一定的收敛效率，但在对目标位置没有任何先验信息的环境中随机撒种，收敛效率将会很低。究其原因，在LLR表面，局部最优值相关的部分只占约30%［11］，即有约0.7× Np数量的种子被撒在LLR底部，起不到任何作用。然而，若目标在第一帧观测数据中未被检测，通过随机撒种将有更大的可能性将其检出。基于以上考虑，本文提出在充分考虑LLR以及观测数据的特性基础上，由观测引导撒种来进一步提升PSO的收敛效率，从而在算法层面多普勒减少计算时间。如图1（b）所示，使用角度多普勒作引导，PSO的撒种变得有针对性。如图1（c）所示，若加上距离观测信息作引导，进入目标高似然区域的粒子进一步增加，可以更少的迭代次数完成优化。

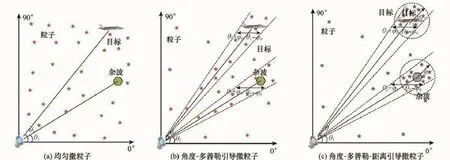
图1 基于观测引导PSO播撒粒子示意图

观测引导的PSO优化步骤如下：

步骤1初始化：接收第一帧观测数据，假设一共接收到m1个量测；

步骤2假设为每个量测分配的种子数为Ns，角度观测标准差为φθ，则在以每个量测为中心，加减φθ的范围内均匀播撒Ns个种子。此外，为捕获第一帧量测可能的目标漏检，额外播撒Nd个种子，则共产生Nd＋Ns×m1个种子。

步骤3～步骤6参照第2.1节基于PSO优化ML-PDA的LLR算法步骤2～步骤5。

3 基于GPU实现观测引导PSO的ML-PDA

在优化过程中，LLR被作为优化算法的评价函数。由于构建LLR会用到多帧观测数据，并且粒子的维度较高，因此评价单个粒子的适应程度会耗费一定的时间。此外，为达到较高的搜索精度，播撒的种子数一般较大，需要的迭代次数也多。ML-PDA算法的实时性难以保证。本节将PSO算法特点与ML-PDA结合起来，提出基于GPU平台的ML-PDA实现策略，使ML-PDA得以实时实施。

3.1 GPU简介

GPU拥有一簇流多处理器，每个SM内有多个流处理器。它们能够被用于并行执行计算任务。CUDA（computer unified device architecture）是一个通用计算框架。它能够高效地协调GPU和CPU共同处理复杂的计算任务。在CUDA中，CPU被认为是Host，GPU被认为是Device。其中，Host一般用于执行串行任务以及初始化GPU核函数，而GPU则用于执行高度并行化的计算任务。GPU核函数一般可启用上万个并发线程，这些线程分为两个层次：网格以及块。同一个块内的线程可通过共享存储器交互数据，不同块内的线程可通过全局存储器交互数据。一般来说，共享存储器的访问速度远高于全局存储器。CUDA的结构如图2所示。其中，Gdx，Gdy，Bdx，Bdy分别表示网格内每行、列分配的最多块数量，以及每个块内行、列分配的最多线程数。这4个参数在初始化核函数时被指定。

3.2 基于观测引导PSO的ML-PDA算法在GPU上的实现

考虑到需要存储的数据较多，本文将粒子的位置、速度信息以及接收到的观测数据等存储在全局存储器中。由于全局存储器是按一维存储数据的，本文基于文献［12］的数据存储形式，将算法中所有的二维矩阵数据映射成一维向量，方便GPU存取。

图2 CUDA结构图

PSO算法在撒种以及粒子迁移时需要使用随机数。现有的GPU实现PSO算法的文献［12- 13］中采用空间换取时间的策略：在CPU端生成大量随机数，并预先传入GPU。然而，在ML-PDA算法中，观测数据较多，并需要较多的高维度种子，对存储的需求非常大，以至于上述策略不再有效。因此，本文采用在GPU端生成随机数的方法［14］。

此外，在PSO算法中需要更新全局最优种子。全局的历史最优值被动态更新需要引入遍历过程。在CPU中执行此步骤时通过循环完成。遍历Nd＋Ns×m1个元素需用到Nd＋Ns×m1－1次循环，并在归一化的时候也需要用到Nd＋Ns×m1－1求和。而在GPU中，由于多个线程并行工作，将有Nd＋Ns×m1个线程同时访问全局最优值。若同时做更改操作，会产生冲突。因此，本文首先将全局最优值复制Nd＋Ns×m1次，每个线程更新其中一个全局最优值。待所有线程更新完后再选出其中的最大值，作为新的全局最优估计值。实现中，引入并行前缀求和（parallel prefix sum，PPS）［15］，使循环次数降至log2（Nd＋Ns×m1－1）次。PPS的实施如图3所示（以8个元素求和为例）。

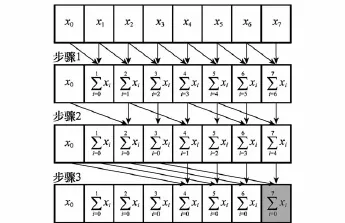
图3 PPS求和示意图

同样地，在求取最终状态时（需要求得所有种子参数的平均值），也通过多次运用PPS减少计算时间。

基于GPU实现观测引导PSO的ML-PDA算法流程如图4所示。

4 实验与仿真

4.1 仿真的硬件以及软件环境

仿真软硬件平台如表1所示。

图4 GPU实现观测引导PSO的ML-PDA算法流程图

表1 仿真软硬件平台

4.2 仿真场景

考虑一个基于主动声呐的水下运动目标探测场景［3］。目标的状态向量为［x，y，˙x，˙y］，其中（x，y）与（˙x，˙y）分别代表目标的二维空间位置与速度（笛卡尔坐标下）。该声呐可观测到目标与声呐位置的角度、距离和多普勒频率。其观测方程按式（10）给出。

式中，c为声波在水中的传播速度；γ为声呐信号的发射频率；γz为经目标反射后带多普勒信息的信号频率，传感器接收信号的频率范围Uγ＝［296 Hz，300 Hz］，角度观测范围Uθ＝［0°，50°］，距离观测范围Ur＝［12 700 m，14 200 m］。假设目标检测概率为Pd＝0.8，量测标准差分别为σγ＝0.01 Hz，σθ＝1°，σr＝100 m。采样间隔为10 s，共采集15个周期。令Nw＝10，目标真实的初始状态为［10 000 m，10 000 m／s，－5 m，－1 m／s］，声呐发射的信号频率γ＝300 Hz。设监视区域内的SNR为8 dB。观测空间中的杂波数期望值NFA与杂波密度λ关系如式（11）所示。

4.3 收敛速度对比

本节就所提出的优化算法与GA搜索算法进行对比。PSO算法及GA搜索算法参数设置如表2所示。分别令NFA＝10，20，40，独立仿真200次，并记录其收敛时的迭代次数。若搜索发散则记录算法迭代次数为100。各算法平均迭代次数如表3所示。由表3可知，在未加入观测信息时，使用PSO寻找最优解的循环次数要少于GA。但随着杂波密度的增加，算法需要更多的迭代次数来保证收敛到全局最优值。在加入观测引导之后，PSO撒种更有针对性，全局最优值出现更早，更有利于算法收敛。

表2 算法参数设置

表3 算法收敛效率对比

4.4 计算对比

本节分别使用GPU及CPU进行仿真，进一步验证3.2节提出的PSO并行化策略。令Ns＝15，Nd＝20，当NFA＝5时，在200次独立实验的情况下统计出计算精度

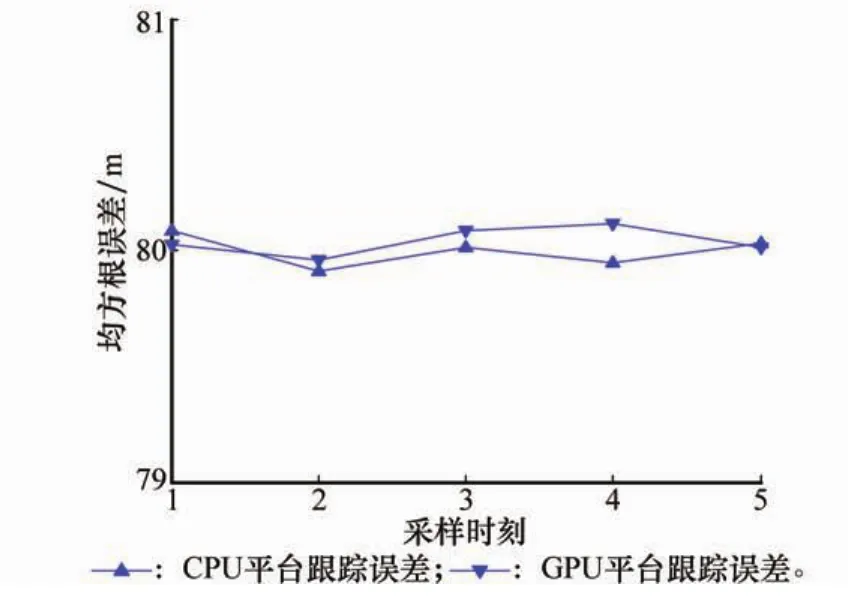
图5 CPU与GPU平台下计算精度对比

图6 CPU与GPU平台下计算时间对比

由图5可知，本文提出的并行化策略中，跟踪精度与CPU平台一致，但计算速度明显提升。随着种子数量增加，本文提出的GPU并行化策略的计算时间只少量增加。这是因为在GPU中只需增加一定数量的（并行）线程。即是说，无论种子数有多少，只要在GPU硬件限制的线程数（普通的GPU平台中可达数万个）内，均只需一次循环即可完成。略上升的计算时间来自种子数增加后所需数据拷贝时间的增加。如图6所示，在本仿真场景中，若平均杂波数如图5所示。改变NFA＝5，10，15，20，25（对应平均粒子数分别为：95，170，245，320，375），算法迭代限定16次。在500次平均的情况下，每次迭代执行时间以及加速比如图6所示。为25，所提出的方法在GPU平台上获得相比于CPU平台接近290倍的加速比。而从绝对计算时间看，该方法的单次迭代执行时间未超过1 s，远小于采样时间间隔，能够满足实时应用需求。

5 结论

本文针对低信噪比、密集杂波条件下的目标检测与跟踪问题，提出了以观测引导PSO的ML-PDA算法。并从工程应用的实时性角度考虑，提出基于GPU平台的ML-PDA算法实现。经仿真实验，该算法的搜索效率高于基于GA的ML-PDA算法。所提出的并行实现获得显著的加速比，且具有实时性。下一步的工作将着重扩展其在多目标跟踪场景［16］中的应用。

［1］Salmond D，Birch H.A particle filter for track-before-detect［C］∥Proc.of the American Control Conference，2001：3755- 3760.

［2］Boers Y，Driessen J.Particle filter based detection for tracking［C］∥Proc.of the American Control Conference，2001：4393- 4397.

［3］Kirubarajan T，Bar-Shalom Y.Low observable target motion analysis using amplitude information［J］.IEEE Trans.on Aerospace and Electronic Systems，1996，32（4）：1367- 1384.

［4］Streit R L，Luginbuhl T E.Maximum likelihood method for probabilistic multihypothesis tracking［C］∥Proc.of the SPIE International Symposium on Optical Engineering and Photonics in Aerospace Sensing，1994：394- 405.

［5］Schoenecker S，Willett P，Bar-Shalom Y.Comparing multitarget multisensor ML-PMHT with ML-PDA for VLO targets［C］∥Proc. of the 16th International Conference on Information Fusion，2013：250- 257.

［6］Blanding W R，Willett P，Bar-Shalom Y，et al.Directed subspace search ML-PDA with application to active sonar tracking［J］.IEEE Trans.on Aerospace and Electronic Systems，2008，44（1）：201- 206.

［7］Sanders J，Kandrot E.CUDA by example：an introduction to general-purpose GPU programming［M］.Boston，MA：Addison-Wesley，2010.

［8］Tang X，Su J Z，Zhao F B，et al.Particle filter track-before-detect implementation on GPU［J］.EURASIP Journal on Wireless Communications and Networking，2013，2013（1）：1- 9.

［9］Goodrum M A，Trotter M J，Aksel A，et al.Parallelization of particle filter algorithms［J］.Computer Architecture，2010，6161：139- 149.

［10］Shen Y，Guo B，Gu T X.Particle swarm optimization algorithm and comparison with genetic algorithm［J］.Journal of University of Electronic Science and Technology of China，2005，34（5）：696-699.（沈艳，郭兵，古天祥.粒子群优化算法及其与遗传算法的比较［J］.电子科技大学学报，2006，34（5）：696- 699.）

［11］Blanding W R，Willett P K，Bar-Shalom Y.Offline and realtime methods for ML-PDA track validation［J］.IEEE Trans. on Signal Processing，2007，55（5）：1994- 2006.

［12］Zhou Y，Tan Y.GPU-based parallel particle swarm optimization［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2009：1493- 1500.

［13］Mussi L，Daolio F，Cagnoni S.Evaluation of parallel particle swarm optimization algorithms within the CUDATMarchitecture［J］.Information Sciences，2011，181（20）：4642- 4657.

［14］Langdon W B.A fast high quality pseudo random number generator for n Vidia CUDA［C］∥Proc.of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference，2009：2511- 2513.

［15］Newcombe R A，Izadi S，Hilliges O，et al.KinectFusion：realtime dense surface mapping and tracking［C］∥Proc.of the 10th IEEE International Symposium on Mixed and Augmented Reality（ISMAR），2011：127- 136.

［16］Blanding W R，Willett P K，Bar-Shalom Y.ML-PDA：advances and a new multitarget approach［J］.EURASIP Journal on Advances in Signal Processing，2008：38- 56.

PSO based ML-PDA and its parallelized implementation

GAO Lin，TANG Xu，WEI Ping
（School of Electronics Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

The target detection and tracking problems when involved in high dense clutter are addressed.Specifically，we propose to solve the optimization and computation problems of maximum likelihood-probabilistic data association（ML-PDA）.The particle swarm optimization（PSO）algorithm to maximize the log likelihood ratio（LLR）is adopted.We propose to initialize the particles of PSO based on measurements，which improves the computation efficiency.Furthermore，we propose a scheme which allows implementing PSO in parallel on graphic processing unit（GPU）.The efficiency of the proposed algorithm and the parallelized scheme are illustrated based on simulations.

track before detect；maximum likelihood-probabilistic data association（ML-PDA）；particle swarm optimization（PSO）；parallel processing

TN 953

10.3969／j.issn.1001-506X.2015.12.02

高林（199-0-- ），男，博士研究生，主要研究方向为目标跟踪与信息融合。

E-mail：gaolin_uestc＠126.com

唐续（1975-- ），通讯作者，男，副教授，博士，主要研究方向为目标跟踪与信息融合。

E-mail：tangxu＠uestc.edu.cn

魏平（196-4-- ），男，教授，博士，主要研究方向为自适应阵列信号处理、非合作信号处理。

E-mail：pwei＠uestc.edu.cn

1001-506X（2015）12-2677-06

2014- 12- 21；

2015- 05- 27；网络优先出版日期：2015- 07- 27。