采用双轴加速度计的旋转弹运动姿态角速率测量方法

路永乐，潘英俊，黎蕾蕾，刘 宇，彭 慧

（1. 重庆大学光电技术及系统教育部重点实验室，重庆 400044；2. 武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079；3. 光电信息感测与传感技术重庆市重点实验室，重庆 400065；4. 中国电子科技集团公司第二十六研究所，重庆 400060）

采用双轴加速度计的旋转弹运动姿态角速率测量方法

路永乐1，潘英俊1，黎蕾蕾2，刘 宇3，彭 慧4

（1. 重庆大学光电技术及系统教育部重点实验室，重庆 400044；2. 武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079；3. 光电信息感测与传感技术重庆市重点实验室，重庆 400065；4. 中国电子科技集团公司第二十六研究所，重庆 400060）

研究了基于哥氏加速度原理的双轴加速度计测量旋转弹航向角角速率与俯仰角角速率的方法。首先根据哥氏加速度原理建立了旋转弹三维动力学模型，得出三个轴向加速度输出值同各轴角速率输入值之间的转换矩。针对旋转弹横滚角角速率远大于航向角角速率与俯仰角角速率的情况，建立了旋转弹的简化动力学模型；基于简化模型，提出了采用双轴正交加速度计测量横轴与竖轴上的加速度值，来实现对运动过程中航向角角速率与俯仰角角速率测量的方法。应用100 mm高射炮数据对该模型进行验证，验证结果同理论推导结果完全吻合。证明基于哥氏加速度的正交双轴加速度计测量旋转弹航向角角速率与俯仰角角速率理论的正确性和工程实现的可行性。

哥氏加速度；旋转弹；俯仰角；航向角

随着现代战争向着信息化、局部化方向发展以来，弹药的智能精准控制成为了一个重要的研究方向[1]。旋转弹通过自身旋转产生陀螺力矩以克服由推力偏心、质量偏心、气动偏心等引起的弹道散布，具有较强的抗干扰能力[2]受到了科研人员的青睐。由于高速旋转弹从出膛、飞行、侵彻等过程需要经历高冲击[3]、高动态[4]等极其恶劣极端的物理过程使得实时准确监测并控制旋转弹的运动姿态成为一大难题。

目前，测量旋转弹运动姿态角速率的方法大体可以分为：①天文导航法：包含太阳方位角遥测法、星敏器法，该方法受限于时间和天气因素[4-6]；②外界辅助导航法：包含GPS[7]、基于光电测量的外测法[8-9]，该方法很大程度依赖于外界辅助设备；③自主导航法：包含陀螺仪法[10]、地磁传感器法[3]、加速度计法[11-14]。自主导航方法可以不依赖外界设备，可以完全自主、实时准确地获得弹体的姿态信息。地磁传感器法具有自主导航优点的同时，且误差不随时间积累，但地磁传感器法要求不受磁性物质的干扰，在实战中很难满足。陀螺仪法在自主导航中有着大量的应用，但是光学陀螺仪、机械类陀螺仪难以承受旋转弹在出膛、侵彻等过程中高冲击的影响。振梁式陀螺仪[15-16]、MEMS陀螺仪具有抗冲击的潜能，但是由于旋转弹的高速自旋（1800 rad/s）将产生大的轴间干扰。传统的加速度计法有三加速度计法[11]、六加速度计法[12]、九加速度计法[13]、十二加速度计法[14]，这些方法同等条件下，体积大，成本高。

鉴于弹体体积小，三个轴向角速率、动态参数相差甚远的情况，本文提出了一种正交双轴加速度计测量旋转弹航向角角速率、俯仰角角速率的新方法。该方法将加速度计敏感方向分别沿横轴、竖轴方向放置，在避免纵轴方向高冲击的影响同时实现对横轴、竖轴方向上加速度的测量，进而实现全程、实时、无辐射、高采样的航向角角速率与俯仰角角速率检测。

1 正交双轴加速度计俯仰角角速率与航向角角速率测量原理

1.1 旋转弹原理

传统弹丸在飞行过程中，当所受合外力不通过质心时，合外力将导致弹丸翻转[17]。在来复线的作用下弹丸将高速自旋产生进动使弹丸具有轴向稳定性，在一定程度上消除空气阻力等外力的影响，进而增加系统瞄准和直射距离。旋转弹丸在弹道阶段自旋角速度是衰减的，目前能够较好地表述角速率和时间关系的为E.Roggla公式：

式中：ωg为弹丸膛口处自旋角速率(rad/s)，k为修正系数，L为弹丸长度(m)，D为弹丸直径(m)，ω为实时自旋角速率(rad/s)，A为弹丸转动惯量(kg·m2)。

王雨时根据实际测试结果得出E.Roggla公式的改写公式[18]：

角加速度与时间的半经验公式：

1.2 质点在直角坐标系中运动方程

如图1所示，质点在直角坐标系下位置表示为：

角动量矢量表示为：

质点的速度和加速度为：

式中：dr/dt为质点在惯性坐标系下的速度；∂r/∂t、∂2r/∂2t 为质点在转动坐标系下的速度和加速度；ω×r为转动坐标系相对惯性坐标系转动而产生的牵连速度；∂ω/∂t×r、ω×(ω×r)为因转动坐标系转动而产生的牵连切线加速度和向心加速度；2ω×∂r/∂t 为哥氏加速度,其与质点在转动坐标系下的相对速度∂r/∂t及转动坐标系的角速度ω有关。质点在转动坐标系中的位置r发生改变，使得质点的牵连切线速度ω×r亦随时间而改变，进而产生了加速度ω×∂r/∂t ;转动坐标系的转动改变了相对速度∂r/∂t的方向，将产生加速度为ω×∂r/∂t ，所以质点的哥氏加速度为2ω×∂r/∂t 。

如果质点的质量是m，作用在质点上的合力为F，则质点的运动方程为：

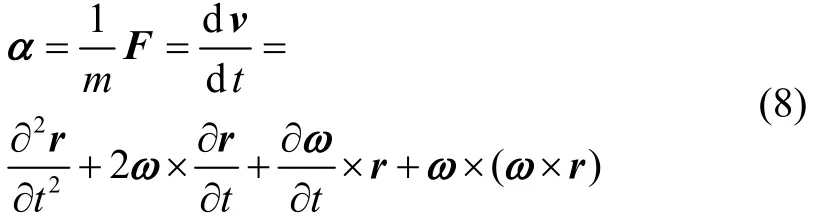
质点的三维运动方程用矩阵形式表述如下：

图 1 旋转弹在直角坐标系下的坐标定义Fig.1 Definition of projectile in rectangular coordinate system

2 正交双轴加速度计数学模型

旋转弹在飞行过程中航向角角速率ωz、俯仰角角速率ωy将远远小于横滚角角速率ωx，即ωx≫ωz，ωx≫ωy。由于旋转弹的小尺寸，纵轴轴向的高动态、高冲击，横轴轴向、竖轴轴向的低动态、小冲击的特殊环境，使得：根据公式(9)可得纵轴轴向加速度为：

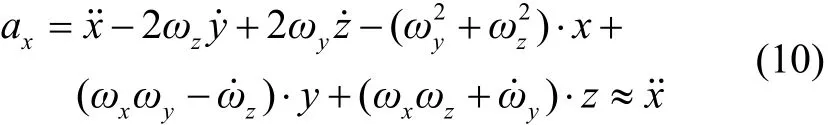
横轴轴向加速度为：

竖轴轴向加速度为：

把式(2)(3)带入式(11)(12)得：

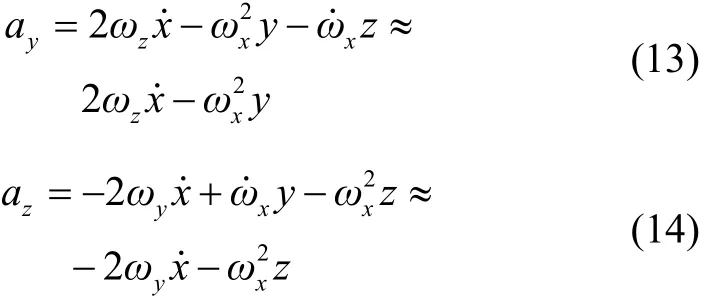
根据式(13)(14)可以看出，在旋转弹纵轴轴向速度已知情况下，通过测定横轴轴向、竖轴轴向加速度值，即可计算得到旋转弹航向角角速率、俯仰角角速率：

在现实环境中，重力场在横轴、纵轴上将产生一个频率为ωx/2π的正弦信号，横轴、纵轴输出信号相位相差90°。由于该信号属于已知频率的交流信号，通过带阻滤波器即可消除。

3 数据验证

采用100 mm高射炮测试数据进行离线Matlab仿真验证模型。根据文献[18]报道100 mm高射炮测试出膛角速率ωx=1 800 rad/s，飞行速度V=900 m/s。设定俯仰角角速率ωy=0.01 rad/s，航向角角速率ωz=0 rad/s，加速度计距离中心轴距离分别为0.04 m、0.04 m。

飞行过程中旋转弹自转角速率如图2所示，旋转弹的横滚角角速率随时间呈指数衰减。该过程横轴轴向加速度计，竖轴轴向加速度计输出值如图3所示，图中蓝线代表横轴轴向加速度输出值，红线代表竖轴轴向加速度计输出值。横轴和竖轴加速度计输出数值整体呈指数衰减规律，输出值中存在向心加速度分量，向心加速度在旋转弹飞行过程中只与自转角速度相关。将横轴和竖轴加速度计输出值与时间关系进行数值拟合，拟合形式为y=b•exp(a•t)，置信区间设为95%，拟合结果如表1所示。表1显示，横轴轴向加速度计输出值与时间呈现指数衰减关系其衰减系数-0.0212，为横滚角角速率衰减系数-0.0106的2倍，同理论值完全吻合；竖轴轴向加速度计输出值与横轴轴向加速度计输出值呈同样的规律。进一步分析横轴与竖轴轴向加速度计输出值同横滚角角速率的相关性，结果如表1所示，横轴与竖轴轴向加速度计输出值同横滚角角速率相关系数同为-0.9999，由此可得，横轴与竖轴轴向加速度计输出值同横滚角角速率高度相关。

图4为横轴与竖轴轴向加速度计输出值经过向心加速度补偿后的数值，理论上横轴轴向加速值输出为零，竖轴轴向加速度值输出为-18 m/s2，而从图4中可以看出，仅仅经过向心加速度值修正后的输出值同理想值之间存在一定误差。该误差随时间推移逐渐减小，误差最大值0.7659 m/s2出现在开机启动时。

表1 加速度计原始输出数据拟合及相关性分析表Tab.1 Results of original data fitting and correlation

通过式(9)旋转弹三维动力学模型可知，横轴轴向加速度计输出值中包含向心加速度误差、航向角角速率干扰、横滚角角速率干扰，而后两者统称为轴间干扰。竖轴轴向加速度计输出值同样存在向心加速度误差、轴间干扰误差。因此图4中所示误差为轴间干扰误差所致。

由于横滚角角速率远远大于其他两个轴向的输入，因此在旋转弹飞行过程中轴间干扰误差主要由横滚角角速率产生。采用指数函数y=b•exp(a•t)对轴间干扰误差同时间的关系进行拟合，结果如表 所示。更一步验证轴间干扰误差同横滚角角速率、俯仰角角速率、航向角角速率的关系，分别求得轴间干扰误差同横滚角角速率、俯仰角角速率、航向角角速率的相关系数如表2所示。从表2可得，轴间干扰误差随时间的衰减系数-0.0212，轴间干扰误差与横滚角角速率相关系数为0.9999呈高度相关，与俯仰角角速率、航向角角速率无关。

基于此将数据带入(13)(14)的简化模型，将简化模型竖轴输出同加速度计输出进行对比，结果对比如图5所示。简化模型输出值同加速度计输出值重合，说明在俯仰角角速率、航向角角速率远小于旋转弹横滚角角速率的情况下，忽略俯仰角角速率和航向角角速率的影响是合理的。

表 2 加速度计误差数据拟合及相关性分析表Tab.2 Results of original data fitting and correlation

图2 自旋角速度同时间关系图Fig.2 Roll angle vs. time

图3 双轴加速度计输出值Fig.3 Output of acceleration

图4 轴间干扰效果图Fig.4 Effect of interference among axes

图5 简化模型与加速度计输出值对比图Fig.5 Result of the simplified model vs. acceleration

图6 补偿后加速度计输出值Fig.6 Compensated result of acceleration

对加速度计输出值同时进行向心加速度误差和轴间干扰误差补偿，补偿结果如图6所示。经过补偿后的加速度计输出从本质上抑制向心加速度误差和轴间干扰误差的影响。最后通过式(15)(16)解算得俯仰角角速率ωy=0.01 rad/s，航向角角速率ωz=0 rad/s，同真实值吻合。

4 结 论

本文分析了旋转弹在惯性坐标系下的运动状态，建立了旋转弹的三维动力学模型，得出三个轴向加速度输出值同各轴角速率输入值之间的转换矩阵。根据横滚角角速率远大于航向角角速率与俯仰角角速率的情况，进一步简化得出了旋转弹的三维动力学简化模型。基于此，提出了采用双轴加速度计测量旋转弹航向角角速率与俯仰角角速率的方法。根据旋转弹三维动力学模型得出向心加速度和轴间干扰是影响测量精度的主要误差。针对向心加速度和轴间干扰的产生机理得出横滚角角速率是产生这两种误差的根源，通过加速度计输出值与横滚角角速率做相关性分析，数据显示：两种误差同横滚角角速率相关系数均为0.9999，属高度相关。根据两种误差同横滚角角速度的对应关系，建立了利用补偿后加速度计输出值进行旋转弹航向角与俯仰角角速率求解的算法模型，采用100 mm高射炮一个飞行过程中的数据进行验证，数据验证结果同初设值完全吻合，证明了理论模型的正确性和工程实现的可行性。

（References）：

[1] Sahu J, Heavey K R. Progress in simulations of unsteady projectile aerodynamics[C]//High Performance Computing Modernization Program Users Group Conference. Schaumburg, IL,USA, 2010: 123-132.

[2] 苗瑞生, 吴甲生. 旋转弹空气动力学[J].力学进展, 1987, 17(4): 479-487. Miao Rui-sheng, Wu Jia-sheng. Aerodynamics of spinning projectiles[J]. Advances in Mechanics, 1987, 17(4): 479-487.

[3] Grandvallet B, Zemouche A, Boutayeb M, et al. Real-time attitude-independent three-axis magnetometer calibration for spinning projectiles: a sliding window approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 255-264.

[4] Nobahari H, Asl H G, Abtahi S F, et al. A backpropagation approach to compensate velocity and position errors in an integrated inertial/celestial navigation system using unscented Kalman filter[J]. Journal of Aerospace Engineering, 2014, 228(10): 1702-1712.

[5] Ning X L, Huang P P, Fang J C, et al. A new celestial navigation method for spacecraft on a gravity assist trajectory[J]. Mathematical Problems in Engineering, 2013, 42(5): 138-152.

[6] 王 鹏, 张迎春. 一种基于加速度计和天文的卫星自主导航新方法[J]. 中国惯性技术学报, 2013, 21(4): 489-494. Wang Peng, Zhang Ying-chun. New method of satellite autonomous navigation based on accelerometer and celestial navigation[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 489-494.

[7] Munguia R. A GPS-aided inertial navigation system in direct configuration[J]. Journal of Applied Research and Technology, 2014, 12(4): 803- 814.

[8] 龙达峰, 刘俊, 张晓明, 等. 高速旋转弹飞行姿态磁测解算方法[J]. 弹道学报, 2013, 25(2): 69-73. Long Da-feng, Liu Jun, Zhang Xiao-ming, et al. Magnetic survey solution method for flying attitude of high speed rotating ammunition[J]. Journal of Ballistics, 2013, 25(2): 69-73.

[9] Zhang R Y, Wang Y Q, Wu T, et al. Radar reflected signal process of high spinning rate projectiles[C]//The Eighth International Conference on Electronic Measurement and Instruments. Xi'an, China, 2007: 3982-3985.

[10] Stancin S, Tomazic S. Time and computation efficient calibration of MEMS 3D accelerometers and gyroscopes [J]. Sensors, 2014, 14: 14885-14915.

[11] 范成叶, 李杰, 景增增, 等. 旋转弹用三轴加速度计安装位置误差标定补偿技术[J]. 传感技术学报, 2013, 26(10): 1352-1356. Fan Cheng-ye, Li Jie, Jing Zeng-zeng, et al. Calibration and compensation method on installation position error of tri-axis accelerometer units used in spinning projectiles[J]. Chinese Journal of Sensors and Actuators, 2013, 26(10): 1352-1356.

[12] Hung C Y, Lee S C. A calibration method for sixaccelerometer INS[J]. International Journal of Control, Automation and Systems, 2006, 4(5): 615-623.

[13] 周红进, 许江宁, 覃方君, 等. 一种新的基于加速度计的无陀螺捷联惯性导航系统设计与实现[J]. 仪器仪表学报, 2008, 29(7): 1499-1502. Zhou Hong-jin, Xu Jiang-ning, Qin Fang-jun, et al. Design and realization of novel gyro-free strap down inertial navigation system based on accelerometer[J]. Chinese Journal of Scientific Instrument, 2008, 29(7): 1499 - 1502.

[14] Park S, Hong S K. Angular rate estimation using a distributed set of accelerometers[J]. Sensors 2011, 11(11): 10444-10457.

[15] 刘宇, 路永乐, 曾燎燎, 等. 固态振梁角速率传感器的动力学特性与误差分析[J]. 机械工程学报, 2011, 47(4): 7-11. Liu Yu, Lu Yong-le, Zeng Liao-liao, et al. Analysis on dynamic characteristic and error of solid vibration beam rate sensor[J]. Journal of Mechanical Engineering, 2011, 47(4): 7-11.

[16] Liu Yu, Lu Yong-le, Du Xiao-peng, et al. Analysis of high shocking resistance of an improved node plane supporting vibration beam gyroscope[J]. International Journal of Digital Content Technology and its Applications, 2012, 6(9): 319-328.

[17] 关世玺, 张斐, 范国勇, 等. 弹丸外弹道运动学分析及模拟试验[J]. 弹箭与制导学报，2012, 2(4): 165-169. Guan Shi-xi, Zhang Fei, Fan Guo-yong, et al. The analysis and simulation experiment of projectile's exterior trajectory kinematics[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 2(4): 165-169.

[18] 王雨时. 旋转弹丸外弹道自转角速度衰减规律半经验公式[J]. 探测与控制学报, 2003, 25(1): 1-6. Wang Yu-shi. Half-experiential formulas for calculating decreasing angular velocity of projectile in trajectory[J]. Journal of Detection & Control, 2003, 25(1): 1-6.

Measurement method of projectile’s heading and pitching angle velocities based on biaxial accelerometer

LU Yong-le1, PAN Ying-Jun1, LI Lei-lei2, LIU Yu3, PENG Hui4
(1. Key Lab. of Opto-Electronic Technology & System, Ministry of Education, Chongqing University, Chongqing 400044, China; 2. State Key Lab. of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China; 3. Chongqing Municipal Level Key Laboratory of Photoelectronic Information Sensing and Transmitting Technology, Chongqing 400065, China; 4. 26th Institute of China Electronics Technology Group Corporation, Chongqing 400060, China)

A measurement method of projectile’s heading angle velocity and pithing angle velocity based on the orthogonal biaxial Coriolis acceleration is proposed. In this study, a three-dimension dynamic model of the projectile in the inertial space is established based on the Coriolis acceleration principle. The transition matrix from angular velocity along the three axes to the acceleration for the three axes is obtained. The simplified dynamic model of the projectile is given as the values of roll angle velocity which are much bigger than the angle velocity value of heading or pitching. Based on this principle, the value of the heading angel velocity or pitching angle velocity can be measured by calculating the accelerations of the pitching axis and heading axis. The numerical simulation results of 100 mm anti-aircraft agree with the theoretical deduction results. The proposed method provides an effective theoretical guidance for measuring the projectile’s heading and pitching angle velocities based on the accelerometer.

Coriolis acceleration; spinning projectile; pitching angle; heading angle

V324.2+3

A

1005-6734(2015)02-0160-05

10.13695/j.cnki.12-1222/o3.2015.02.005

2014-10-28；

2014-11-20

国家自然科学基金资助项目（51175535）；中国博士后科学基金（2012M521470）

路永乐（1985—），男，博士研究生，从事惯性传感器及系统研究，中国惯性技术学会会员。

联 系 人：黎蕾蕾（1981—），男，博士后。E-mail：lill@cqu.edu.cn