民国时期国人自编三角学教科书中“三角函数”变迁

刘冰楠，代 钦

（内蒙古师范大学 科学技术史研究院，内蒙古 呼和浩特 010022）

民国时期国人自编三角学教科书中“三角函数”变迁

刘冰楠，代 钦

（内蒙古师范大学 科学技术史研究院，内蒙古 呼和浩特 010022）

三角学教科书中的“三角函数”在民国时期的不同阶段，呈现不同的特点．通过对课程标准的要求、内容设置的变迁、名词术语的变化等方面进行梳理，能够对当时三角学教科书有一个清晰的了解并折射出民国时期中国数学教育的一个侧面．从三角函数的定义方式、图像、诱导公式等方面看，其内容不断减少，难度有所降低．

民国；三角学教科书；三角函数

民国时期是中国数学教育走向现代化的重要时期，是数学教科书摆脱中国传统教育理念，融合西方先进的教育思想方法，逐渐与世界接轨的重要阶段．通过对民国三角学教科书教学要求、内容变迁、定义方式和名词术语的考察，可以为今天数学课程和教科书研究者提供有益借鉴．

1 时代背景

20世纪10年代，三角学教科书采用自编者较多．根据倪尚达在1920年对当时中等学校使用的数学教科书情况进行的统计可知[1]，《共和国教科书平三角大要》在当时的使用范围最广，从1913年初版至1923年已再版18次．20世纪20年代出版的中学数学教科书，主要有商务印书馆的“新学制教科书”、“现代初级中学教科书”和中华书局的“新中学教科书”．当时各中学可自行选定教科书．刘正经编辑的《现代初中教科书三角术》很受欢迎，1923年初版，1930年第54版，1936年国难订正第31版．20世纪30年代出版的教科书除商务印书馆、中华书局仍占有主要地位外，还有开明书店、世界书局、正中书局等．种类齐全，内容丰富，达到中国清末至解放前数学书籍出版的鼎盛时期．1933年初版的《复兴初级中学教科书三角》再版次数极多，至1948年已再版150次．

“1946年以后，中学教科书由审定制改为国定制，采用国立编译馆教科用书组依照新修订课程标准修改、编写的统一国定课本．”[2]然而，大多数学校还是采用原来的教科书．例如，商务印书馆的“复兴教科书”，中华书局的“修正课程标准适用”数学教科书仍被使用．张鹏飞编的《初中三角》1936年初版，1947年再版26次．但该书1940年以后的版本，将书名改为“修正课程标准适用”《初中三角法》继续使用．审定本即教科书在出版之前，须将稿本呈交给教育部，教育部审查通过后方可出版使用．其中，《共和国教科书》、《现代初级中学教科书》及《复兴教科书》均为审定本教科书．而国定本即教育部命令所属的“国立编译馆”，按照中小学校的全部科目，编辑一整套教科书，通过“教育图书审查委员会”审定后出版发行．

三角函数是三角学的核心，故这里选取以下4种具有代表性的教科书：① 黄元吉编纂《共和国教科书平三角大要》，商务印书馆1913年12月初版（后称1913年本）；② 刘正经编辑《现代初中教科书三角术》，商务印书馆1929年1月第29版（后称1929年本）；③ 周元瑞、周元谷编著《复兴初级中学教科书三角》，商务印书馆1933年7月初版（后称1933年本）；④ 张鹏飞编《初中三角法》，中华书局1947年4月第26版（后称1947年本）．以这4本影响较大，使用范围较广的国人自编三角学教科书作为研究对象，考察三角函数的变迁．图1为4本教科书的书影．

图1 四本三角学教科书书影

2 对6个三角函数发展历史的简单回顾

公元前2世纪，西帕索斯首创三角学，直至16世纪之前，主要以天文学伴侣的姿态出现．由于航海、天文观测等实际问题的需要，使得球面三角术的出现比平面三角术早得多．1533年，德国数学家雷吉奥蒙塔努斯（J. Regiomontanus，1436—1476）出版《论三角形》（On Triangles of Every Kind），在欧洲这是第一本使三角学脱离天文学而正式成为数学的一个独立分支学科的标志性著作．1748年，欧拉在《无穷小分析引论》中引入了三角函数的概念，并将三角函数看作是一种函数线与圆半径的比．16世纪末期，西方传教士来中国传教，三角学作为西洋历法的数学基础传入中国．

约公元510年，阿里亚哈塔（Aryabhata，约公元475—550）所写的《阿耶波多历书》（Aryabhatiya）是第一本明确提出正弦函数的著作．伦敦Gresham学院的天文学教授冈特（Edmund Gunter，1581—1626）在1624年发明了一个用来计算对数的机械工具——冈特刻度，是人们现在所熟悉的计算尺的前身．而sin和tan这两个符号，就是在“冈特刻度”的图示说明中首次出现．1631年瑞士来华传教士邓玉函（Jean Terrenz，1576—1630）编《大测》一书时将sinus译为“正半弦”，简称为正弦，这就成了中国“正弦”一词的由来．由于要计算余角的正弦值而出现了余弦函数，单词cosinus（余弦）最初是冈特使用的，缩写符号cos则是在1674年，由英国数学家和测量员摩尔（Jonas Moore，1617—1679）爵士率先使用．正切和余切这两个比率源自日晷和投影的想法，把这两个比率作为角的函数是由阿拉伯人开始的．Tangent在1583年丹麦数学家芬克（Thomas Fincke，1561—1646）的著作《圆的几何》中首次出现．Cotangens在1620年被冈特首次使用．阿拉伯学者阿布—威法（Abul-Wefa，公元940—998）是第一个制作出正切函数表的学者，此函数表在15世纪航海表计算出来后大显身手．正割和余割这两个函数在阿布—威法的著作中第一次提到，但却没有给出具体的名称．sec这个符号是由法国数学家吉拉德（Albert Girard，1595—1632）首次提出．雷提库斯（Georg Joachim Rhaeticus，1514—1576）是哥白尼的第一个学生，他的著作《三角学说准则》（Canon Doctrinae Triangulorum，1551）中6个三角函数首次同时出现．

3 4种教科书中“三角函数”的比较

3.1 课程标准的要求比较

1912年9月，中华民国教育部公布了《中学校令》，将中学校修业年限定为4年，共14门课程．其中，中学校之学科目与其程度，及教科书之采用，别以规程定之．同年12月，颁布《中学校令施行规则》，其中第一章第七条规定：“数学要旨，在明数量之关系，熟习计算，并使其思虑精确．数学宜授以算术、代数、几何及三角法．女子中学校数学可减去三角法．”[3]1913年3月19日公布的《中学校课程标准》，将授课时数按照男女生进行修改，如表1所示[3]．

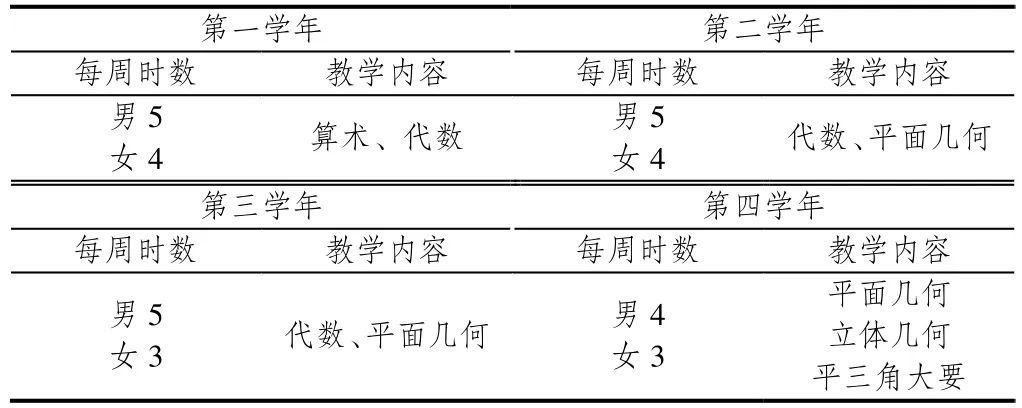
表1 1913年中学校课程标准数学科授课时数与教学内容

中华民国教育部于1923年制定了《新学制课程标准纲要》，其中《初级中学算学课程纲要》要求初中数学采用混合编排，并且规定三角部分的毕业最低限度为“略知平面三角初步”．“对于1923年的混编教材，由于有些学校不适应，在实施混合课程时仍用分科教材．”[4]1929年，南京政府大学院（10月改组为教育部）根据全国教育会议议决组成中小学课程标准起草委员会编订《初级中学算学暂行课程标准》，令各省作为暂行标准，试验推行．初中设14科目，共180学分，其中算学为30学分．三角在三年级下学期与几何同时教授，三角每周授课时数为3小时．

1936年颁布的《初级中学算学课程标准》是教育部根据各地反映“教学总时数之过多”，对1933年颁布的“课程标准”进行修正而成，其中规定：“三角之正式教授，宜移至高中，但三角应用方面极广，初中亦不可不知．故宜就实例入手，讲授三角函数定义，及直角三角形解法，简易测量，余可从略．”[3]

1941年的《修正初级中学数学课程标准》中取消了三角这门课程，三角仅在高中第一学年讲授，并在《修正高级中学数学课程标准》中有相关的要求，每周课时为2小时．

3.2 三角函数内容设置的比较

（1）三角函数内容的整体安排．

1913年本是辛亥革命胜利后，商务印书馆出版的第一套国人自编教科书．为了合乎于“共和民国”的宗旨，故取名为《共和国教科书》．这套教科书顺应世变，适合民国政体更新的需要，奠定了民国初年中小学新式教科书的基础[5]．1913年本共两篇十一章，55页．其中，三角函数占28页．主要内容有[6]：锐角之圆函数、普通角之圆函数．书中附有希腊文字对照表，包括希腊字母的大、小写写法及其名称，并用希腊字母表示角，如sinα、cosβ等．书中的定理、例题、习题等开始渗透分类的思想．

1929年本共八章，106页，三角函数占29页．主要内容有：三角术之目的、锐角之三角函数、直角三角形解法、对数及对数计算、普通三角形边角的关系、普通三角形解法、任何角的三角函数、几个重要的恒等式．在此引用该书“编辑大意”说明当时的编排情况[7]：

① 这本小书，是编给中等学校做教科书用的．中等学生对于三角术只要在实用方面够用，所以本书注重实用；至于理论方面，也不偏废，不过别为补篇．书名虽定为初中三角术，但是旧制中学第四年，也可采用，因为有补篇可以伸缩．

② 应用问题的选择，以能鼓起学生的兴味为标准．这里面大多数是从著名的教科书内摘译下来的，还有一部分是特别为这本书做的．

③ 书中常常插入关于三角术历史上的谈话——本国和外国两方面，都有一点——使学生知道三角术大概的沿革，并且可以引起他们研究的兴趣．

④ 后面所附的四位表，在本国算是很新的一种．他的排列得当，检查便利，很足以保证他的实用价值，用不着编者多说话．

⑤ 编者仅向南开大学算学教授姜立夫博士表示至诚的感谢，因为他费了很多的功夫，把这本书的稿子看过了，并且加以许多有价值的批评，尤其是关于历史方面的材料承他很费心的帮助搜集．又南开同事算学教员张芷宾先生，在搜集应用问题方面，很替编者帮忙，并且编辑中也得他的臂助不少，谨记于此，以至感谢．

1929年本后两章为补篇，具有一定的弹性，不但可供新制初中使用，也可供旧制四年级使用．其中，任意角的三角函数安排在补篇中，教师可根据实际情况进行讲授．书中常穿插国内外关于三角术的历史，使学生了解三角术的沿革，激发他们的学习兴趣．同时，增加了对数及对数计算一章．

1933年本共六章，有87页．三角函数占24页．主要内容有[8]：三角比、基本公式、三角函数及其应用、对数解法、任意三角形的解法、三角法的应用．书中的习题，为切合学生的生活状况，大多选择实际问题，与前几本教科书不同，1933年本除应用上必需的三角函数公式以外，其它一切的恒等式均被省略．对于内容的讲授，如果时间不足，第四章和第五章可酌情缩减，或将第六章完全省去．

1947年本共三编七章，有75页．其中三角函数占31页．主要内容有[9]：开端、锐角和三角函数的关系、直角三角形的解法和应用．整书中都没有用希腊字母表示角，而是用大写的英文字母表示．书中加入了变式习题，利于学生加深对问题的理解．

将4本三角学教科书中的内容进行分类量化，具体见表2．

表2 三角函数的内容

（2）三角函数概念引入方式的异同．

民国时期这4本教科书中三角函数定义都是直接给出的，之前没有做任何铺垫，都是在直角三角形中利用三角比进行定义的．并且仅给出6种三角函数，对于正矢和余矢两种函数没有提及．但4本教科书中6种三角函数给出的方式有所不同．对于三角函数的定义是以比率引入的，是在直角三角形中进行定义的，先限于直角三角形内的锐角，然后利用坐标，将定义推演于任意角，用以解决含有直角三角形的简单问题．

1913年本仅在直角三角形中定义了正弦和余弦，正切和余切是通过正弦和余弦的比值给出的，而正割和余割是利用正弦和余弦的倒数进行定义的．1929年本和1933年本基于正弦、余弦和正切3个函数使用较多的原因，在直角三角形中首先定义了这3个函数，而余切、正割和余割则作为前3个函数的倒数给出，因为只要知道了前3个，后3个的值就可以算出来．1947年本在直角三角形中定义了6种三角函数，并利用表格的形式给出了6个比例和相应的符号表示．从引入方式来讲，1929年本和1933年本突出强调了6个函数之间的关系，利于学生对三角函数的理解，不至混淆，方便后续三角函数关系的学习．

（3）三角函数图像和诱导公式的比较．

民国时期三角教科书大多将三角函数安排在第一章或第二章，内容较多，也是三角教科书的主要内容，所占课时较多．1913年本中的三角函数内容所占篇幅最多，例题和练习题的数量也最多，这样的安排在民国初期比较普遍．相比而言，周元瑞和周元谷编的教科书再版次数相当惊人，其受欢迎的程度可见一斑．

函数图像方面，这4本教科书都没有直接给出三角函数对应的函数图像．1913年本虽然没有直接给出三角函数的图像，却用表格的形式给出了3个函数（正弦、余弦、正切）在4个象限的符号．1929年本除了给出6个三角函数在各个象限的符号外，还给出了函数值在各个区间的变化情况，相当于已经给出了大致的函数图像，只是没有画出具体的图像而已．1933年本和1947年本对图像的相关问题没有提及．

1913年本和1929年本的诱导公式多而全，而1933年本和1947年本的内容明显缩减，除应用上必须的三角函数公式之外，其它恒等式都被省略．值得一提的是，在这4本教科书中，仅1947年本引入了三角比之六角形（如图2），用于记忆三角函数之间的关系，可看作是一种进步．

图2 三角比之六角形

三角比之六角形将三角函数按sin，cos，tan，cot，sec，csc的次序，每两项取水平位置，书写于六角形各顶点处，并将1标于六角形的中心．则有以下结论[9]：

（1）左右两侧，在下者之值较大，即大小关系为：sinA＜tanA ＜sec A 及cosA＜cotA＜cscA ；

（2）各对角线两端二函数之积，等于其中心数即1，是为二重关系．即

sinAcsc A=1，cosAsecA=1，tanAcotA=1；

（3）在相邻三角顶之三函数，其一端之函数，等于中间函数，以他端函数除之，是为三重关系．

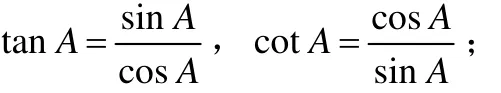
（4）同一水平线上相邻两函数之平方和，等于其下侧中央数之平方，是为平方关系．即：

sin2A+cos2A=1，1+tan2A =sec2A，1+cot2A =csc2A．

以上这8种关系均非各自独立，可由任意一平方关系，及其他任意四关系以求其余三关系．从记忆方面看，三角比之六角形具有一定的优势，但这个图形在现行教科书中已不出现．

（4）解决实际问题的比较．

生活是数学的源泉，数学与生活相互依存．这4本教科书的编写都较重视数学知识的应用，在直角三角形中利用三角函数解决生活中的实际问题．这种将数学问题与现实生活相联系、数学问题生活化的做法，不仅可以利用现实生活中的课程资源，开阔学生视野，同时也激发了学生学会应用数学的意识．如：

1913年本中虽然有实际应用问题，但正文内容均不是以实际问题为背景进行阐述的，而是将实际问题抽象出具体的图形，利用图形来表示，但在习题部分，却都是生活中的实例．主要有求塔高、求河宽、求房屋与街边的距离、求岩高、求山高、求云高、求二舰的距离等．

1929年本对应用问题内重要的术语进行了解释，如垂直线、垂直面、水平线、水平面视线、仰角、俯角等．具体有：求树高、求河宽、求行程问题、求山尖高、求墙高、求船距、求塔高等．

1933年本对在应用题上经常遇到的名词加以解释，尤其对仰角和俯角两个名词特别加以解释，除此之外还有垂直线、垂直面、水平线、水平面等．涉及的实际问题主要有：求树高、求屋子与树的距离、求竿长、求墙高、求两塔的距离、求街宽等．

1947年本的实际问题分为水平面内的简便测量和铅锤面的简便测量两类．主要涉及求河宽、求旗杆与山的距离、求墙高和墙宽、求树的高度等问题．

由表2可知，除1929年本，其他3本教科书的练习题中实际问题的数量较多，均十分重视三角函数对实际问题的应用．

3.3 三角函数的名词术语的演变

民国初期，采用算术、几何、三角的分科编排形式是这一时期教科书的编排特点之一．“《布利氏新式算学教科书》是20世纪中国翻译的第一套混合算学教科书．”[10]中国于1923年1月开始使用混合教科书，1929年后，在一部分学者的反对声中，教科书呈现两种形式，有的学校继续使用分科教科书，而有的学校则采用混合教科书，直至1941年彻底取消混合教科书．受其影响，三角函数的名词术语在混合教科书和分科教科书中略有不同．

如，民国时期的分科教科书中，将三角函数称为三角比例数、圆函数、三角倚数或三角比．清末时期把三角函数称之为三角比例数，如算学研究会编《平三角法教科书》（1906年）；1913年本中将三角函数称作圆函数．受外文原版书的影响，1923年汪桂荣起草的《高级中学第二组必修的三角课程纲要》中，将三角函数称之为三角倚数．1933年本将三角函数也称之为三角比．相比而言，民国时期的混合教科书中三角函数的名词术语不及分科教科书中的丰富，其中，将三角函数亦称作三角比，如布利士力著《布利氏新式算学教科书》（第三编）（王自芸译，商务印书馆，1922），程廷熙和傅种孙编《初级混合数学》（第三册）（中华书局，1923），段育华编《新学制混合算学教科书》（第四册）（商务印书馆，1925）．

根据段育华和周元瑞编的《算学辞典》，可对民国时期三角函数的定义有一个明确的认识：

“三角函数（Trigonometrical Function）超越函数之一种，亦称圆函数，又称三角比．若是者一角之正弦余弦正切余切正割余割，称为其角之三角函数．

三角比（Trigonometrical Ratio）即三角函数，因三角函数系由一角两边之比推得，故又名三角比．

与段育华和周元瑞编的《算学辞典》不同的是，倪德基、郦禄琦编《数学辞典》和赵缭编《数学辞典》中将三角函数又称之为八线．如：

“角之正弦，余弦，正切，余切，正割，余割，正矢，余矢，八者谓之角之三角函数，亦称三角比，或圆函数或八线．”[12]“角之正弦，余弦，正切，余切，正割，余割，谓之三角函数，又谓之圆函数．三角比同三角函数．八线旧译三角函数之名．谓正弦，余弦，正切，余切，正割，余割，正矢，余矢也．”[13]

三角比是随着角度的改变而改变的．当角度一定时，三角比就有一定的数值．如果角度改变，三角比也就相应地改变．那么照函数的定义说，三角比是角的函数，所以三角比又叫做三角函数．而称其为圆函数是符合三角函数的发展历史的．

4 结 语

通过上述比较，可以得出一些结论，民国时期三角教科书的编排特色也让研究者对当今教科书的编写产生了一些思考．

4.1 三角函数的内容减少且难度降低

从内容上来讲，1913年本的内容最少而且最为简单，概念、定理、公式等十分简洁、明了，例题、习题的数量适中，学生能够在规定的学业年限中从容毕业．1929年本从难度上来讲则略高一层，以表格的形式给出了6个三角函数在各个象限的符号及各区间的取值范围，较为全面地向学生呈现了三角函数的内容．1933年本的内容较1929年本大幅减少，其中诱导公式仅给出应用时必须的几个，而对于其它恒等式一概删去．而且内容的讲授可根据实际情况进行删减，具有一定的弹性，这也许是其受各学校欢迎的原因之一．1947年本比1913年本的内容略多，但诱导公式却从1913年的23个减少到3个．从整体难易程度上来讲，大致呈下降的趋势．1929年本和1933年本难度大于1913年本和1947年本．由于1913年本编写仓促，属于应急的教科书，所以相比其它3本教科书，内容最为简洁．1929年本间接地给出了三角函数图像，渗透了三角函数的周期性，涉及的三角函数知识最多，难度最大．

与民国时期初级中学三角教科书相比，中国现行初中数学教科书中没有讲授诱导公式，这部分内容被放在高中阶段进行学习．民国时期在初中就已经习得三角函数的诱导公式，从这方面来讲，民国时期所学内容要比现在的深，难度大．

4.2 内容安排次序的变化

民国时期三角学教科书中，关于“三角函数关系”和“直角三角形解法”这两部分内容的次序安排有两种不同的形式．在中国自编的三角学教科书中，大多将“三角函数关系”放在“直角三角形解法”之前．在当时翻译的日本教科书是按照先“三角函数关系”，再“直角三角形解法”的顺序安排，如远藤又藏著《平面三角法教科书》（葛祖兰译，文明书局，1914年）．而翻译欧美的三角学教科书则是按照先“直角三角形解法”后“三角函数关系”，如葛氏三角、温氏三角等．

汪桂荣在1923年起草的《三角课程纲要》中建议将“三角函数关系”放在“直角三角形解法”之后，“斜角三角形解法”放于“诸角三角函数”之前．这样的建议也许是受中国当时由学习日本转向学习欧美这样大环境的影响，或许是由于三角函数定义本身的呈现方式问题．但这些只不过是编排的问题，并不能由此说明哪种编排的好坏．至于中国自编的教科书为何没有采用欧美译本的编排方式，大概是基于日译本并不十分适合中国当时的教育以及课程标准中没有明确规定等原因，从这一点来说，民国时期数学教育的自由状态也可见一斑．

总之，教科书的编写要通俗易懂，平易近人，为大众服务，这对当前的数学教育改革也具有重要的现实意义[14]．三角学教科书从民国至今，在经历一个世纪的变迁后，数学知识逐步顺应时代的需要，发生了较大的变化．通过了解三角函数内容的变化，有利于厘清三角学教科书的发展脉络，管窥民国时期的教育理念．三角函数从注重函数、实用等问题逐步与其它学科相联系，如三角关系式与代数中的方程之间的关系，逐步实现各门学科的融合．回顾三角函数在民国时期的变迁历程，对中国目前数学教科书的编写具有重要的参考价值，并对当今的数学教育教学具有一定的借鉴意义．

[1] 倪尚达．全国中等学校数学科教授状况之调查[J]．教育杂志，1920，（5）：16 880-16 886．

[2] 吕世虎．20世纪中国中学数学课程的发展（1901—1949）[J]．数学通报，2007，（6）：9-13．

[3] 课程教材研究所．20世纪中国中小学课程标准·教学大纲汇编：数学卷[M]．北京：人民教育出版社，1999．

[4] 吕世虎，吴春燕，陈婷．20世纪以来中国中学数学课程内容综合化的历程及其启示[J]．数学教育学报，2009，18（6）：1-5．

[5] 李华兴．民国教育史[M]．上海：上海教育出版社，1997．

[6] 黄元吉．共和国教科书平三角大要[M]．上海：商务印书馆，1913．

[7] 刘正经．现代初中教科书三角术[M]．上海：商务印书馆，1929．

[8] 周元瑞，周元谷．复兴教科书三角[M]．上海：商务印书馆，1933．

[9] 张鹏飞．初中三角法[M]．上海：中华书局，1947．

[10] 陈婷，吕世虎．二十世纪混合数学教科书的先河——《布利氏新式算学教科书》之考察[J]．数学教育学报，2013，22（2）：84．

[11] 段育华，周元瑞．算学辞典[M]．上海：商务印书馆，1938．

[12] 倪德基，郦禄琦．数学辞典[M]．上海：中华书局，1925．

[13] 赵缭．数学辞典[M]．上海：群益书社，1923．

[14] 代钦，李春兰．中国数学教育史研究进展70年之回顾与反思[J]．数学教育学报，2007，16（3）：6-12．

Transition of Trigonometric Functions in the Trigonometry Textbooks Compiled by Our Compatriots during the Period of Republic of China

LIU Bing-nan, DAI Qin
(Institute for the History of Science and Technology, Inner Mongolia Normal University, Inner Mongolia Huhhot 010022, China)

In each period of the Republic of China, the trigonometric functions in trigonometry textbooks represent varial characteristics. Through sorting out the transition of the requirement of curriculum standards, contents and the usage of terms, we could get a vivid picture of trigonometry textbooks and something of mathematics education in Republic of China. In the textbook, the contents and difficulty had been reduced in the aspects of defination, image and formula of trigonometric functions.

the Republic of China; trigonometry textbooks; trigonometric functions

G40-055

：A

：1004–9894（2015）03–0081–05

[责任编校：周学智]

2015–01–21

内蒙古师范大学研究生科研创新基金资助项目（CXJJBZD13002）；2012年高等学校博士学科点专项科研基金联合资助课题——中国中学数学教科书整理研究（1902—1949）（20121502110001）

刘冰楠（1986—），女，黑龙江鹤岗人，博士研究生，主要从事数学史与数学教育研究．