运用关键性教学事件分析支撑中国式数学课例研究

杨玉东，王 兄

（1．上海市教育科学研究院，上海 200032；2．上海师范大学 数理学院，上海 200234）

运用关键性教学事件分析支撑中国式数学课例研究

杨玉东1，王 兄2

（1．上海市教育科学研究院，上海 200032；2．上海师范大学 数理学院，上海 200234）

教研制度是具有中国特色的教育体系中的一部分，数学教研组几乎存在于每一所学校．通过一个数学教研组活动的案例，揭示数学教师如何在3轮授课的教研活动中凭借经验有意识或无意识地运用基于“重点·难点·关键点”的关键性教学事件分析不断地“磨课”的过程．基于该数学教研组的案例，试图讨论这种通过集体合作研讨改进课堂教学的教研活动的特点，并期望教师们能够继承传统教研组活动中的精髓并更加有意识地应用到数学课例分析当中．

课例研究；教研活动；关键性教学事件分析；重点；难点；关键点

世界各地的教师均被要求通过专业发展活动来提高他们的课堂教学水平．在西方，也提出了许多促进教师专业水平的活动形式，如工作坊培训、同伴互助、教学案例研究等[1～3]．自从《教学的差距》一书中展示了日本、美国和德国的课堂教学案例以来，日本的课例研究已被广泛地借鉴[4]，许多国际教育学者在推广展类似日本的课例研究提升在职教师的课堂教学水平[5～6]．实际上在中国，一种非常类似于日本的课例研究活动——被称为“磨课”的教研组活动，自20世纪50年代以来就在进行，但很少被西方学者所知晓．

尽管中国的数学教师的学历水平远不及西方或日本同行，一些研究已表明中国的数学教师对初等数学有深刻理解，具有足够的数学学科教学知识并能把这类知识运用到日常教学中[7～9]．既然中国数学教师职前受到的专业训练相对不足，却在实践中具有优势，那么可能的原因就是他们得益于在校本环境中所开展的各类教研活动．下文将描述一个上海的数学教研组如何对于同一授课内容开展3次连环改进的案例，并特别关注他们如何潜意识地运用了基于“重点·难点·关键点”的关键事件分析法，以此引发研究者对教研活动中精髓方法的重视．

1 中国式课例研究的背景

与西方多数国家相同的是，中国的基础教育学校被分为小学、初中和高中3个学段．与西方国家不同的是，中国的学生被组成一个个相对固定的“班”，同“班”的学生一整天共处一室开展学习活动，不同学科的老师游走于不同的“班”．因此同一学科的教师就自然地组成了学科教研组，如数学教研组，就广泛存在于每一所学校．由于数学是核心课程，数学教研组的人数较多时，按照年级再被分为更小的备课组．此外还有区县级、市级和省级的教研室，教研室的学科教研员负责指导相应学科的课堂教学和教学研究活动．这样以来，形成了省级、市级、区县级教研室、学校教研组、学校备课组的多级教研网络[10]．

在多级教研网络中，学校层面的学科教研组始终处于核心地位．中国内地自1952年开始建立学校层面的各学科教研组[12]，并明确规定了学校里学科教研组的“研究”定位：“教学研究组是教学研究组织，不是行政组织的一级．它的任务是组织教师进行教学研究工作，以提高教育质量，而不是处理行政事务”[13～14]．随着20世纪90年代基础教育课程改革的启动，教研组又具有了新时期下把课程改革的理念落实于日常教学的任务[15]，学校教研组开始对实施课程改革负有责任[16]．在2003到2007年之间，这种以校为本的教研活动被教育部通过“创建以校为本的教研制度建设”工作项目在全国范围内得到加强，近十年间全国范围内已经兴起以“校本教研”为主题词的各种层次的教研活动[17]．这种制度保障下的最初作为改进课堂教学的集体教学研究活动，通过六十多年的发展已逐步形成中国特色的课例研究．

2 中国式课例研究所蕴含的思路和方法

在中国的教研文化中，上公开课并被他人观察往往被视为荣誉．教研组长一般倾向于把公开课机会给组内较为年轻的老师并以此加速他们的成长，伴随着开课活动的是课堂观察活动和课后立即开展的研讨．一般此类活动在教研组长主导下，由开课教师首先自述教学设计和感受，然后由组内其他老师自由发表意见．近期由于专业人员的介入，开始引进一些技巧性方法来提高研讨活动的有效性，如前后测技术、课堂观察技术等都是研究人员所倡导的．

在中国传统的教研活动中，“磨课”（同一授课内容在平行班反复几次）形式的研讨活动是比较常见的一种[18]．特别是近年来随着专业人员走进中小学课堂，这种基于教研活动的课例研究日趋精致化，开始注重采用一定的技术方法而不仅仅凭借经验．图1展示了一种教研活动中典型的课例研究流程，至少有3个环节：备课活动；被同行观察的开课活动；课后集体讨论式的议课活动．教研活动中通常的做法是：在参看各种材料的前提下，由某个年级的备课组首先集体讨论并备课，教研组安排每次约两课时的时间请所有的数学教师观课并讨论，然后根据讨论中的建议再由备课组集体备课形成新的教学设计．无论是教研组和备课组，共同目的是通过集体的智慧来改进课堂教学并解决教学中的实际问题，研讨中所有的材料都是开放的，包括教学设计、教学录像以及观察课堂中收集到的数据．

图1 教研活动中的3个典型环节

在六十多年的传统教研活动中，中国教师在潜移默化地应用着一些共通的教学法框架来讨论教学设计、观察课堂并在课后反思讨论，如平常被老师们所俗称的“重点·难点”，一般会直接出现在教师的教案里，“关键点”有时会以“关键环节”出现在教案中、但一般肯定会在口头讨论中出现，它们实际上提供了教师观察课堂和开展课后研讨的一种思维方式．

所谓“重点”是针对这节课的核心目标而言的，关乎学与教的目标，亦即什么是学生必须掌握的数学内容要点、教师要把教学重心放在哪里，反映的是数学学科本质，类似一些美国学者所说的数学的大观念（big idea）．“难点”主要是针对学生的学习过程而言，亦即学生在学习重点时可能存在的认知方面的困难．作为教师，如果能够清晰陈述和预期这种难点所在，才有可能在教学设计中不是简单化用单一方式传递知识，而是预见性地设计教学来帮助学生丰富学习经历．“关键点”是一节课在教学法角度的核心，亦即教师的教学法决策——如何引领学生经历数学化过程、最终帮助学生克服困难和障碍达到教学目标，是上述二者的综合考虑．此外，随着课程改革中对学生实际学习结果的重视，近年来观课教师会根据对学生学习过程和结果的观察记录，来判断学生对于数学学习目标的掌握程度，即“学习效果”，并由此重新审视原来对于“重点·难点·关键点”的把握是否合理，实际上是做某种程度的教学评价．这种通过关注学生的实际掌握情况并以此为依据反馈和调整课堂教学，就形成了一个完整的如图2所示的回路，近期被研究者概括为教学研讨中的“四元分析法”[19]．

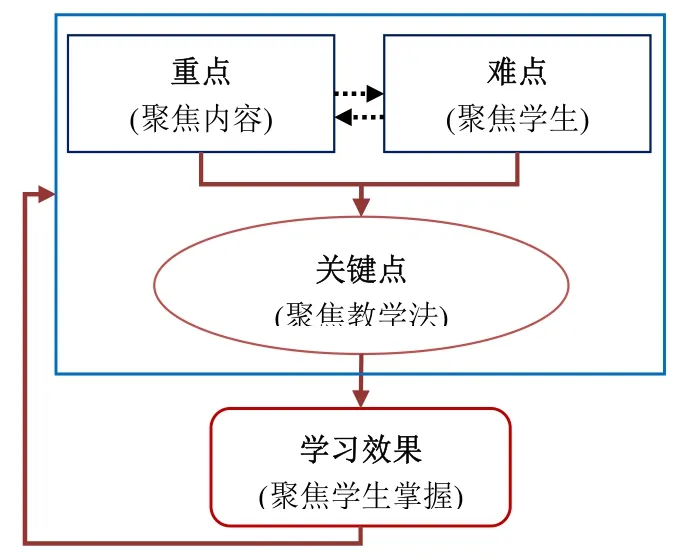
图2 “重点·难点·关键点”与“学习效果”形成回路

当前西方的研究者常常引用舒尔曼的教学内容知识框架[2～3]，来强调特定学科的教师必需有效地掌握教授特定主题内容的知识[20]．中国教师有意识或潜意识所沿用的这种讨论框架，正好反映了教师的教学内容知识分类中一些维度．教师要清晰地辨别出特定教学内容的这几个“点”，不但需要教师自身对相应数学内容深刻理解，而且需要克服学生可能的错误概念所涉及的方法、手段以及表征方面的教学经验．在教研组里，经验丰富的教师往往可以清晰地描述出一节课的“重点·难点·关键点”，而那些经验较为缺乏的教师经常面临困难．教师们在教研活动中逐步学会从这样3个角度分析教学内容和过程，从而用这种结构化的方式逐步提升了自己在备课、开课、教学反思中的专业能力．

在教研活动中，这“三点”和“学习效果”形成的回路，构成了实际教学研讨的4个要素，也可以看成是引发教学讨论的一系列问题：教学目标是什么（重点的分析）？学生到达学习目标需要何种条件（难点的分析）？教学过程怎样设计能够帮助学生克服难点并实现教学目标（关键点分析）？教学最终带来了怎样的学习结果（学习效果的分析）？ 这样4个要素，也可以理解为目标分析、条件分析、过程分析、结果分析，因此被概括为“四元分析法”[19]．中国教师在教研活动中的集体协作是教学实践中自然而然的一部分，它不是由来自外部的某个研究项目驱动，也不是因为外部教育理念的影响或是由感兴趣的专业人员发起．只要成为学校的一名数学教师，就自然而然地成为数学教研组的成员．教研组活动中的集体协作在中国教师的职业生涯中发挥着持续的基于校园生活的专业支持作用，而且这种集体协作的文化也常常通过制度保障下的区县、市、省级的教研室得到加强．

3 研究方法

选择案例研究法来展示教师怎样参与教研活动并改进课堂教学．案例研究的优势在于可以深入分析教师之间的协作以及有利于理性建构．研究中选择了上海近郊一所学校初中部的一个数学教研组及其教研活动作为个案．选择这个教研组有几个原因：第一，上海处于中国教育改革的前沿，教研活动具有一定的引领性；第二，上海的近郊区域的这所学校是中国东部地区典型的城镇学校的代表；第三，上海参加了2009和2012的PISA测试，已经广受国际同行的密切关注．

案例中的数学教研组所在的学校，位于上海市近郊，该区的经济和教育水平在上海17个区县属中等水平，因此该区域和学校均具有一定的典型性．这所学校是社区的配套学校（既非片区的中心校、也非区域的示范校），规模不大，共有9位初中数学教师构成学校的数学教研组．其中3位老师教龄不足5年，4位教师有近10年教龄，2位教师有15年以上教龄．在本研究中，按照教龄从短到长的顺序分别用T1到T9代表数学教研组里9位数学教师．案例中的教研活动，还有一位区教研室的教研员参加（用R1表示）、一位来自市级教育机构的研究者（用R2表示）．

采集了3种主要类型的数据，来反映这个数学教研组以备课、开课、议课为主要环节的教研活动．第一类数据是T1和T6基于集体反馈基础上的教学设计和课堂实录；第二类数据是每一轮授课中观察者所收集到的信息，包括3个平行班的前测和后测；第三类数据是田野式笔记，用以捕捉议课活动中9位数学教师和2位研究者针对“三点”所展开的讨论、争议等内容．在中国内地（包括上海），教研活动的核心是“磨课”——改进课堂教学，因此我们把T1和T6先后执教的3轮授课作为分析的切入口．

研究中的教研组的磨课活动采用了“三次授课、两次反思”的行动教育模式[17]，使用一些课堂观察技术收集数据．授课内容是初中数学“有理数的乘方”，同一内容在3个平行班上了3轮．第一轮和第二轮授课由最年轻的教师T1在他平常任教的两个班执教，第三轮授课由另一位同年级数学教师T6在她平常任教的一个班执教．数学教研组的教师在这次磨课的教研活动中分别承担了不同的角色（表1），一些教师有意识地运用了研究者R2所提供的一些课堂观察技巧．

表1 教师在教研活动中的协作分工

4 研究结果

4.1 第一轮磨课

4.1.1 授课过程

T1的第一次授课持续了46分钟．他使用了一个故事情境来引入乘方的概念．

在古代，有一个聪明的大臣发明了国际象棋并献给国王．国王非常喜欢，于是决定奖励大臣，并让大臣自己提出想要得到的奖赏．大臣说：“陛下，我只想得到一些大米作为您给我的赏赐．假如你在棋盘的第一个方格内放1粒米，第二个方格内放2粒米，第三个方格放4粒米，第四个方格放8粒米，然后依次类推16粒米，32粒米……直到第六十四个方格”．国王哈哈大笑，“你真蠢！只要那么点大米？”大臣不动声色，“陛下，我只担心您的国库里没有那么多大米赏赐给我．”真的没有那么多大米作为大臣的奖励吗？

于是老师和学生一起写下一些算式来计算大米的数量：

第1个方格: 1

第2个方格: 2

第3个方格: 4=2×2

第4个方格: 8=2×2×2

第5个方格: 16=2×2×2×2

……

接下来教师给出了乘方的定义，以及幂、底、指数等概念．整个概念引入过程（包括故事呈现）持续了大约3分钟时间．然后，教师要求学生们阅读课本上关于乘方定义的内容，持续了约5分钟．接下来，教师让学生做了课本上的3道用乘方形式表达同因数相乘的练习，还做了5道课本上的需要辨别底数、指数的题目．在这些做基础练习题目的15分钟那个时间里，T1很关注学生对乘方表达形式的读法．在接下来的近20分钟时间里，T1要求学生做了下面的3组计算题目并订正学生的解答：

最后，教师通过问学生“本节课你学到了什么”来小结，持续了大约3分钟．

4.1.2 教研组讨论中的主要议题

a. 阅读课本可以取代教师的讲解吗？

在课后教研组讨论中，教研组长首先请T1陈述他的教学设计和实际施行情况．T1说：“乘方是初中阶段的一种新运算．我的主要目的是帮助学生掌握幂和其他相关概念，如指数、底数等．……当然，另一个重点是让学生能够做乘方运算．包括我也设计了一组以10为底的计算幂的练习，让学生试着发现规律……”

接下来教研组长请大家自由发言．T2根据她做的课堂教学结构记录指出，建立新的概念乘方总体上只用了8分钟．她说：“我只是感觉仅用8分钟时间建立新概念与做乘方计算所用的时间比太少了……我担心学生是否感觉到了学习乘方的必要性——作为一种相同因数连乘的简便运算．即使在建立新概念的8分钟里，教师只用了3分钟指导而其余5分钟靠学生自己阅读学习”．

T8说：“作为乘方的第一节课，这节课的重心应该是放在帮助学生理解乘方是乘法的一种简便运算，就像乘法是加法的简便运算一样……只是让学生阅读课本去知道一些名词，底数、指数，作用不大．这些概念应该在简化乘法运算形成乘方概念的过程中，它们的意义自然而然就出来了……”

b. 做练习可以取代概念性理解吗？

T7谈到了她在课间休息时访谈到的两位学生的情况．“当我问是否可以解释一下an的意思时，两个学生均指出意思是a×a×…×a，总共有n个a相乘．但其中一个学生说，她不太懂这个故事的结尾……，也就是说她对于1+2+22+…+263计算的结果，到底是多少没有概念．所以说老师只是给出一个数字结果18 446 744 073 709 551 615对学生来说没有意义！学生没有机会体验到乘方运算可以表示一个非常巨大的数字．”T7认为，让学生感觉到当底数大于1时、乘方的增长相对乘法而言是非常巨大的这一点非常重要．

R1也给出了他对于这节课的建议．他认为这节课应该聚焦于获得乘方的概念性理解．他说，“一方面我们有时候会想当然地以为，假如学生做很多的练习，那么他们就自然而然地理解概念了……但这只是一种想法，作为教师应当为学生容易里理解、快速地理解概念搭建脚手架，而不仅仅是立即进行大量练习……另一方面，我们应当减少一些练习的负担，也是课程改革中倡导的一个方向……”

这次课后讨论主要讨论到了上述两个方面的问题，最后数学教研组长做了总结陈述：首先，这节课更应该突出概念形成的过程，不应把它仅仅看成一种运算；第二，在概念应用的过程中，习题的选择要更加精心，应当针对学生易错的地方．

4.2 第二轮磨课4.2.1 授课过程

T1的第二次授课持续了45分钟．首先他仍然采用了第一次授课的关于国王和大臣之间的棋盘故事作为引入情境帮助学生形成乘方这一新概念．

T：棋盘上的每个方格中有多少大米呢？我们把它写下来．

S：（齐答）1, 2, 4, 8, 16, 32…（教师把它们写在黑板上）

当学生直接喊出乘法计算结果有困难时，教师建议不妨采用2的连乘的表达形式记录结果．当有太多的2连乘也写下来很繁琐时，老师继续建议到：

T：哦，假如我们有一个办法写下这么多的2就好了！

S：（一些学生知道并大喊）乘方!

T：是的，这正是今天我们将要学习的一种方法．

接下来，通过把2×2记作22，2×2×2=23，…，2×2 ×…×2=263，T1和学生一起把每个方格的大米的数量就表示出来了．然后教师给出了乘方的概念，指数和底数以及它们的含义．基于对具体数字表达出的乘方概念，T1又一般化为代数式表达的乘方an，然后问到：

T：谁知道263结果是多少？

S：（没人回答但有人喊道）肯定非常大．

T：有多大呢?（学生无语）

T：我已经算出了从22到263所有的计算结果（T1用表格呈现出所有计算结果）…

通过观察22，23，…，263的幂，学生感到非常惊讶，有些结果大得他们根本无法读出来．仅仅是263的结果9 223 372 036 854 775 800就大约相当于23亿5千5百万吨大米，更不用说再把1+22+23+…+263的结果计算出来的大米了！然后教师通过询问学生学过的正方形面积和正方体体积的计算公式，教授了关于乘方的正确读法．整个概念的学习过程大约持续了11分钟．

接下来的10分钟时间里，教师使用了第一节课中设计的第二组、第三组题目作为例题练习．最后，老师用了大约1分钟小结这节课学习的新概念．

4.2.2 教研组中讨论的主要议题

a. 创建的故事情境的价值是什么?

首先，T1表达了他在这节课加强让学生理解乘方概念的想法：“这节课我削减了一些练习题目，更多地关注学生对概念的理解……我花了更多的时间订正学生基础练习中的错误，题目看上去简单却对应用新概念非常重要……”接下来其他老师自由发言．T2补充到，这节课例建立概念用了11分钟，基础练习用了23分钟，教学结构看上去似乎更合理．

T7说，“当我访谈学生，这节课中你印象最深的是什么时，两个学生都说是关于国王和大臣的那个故事．他们说非常惊讶2的63次方是那么大一个数字，这点印象很深．所以，我在想一个好的情境应该如此……”T5接着说，“这节课中我尝试了活动类型转换记录的方法，发现与第一节课相比，这节课中师生互动的活动远远比第一节课多．我在想，一个好的情境应当是能够尽可能地激发学生和老师之间互动的情境……”

T9认为，一个好的情境创设应当是瞄准教学目标但不仅仅是引发兴趣．R2围绕情境这个话题谈到，“一节课中创设的情境，不同的老师使用大概有3种层次．第一层，一些教师仅仅把它看成是激发学生学习热情或者兴趣的工具，但情境可能并没有与学习的内容有密切的关系．但我们不能确信这种激发出的热情或兴趣是否能够持续一整节课，因为它往往激发的是外部动机……第二层次，情境与学习内容有密切关系，是学生学习的动因．这种情境不仅仅激发学生的热情和兴趣，也是从情境开始作为学习新内容的出发点……但最有价值的情境，即第三层次，我们怎样运用这个情境作为学习整节课的一条线索？当然，这个情境同时也可以具有第一和第二层次的功能……”

b. 学生的思维怎样被大问题驱动?

当谈到情境的价值时，讨论的内容似乎离开了这节课具体的内容．T3结合她做的提问回答记录说：“在我对T1的提问记录中，发现问题的类型很多样……总体上这节课有接近70个问题．假如这节课能够按照刚才说的用国王和大臣的故事情境贯穿下去，我想所有的教师提问可能可以组织成几个最重要的大问题．”

T6说，“……下次是我上课，我希望下节课可以用一些大问题来组织教学……毫无疑问，从后测的结果来看，我认为第三次授课中将需要一个主干问题，强调底数……”R2说，“是的，即使在一节课的45分钟时间里教师问了近70个问题，也可能是正常的．但我们需要保持清醒，哪些问题是这节课里最最重要的．学生的思维活动应该被这一系列最重要的大问题来驱动……”

第二次课后讨论得到了这样一些共识：作为情境的故事应当贯穿于这节课，而不仅仅是作为激发动机的一个引子；整节课应当设计为用几个主干的大问题来驱动学生的学习过程．

4.3 第三轮磨课

4.3.1 授课过程

第三次授课由T6施行，持续了大约47分钟．教学过程中使用了一份设计的工作单，上面有7个主干问题作为学生整节课学习的线索．

问题1：国王的国库里足够的大米吗？（用时约17分钟）

T6使用了与第二次授课相同的故事情境激发学生兴趣，并在计算大米的过程中引入了新概念．当学生们对于第64格大米的数量的计算结果感到震惊时，他对学生说：

国王对于乘方能够表示非常大的数目感到惊讶时，他也感到很尴尬，他居然没有那么多的大米来奖励大臣．但国王非常好学也很好奇这种新的乘方运算，他想弄清楚关于乘方的一些问题．然后他引出了下列问题．

问题2：底数究竟是什么？（约12分钟）

问题3：an有多少个零（a=10 or 0.1）？（约6分钟）问题4：(-1)n和0哪一个大？（用时约3分钟）

问题5：乘方有逆运算吗，如( )2=25？（约1分钟）

当上面的问题解决后，T6说：“国王感觉到弄清楚上面的问题后，他已经对乘方有的新的认识，于是他召见了大臣．”由此引出这节课的下一个主干问题．

问题6：国王能够逆转局势吗？（约6分钟）

T6接着陈述了下述故事：

国王对大臣说：“我很抱歉不可能倾国库所有大米回报你．但正如你看到的，我这里倒是有一个一米长的金手杖，从我的先辈哪里继承而来．我决定在7天后把它赏赐给你，但从今天起我每天拿走手杖的一半．”大臣很高兴，他将会得到手杖的一部分，尽管他直觉肯定剩得不多了．那么七天后到底大臣能够得到金手杖的多少呢？

学生通过计算发现，只剩1/128了，算下来还不到8毫米．他们再次惊讶，原来当底数是正数但比1小的时候，乘方的值下降起来也很快！

问题7：你注意到乘方运算有何特点？（约2分钟）

就这样，这节课从问题1到7作为整个教学的主线贯穿下来．

4.3.2 教研组中讨论的主要议题

a. 对学习目标来说有多少练习算足够？

在课后讨论中，T6首先谈到了他的想法和课堂里的做法．“看上去这节课在教学流程上非常清晰……这是因为这节课是用工作单上设计的主干问题驱动的”，他说，“但我只是觉得与前面的第一次和第二次授课相比，这节课学生做的练习不够．这些练习对学生掌握乘方来说足够吗？我这个班上的学生与其他两个班的学生相比成绩会达到相同程度吗？”他的想法显示出他的担心．

T2也表达了同样的担忧，因为用于运算练习的时间大幅下降了．她说：“……在这节课里，问题1可以被看作概念建立阶段，问题2是应用概念的基础练习．这两大主干问题花费了29分钟，接近课的三分之二时间．看上去T6加强了乘方中相关概念的学习，这的确是学习目标，但作为一线教师，我也对学生将来在测验中的分数有相同的担心……”

T8不这么认为．在他迅速浏览了学生的后测结果后，他说：“尽管后测的数据还没有来得及统计出来，但我粗略地看了学生在后测中的情况，T6所授课班级的学生与第二节课班上的学生相比至少有大致相同的学习效果……不管怎样，我认为作为学生学习乘方的第一节课，应该把重点放在强调概念性理解上．至于乘方的运算结果幂，并非第一次学习乘方的主要任务，后面我们仍然有课时可以跟进……”

b. 应当激发何种层面的思维水平？

课后讨论中的另一个焦点是关于问题3，“乘方有逆运算吗，如( )2=25？”．一些老师认为应该在学完整个乘方运算一章内容后再提及．一些老师认为有必要在第一次学乘方时就提出类似的问题做埋伏．

T6说，“当我和T1老师设计这节课教案时，我们觉得乘方第一节课还是有必要提出这样一个后续课程要学的伏笔，给予学生对于乘方及其逆运算的整体观念．”T9也支持类似的想法，他觉得这个问题在这节课里只占用了1分钟时间，是值得的．

R1提出了他对于这个问题的想法．他说：“……在小学阶段，孩子们基于日常生活经验学习了加法，很快他们学习了它的逆运算减法．当一个加数被反复相加的时候，重复相同加数的加法太累了，于是乘法作为一种加数相同加法的简便运算被介绍进来．后来，又学习了乘法的逆运算，除法……乘方作为相同因数乘法的简便运算，被引入了学生的学习过程．类似地，它的逆运算也一定是存在的……所以问题3作为后续内容的铺垫，本质上给予了学生从数学角度认识各种运算怎样一次次演化而来的线索……”R2也做了类似补充：“……尽管第一次学习乘方概念，我们没有必要给出学生乘方逆运算的术语，但作为教师应该帮助学生建立概念之间的联系……我个人甚至认为，T6老师可以在问题3上还可以多花一点点时间，特别是学生在回答之后，教师应当激发学生从以前学过的各种运算之间的关系来思考这个方向……”

5 结果讨论

在教研活动中对3次磨课的描述已经让我们更加清晰地看出了每一次授课的变化，也可以通过比较3次磨课再次回顾和讨论课堂教学到底改进在哪里．

5.1 更多地聚焦学生的概念性理解

回顾《有理数的乘方》3次授课，可以看到在教学结构中有一些共同的环节：（1）用棋盘故事作为情境建立概念；（2）应用新概念的基础练习；（3）计算乘方的幂的练习；（4）由教师做出课堂小结．假如把3次授课用这样4个环节的时间分配表达出来，可以用图3呈现．

图3 3次授课的共同环节及时间分配

从图3中可以看出，每后一次授课，教师花了更多时间用以帮助学生建构概念．第一次授课建立概念虽用8分钟时间，实际上只有3分钟用于创设故事情境并引入概念而后面5分钟让学生自己阅读课本．第二次授课中建构概念的时间已经扩展到11分钟，第三次授课中则多达17分钟（几乎占授课总时长的三分之一）用以帮助学生理解乘方的概念．

如果再具体考察棋盘故事情境是如何建立概念的过程，就会发现3节课的不同．在第一次授课里，故事情境的作用仅仅是激发学生兴趣并获得连乘这种形式，然后很快地在3分钟时间里一般化为乘方的an表达形式．第二次授课中，故事情境扩展为让学生经历概念化的过程，被用作一个问题情境：教师和学生共同计算棋盘上每一格中的大米，当他们在计算乘法结果遭遇困难时，教师建议使用相同因数连乘的表达形式；当连乘的表达形式再次遇到表达形式的困难时，即有太多的2连续相乘，然后教师引进了新的运算——乘方概念．在第二次授课中，故事情境更像是一种问题解决过程，在解决情境中提出的问题的过程中新的概念自然涌现．在第三次授课中，故事情境不仅仅表现为问题解决中导入新概念，更是被用作整节课里贯穿到其他系列问题的引子．通过扩展情境，如国王想要学习关于乘方的更多知识，学生还体会到了乘方的结果幂可以增长得很快、也可能下降地很快．这种使用方式在第三次授课中更有利于学生深刻地理解乘方．

5.2 练习虽然减少但更加精致

在中国内地，学生的计算能力总是被看成是学生学习数学的成功表现．T1在起初第一次授课的设计中，也定位于通过分层的计算练习让学生逐步加深对乘方的理解．第一次课后的教研组讨论，教师们大多认同作为乘方的第一课时不应过多强调乘方计算，而应当把概念性理解放在优先地位：假如学生深刻理解了乘方的意义，计算在学生掌握乘法运算的前提下应该不是问题，所以计算乘方运算的结果幂，不应该成为引入课的主要方向．

计算幂的任务数量在每后一次授课中不断下降：第一次授课中有21道题目，第二次授课中有13道题目，第三次授课总共有8道题目．而且，即使是那些需要计算幂的题目，在设计时也精心地考虑了更加聚焦于新学概念（如底数）的辨别．通过精心设计的练习题目，学生可以掌握运用乘方的关键特征，特别是在底数为负数、分数、或负分数的情况下．用于基本计算的练习时间也从第一次授课到第三次授课在减少．第一次授课中，总共有35分钟时间用于概念性的基础练习和计算幂的练习，第二节课有33分钟，第三节课只有28分钟．时间的减少量看上去很缓慢，没有很大的差异，但考虑到练习题目的数量也在减少，那么就意味着学生在每道精心设计的题目上可以停留更多的时间．

教研组里一些老师担心像第三次授课中那样少的练习数量，是否能够足以保证学生的学习效果不低于第二次授课，因为第三次课中题目数量减少了太多．对此，可以通过比较两个班前测和后测的数据来看学生的学习结果．第二次授课和第三次授课的班级在该年级属于平行班，意味着这两个班在先前的期末考试中成绩表现相近．

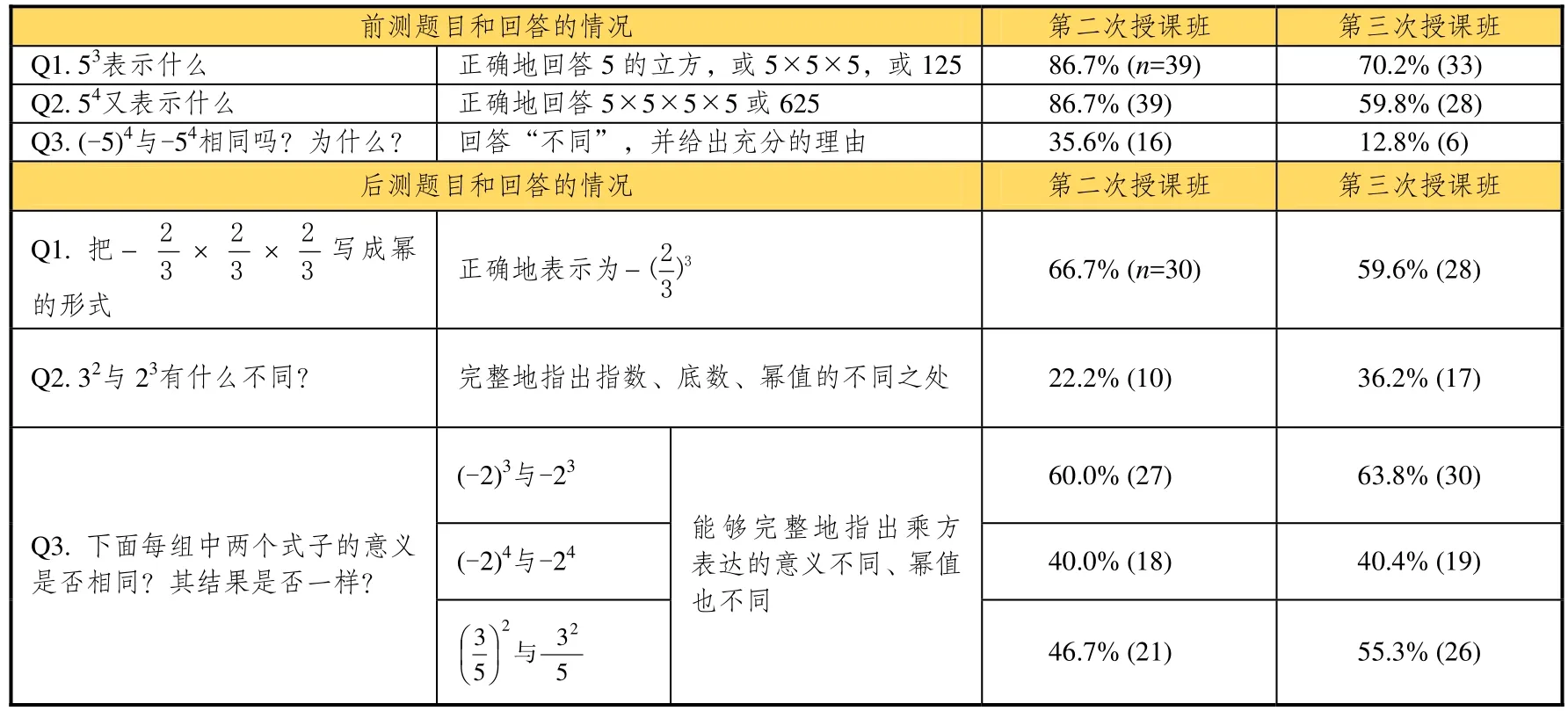
表2 第二次和第三次授课两个班的前后测结果

说明：第二次授课的班有45人，第三次授课的班有47人

从前测的结果来看，第三次授课的班在前测的3道题目的表现上明显要弱于第二次授课的班，这说明第二次授课班的学生相对第三次授课班的学生有较好的基础．但是从后测3道题目的结果来看，除了后测Q1题目表现上第三次授课班略逊于第二次授课班的学生，在涉及概念性理解的Q2和Q3题目上，第三次授课班的学生学习效果要明显好于第二次授课班的学生．看来，正如T6所说，强调概念性理解而削减不必要的练习，并不会降低授课的效果．第三次授课班的学生，考虑到其起点基础略逊于第二次授课班的学生，实际上表现出对于乘方意义和相关概念的更深刻的理解．

5.3 教学在大问题的驱动下更加结构化

根据T3的观察记录，三次授课中教师都问了很多数量的问题．T3把每节课里教师问的部分问题分成两类：“小问题”——那些延伸出的或者扩展理解的细节性追问；“大问题”——那些直接导向新内容探索的主干问题．表3是根据T3老师的记录整理出来的问题数量．

表3 教师在3次授课中的问题类型和数量

自从中国的课程改革施行以来，那种以教师讲授为中心的传统的教学形式一直广受批评，更多的中国教师现在课堂里采用师生间“问—答”互动的形式．T5的教学活动类型观察记录也验证了这种改变．在20世纪末，甚至在上海的一项课堂观察的案例研究中，有研究者发现边问边答的形式正取代教师讲解，一位老师在一节45分钟的课里问了大大小小105个问题[21]．研究者因此指出课堂教学由“满堂灌”变为“满堂问”，过多的琐碎问题往往把本来具有挑战性的问题变成了师生间一唱一和的问答游戏．而且表层的琐碎问题，往往对学生来说局限了他们的思维空间，反而无助于他们思维能力的发展．近期，研究者们开始倡导使用那些与数学学习内容本质相关联的核心问题、大观念来驱动教学[22～23]．

对于每后一次授课中问题数量的减少（无论是大问题还是小问题），研究者把它看作是教研组在集体讨论中不断强调用大观念来组织教学的结果．特别是在第三次授课中，教师设计的工作单上的7个大问题帮助学生在新旧知识之间建立了联系．其中的问题5（乘方有逆运算吗，如( )2=25？）更是帮助学生从数学学科角度整体联系起了运算及其逆运算的演化过程．正如T7所访谈的学生谈到的，“给我印象最深的是这节课的故事，我感觉到数学与生活不是那么遥远”，“乘方来自以前学过的知识，它是为了解决新的问题，我非常喜欢这节课”．T9是教研组里经验最为丰富的老师，直接指出这节课帮助学生理解了乘方是相同因数连乘的简便运算，正如乘法是相同加数连续相加的简便运算一样．这种对乘方的深刻理解，从第一轮磨课后的教研活动中，就为整个教研组确定了这节课的教学目标和重点．

6 结论和展望

尽管大多数中国数学教师学历水平不如西方或日本同行，但中国的数学教师仍然具有较为深刻的对初等数学的理解，有较丰富的数学学科教学知识，并且在教学中连贯地运用这些知识[7～9]．中国数学教师所具有的实践优势，很可能的一个原因就是他们大量地卷入到这种校本教学研究网络中的各种教研活动当中，并且在潜移默化地应用着基于“重点·难点·关键点”的关键性教学事件分析的思维方式．在中国式课例研究中，还有一种“以小见大”生成关键性教学事件的思维方式[10，24]，这里不再赘述．

“相观而善之，谓摩”[25]．从传统文化的角度看，中国教师能够坦然开课并接受来自同行的观察讨论．尽管中国的教师在教研组中的相互协作已经有六十多年的历史，有制度保障下的时间和空间，但这种教研活动仍然也有一些问题存在．如，教师之间的合作和讨论往往更多地依赖经验，教研活动中的协作质量常常取决于教研组长的领导水平，学科内容取向的教研组内的协作同时也隔断了教师与其他学科和学段之间的联系，等等．

考虑到中国内地独特的教育背景，尽管上海的这个教研活动案例反映的中国式课例研究具有典型性，但研究者还是要指出这篇文章中所描述的备课、开课、议课等教研活动仅仅适用于具体的上海课堂，并不能武断地推理到整个中国内地都是这样的面貌．实际上，上海的数学教研活动案例反映了自1990年代数学课程改革以来的一些新特征，但大多数中国内地的数学教研组并非完全一样．

总之，文中案例研究提供了初步的证据来验证研究者的假设，即教师在教研活动中获得了持续改进他们课堂教学实践的能力．当然，研究者也认识到案例研究的局限性．无论怎样，这项研究提供给了数学教育工作者一种对中国式课例研究的理解．尽管西方同行也强调同行互助是比简单地参加工作坊更有效的学习方式[26～27]，但这种方式缺乏来自研究者的有力的理论和专业支持[4]，特别是在中国的课程改革背景下更需要这种支持．作为研究者，这里只是想把这种存在于教研制度中的默会知识显性化出来，并让更多教师有意识地运用到课例研究中并提高教学分析的能力．一项好的研究不一定要来自于假设检验式的演绎，希望更多的研究者可以从优秀的实践中做归纳式研究、而不仅仅是批评实践，也许这正是伯纳德·霍奇森所说的“中国面临的挑战与机遇”[28]．［参 考 文 献］

[1] Anderson L W, Pellicer L O. Teacher Peer Assistance and Review: A Practical Guide for Teachers and Administrators [M]. California: Corwin Press, Inc. 2001.

[2] Shulman L. Those Who Understand: Knowledge Growth in Teaching [J]. Educational Researcher, 1986, 15(2): 4-14.

[3] Shulman L. Knowledge and Teaching: Foundations of the New Reform [J]. Harvard Educational Review, 1987, 57(1): 1-22.

[4] StiglerJ, Hiebert J. The Teaching Gap [M]. New York: The Free Press, 1999.

[5] Ricks T E. Process Reflection in Preservice Lesson Study [J]. Journal of Mathematics Teacher Education, 2011, 14(4):251-267.

[6] Matoba M, Crawford K A, Mohammad R S A. Lesson Study: International Perspective on Policy and Practice [M]. Beijing: Educational Science Publishing House, 2006.

[7] An S, Kulm G, Wu Z. The Pedagogical Content Knowledge of Middle School Mathematics Teachers in China and the U.S [J]. Journal of Mathematics Teacher Education, 2004, (7): 145-172.

[8] Li Y, Huang R. Chinese Elementary Mathematics Teachers’ Knowledge in Mathematics and Pedagogy for Teaching: The Case of Fraction Division [J]. ZDM, 2008, (4): 845–859.

[9] Ma L P. Knowing and Teaching Elementary Mathematics [M]. New Jersey: Lawrence Erlbaum Associates, Publishers, 1999.

[10] Yang Y. How a Chinese Teacher Improved Classroom Teaching in a Teaching Research Group [J]. ZDM, 2009, 41(3): 279–296.

[11] Yang Y, Ricks E T. Chinese Lesson Study: Developing Classroom Instruction Through Collaborations in School-Based Teaching Research Group Activities [A]. In: Yeping Li. How Chinese Teach Mathematics and Improving Teaching [C]. New York: Routledge, 2013.

[12] 教育部．中学暂行章程（政府文件）[Z]．1952．

[13] 教育部．中学教研组工作条例（草案）（政府文件）[Z]．1957．

[14] 钮兆岭．关于新课程背景下教研组活动的思考[J]．数学教育学报，2014，23（2）：75-78．

[15] 教育部．关于改进和加强教学研究室工作的若干意见（政府文件）[Z]．1990．

[16] 国务院．关于基础教育改革的决定（政府文件）[Z]．2001．

[17] 王洁，顾泠沅．行动教育：教师在职学习的革新范式[M]．上海：华东师范大学出版社，2007．

[18] 黄映玲，张檬．提高数学教学的有效性——基于教研组的课堂观察行动研究[J]．数学教育学报，2011，20（3）：67-70．

[19] Yang Y. How Crucial Incidents Analysis Support Chinese Lesson Study [J]. International Journal for Lesson and Learning Studies, 2012, 1(1): 41-48.

[20] 韩继伟，黄毅英，马云鹏．中学数学教师的学科知识[J]．数学教育学报，2009，18（5）：42-45．

[21] 周卫．一堂几何课的观察与诊断[J]．上海教育，1999，（6）：11-14．

[22] 杨玉东，李士锜．用本原性数学问题驱动课堂教学[J]．数学教育学报，2005，14（2）：59-63．

[23] 徐文彬，杨玉东．本原性问题及其在数学课堂教学中的应用[J]．数学教育学报，2005，14（3）：14-16．

[24] 杨玉东．教研要抓住教学中的关键事件[J]．人民教育，2009，（1）：48-49．

[25] 杨天宇．礼记译注[M]．上海：上海古籍出版社，1997．

[26] Signh K, Shifflette L M. Teachers’ Perspectives on Professional Development [J]. Journal of Personnel Evaluation in Education, 1996, 10(2): 145–160.

[27] Sparks G M. The Effectiveness of Alternative Training Activities in Changing Teaching Practices [J]. American Educational Research Journal, 1986, 23(2): 217–225.

[28] 伯纳德·R·霍奇森．数学教育的社会文化研究：中国面临的挑战与机遇[J]．数学教育学报，2010，19（5）：1-3．

Employing Crucial Incidents Analysis to Support Chinese Mathematical Lesson Study

YANG Yu-dong1, WANG Xiong2
(1. Shanghai Academy of Educational Sciences, Shanghai 200032, China; 2. Shanghai Normal University, Shanghai 200234, China)

Teaching Research Organization is a part of China-characteristic educational system and mathematics Teaching Research Group (TRP) almost exists in every school in China. By a case study of a mathematics TRG activities, the improving process of three lessons on a same topic was presented, which is based on crucial incidents analysis method, so called Key Point, Difficult Point and Critical Point, consciously or unconsciously used by frontline teachers. In view of the case of TRG, features of this kind of collective discussion to improve lessons were summarized and the author expected more and more Chinese teachers could inherit the pith in traditional TRG activities and intentionally employ it in mathematical lesson studies.

lesson study; teaching research group activities; crucial incidents analysis; key point; difficult point; critical point

G420

：A

：1004–9894（2015）03–0040–08

[责任编校：周学智]

2015–02–19

教育部重点课题——数学问题情境创设的有效性研究（GIA117010）

杨玉东（1975—），男，甘肃武威人，博士，副研究员，从事数学教师教育方向研究．