高中生数学学习非智力特征调查问卷的编制

王光明，宋金锦，王兆云

（1．天津师范大学 教师教育学院，天津 300387；2．加拿大多伦多大学 教育学院，多伦多）

高中生数学学习非智力特征调查问卷的编制

王光明1，宋金锦1，王兆云2

（1．天津师范大学 教师教育学院，天津 300387；2．加拿大多伦多大学 教育学院，多伦多）

关注学生的学习活动，也要关注学生的数学学习活动，编制反映与高中生数学学习密切相关的非智力心理特征的调查问卷，将会为高中生数学学习非智力特征的评估与量化研究提供工具．在梳理国内外相关研究的基础上，咨询专家意见，构建高中生数学学习非智力特征调查模型，依据模型编制适用于高中学生的数学学习非智力特征调查问卷，通过多次施测修订问卷．数据分析表明调查问卷结构合理，信度、效度符合心理测量学要求．数学学习非智力特征调查问卷可以作为进一步研究的工具使用．

非智力因素；数学学习；问卷编制

1 目 的

学习活动中，智力因素和非智力因素共同制约着活动的效率，其中非智力因素起决定性作用[1]．1935年美国心理学家Alexander提出非智力因素的概念后，国外学者展开了对其理论的探讨与实践研究，并编制出CTI、NCQ等广泛应用的测量工具．20世纪80年代起，中国学者开始从理论上探讨非智力因素的含义与作用[2～6]，并通过实证研究验证了非智力因素与学习成就的相关关系[7～11]．在测量工具方面，经历了由借鉴国外相关量表，到自编量表（问卷）的阶段，“中国少年非智力个性心理特征问卷（CA-NPI）”、“中小学生非智力因素调查问卷”、“小学生非智力因素问卷”是由中国研究者编制的非智力心理特征测量工具的代表．但目前国内非智力心理特征测量工具缺乏学科的针对性，笼统地询问学生“你害怕考试吗”、“你觉得学习辛苦吗”等问题有欠妥之处．

研究旨在分析影响数学认知活动质量与效率的非智力心理特征，尝试建构数学学习非智力特征的模型，并依照该模型编制能够反映与高中学生数学认知密切相关的非智力特征的问卷，为数学学习中非智力心理特征的评估与量化研究提供工具．研究的大致程序是：文献的积累并咨询专家意见——模型构建——形成初始问卷——修订问卷——正式问卷的编制与修订——正式问卷的形成，主要分析工具为SPSS18.0及LISREL8.8软件．

2 数学学习非智力特征调查模型的建构

2.1 文献梳理

美国心理学家Brown曾经提出在进行智力测验时应当考虑性格特质的因素，Alexander首次使用了非智力因素（Non-Intellective Factors）这一术语．Alexander发现，在智力测验中，有些起作用的变量被忽视，它们包括个体气质、兴趣和趋向性，这些因素和一般智力因素一起影响着学生的学业成就．在他的启发下，Wechsler提出了“智力中的非智力因素”这一概念，主要指气质和人格因素，尤其是人格因素，后将非智力因素的涵义概括如下：（1）从简单到复杂的各种智力水平中都反映了非智力因素的作用；（2）非智力因素是智慧行为的必要组成部分；（3）非智力因素不能代替智力因素的各种基本能力，但对智力起制约作用[12]．Wechsler的这一界定得到西方学者认可，但在非智力测量方面他认为只是在智力测量过程中加以考虑即可．Epstein和Meier提出的应用性智力，是一种由非智力因素构成的“建设性思维”（Constructive Thinking），他们设计的“建设性思维测验”（CTI），所测内容包括情绪控制、行为控制、思维定型、迷信思维、内在乐观性、否定思维6个维度[13]．Tracey和Sedlacek设计的“非认知问卷”（NCQ）主要测查了与大学生学业成功相关的8个非智力因素，即自信、符合实际的自我评估、正确理解对待种族歧视、目光远大、借助权威、成功的领导经验、乐群、在某一领域所获得的知识[14]．除以上较为综合的非智力测量工具之外，Pintrich等人编制的“学习动机策略问卷”[15～16]（Motivated Strategies for Learning Questionnaire，MSLQ）是目前在多国被广泛应用的测量工具之一，主要测查的是学生的学习动机与策略，其中动机分量表包含外驱动机、内驱动机、任务价值、信念调控、自我效能、考试焦虑6个维度，该问卷中关于学习效能感、考试焦虑的题目也为多国研究者所借鉴、使用[17]．

在中国，燕国材多年来对非智力因素进行了广泛的研究，将非智力因素分成广义、狭义和具体3个层次[6]：广义的非智力因素，指认识智力因素以外的一切心理因素；狭义的非智力因素，由动机、兴趣、情感、意志和性格5个基本心理因素构成；具体的非智力因素，将狭义的5种基本非智力因素细分为12种具体的非智力因素，包含成就动机、求知欲望、学习热情、自尊心、自信心、好胜心、责任感、义务感、荣誉感、自制性、坚持性和独立性．上海黄浦区“初中学生非智力综合实验课题组”在课题研究中借助“集合”来界定非智力因素[18]：若心理现象这个整体为全集I，智力因素构成的集合A是I的一个子集，A的补集显然也是I的一个子集，即有A∪=I，内所有元素为非智力心理因素．林崇德认为非智力因素的结构包括了情感过程、意志过程、个性意识倾向性、气质和性格[5]．沈德立将智力活动比作学习活动的操作系统，而非智力因素则对活动起着调节和动力作用，其团队编制的“中小学生非智力因素调查问卷”中包含了成就动机、交往动机、认识兴趣、学习热情、学习焦虑、学习责任心、学习毅力、注意稳定性、情绪稳定性、支配性和好胜心11个分量表[3]．在此之前，由中国超常儿童研究协作组少年个性组编制“中国少年非智力个性心理特征问卷”（CA—NPI）将下列6项因素（特征）作为测试的内容：抱负、独立性、好胜心、意志坚持性、求知欲及自我意识[19]．

非智力因素，是一个从较概括的层面上提出的概念．通过对上述测评工具的梳理可得，目前已有工具在测评维度与内容上均有不同，可见将非智力心理特征量化研究的复杂性．研究者赞同林崇德对非智力因素范围的界定：非智力因素是在智力活动中表现出来的心理因素，而不包括诸如豪爽、大方等与智力活动无关的心理因素，即它不是指智力因素之外的一切心理因素，而是在智力活动中影响决定智力活动效益与智力活动有关的一切心理因素．数学学习过程中的非智力特征，则是不直接参与认知活动，却与数学认知活动的质量和效率密切相关的心理因素．

2.2 数学学习非智力特征调查模型的初步建构

文献梳理之后，研究者于2014年5月—2014年7月期间，分别对国内外多位知名专家学者进行访谈．其中，包括加拿大多伦多大学教育学院Douglas McDougall教授（曾任加拿大数学教育心理学会主席，2014年5月12日在天津师范大学接受专门访谈），香港大学梁贯成教授（教育部长江学者，2013年国际数学教育最高成就奖费莱登特尔奖获得者，这是全球数学教育界的最高荣誉，也是首位获颁此项国际殊荣的亚洲学者，于2014年5月23日在北京师范大学接受专门访谈），美国特拉华大学蔡金法教授（应全美数学教师理事会（NCTM）之邀作为第三本《数学教与学研究手册》（Third Handbook of Research in the Teaching and Learning of Mathematics）的主编，于2014年5月23日在北京师范大学接受专门访谈），澳大利亚墨尔本大学David Clarke（墨尔本大学国际课堂研究中心主任，于2014年6月28日在甘肃省委党校宾馆接受专门访谈）、美国范德堡大学Paul Cobb教授（2005年国际数学教育最高成就奖费莱登特尔奖获得者，于2014年7月1日在北京师范大学接受专门访谈）等专家．在访谈过程中，就问卷维度的确定以及题目的编写等具体问题征求了专家的意见．

进而确定了数学学习中主要涉及的几种非智力心理因素，分别为动机、兴趣、情绪情感、态度、意志和性格，并初步细化出了共计12个测量因子．至此，如图1所示，数学学习非智力特征的调查模型已初步构建出．

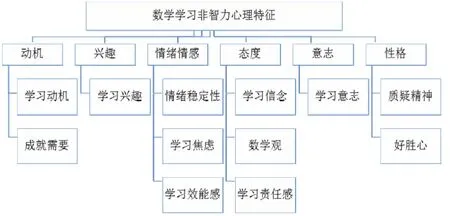
图1 数学学习非智力特征调查模型

位于模型第一层的是数学学习非智力特征，指的是不直接参与数学认知活动，但与数学认知活动的质量和效率密切相关的心理因素，即非智力的心理因素不像记忆、思维、想象等心理成分直接作用与智力活动，但影响、制约着智力活动进行．第二层是数学学习非智力特征中6种主要的维度，动机维度主要指的是数学学习动机，即激励和指引个体进行数学学习的一种内部动力．兴趣是个体倾向于认识、研究、获得某种知识的心理特征，可以推动个体求知的一种内在力量，如果对某一内容有兴趣，就会持续地专心致志地钻研它．情绪情感是个体在学习过程中产生的体验，也外显为身体或生理变化．态度是个体对学习活动或所学课程的一种带有评价意义、较为理性的认识和理解．意志是个体自觉地确定学习目的，并为实现预定目标克服困难、自我控制的心理过程．性格维度主要体现在个体对自己、对别人、对事物的态度和所采取的言行上，是较为稳定、长期的精神状态．模型的第三层水平，是12项更为具体化的因子，表1对12项因子做了具体的介绍．

3 方 法

3.1问卷题目的收集与编制

3.1.1 借鉴与改编

问卷所含题目的来源之一，是选取国内外相关的高质量量表（问卷）中部分试题进行改编．例如“学习动机策略问卷”（下简称MSLQ），包含了外驱动机、内驱动机、任务价值、信念调控、自我效能、考试焦虑等维度，研究问卷中学习动机维度的试题从MSLQ的内驱动机、外驱动机试题组中选择6个项目加以翻译并改编，使试题更有数学学习的针对性，更贴近高中生数学学习的过程．除此之外，问卷中的部分题目还参考了挪威心理学家Gjesme和Nygard编制，叶仁敏等人译制的“中学生的成就动机量表”（下简称AMS）、“数学焦虑评定量表”（下简称MARS）、“数学观调查问卷”（简称VAMS）、“中小学生非智力因素调查问卷”[3，20～22]．

表1 数学学习非智力特征调查模型因子介绍

3.1.2 专家指导下的自编题项

问卷所含题目的来源之二，是根据前期文献梳理并结合专家的研究经验，将准备测量的项目用学生熟悉的语言，简练地表达出来．如在数学学习动机因子中，除改编自MSLQ的6个题目，有4个题目为自编试题．各因子试题来源整理如表2．

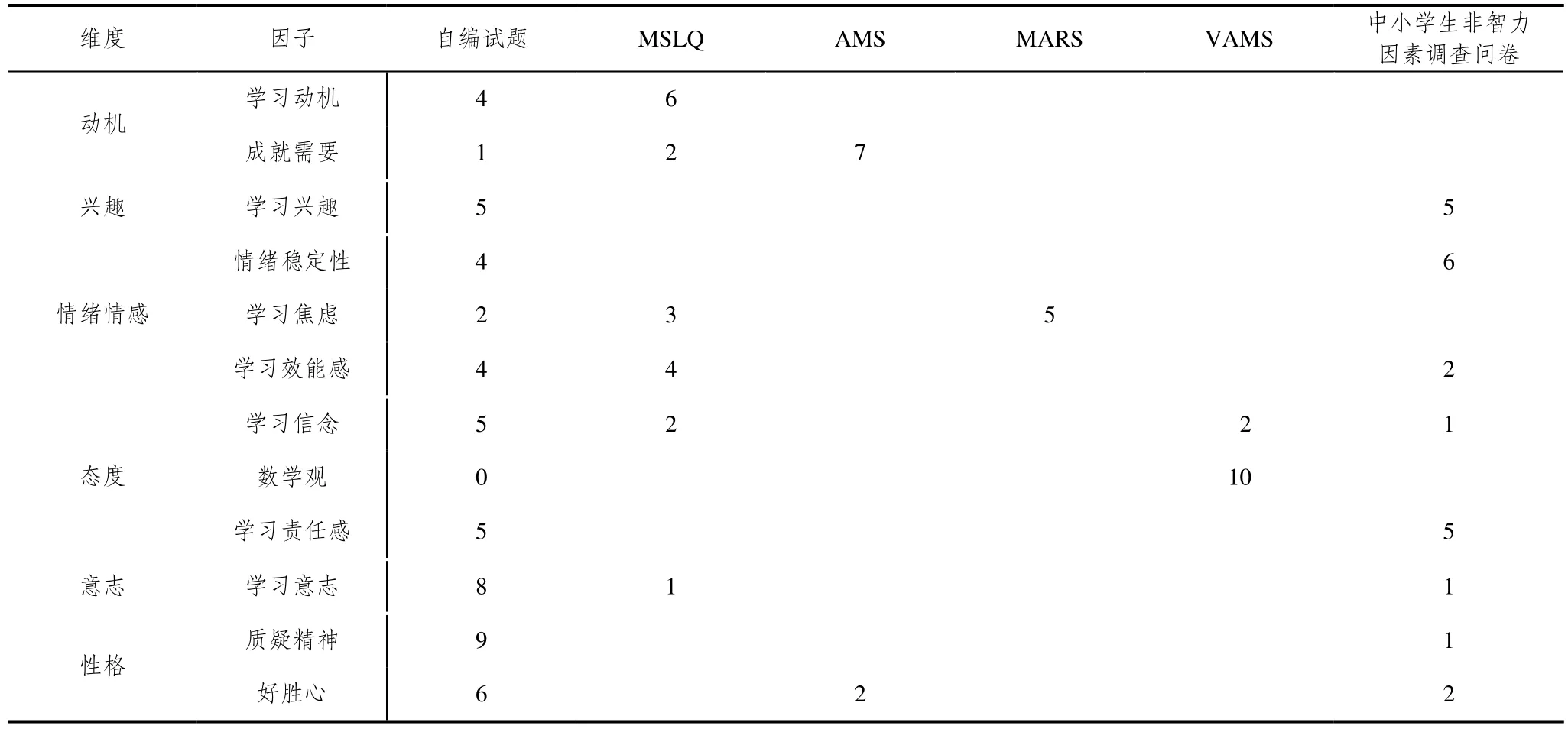
表2 数学学习非智力特征调查问卷题目来源

3.1.3 信度问卷的确定

信度问卷采取重复题目的形式，从问卷中随机选取5个题目为参照，拟定5组重复题目，混合编排在问卷内，若被试在同一组题目中前后两次回答差异过大，则可认为被试没有认真对待，其作答结果也视为无效．

经过初步编制，数学学习非智力特征调查问卷（第一版）包含6个维度和一个信度问卷，共计12个因子125个题目．所有试题混合编排，试题选项均为A非常符合、B符合、C基本符合、D不太符合、E根本不符合，要求被试根据自身情况选择最合适的一个选项．评分方式采取五级评分制，对不同选项赋予相应的分值．

3.2 问卷题目的初步修订

为检测数学学习非智力特征调查问卷（第一版）的题目质量，研究选取天津市内第四中学、十四中学、二十中学、二十一中学、海河中学、扶轮中学，天津郊县的大白中学、大口屯中学8所学校中300名学生作为被试施测．数据回收后经两个步骤对300位被试作答结果进行筛查：（1）目测，漏答题目大于等于5个、或多选题目大于等于2个、或答案存在同一性、规律性、周期性的情形视为无效结果．（2）可信度检验，通过信度问卷对经过目测筛选后的问卷再进行检验．经两步筛查获有效答卷263份，数据的进一步分析处理如下：

3.2.1 项目分析

3.2.2 探索性因素分析

以维度为单位，选用主成分分析法，抽取因素的特征根限定大于1，以最大方差法进行旋转进行探索性因素分析，题目删减的原则是：（1）删除因子载荷值小于0.35的题目；（2）删除在两个或两个以上因子载荷比较近似的题目；（3）每个因子最少应该包含3个题目，逐步排除某些极端题目．经多次的探索过程，相继剔除20个题目．

通过项目分析及探索性因素因素分析，数学学习非智力特征调查问卷（第一版）中的82个题目予以保留，动机、兴趣、情绪情感、态度、意志、性格6个维度的题目数量分别为14、8、21、18、8、13．为了保证问卷的可信度，增加5个题目组成的信度问卷，用以作为剔除无效问卷的参考标准之一．最后，将87个题目交叉混合排列，形成了数学学习非智力特征调查问卷（第二版）．

3.3 正式问卷的编制

3.3.1 被 试

研究采用整群随机抽样的方法，样本取自天津、湖北、新疆3个测试点的7所高中，共968名高中学生参与调查．作答结果回收968份，经两步筛查（筛查方法与上文一致）剔除52份无效答卷，最终获有效答卷916份，问卷有效率为94.63%．

3.3.2 材料

数学学习非智力特征调查问卷（第二版），根据研究者预先的模拟，98%的被试可以在10—20内分钟内作答完毕．

3.3.3 程 序

对回收数据进行处理，通过因素分析，对问卷的理论调查模型进行检验、修正，从而确定正式问卷的体系结构，并计算问卷的信、效度指标，考察数学学习非智力特征调查问卷的质量．

4 结 果

4.1 探索性因素分析

分别对6个维度的项目进行KMO值和Bartlett’s检验，如表3数据显示，各维度所含项目的KMO在0.84—0.93之间，Bartlett’s检验的χ2值均达到显著（p<0.01），即所测群体的相关矩阵间有共同因素存在，适合因素分析．

表3 6个维度KMO与Bartlett’s检验

选用主成分分析法，抽取因素的特征根限定大于1，以最大方差法进行旋转对6个维度的题目进行探索性因素分析，题目删减的原则与上文相同．经探索过程，删除题目59（我对数学知识的掌握不如班里大部分同学掌握的好）、65（对于数学考试中的附加题，我通常不理会）、78（数学学习过程中感到困惑时，我会向教师提出“这道题为什么这样做”等类似问题）、12（我喜欢将课本上的数学知识与自然现象、日常生活中的问题联系）、47（在数学知识方面，如果我能够思考出一些独特的见解，我会感到有意义而又快乐，而不是浪费时间又伤脑筋的苦差事）．兴趣、情绪情感、态度、性格4个维度内抽取出的因子数目与各因子包含的题目与预先设计的题目接近并趋于稳定，因此不再重新命名．动机、意志维度的因子提取数目与之前构想有所出入，其中动机维度特征值大于1的因子有3个，意志维度抽取特征值大于1的因子有2个，如表4所示．根据题目的具体内容，将抽取出的因子命名：题目1、10、31主要是指对数学学习内容本身感兴趣而学习数学，14、36、86、40项涉及到家长、教师的表扬、高考、物质奖励等数学学习的外部动机，题目15、41、11、37、13、24、2主要涉及努力提高数学方面的成就、挑战难题、展现能力方面的内容，因此将动机维度3个因子分别命名为内部动机、外部动机、成就需要；题目6、23、46、56主要是指有意识地、自觉地为数学学习付出努力，项目53、58、81、83主要涉及数学学习中坚持、克难等意志品质，因此将意志维度抽取的因子分别命名为自律性、坚持性．6个维度内提取出因子的累计解释变异量在73.77%—53.62%之间，剩余77个项目在其所属因子上的载荷值在0.35—0.83之间．

4.2 验证性因素分析

4.2.1 一阶因子验证

根据探索性因素的结果，数学学习非智力特征调查问卷（第二版）保留了77个项目，包含14个一阶因子、6个二阶因子，对这一初始模型的一阶因子进行检验，模型得到识别．选取χ2、df、RMSEA、和NFI、NNFI、CFI、GFI为模型拟合程度的评价指标，标准为χ2/df在2.0到5.0之间，RMSEA低于0.1，GFI、NFI、NNFI、CFI超过0.9则认为模型可以接受[23]，其中χ2/df、RMSEA越低，GFI、NFI、NNFI、CFI越高模型拟合越好．原模型的各项拟合指数见表4，其中RMSEA、GFI较不理想．因此依据题目的因子负荷、修正指数MI及对其他参数估计的观察，对问卷题目进行删除或重新评估其归属，以对模型进行适当调整．

表4 动机与意志维度探索性因素分析摘要表

4.2 验证性因素分析

4.2.1 一阶因子验证

根据探索性因素的结果，数学学习非智力特征调查问卷（第二版）保留了77个项目，包含14个一阶因子、6个二阶因子，对这一初始模型的一阶因子进行检验，模型得到识别．选取χ2、df、RMSEA、和NFI、NNFI、CFI、GFI为模型拟合程度的评价指标，标准为χ2/df在2.0到5.0之间，RMSEA低于0.1，GFI、NFI、NNFI、CFI超过0.9则认为模型可以接受[23]，其中χ2/df、RMSEA越低，GFI、NFI、NNFI、CFI越高模型拟合越好．原模型的各项拟合指数见表4，其中RMSEA、GFI较不理想．因此依据题目的因子负荷、修正指数MI及对其它参数估计的观察，对问卷题目进行删除或重新评估其归属，以对模型进行适当调整．

表5 一阶14因子模型拟合指数

通过对原模型M1ord-1各项参数的观察，题目69（当我的答案与练习册上答案不一致时，我会再次认真演算，但不会排除练习册出错的可能）在因子“质疑精神”中的载荷为0.30，其在因子“自律性”中的MI是106.52，显示它可能归属于该因子，结合该题目的具体意义，尝试将其归入因子“自律性”，因此产生了一阶验证模型M1ord-2．此外，在数学教育心理学中，认为兴趣具有动力和维持功能，能够直接转化为人们的学习动机，成为人们从事某种活动的内在动力[24]；也有学者将兴趣作为数学学习认知性动机的一个层次[25]，结合这一理论推导，将因子“内部动机”与“学习兴趣”合并，命名为“认知性动机”，由此产生的模型M1ord-3．调整后模型的拟合度指标如表6．结果表明，模型M1ord-2与M1ord-3都是可以接受的，基于模型的简洁性原则，选取M1ord-3，即原模型一阶14因子修正为13因子，分别为：认知性动机、外部动机、成就需要、情绪稳定性、学习焦虑、学习效能感、数学观、学习态度、学习责任感、自律性、坚持性、质疑精神、好胜心，所有题目在一阶因子上的标准化载荷在0.40—0.89之间．

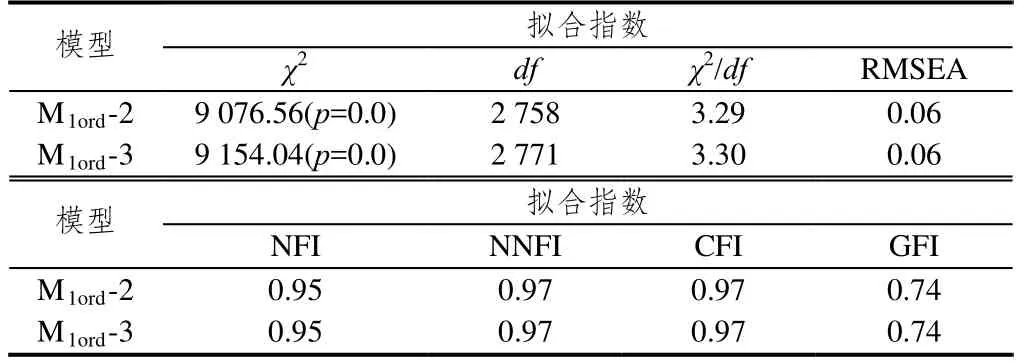
表6 一阶因子模型的拟合指数

4.2.2 二阶因子验证

根据一阶因子验证分析，将学习兴趣与内部动机合并，因此二阶因子减少为动机、情绪情感、态度、意志、性格，将该结构定义为模型M2ord，进一步对问卷的二阶因子模型进行验证，结果如表7所示．χ2/df和RMSEA均优于一阶模型，CFI与NNFI达到可接受的水平，因此将M2ord作为最终确立的数学学习非智力特征的合理调查模型．

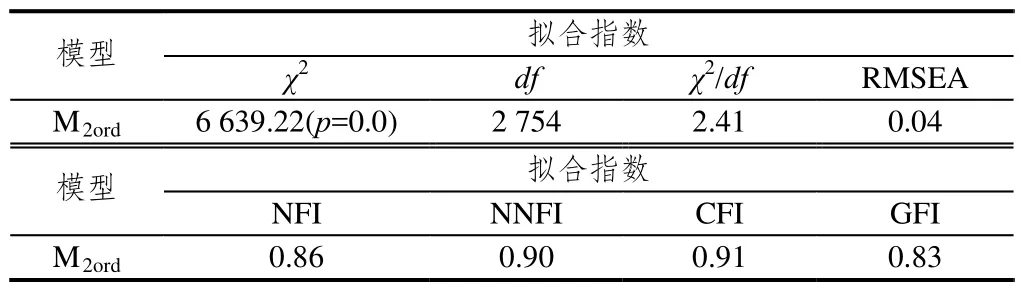
表7 二阶因子模型的拟合指数

77个项目在一阶因子上的标准化载荷在0.40—0.88之间，其中97%的项目在一阶因子上标准化载荷在0.50—0.88之间；各一阶因子在二阶因子上的标准化载荷在0.40—0.94之间，反应出该模型拟合较好．图2为数学学习非智力特征调查问卷五维度模型标准化路径图．

4.3 信度指标

为反映问卷的稳定性，研究者对天津地区参与高中生数学学习非智力特征调查问卷（第二版）调查的104名学生进行了再测，时间间隔为16周．分别计算动机、情绪情感、态度、意志、性格5个维度分问卷及总问卷的同质性信度、分半信度及重测信度，结果（表8）表明，动机、情绪情感、态度、意志4个分问卷的Cronbach's α系数都在0.80以上，性格维度的α系数相比较低．总问卷的α系数达到0.90以上，表明问卷具有较高的同质性；问卷整的重测信度接近0.86，表明问卷具有较好的稳定性．结合各项信度指标，认为高中生数学学习非智力特征调查问卷具有较高信度．

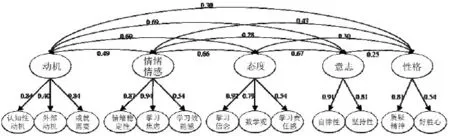
图2 数学学习非智力特征调查问卷五维度模型

表8 正式问卷的信度指标

4.4 效度指标

4.4.1 内容效度

问卷编制过程中，题目内容参考了国内外文献中已有量表（问卷），并力求题目内容符合中国高中生数学学习的实际；此外，根据国内外专家的审查、反馈和意见，构建调查模型、对问卷中存在问题的题目进行修改或删除，确定了数学学习非智力特征调查问卷的题目．之后又先后邀请了天津师范大学白学军教授、北京师范大学曹一鸣教授、华东师范大学鲍建生教授、首都师范大学连四清教授4位专家对问卷中每一题目与其所属维度的相关性做出评价（采用4级评分法），通过计算内容效度指数（content validity index，CVI）来评判问卷内容效度的优劣．根据结果，四位评价者间的一致性水平为0.80，表明评价者间一致性较好．计算条目水平的I-CVI，结果（表9）显示问卷中有62个题目I-CVI为1.00，即这62个题目得到4位专家的一致认可，具有很高的内容效度；剩余15个题目的I-CVI为0.75，对随机一致性进行校正后K*为0.67，提示内容效度良好．进一步计算量表水平的内容效度指数，结果显示S-CVI/UA为0.80，S-CVI/Ave为0.95．根据S-CVI/UA不低于0.80，S-CVI/Ave应达到0.90中，题目内容参考了国内外文献中已有量表（的标准[26～27]，高中生数学学习非智力特征调查问卷的内容效度良好，部分题目还有进一步修订的空间．

表9 正式问卷的内容效度指标

4.4.2 结构效度

以问卷各维度之间及各维度与总问卷之间的相关系数作为结构效度的指标之一．计算结果如表10所示，问卷5个维度间存在显著相关，相关系数在0.26—0.62之间，5个维度间存在中等程度的相关．由此可判断5个维度既能对整个问卷做出贡献，同时又具有一定的相对独立性．另一方面，5个维度与总问卷间的相关系数均明显高出维度间的相关系数，表明问卷整体的结构效度良好．之间及各维度与总问卷之间的相关系数作为

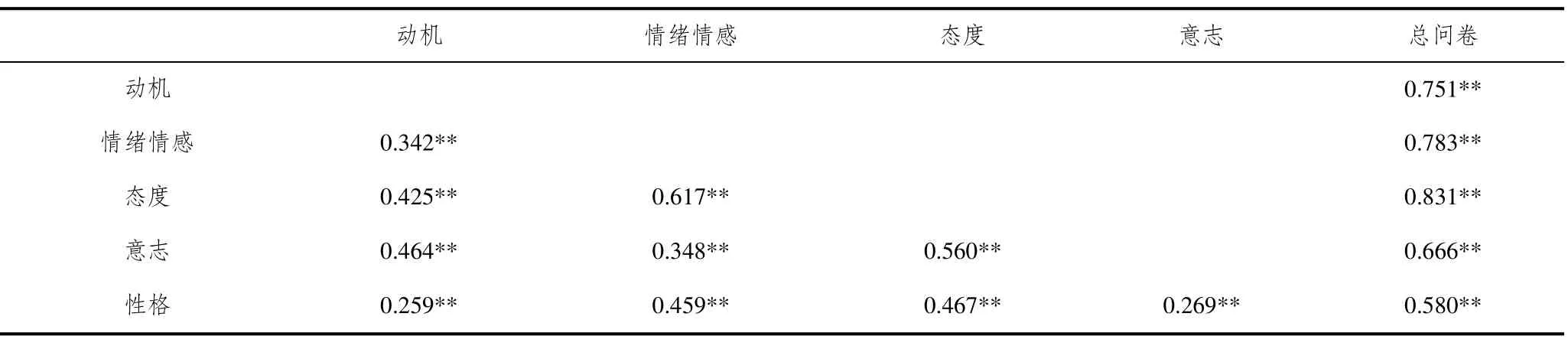
表10 各分问卷间及与总问卷间的Spearman相关系数

以验证性因素分析所显示的二阶模型拟合指标作为结构效度的指标之二．一般来说，RMSEA经验值在0.08以下（越小越好），NNFI和CFI在0.9以上（越大越好），所拟合的模型是一个“好模型”[23]．根据表7中的拟合指标，认为高中生数学学习非智力特征调查问卷的一阶13因子二阶5因子模型可以接受．

5 讨论与结论

研究通过文献的梳理，结合专家意见，初步建构了数学学习非智力特征的调查模型，形成了“高中生数学学习非智力特征调查问卷（第一版）”，经测试修订出“高中生数学学习非智力特征调查问卷（第二版）”，在二版测试数据的基础上，参照项目分析及因素分析的结果，对调查模型进行修订，确立调查问卷的结构模型．与中国较为常用的“中小学生非智力因素调查问卷”[3]包含11项非智力因素的结构相比，“高中生数学学习非智力特征调查问卷”与之主要有3点的不同：一是将学习兴趣并入认知性动机，研究认同兴趣是数学学习动机的一个层次的说法，认为兴趣是开展数学学习直接动机，具有推动、指引和维持数学学习的功能．其次，在问卷中加入了对数学观的测查．研究将高中生的数学学习态度分为了对数学的认识、对数学学习的认识及对自身与数学学习间关系的认识，即数学观、学习信念与学习责任感3个因子，更具有学科针对性地测查学生的学习态度．第三，质疑精神在数学研究的猜测、错误和尝试、证明与反驳、检验与改进等活动中发挥着重要作用[28]，同时“不会被动地接受，敢于大胆的质疑”也是高效率数学学习学生的特征之一[29]，基于质疑精神对高中生的数学学习的重要影响，研究将其列为测查因子加入到问卷结构中．

最终确定的正式问卷分为动机、情绪情感、态度、意志、性格5个维度，共包含82个题项，其中动机维度包含20题，分为认知性动机、外部动机和成就需要3个因子；情绪情感维度20题，分为情绪稳定性、学习焦虑和学习效能感3个因子；态度维度18题，分为学习信念、数学观、学习责任感3个因子；意志维度9个题目，分为自律性和坚持性两个因子；性格维度10个目，分为质疑精神和好胜心两个因子；信度问卷包含5个题目．问卷的测量学属性检验结果表明，结构模型的拟合指标达到可接受水平，问卷整体的α系数为0.95，分半信度为0.80，重测信度为0.86，说明“高中生数学学习非智力特征调查问卷”结构合理，并具有较好的内部一致性与稳定性，可以作为高中生数学学习非智力特征调查与评测的工具使用．

研究针对中国高中阶段学生，编制了“高中生数学学习非智力特征调查问卷”，该问卷可为今后高中生数学学习中非智力心理特征的评估与量化研究提供工具．依据研究工具形成了How Chinese High School Students Develop Learning Strategies in Mathematics Education，该文被第13届国际教育大会（HICE）（2015年1月5—8日）接受，并做大会分组交流．另一文Chinese High School Students’ Cognitive and Non-intelligent Ability Development in Mathematics Learning（2015年4月15—16日）已经被华人教育大会接受．同时，还给天津市部分高中开展了数学学习非智力诊断研究，譬如，研制了“天津汉沽一中高二学生数学学习非智力特征调查报告”，受到了基础教育的欢迎．

当然，研究还存在一些局限：（1）各因子题目数量在4—9之间，题目数量有些不均；（2）问卷的二阶因子结构拟合度并不明显优于一阶因子结构拟合度；（3）部分题目内容效度指数不理想．在今后的研究中，针对问卷的二阶结构、内容效度较低的题目还可做进一步的修订与完善，并制定全国常模、编制问卷使用手册．高质量的问卷需要实践中的使用和修订，在此，欢迎有兴趣的读者对研究问卷进行更大范围的检验、修订，进一步提高“高中生数学学习非智力特征调查问卷”的质量．

[1] 沈德立，白学军．高效率学习的心理机制研究[J]．心理科学，2006，（1）：2-6．

[2] 燕国材．关于非智力因素的几个问题[J]．上海师范大学学报（哲学社会科学版），1988，（4）：134-139．

[3] 沈德立，李洪玉，阴国恩．非智力因素的理论与实践[M]．北京：教育科学出版社，1997．

[4] 燕国材．关于IN结合论的十对命题[J]．心理科学，2001，（21）：519-522．

[5] 林崇德，俞国良．对“非智力因素”争议问题的几点看法[J]．中国教育学刊，2005，（2）：25-29．

[6] 燕国材．非智力因素与学习（第二版）[M]．上海：上海教育出版社，2006．

[7] 李洪玉，阴国恩．中小学生学业成就与非智力因素的相关研究[J]．心理科学，1997，（5）：423-427，480．

[8] 张大均，刘衍玲．高中生心理素质与学业成绩的相关研究[J]．心理科学，2001，（1）：110-111．

[9] 沈烈敏，郭继东．影响学生学业成绩心理因素的研究[J]．心理科学，1999，（6）：559-560．

[10] 傅安球，李艳平，聂晶，等．关于动力系统中自我强化和学生期待对学习效率影响的实验研究[J]．心理科学，2002，（4）：425-428，510．

[11] 李新宇，李伟健．初中生数学成就动机与自我调节学习及学业成就之关系研究[J]．数学教育学报，2004，13（2）：52-54．

[12] Wechsler D. Cognitive, Conative and Non-Intellective Intelligence [J]. American Psychologist, 1950, (3): 78-83.

[13] Epstein S, Meier P. Constructive Thinking: A Broad Coping Variable with Specific Components [J]. Journal of Personality and Social Psychology, 1989, (2): 332-350.

[14] Tracey T J, Sedlacek W E. Non-Cognitive Variables in Predicting Academic Success by Race [EB/OL]. http://files. eric.ed.gov/fulltext/ED219012.pdf．

[15] Pintrich P R, Smith D A, Garcia T, et al．Reliability and Predictive Validity of the Motivated Strategies for Learning Questionnaire (MSLQ) [J]. Educational and Psychological Measurement, 1993, (53): 801-813.

[16] Pintrich P R. A Manual for the Use of the Motivated Strategies for Learning Questionnaire (MSLQ) [EB/OL]. http：//files.eric.ed.gov/fulltext/ED338122.pdf.

[17] Garcia T, McKeachie W J. The Making of the Motivated Strategies for Learning Questionnaire [J]. Educational Psychologist, 2005, (2): 117–128.

[18] 黄浦区“初中学生非智力心理因素的发展与教育”综合实验课题组，徐崇文．非智力心理因素的发展与教育综合实验报告（下）[J]．上海教育科研，1992，（2）：40-45．

[19] 洪德厚，周家骥，王养华，等．《中国少年非智力个性心理特征问卷》（CA—NPI）（1988年版）的编制与使用[J]．心理科学通讯，1989，（2）：15-19，66．

[20] 叶仁敏．中学生的成就动机，测验焦虑，智力水平与学业成绩关系的探讨[J]．应用心理学，1989，（3）：52-56．

[21] Richardson F C, Suinn R M. The Mathematics Anxiety Rating Scale: Psychometric Data [J]. Journal of Counseling Psychology, 1972, (6): 551-554.

[22] Carlson M P. The MathematicalBehavior of Six Successful Mathematics Graduate Students: Influences Leading to Mathematical Success[J]. Educational Studies in Mathematics, 1999, (3): 237-258.

[23] 侯杰泰，温忠麟，成子娟．结构方程模型及其应用[M]．北京：教育科学出版社，2004．

[24] 喻平．数学教学心理学[M]．北京：北京师范大学出版社，2010．

[25] 朱秉林，孔凡哲．数学学习动机[J]．数学教育学报，1992，1（1）：49-55．

[26] Davis L L. Instrument Review: Getting the Most from Your Panel of Experts [J]. Appl Nurs Res, 1992, (4): 194-197.

[27] Waltz C F, Strickland O, Lenz E R. Measurement in Nursing and Health Research [M]. New York：Springer, 2005．

[28] 王光明．数学教育需要重视的两个问题[J]．数学教育学报，2005，14（1）：31-34．

[29] 王光明，刁颖．高效数学学习的心理特征研究[J]．数学教育学报，2009，18（5）：51-56．

附录——数学学习非智力特征调查问卷

亲爱的同学：

你好！为了解高中生数学学习过程中的一些想法和感受，我们邀请你参与此次调查．首先感谢你的配合，请根据自己的实际情况，选出适合的答案，注意每个问题只能选一个答案．以下各题答案无好坏对错之分，回答结果只为科学研究所用，不作为其它依据．此次调查采取匿名做答，我们将对回答结果绝对保密，请务必认真、如实回答每一个问题，你的回答对我们的研究非常重要．

基本信息

学校：________班级：________性别：________年龄：________

1. 你的数学成绩在班级中通常是A名列前茅 B中上 C中等 D中下 E很差

2. 除去数学课上时间，你每天花在数学学习上的时间大约是A 3小时以上 B 2小时—3小时 C 1小时—至2小时D半小时—1小时 E半小时以下

3. 你认为影响数学学习成绩的最主要因素是A智力因素 B学习态度 C学习方法D学习兴趣 E数学教师或其他外在因素

4. 你的数学成绩经常在哪个分数段？（按百分制计算）A 90分以上 B 89.5—80分 C 79.5—70分 D69.5—60分 E 59.5分以下

调查项目

26 数学考试时遇到解不出的题目，我会紧张、发抖，或手出汗．27 与同学交流、讨论一些数学问题时，我很少反驳他们的观点．28 当学习任务中出现空间向量、圆锥曲线、三角函数等相关内容时，我会感到焦虑、情绪低落．29 对于均值不等式这样的公式，即使能很快记住，我也愿意自己推导一下．30 我会抓住机会学习一些教材之外的数学知识，即使那些未必能提高数学成绩．31 我喜欢听或者阅读关于数学文化、数学家、数学史等方面的奇闻逸事．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合32 数学考试前，我会担心、紧张得睡不踏实． A非常符合 B符合 C基本符合 D不符合 E非常不符合33 数学考试时，我总想着交卷时间很快就到了，出汗，影响思考．甚至会发抖、A非常符合 B符合 C基本符合 D不符合 E非常不符合34 钻研一些与数学有关的问题时，我经常会忘了时间． A非常符合 B符合 C基本符合 D不符合 E非常不符合35 如果高考不考数学，那么我就不用努力学习数学了． A非常符合 B符合 C基本符合 D不符合 E非常不符合36 为了提高或保持自己的数学成绩，我得努力学习数学．37 如果教师已经给出一道题的简便解法，我就不必继续寻更巧妙的方法了．找38 发现数学试卷上自己的正确答案被教师误判，我会十分愤怒，没有心情继续听讲．39 如果班上的数学教师教得不好、令人反感，我也就不想学习数学了．40 学习一些有难度的数学知识时，我担心自己学不会而逃避学习．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合41 当教师布置一些选作的数学题目时，我通常不理会． A非常符合 B符合 C基本符合 D不符合 E非常不符合42 如果需要我亲自计算生活中消费账单、银行存款利息、房贷款等问题时，我会紧张害怕，担心自己算错．住43 我认为数学知识是人们经过猜想、探究、推理、验证而得来的．44 数学学习中要做很多题，我会总结其中的技巧与规律，避免重复练习浪费时间．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合45 我对自己的数学学习有明确的计划，并命令自己执行． A非常符合 B符合 C基本符合 D不符合 E非常不符合46我总会为自己的数学学习感到担心、害怕，例如担心学内容太难而学不会、担心在数学课上出丑、担心考试失败习A非常符合 B符合 C基本符合 D不符合 E非常不符合等．47 对于一些数学符号或公式，例如log、f(x)等，我会感到困难，担心自己不能理解．A非常符合 B符合 C基本符合 D不符合 E非常不符合48 学习立体几何时，我认为有没有必要花时间来学习证明步骤，那只是繁琐的形式． A非常符合 B符合 C基本符合 D不符合 E非常不符合49 我认为数学公式是可以随意应用、无需质疑和检验的真理．A非常符合 B符合 C基本符合 D不符合 E非常不符合50 向教师或同学请教一些自己不能理解的内容或试题，代表着我数学不好．51 即使数学教师的教学非常枯燥，不合我的胃口，我也能坚持听讲，并努力理解．52 与班里大部分同学相比，我确信自己在数学方面有出色的能力．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合53 教师要求我回答问题或上台板演时，我一般都有信心答对．A非常符合 B符合 C基本符合 D不符合 E非常不符合54 无论对三角函数这部分的知识有无兴趣，我都要努力地学习这部分内容．A非常符合 B符合 C基本符合 D不符合 E非常不符合55 在数学课堂上，我不能表现得比其他同学差． A非常符合 B符合 C基本符合 D不符合 E非常不符合56 在数学学习方面，我相信“有志者事竟成”，并句话激励自己．经常用这A非常符合 B符合 C基本符合 D不符合 E非常不符合57 我认为网上的一些解题方案或技巧，直接引用即可． A非常符合 B符合 C基本符合 D不符合 E非常不符合

58 教师要求小组合作、共同探究一些数学问题时，我希望独完成其中最重要的一部分．单59 从高中数学的难度、教师和自我能力等方面综合考虑，我相信自己能出色地完成数学课程的学习．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合60 教师给出的结论或公式，一定是对的，可以直接使用． A非常符合 B符合 C基本符合 D不符合 E非常不符合61 我认为学生数学成绩不好，主要是教师教学能力差． A非常符合 B符合 C基本符合 D不符合 E非常不符合62 我相信我能够掌握高中数学中最难的那一部分知识． A非常符合 B符合 C基本符合 D不符合 E非常不符合63 遇到那些比我的数学成绩好的同学，我会不自觉地找他（她）身上的缺点． A非常符合 B符合 C基本符合 D不符合 E非常不符合64 学生都是爱玩的，所以不必责怪自己因为贪玩而影响了数学学习．A非常符合 B符合 C基本符合 D不符合 E非常不符合65 当我的答案与练习册上答案不一致时，我会再次认真演算．A非常符合 B符合 C基本符合 D不符合 E非常不符合66 我认为数学教材除了印刷错误，不会再有其他的错误． A非常符合 B符合 C基本符合 D不符合 E非常不符合67 解数学题时，如果我与多数人的答案不一样，我会放弃己的答案．自68 函数、导数、二面角、空间向量等概念的学习，对我来说都不成问题．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合69 对于感到困惑的公式或定理，我会主动向教师询问． A非常符合 B符合 C基本符合 D不符合 E非常不符合70 即便我付出足够的努力，我也不会在数学上取得出色的就．成71 数学考试后，我对全班最好的成绩是多少分、是谁取得的特别感兴趣．72 如果面向全班同学讲解自己的解题思路，受到质疑时我会据理力争．73 我认为学生数学成绩的高低，主要取决于自身的学习态度、努力程度等．74 对于一些数学符号或公式，例如log、f(x)等，我感到容易，都能够理解．75 对于数学试卷上的错题，我会认真改正，并提醒自己不要再犯同样的错误．76 如果最近两次数学考试成绩都不理想，我会觉得我不适合学习数学，趁早把精力转移到其他科目上．77 数学解题过程中，如果我的解法经常失败，说明我在数学上无能．78 我给自己定下的数学学习计划，经常因为坚持不下来而泡汤．79 没有超常的智力，我也有信心学好高中阶段的数学，甚至高等数学．80 数学作业的答案正确就可以，解题过程、工整的字迹都无关紧要．81 如果家长或学校能用一些奖品、奖金……来奖励我的数学学习，我会更愿意学数学．A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合A非常符合 B符合 C基本符合 D不符合 E非常不符合82 与同学交流、讨论一些数学题时，我很少反驳他们的观点．A非常符合 B符合 C基本符合 D不符合 E非常不符合

因题目较多，请再检查一遍是否有遗漏的题目．非常感谢你的配合，祝你学习进步！

[责任编校：周学智]

Compilation of Non-Intellective Characteristics Questionnaire for High School Students’ Mathematics Learning

WANG Guang-ming1, SONG Jin-jin1, WANG Zhao-yun2
(1. College of Teacher Education, Tianjin Normal University, Tianjin 300387, China; 2. Ontario Institute for Studies of Education, University of Toronto, Toronto, Canada)

Educators should pay close attention to students’ mathematics learning activities. The non-intellective factors in the questionnaire is closely related to the high school students’ mathematics learning, it can be used as tool for investigation and evaluation non-intellective psychological characteristics of high school students’ mathematics learning. This study try to construct a survey model of the non-intellective characteristics in math learning by sorting the relevant literature and combined with expert opinion at home and abroad. Then compiled items suitable for high school students’ math learning on the basis of the survey model. After revised several times, the results show that the questionnaire has a reasonable structure, reliability and validity meet the psychometric requirements. Non-intellective Characteristics Questionnaire for High School Students’ Mathematics Learning can be used as a tool for further research.

non-intellective factors; mathematics learning; compilation of questionnaire

G420

：A

：1004–9894（2015）03–0017–11

2015–05–19

教育部人文社科一般项目——高中生高效学习的心理特征研究（13YJA190012）；天津市高校“中青年骨干创新人才培养计划”资助

：王光明（1969—），男，天津人，教授，博士生导师，主要从事数学课程与教学论研究．