船桥撞击力理论公式与数值模拟对比研究
2020-07-06温永华
邓 超 温永华 吴 琼
(江西交通职业技术学院,南昌 330013)
0 引言
随着我国水上运输业的高速发展, 跨航道桥梁数量与日俱增,船舶撞击桥墩的概率大大的被提升。与此同时,船运流量、吨位和速度等也在逐年增加。船舶撞击桥墩事故的发生,轻则导致桥墩结构损伤,重则造成桥梁倒塌。据不完全统计, 全世界平均每年发生1 起船桥相撞事故,约有10%的桥梁因船舶撞击而倒塌[1]。为保证大桥桥墩能够承受航道内大型船舶的意外撞击, 在桥墩设计中需考虑一个关键因素——船桥撞击力。 目前,国内外船桥撞击力的理论公式众多, 其核心大多只考虑船舶航行质量与撞击速度,对其它因素(水流作用等)涉及较少,且各规理论公式都是对船桥撞击力进行一个估算, 与真实情况下的船桥撞击力结果还是存在一定的差异。 随着撞击理论不断完善及有限元软件的快速发展, 数值模拟成为模拟船桥撞击过程的一个重要手段, 其能够较为真实的反映船桥撞击过程每个阶段的船桥撞击力情况。
对于船桥撞击问题,林建筑等[2]以后渚大桥为背景,通过缩尺模型试验对船桥撞击力进行研究。 对比发现,美国AASHTO 规范的设计船桥撞击力与试验结果最为接近,而中国现行规范规定的设计船桥撞击力数值则明显偏低。 胡志强等[3]利用有限元模拟仿真,模拟了在刚性墩上船舶的正向冲击过程,得到船桥撞击力的时程曲线、撞击能量深度时程曲线和撞击深度时程曲线的相关数据。Consolazio 等[4]提出了一种有效的数值计算方法来分析不同船舶碰撞下的桥墩动响应问题, 其中综合考虑了船舶质量、撞击速度等参数的影响,并通过该数值计算方法与LS-DYNA 计算结果所用机时的对比,证明该数值计算方法能大大减少碰撞计算的时间。罗林阁等[5]通过冲击动力学理论,应用LS-DYNA3D 通用程序对船舶撞击力进行数值计算,将分析结果与公路规范公式进行对比,归纳一个可供工程设计选用修正系数表。 熊安平等[6]利用LSDYNA 仿真模拟探索船舶刚度对船桥撞击力的影响,得出船桥撞击力与船舶刚度成一次线性关系, 并且其斜率接近0.5 这一结论。 潘晋等[7]建立散货船与桥墩的撞击模型, 通过分析发现铁路桥涵设计规范的船桥碰撞力公式更适合于斜艏500 t 至3 000 t 级散货船, 而美国公路桥梁设计规范的船桥撞击力理论公式对该类型吨级船舶的碰撞力结果偏大。 文传勇[8]基于有限元分析,得出了万州长江大桥桥墩可承受极限撞击船舶吨位为115 t。 宗莉娜等[9]通过数值模拟对船舶撞击刚性墙的船舶速度、吨位、接触面积对船桥撞击力大小的影响进行研究,结果发现,最大撞击力与撞击速度近似成正比,与船舶吨位无线性关系,与接触面积成正比。同样地,陈涛等发现撞击力与船舶吨位的平方根近似成线性关系, 与撞击速度近似成线性关系;随着撞击角度增大,撞击力减小,撞击时长增加。 张哲等[10]对船桥碰撞进行有限元模拟,并将结果与动力数值模拟结果相比, 发现利用有限元模拟较动力数值模拟进行船桥碰撞分析准确性更高。
本文基于ANSYS/LS-DYNA 软件平台建立船桥撞击过程有限元模型, 研究船舶航行质量和撞击速度两因素对船桥撞击力的影响, 并将所得结果与理论公式计算结果进行对比分析, 选出适用于该水域船桥碰撞力设计的理论公式,同时为相应的桥梁防船撞设计提供参考。
1 船桥撞击力理论公式
1.1 《公路桥涵设计通用规范》公式[11]
该规范指出四至七级内河航道缺乏实际调查资料时,可以参照当前规范选取撞击力设计值,并给出了船舶撞击力理论公式,该公式目前只适用于内河船舶,即船舶吨级在3000t 以下。 其理论公式如下:

式中,P 为撞击力,kN;W 为船舶航行质量,kN;v 为船舶撞击速度,m/s;g 为重力加速度, 取g=9.8m/s2;T 为撞击时间,应根据实际资料估计,在无实际资料时,取T=1s。
1.2 《铁路桥涵设计基本规范》公式[12]
该规范指出,撞击力的作用高度,应根据具体情况确定,缺乏资料时可采用通航水位的高度。在计算时,将船桥撞击力纳入特殊荷载中,并采用静力法假设,即假定船舶作用在桥墩上的有效动能全部转化为撞击力所做的静力功。 其理论公式如下:

式中,F为撞击力,kN;γ 为动能折减系数,s/m1/2,当斜向撞击时,取γ=0.2;当正向撞击时,取γ=0.3;v 为船舶撞击速度,m/s;α 为船舶行驶方向与墩台撞击点处切线所成的夹角,应根据具体情况确定,本文采用正向撞击,取α=90°;w 为船舶航行质量,kN;C1、C2分别为船舶弹性变形系数和墩台圬工的弹性变形系数,当缺乏资料时,可假定C1+C2=5×10-4m/kN。
1.3 Woisin 理论公式
通过散货船撞击刚性桥墩实验,Woisin 发现船舶撞击刚性墙产生的最大撞击力出现在撞击过程的0.1 至0.2s 之间,并提出了沃辛公式,其理论公式如下:

在考虑了撞击速度为撞击力影响因素后,Saul 与Svensson 对沃辛公式进行修正,得到公式[14]:
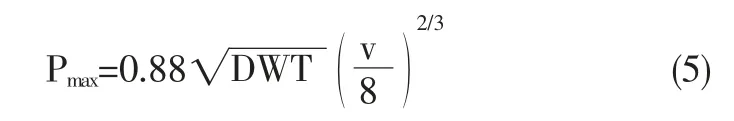
式中,Pmax为船桥撞击时产生的最大撞击力,MN;DWT为船舶的载重吨位,t;v 为船舶撞击速度,m/s;Pm为平均撞击力,MN。
1.4 AASHTO 规范公式[15]
AASHTO 认为参照Woisin 理论公式计算的撞击力存在70%的误差,于是将系数从0.88 改成0.98,同时增加了撞击速度因子。 其理论公式如下:
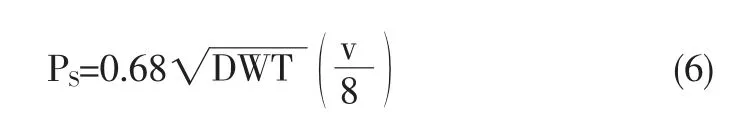
式中,PS为船舶静态等效撞击力,MN;DWT 为船舶的载重吨位,t;v 为船舶撞击速度,m/s。
1.5 欧洲规范公式[16]
1999 年欧洲出版统一规范, 指出在计算船桥撞击力时,船艏采用准弹性单自由度模拟,并假设桥墩为刚性,而且不产生位移。 其理论公式如下:

式中,F 为船桥撞击时的撞击力,MN;v 为船舶撞击速度,m/s;K 为船舶的等效刚度,MN/m,对于处于内河内的船舶, 取v=3m/s,K=5MN/m; 对于远洋船舶, 取v=3m/s,F=15MN/m;M 为船舶航行质量,t。
1.6 撞击力理论公式的对比
对各撞击力理论公式计算结果进行对比, 为桥梁设计找到一种既安全又合理的船桥撞击力理论公式。 在本节中,变量控制为船舶航行质量和撞击速度。情况一,研究在船舶航行质量为1000t 时, 计算船舶撞击速度分别为3m/s、4m/s、5m/s、6m/s 下的船桥撞击力;情况二,研究在船舶撞击速度为5m/s 时, 计算船舶航行质量分别为500t、1000t、2000t、3000t 下的船桥撞击力。 将以上两种情况下的各撞击力理论公式计算结果汇总,分别得到表1 和表2。
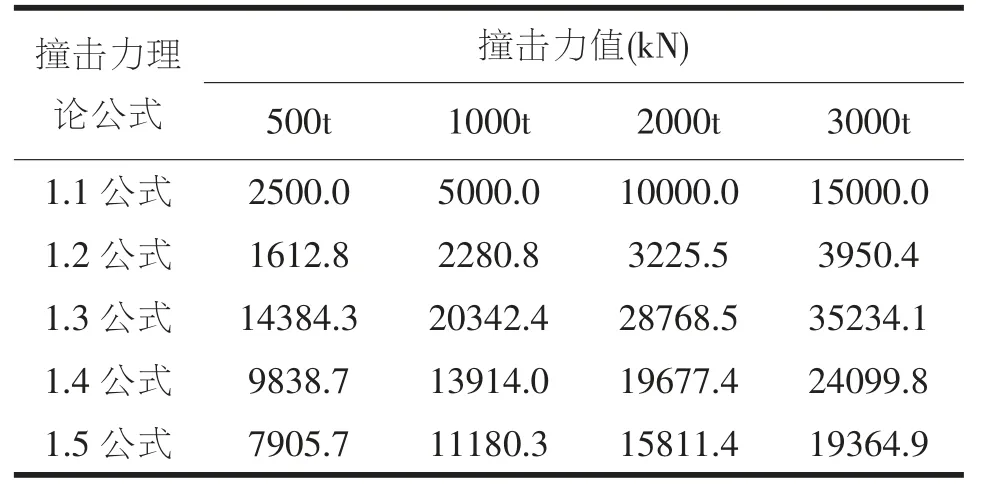
表1 不同船舶航行质量下各撞击力理论公式计算值
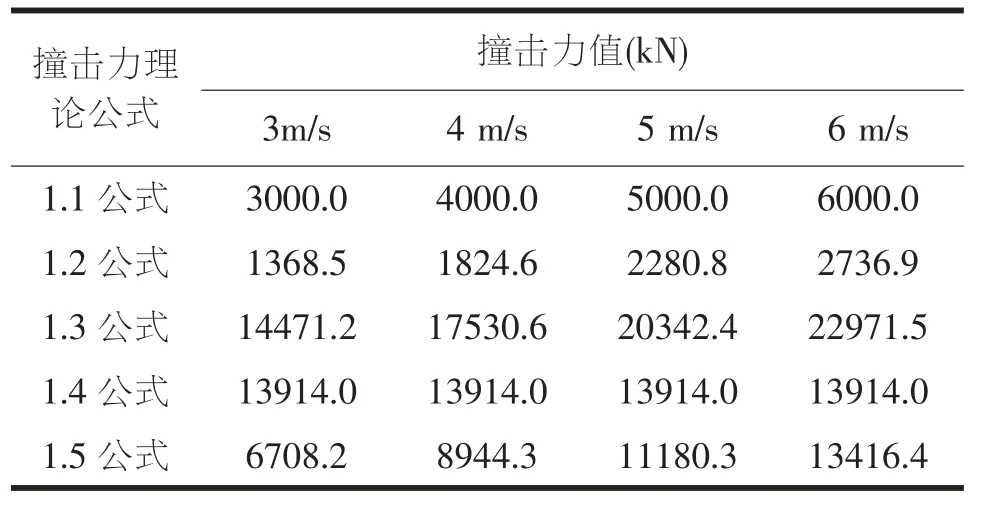
表2 不同船舶撞击速度下各撞击力理论公式计算值
从表1 及表2 可以得出,1.3 公式考虑的情况为船舶撞击刚性桥墩,其所计算的撞击力值过于偏大。 在其它四个公式中,1.4 公式所计算出来的撞击力数值最大,分别为表1 中DWT=1000t,v=6m/s 时的情况和表2 中DWT=3000t,v=5m/s 时的情况, 此时, 船桥撞击力最大值分别为13914.0kN 和24099.8kN;而对于1.2 公式,即我国《铁路桥涵设计基本规范》,在表1 及表2 呈现的船桥撞击力值都为最小。所以相对于而言,依照美国AASHTO 规范中考虑船桥撞击力理论计算值来设计桥梁是更为安全的。
2 船桥撞击数值模拟
2.1 有限元模型
桥梁下部结构选用赣江流域某一跨江铁路桥墩进行建模,桥墩为花瓶式Y 型墩,考虑船舶正面撞击桥墩。 桥墩模型采用SOLID164 实体单元, 共包含21200 个单元,23814 个节点,桥墩底部采用刚性固定,桥墩有限元模型见图1。

图1 桥墩有限元模型
船舶原型参考某3000 DWT 散货船的实际形状和尺寸, 其最大载重量为3850t, 满足本文模拟的最大吨级为3000t 的情况,船舶的主要部位尺寸数据见表3。船舶模型采用SHELL163 壳单元,共包括了39503 个单元,39542 个节点。 船舶有限元模型见图2。

表3 船舶主要部位尺寸表

图2 船舶有限元模型
2.2 材料模型
桥墩采用C40 混凝土,处理为弹性材料,材料相关参数如下:密度ρ=2.4g/cm3,抗压强度fc=48MPa,泊松比v=0.3,弹性模量E=35.7GPa。 船舶采用Q235 钢材,处理为弹塑性材料,材料相关参数如下:密度ρ=7.85g/cm3,弹性模量E=260GPa,泊松比v=0.3,屈服强度fy=235MPa,硬化模量Eh=1.18×103MPa,抗拉强度fu=370MPa。
船桥撞击过程是一个动态响应过程, 材料的动力特性影响不能忽略。 在撞击过程中船艏会出现严重的变形,同时船用材料低碳钢塑性性能对应变率是极其敏感的,其屈服和拉伸极限与应变率成正比,因此本文采用Cowper-Symonds 本构方程来解决应变率敏感性问题[7]。

式中,ε 为塑性应变率;σ0′和σ0分别为在塑性应变率时的动屈服应力和静屈服应力;C 和p 为材料常数, 对船用钢,取C=40.4 和p=5。 材料的失效非常复杂,可通过最大塑性失效应变来定义材料的失效, 即当结构单元的等效塑性应变达到定义的单元最大塑性失效应变时, 单元失效,失效后的单元将不再参与后面的计算。 根据所建立模型的单元大小,取材料的最大塑性失效应变为0.35。
2.3 载荷及边界条件
船桥撞击过程中船舶主要做纵荡运动, 采用附连水质量系数0.07 来计入周围流体的作用[17]。 不约束船体的转动与平动自由度,并施加初始速度。
3 结果分析
3.1 船舶航行质量对撞击力的影响
我国内河航道船舶的最大吨位为3000t,因此在本小节中,模拟研究中控制船舶撞击速度为5m/s,航行质量分别为500t、1000t、2000t、3000t 的船舶与桥墩发生正面(即夹角为90°)撞击,图3 为不同船舶航行质量下的撞击力时程曲线。
由图3 可知,船舶撞击速度相同时,不同船舶航行质量下的撞击力随时间变化趋势大致相同, 表明船桥撞击力与船舶航行质量成正比关系。 整个船舶撞击桥墩过程极短,只有在同一时刻撞击力值不相等,随着撞击时刻不同,撞击力值开始是快速增长,然后缓慢增长一段时间,最后船桥分离,撞击力值变为零。 当船舶速度为5m/s,航行质量分别为500t、1000t、2000t、3000t 时,撞击桥墩产生的最大撞击力值分别为2MN、4.2MN、7.1MN 和11.1MN。

图3 不同船舶航行质量下的撞击力时程曲线
3.2 船舶撞击速度对撞击力的影响
我国内河航道船舶的航速一般为15 节至18 节。 在本节中,取航速为15 节,换算成国际单位就是7.72m/s,因此本节研究的船舶撞击速度最大为6m/s 是合理的。 在不考虑其它因素的影响,模拟船舶航行质量为1000t 下的撞击速度分别为3m/s、4m/s、5m/s 和6m/s 的船桥正面撞击过程。

图4 不同船舶撞击速度下的撞击力时程曲线
分析图4 可知, 不同船舶撞击速度下的撞击力时程曲线趋势完全一致, 表明船桥撞击力与撞击速度成正比关系。在同一时刻撞击力值不相等,随着撞击时刻不同,撞击力值开始是快速增长,然后缓慢增长一段时间,最后撞击力值变为零。 到达撞击力峰值的时间为0.6s,撞击力最大值为5.83MN。 当船舶质量为1000t, 撞击速度分别为3m/s、4m/s、5m/s、6m/s 和7m/s 时,撞击桥墩产生的最大撞击力值分别为2.4MN、3.3MN、4.2MN、5.0MN 和5.8MN。
3.3 有限元模拟结果与撞击力理论公式的对比
通过将有限元数值仿真得出的撞击力值与各国规范理论公式得出的撞击力值进行对比分析, 为桥梁设计找到一种既安全又合理的理论公式。
表4 和表5 分别为不同情况下的船桥撞击力理论公式计算值与数值模拟值的对比汇总。 由表可知,1.2 公式计算的不同状况下的撞击力值均小于有限元数值仿真结果得出的不同状况下的撞击力值; 而有限元数值仿真结果得出的不同状况下的撞击力值均小于1.1 公式、1.3 公式、1.4 公式及1.5 公式在不同状况下计算得出的撞击力值, 而且与1.1 公式计算的撞击力值最为接近,1.3 公式、1.4 公式及1.5 公式计算得出的撞击力值相对于有限元分析结果得出的撞击力值都过于偏大。 综上所述,在设计跨河、跨海桥梁时,参考1.1 公式计算的撞击力值来设计桥梁是最为适宜的。

表4 不同航行质量下的各撞击力公式计算值
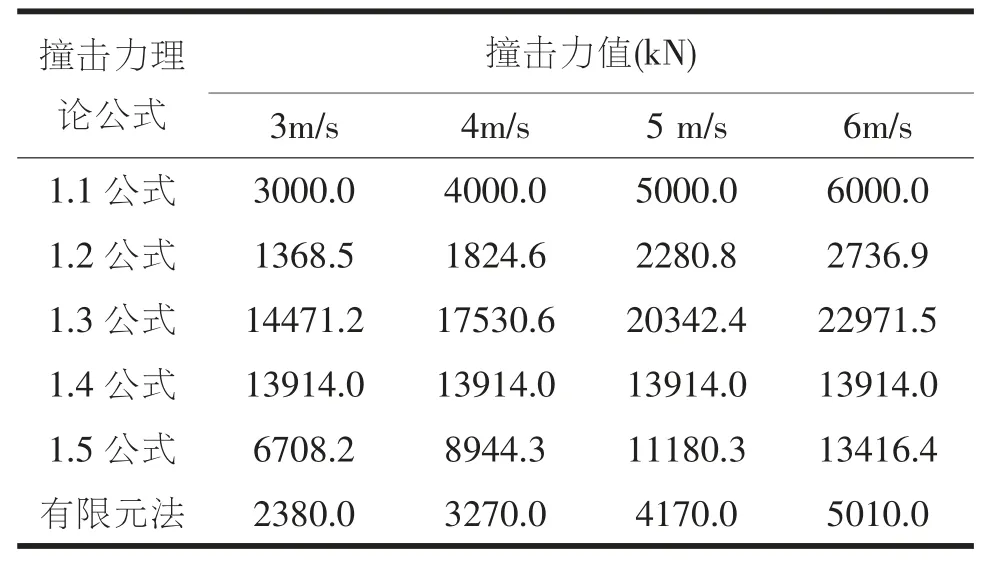
表5 不同撞击速度下的各撞击力公式计算值
4 结论
通过有限元软件对船舶航行质量和撞击速度这两个变量下的船桥撞击过程进行数值模拟, 并将有限元数值模拟得出的撞击力值和几种经典理论公式得出的撞击力值进行对比分析,得出以下结论:
(1)船桥撞击过程是瞬间发生的,撞击力在极短时间内先快速增加,然后缓慢增长一段时间,最后撞击力值快速的变为零。 因此,船桥撞击过程能量之间的转换也是极为快速的。
(2)通过考虑船舶航行质量和船舶撞击速度这两个因素的影响, 将不同状况下的有限元数值仿真得出的撞击力值与各个理论公式得出的撞击力值进行对比分析,发现我国《公路桥涵设计通用规范》计算的撞击力值与有限元数值仿真得出的撞击力值最为接近。 同时,当船舶航行质量与撞击速度分别为定值时, 船桥撞击力结果曲线变化趋势相同,这更好的验证了我国《公路桥涵设计通用规范》公式的正确性。因此,在设计跨河、跨海桥梁时,参考我国《公路桥涵设计通用规范》公式计算的撞击力值来设计桥梁是最为适宜的。
