考虑横竖向车桥耦合曲线桥的动力响应影响
2020-08-03许汉铮商朋朋李晓涛陈武浩
许汉铮, 潘 宏, 商朋朋, 李晓涛, 陈武浩, 胡 眺
(1.长安大学公路学院,西安 710054;2.浙江省绍兴市公路管理局,绍兴 312000)
当车辆行驶在桥梁上,曲线桥会产生一定的动力响应[1],分析汽车荷载作用下结构的动力响应必须考虑车桥耦合作用[2],而现有的研究成果很少考虑横向车桥耦合作用。但如果不考虑横向耦合振动或者对横向耦合振动考虑欠佳,都会对真实的车桥耦合振动分析产生一定的偏差,通过对混凝土连续曲线桥在有无横竖向车桥耦合作用下的动力响应对比分析,更加清晰认识混凝土连续曲线桥的动力响应,为保证桥梁运营期间的安全、延长使用寿命、减少经济损失等方面具有重要意义。
目前,中外学者在车桥耦合方面的研究较多:李清海等[3]通过考虑多轴及多个车辆的作用于多种支承条件下的桥梁,采用三次插值函数建立桥梁相关运动方程,并引入超单元法建立了车辆荷载运动方程,分析桥梁结构的振动响应;周乐[4]通过建立分离的7个自由度两轴整车模型和连续曲线梁模型振动方程,运用接触处的位移协调条件,推导耦合系统运动方程,并以实际曲线梁桥为背景,分析单车荷载作用下曲线梁桥横竖向耦合振动响应的影响;Marchesiello等[5]建立七自由度系统3轴汽车模型,以恒定速度过桥,对一座三跨桥梁进行了数值分析,研究桥梁扭转模态形状的动力响应;Willis[6]不考虑桥梁本身的自重,通过建立车桥耦合振动方程,得出了近似的解析解,研究发现静力作用下桥梁的应力和变形均小于动力作用桥梁的应力和变形。然而针对车桥耦合振动的研究大都集中于竖向的振动问题,对横向耦合振动问题研究较少涉及。
为此,在竖向车桥耦合作用的基础上进一步考虑横向车桥耦合的混凝土曲线桥动力响应,以期得到混凝土曲线桥横向位移的精确解,为防治混凝土曲线桥的横向爬移病害提供参考依据。
1 曲线桥模型
1.1 曲线桥概况
以3 m×25 m的混凝土连续曲线桥作为研究对象,并建立相应的有限元模型。曲线桥为单箱单室截面,桥梁中心线位于80.25 m的圆曲线上,该箱梁顶板宽度和厚度分别为8.5、0.25 m,底板宽度和厚度分别为4.5、0.2 m,腹板厚度为0.5 m,两侧悬臂板长度均为2 m,悬臂板端部厚度0.2 m,根部厚度0.4 m,由端部向根部按线性渐变。横断面如图1所示。
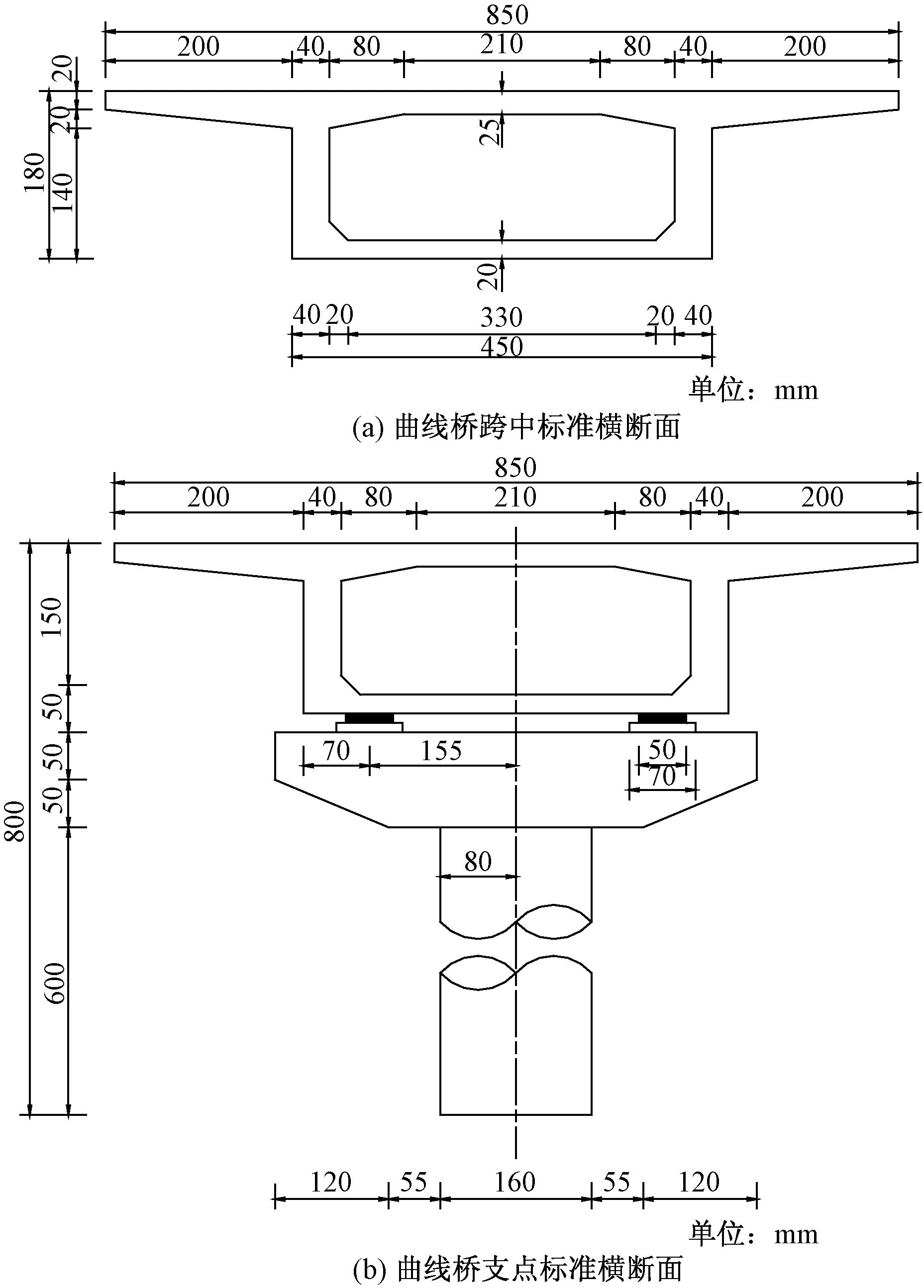
图1 曲线桥跨中、支点标准横断面图Fig.1 Standard cross section diagram of mid-span and fulcrum of curved bridge
1.2 有限元模型
通过有限元软件ANSYS,建立曲线梁桥模型,同时划分单元网格,主梁部分采用3D实体单元solid65,选用的材料参数为弹性模量3.45×104MPa,材料密度为2 600 kg/m3,泊松比0.2;针对盖梁、支座垫石和桥墩,采用与主梁相同的参数建立模型,曲线桥有限元模型如图2所示。

图2 曲线桥实体单元模型Fig.2 Solid element model of curved bridge
2 耦合振动整车模型
2.1 车辆系统构成
车辆是由轮胎、悬架、车体等相关元件所组成,各个元件在空间上存在6个自由度,因各个部件沿着行车方向产生伸缩对研究横向和竖向的车桥耦合效应几乎没有影响,因此各刚体的伸缩位移可以忽略,这样,针对每个刚体,在运动过程中可以只考虑5个自由度[7],即横移、侧滚、浮沉、摇头及点头。为了更能真实地反映汽车在桥面上行驶的动态过程,拟采用三轴车辆(双后轴)模型,分成7个刚体,即6个车轮和1个车体,整个车辆自由度为17[8],其立面及侧面如图3所示。

图3 三轴车辆模型示意图Fig.3 Schematic diagram of three-axle vehicle model
2.2 车辆参数
为了更能真实地反映汽车在桥面上行驶的动态过程,拟采用三轴自卸汽车的相关参数对车辆建立参数化模型[9-11],车身质量为28 500 kg,其车辆技术参数见表1。

表1 车辆技术参数
2.3 耦合系统动力学方程的建立与求解
根据桥梁结构的运动方程组和结构阻尼矩阵可推导出车桥耦合系统的运动方程组,车桥两个子系统表达式为
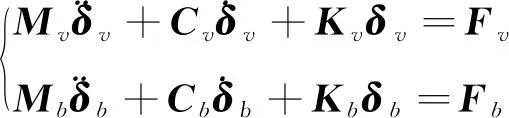
(1)
式(1)中:Mv、Mb、Cv、Cb、Kv、Kb分别为桥梁和车辆的质量、阻尼和刚度矩阵;因此可以用式(2)表示:

(2)
式(2)中:Fv、Fb分别为桥梁和车辆的整体外力向量,Fb与车辆和桥梁的运动有关,Fv只与路面不平度和桥梁的运动有关;δv、δb分别代表桥梁、车辆的自由度向量;i为路面粗糙度。
车辆系统与桥梁系统接触处的几何相容条件可以表示为
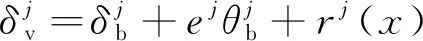
(3)

车与桥在接触处的平衡条件可表示为
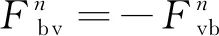
(4)
3 横竖向车桥耦合曲线桥动力响应
3.1 动力特性分析
运用ANSYS对混凝土连续曲线桥进行模态分析,得到背景桥梁的振动特性,对前6阶的自振频率进行汇总,如表2所示:
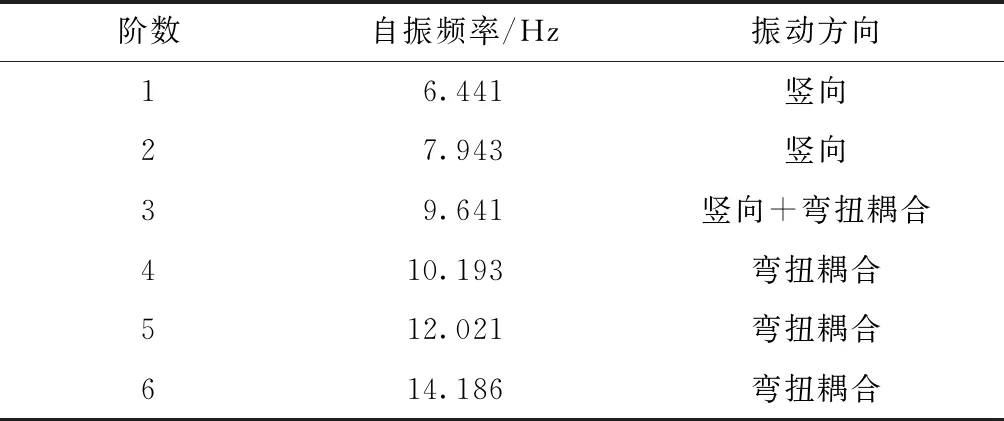
表2 曲线桥模态分析
由表2可知,一阶二阶振型以竖向振动为主,三阶振型除了竖向振动以外,还会伴随着轻微的侧向的弯扭耦合振动,而高阶振型,弯扭耦合振动效应明显,与曲线桥的实际动力特性相符。
3.2 不考虑横竖向车桥耦合
3.2.1 曲线桥横向力
在不考虑横竖向车桥耦合作用时,分别采用10、30、50、70 t车重,并以50 km/h的速度上桥。通过运行分析,对不同车重情况下曲线桥跨中截面处沿半径方向的力进行分析,因研究对象为3 m×25 m 的混凝土连续曲线桥,即对1#跨中截面、2#跨中截面、3#跨中截面处的横向力进行分析,其时程曲线如图4所示。

图4 曲线桥跨中横向力时程曲线Fig.4 Time-history curve of transverse force in mid-span of curved bridge
由图4可以得到如下结论:当车辆接近1#、2#、3#跨跨中时,曲线桥横向力会逐渐变大。当车辆经过跨中时,横向力产生突变,因为车辆为三轴车,质量集中在三个轴处,所以突变会发生三次。
当汽车后轴驶离跨中截面处,曲线桥横向力达到反向最大值,车辆驶离曲线桥,横向力逐渐变小。整个过程不涉及车桥耦合作用,所以曲线桥横向力时程曲线比较圆滑,无波动产生。不同车重汽车上桥,横向力的最大值明显增大,说明车重对曲线桥的横向力影响显著。为了进一步确定车重对横向力的影响,对不同车重下各跨中截面横向力的最大值进行汇总,其跨中截面横向力最大值如表3所示。
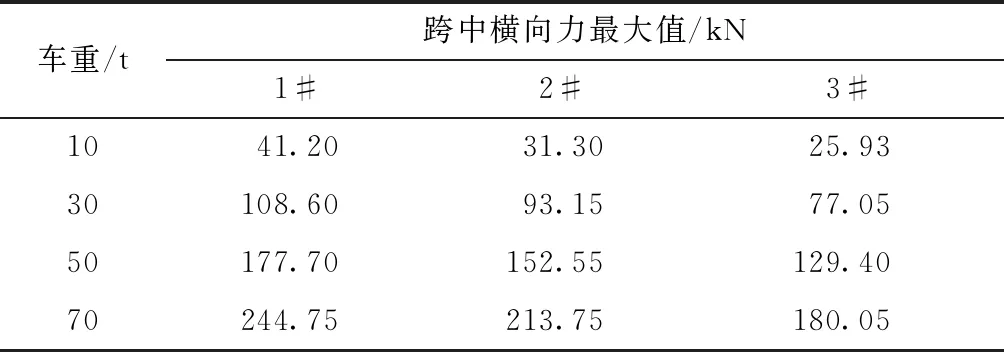
表3 跨中横向力最大值
由表3可知,随着车重增加,相同跨跨中横向力最大值逐渐增加,70 t车重作用下,1#跨中截面横向力最大值能达到244.75 kN,同一车重下,不同跨中截面产生的横向力不同,其中1#跨中截面产生的横向力高于其他截面。
3.2.2 曲线桥横向位移
为了更加明确曲线桥真实变化情况,提取跨中截面横向位移,绘制相关时程曲线,如图5所示。
由图5可以得到如下结论:不同车重汽车上桥,曲线桥跨中截面横向位移变化趋势相同,都逐渐增大,随着车重的增加,曲线切线斜率越大,说明车重对曲线桥跨中截面横向位移影响明显。1#跨中截面横桥向位移随着汽车三个轴依次上桥而逐渐增大,0.5 s后,车辆后轴驶入桥面,时程曲线不再有波动,1.2 s左右,车辆中心穿过1#梁跨中截面,其横桥向位移达到峰值,之后逐渐减小。对于2#跨中截面,当时间达到2.8 s左右时,此时汽车驶入跨中截面处,其横向位移达到峰值。3#跨中截面横向位移与1#跨中截面具有对称的变化趋势。
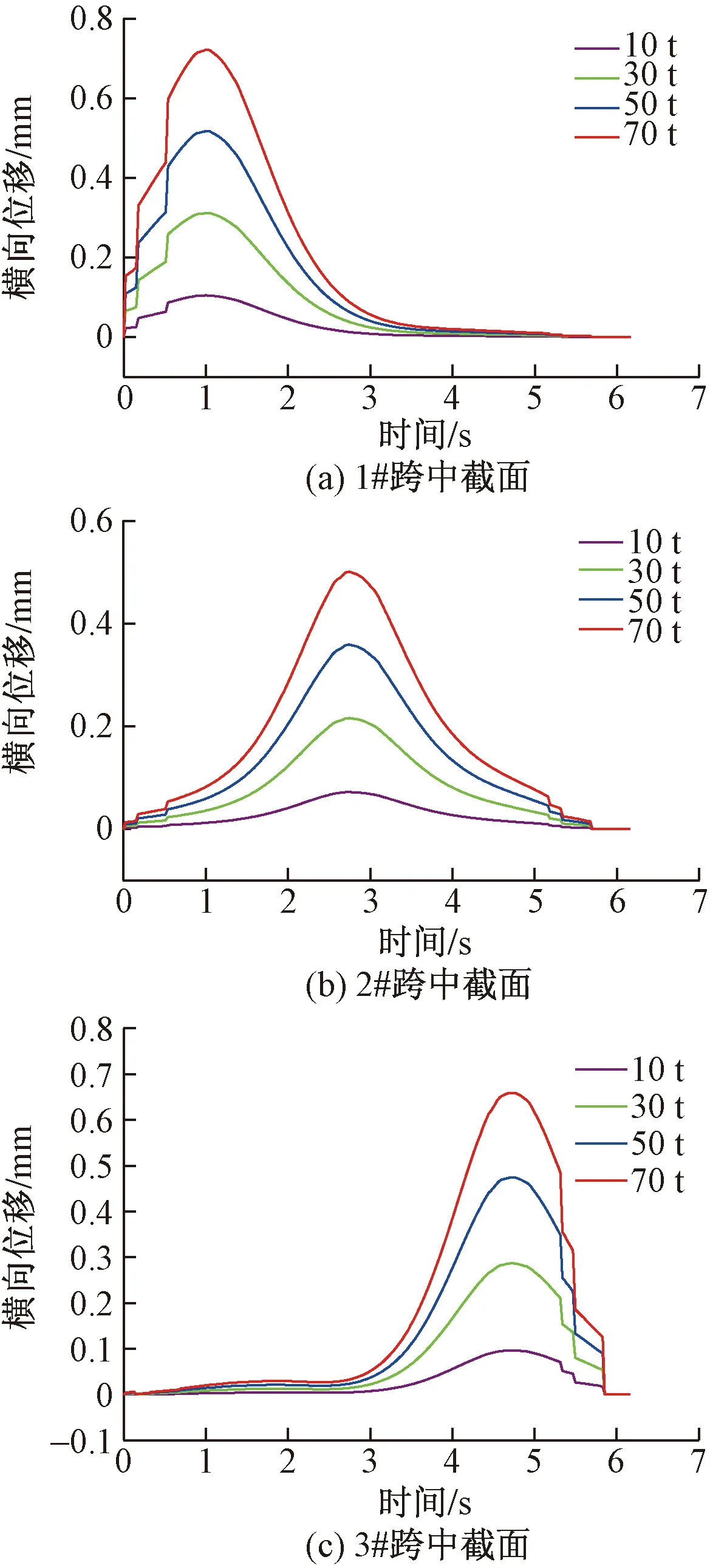
图5 曲线桥跨中横向位移时程曲线Fig.5 Time-history curve of lateral displacement in mid-span of curved bridge
为了进一步确定车重对横向位移的影响,对不同车重下各跨中截面横向位移的最大值进行汇总,其跨中截面横向位移最大值如表4所示。
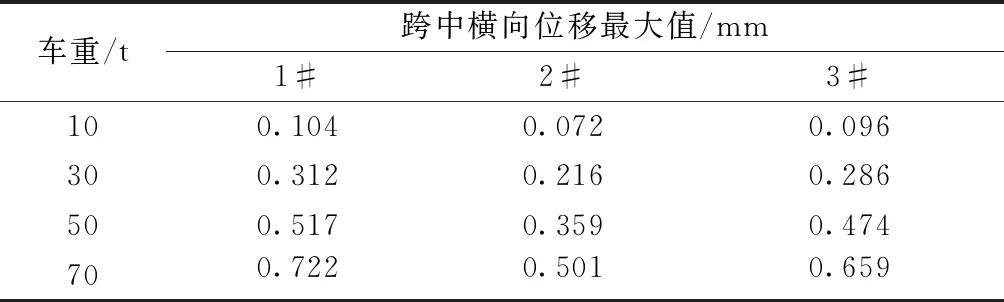
表4 跨中横向位移最大值
由表4可知,随车重增加,所有跨中截面的横向最大位移值逐渐变大;同一车重下,位于边跨的截面产生的横向位移大于中跨截面,70 t车重作用下,1#跨中截面横向位移最大能达到0.722 mm。
3.3 考虑横竖向车桥耦合
3.3.1 曲线桥横向力
在考虑横竖向车桥耦合作用的情况下,分别采用10、30、50、70 t的车重,以50 km/h的速度上桥,通过对车桥耦合作用不同车重汽车上桥进行分析,提取曲线桥跨中截面处沿半径方向的力,其时程曲线如图6所示。
由图6可以得到如下结论:横竖向车桥耦合作用下,不同车重的跨中横向力时程曲线变化趋势总体不变。当车辆接近1#、2#、3#跨跨中时,曲线桥横向力会逐渐变大,因为考虑到横竖向车桥耦合作用,横向力的变化曲线会产生波动性。当车辆经过跨中时,横向力产生突变,变化趋势与不考虑车桥耦合作用一致。车辆驶离曲线桥,横向力逐渐变小,曲线桥横向力时程曲线会随之产生一定的波动,且逐渐减小。为了进一步确定车重对横向力的影响,对不同车重下各跨中截面横向力的最大值进行汇总,其跨中截面横向力最大值如表5所示。
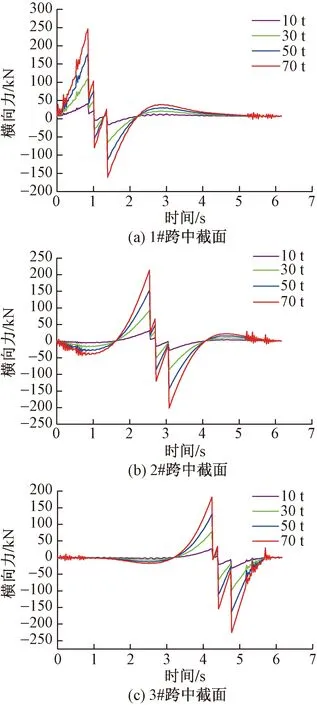
图6 曲线桥跨中横向力时程曲线Fig.6 Time-history curve of transverse force in mid-span of curved bridge
由表5可知,相同跨跨中横向力最大值随车重变化与不考虑车桥耦合效应一致,即都逐渐增加。70 t车重作用下,同一车重1#跨中截面横向力最大值大于其他截面,说明车重增加曲线桥横向受力越不利,1#跨中截面横向力最大值能达到248.25 kN。
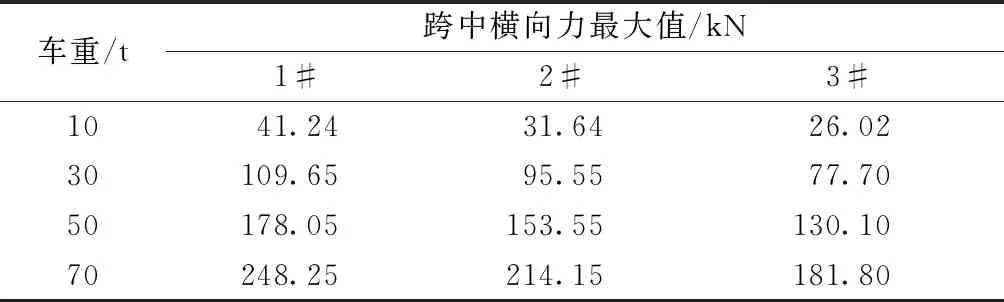
表5 跨中横向力最大值
综上所述,是否考虑横竖向车桥耦合作用,对曲线桥的横向力进行对比分析,绘制柱状图,如图7所示。
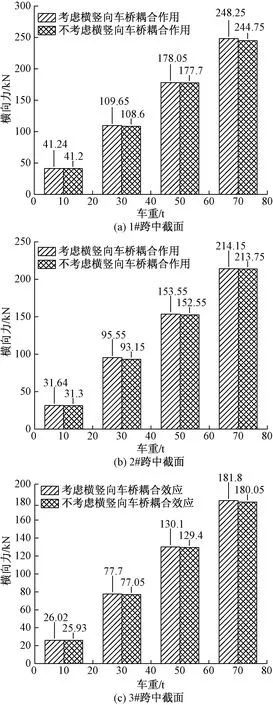
图7 曲线桥跨中横向力对比Fig.7 Comparison of transverse forces in mid-span of curved bridge
由图7可知,随着车重的增加,各跨中截面的最大横向力逐渐变大,这与不考虑车桥耦合作用变化趋势一致。车重相同的情况下,各个跨中截面的横向力比不考虑横竖向车桥耦合作用的数值大。
3.3.2 曲线桥横向位移
提取考虑横竖向车桥耦合作用下曲线桥跨中截面产生的横向位移,其时程曲线如图8所示。
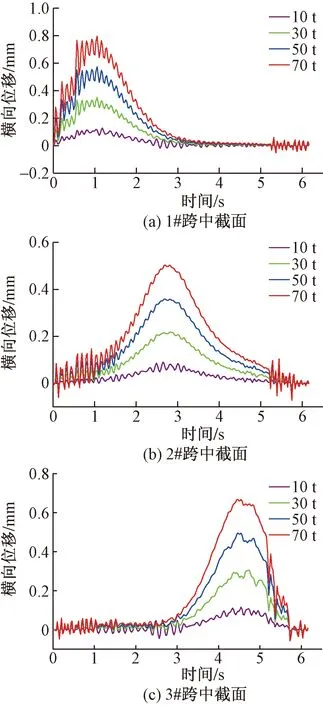
图8 曲线桥跨中横向位移时程曲线Fig.8 Time-history curve of lateral displacement in mid-span of curved bridge
由图8可以得出如下结论:考虑横竖向车桥耦合作用下,各跨中截面的横向位移时程变化曲线具有一定的波动性,特别是车辆刚驶入桥面和离开桥面时波动性比较明显,但是1#、2#、3#跨跨中截面横向位移变化趋势同于不考虑横竖向车桥耦合情况。不同车重汽车上桥,曲线桥跨中截面横向位移变化趋势相同,都逐渐增大,随着车重的增加,曲线形状越陡,这与不考虑车桥耦合作用变化趋势一致。是否考虑车桥耦合作用,横向位移的峰值所出现的时间点会存在一定的差别,但差别不大,在0.2 s之内。为了进一步确定车重对横向位移的影响,提取不同车重下各跨中截面横向位移的最大值。其跨中截面横向位移的最大值如表6所示。
由表6可知,增加车重,各截面的横向最大位移值也逐渐变大,这与不考虑车桥耦合作用产生的结果是一致的,70 t车重作用下,1#跨中截面横向位移最大值能达到0.796 mm,比不考虑横竖向车桥耦合作用增大了10.25%,因此在对曲线桥横向动力响应进行研究时,有必要计入车桥耦合效应。
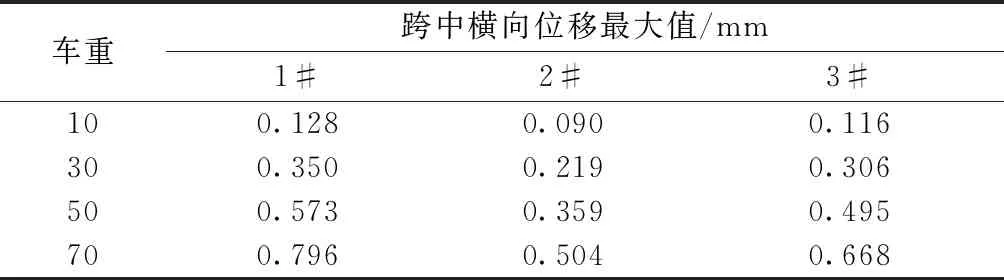
表6 跨中横向位移最大值
综上所述,是否考虑横竖向车桥耦合作用,对曲线桥的横向位移进行对比分析,绘制柱状图,如图9所示。
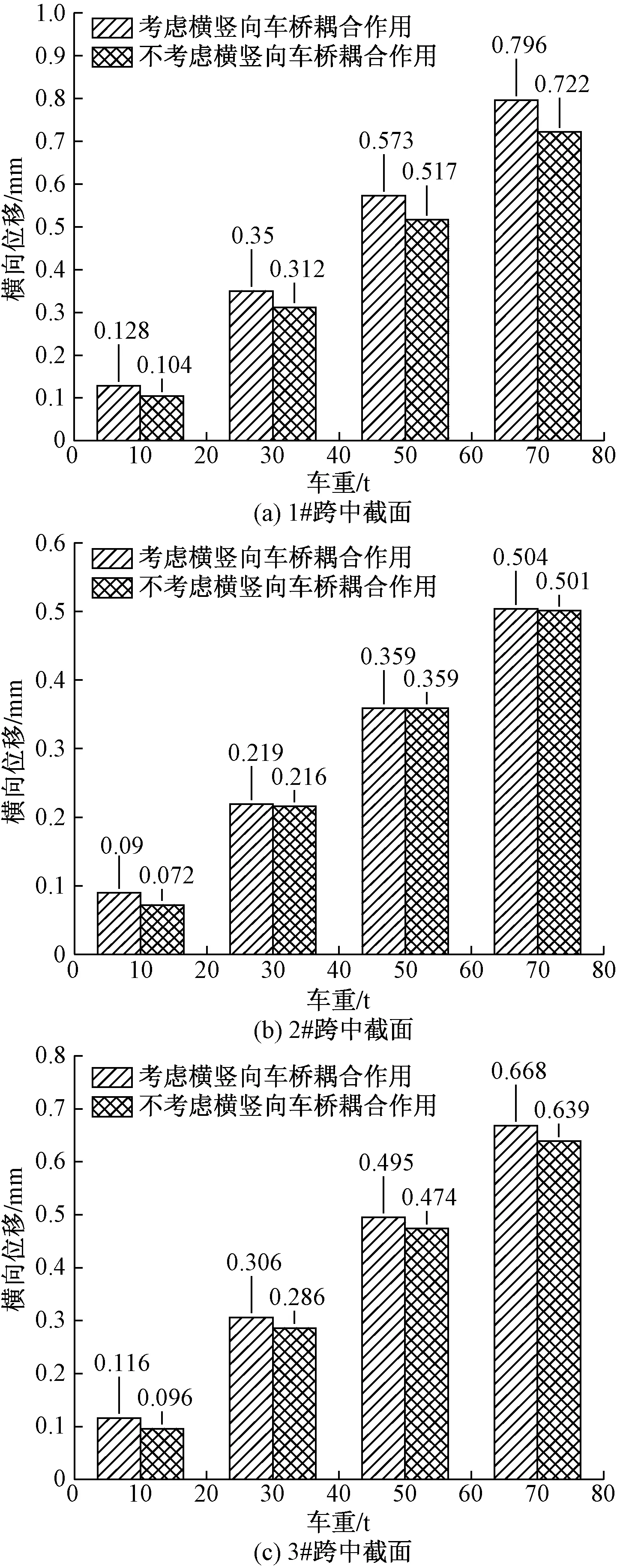
图9 曲线桥跨中横向位移对比Fig.9 Comparison diagram of transverse displacement in mid-span of curved bridge
由图9可知,随着车重的增加,各跨中截面的最大横向位移逐渐变大,这与不考虑车桥耦合作用变化趋势一致。车重相同的情况下,各个跨中截面的横向位移比不考虑横竖向车桥耦合作用的数值大,其中1#跨中、3#跨中横向位移变化最为明显。
4 结论
从车辆自重入手,分析不同车重下考虑横竖向车桥耦合作用曲线桥的动力响应情况,得到以下结论。
(1)曲线桥前两阶振型以竖向振动为主,三阶振型除了竖向振动以外,还会伴随着轻微的侧向的弯扭耦合振动,而高阶振型,弯扭耦合振动效应明显。
(2)不考虑车桥耦合作用,曲线桥横向力、横向位移时程曲线比较圆滑,无波动产生;考虑到横竖向车桥耦合作用,横向力和横向位移的时程曲线会产生波动性,尤其是车辆刚驶入桥面和离开桥面时波动性较为明显
(3)随着车重增加,相同跨跨中截面横向力、横向位移最大值也逐渐增大,这与不考虑车桥耦合作用变化趋势一致。
(4)车重相同的情况下,各个跨中截面的横向力和横向位移均比不考虑横竖向车桥耦合作用的数值大。
