三峡库区滑坡涌浪对趸船撞击力的影响

2020-07-14徐晓菲王平义

科学技术与工程 2020年17期

徐晓菲，王平义

(重庆交通大学河海学院，重庆 400074)

滑坡是一种自然现象，主要是指斜坡上的土体和岩体，在受到了河流冲刷、地下水活动、地震或人为因素影响时，在重力的作用下滑落至水中[1]。通常在水库蓄水之后，受到水库水位及水库运行等众多因素的影响，库区内大量本身地质条件差，存在安全隐患的斜坡均会暴露出来。结果在雨水河流冲刷等外界条件刺激下，导致岸坡沿着软弱面或软弱带向下滑落。当岸坡发生塌滑时，体积巨大的岩体会在短时间内滑至库区内，此时将激起巨大的涌浪。而涌浪从产生至消失的整个过程都将对一定范围内的建筑物、船舶甚至人员等造成伤害。

三峡工程自蓄水后，滑坡事故频发。从三峡大坝前缘到回水末端的河段称为回水区，回水区又分为常年回水区和变动回水区。变动回水区的显著水文特征为水位落差大，综合考虑各方面的限制条件，建港时大多时候采用斜坡式码头。斜坡式码头一般是通过趸船与斜坡道的连接，趸船为无动力、矩形平底装置，供货物装卸运输、旅客或者车辆上下。当岩体激起涌浪时，最先受到影响的即为趸船设备。趸船在涌浪作用下，易发生漂移、侧翻甚至破坏。同时趸船对码头的撞击力，不仅影响趸船本身稳定，还会对码头结构造成伤害。

中外与船舶、趸船相关的研究众多。陈嘉琴[2]首次通过假定船舶-浮码头-撑墩式复合体系，对船舶靠岸的撞击问题进行动力分析，确定撞击力、撑杆内力以及趸船的动倾角等。之后陈嘉琴等[3]又在之前的研究基础上，对复合体系非线性动力方程采用样条加残配点法进行积分，并采用切线刚度及拉格朗日插值函数，求得撞击力、撑杆内力最大值。Sasa等[4]通过数值模拟，对单点锚泊船只在风浪作用下的纵荡、横荡等进行研究，重点分析船舶走锚情况。Isaacson等[5]提出了水动力系数的数值方法，对研究趸船撞击力给出了理论参考。李泳龙[6]以重庆地区码头作业区为依托，采用振动频率法，对斜坡式码头趸船的系泊设备进行了测试和改造，有效避免趸船缆绳断裂事故的发生概率。张婕[7]通过建立三峡库区物理模型，对滑坡涌浪作用下船舶的撞击力与系缆力的影响因素进行了研究。王平义等[8]通过水槽物理模型，确定了船舶撞击力与涌浪初始波高、水体附加系数等相关关系，并提出了船舶对高桩码头撞击力的计算公式。胡杰龙等[9]在物理模型的基础上，利用多元回归分析提出了船舶锚链拉力的经验公式。杨静黎[10]通过运用MIDAS软件，分析得到影响趸船系缆力的主要因素，并对其系缆力敏感性进行了分析。Sha等[11]采用有限元模型和数值模拟的方法，对撞击船和撞击浮筒的结构变形和能量吸收进行了研究，并提出一种可用于初步设计阶段的动态冲剪校核方法。Sha等[12]分别进行了冲击试验和数值模型，评估驳船的冲击力和码头的稳定性，提出了预测冲击峰值力和冲击峰值的经验公式。Mostafa等[13]运用数值模拟，建立一个程序来分析由数个浮码头组成的浮码头的运动，并根据码头承受荷载，对其总体性能进行评估。Sha等[14]在LS-DYNA中建立了船墩碰撞数值模型，推导出基于碰撞条件的冲击力时程预测简化公式。戴磊等[15]利用小波变换的方法，发现涌浪具有频散波特性，经过多元线性回归分析，得到与涌浪相关的经验公式。Sha等[16]基于密集数值模拟结果的经验方程，用来估计桥墩的动力冲击荷载，将桥梁结构简化为非线性单自由度系统，计算其动力响应。Huang等[17]通过试验模拟三峡库区两种常见的高边坡破坏类型，建立了原波最大振幅估计的二维无量纲方程。Panizzo等[18]运用简单的物理实验，将小波变换应用于波浪测量分析中，研究了冲击波的快速性、溢流结构的反射和水槽的截流现象。董涛[19]以长江上游某大水位差架空式斜坡式码头为研究对象，验证了坡道、桩柱结构等在水流作用下的稳定性和安全性。Nam等[20]采用经典有限元方法，直接求解了船舶和系泊驳船在码头附近的势流。并通过改变仿真参数，对船舶通过效应及其波浪对水动力的影响进行了研究。

综合上述研究多是根据理论分析得到影响趸船撞击力因素，或船舶受水流影响对结构物撞击特征进行分析，试验也多用于分析滑坡涌浪本身特性。本文则是采用物理模型试验的方法，推导滑坡涌浪对趸船撞击力的影响，并得到趸船撞击力计算公式。

1 模型试验

1.1 河道设计

1.2 码头结构设计

斜坡式码头是内河较大水位差港口中常用的一种码头形式，依据工程原型实际，试验模型采用架空式斜坡式码头。此类斜坡式码头的特点为透水性佳，对岸坡水流影响较小。为确保试验全面覆盖设计工况，模型采用汛期防洪限制水位145 m为码头坡脚高程，190 m为坡顶高程。斜坡道长度为180 m，斜坡道坡度为1∶4，斜坡道宽度为12.8 m，两道间距为28 m。采用桩柱式墩台，共3跨，每跨之间分别安置3根直径为1.6 m的桩柱连接。依据1∶70几何比尺，得码头设计图如图1所示，并制作码头模型，如图2所示。

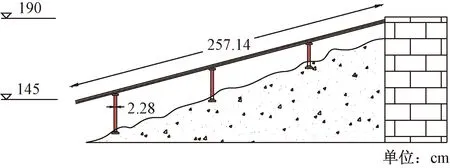
图1 斜坡式码头设计Fig.1 The blueprint of sloping wharf

图2 斜坡式码头模型Fig.2 The model of sloping wharf

码头前沿设置一个2 000 t钢制趸船泊位，趸船外侧为3 000 t船舶泊位。趸船与船舶具体参数统计数据如表1、表2所示。

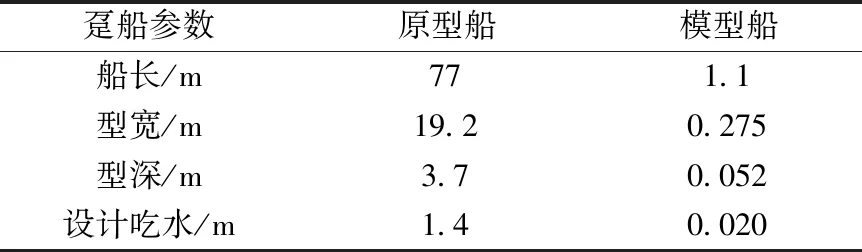
表1 趸船参数统计Table 1 The statistics of pontoon parameters

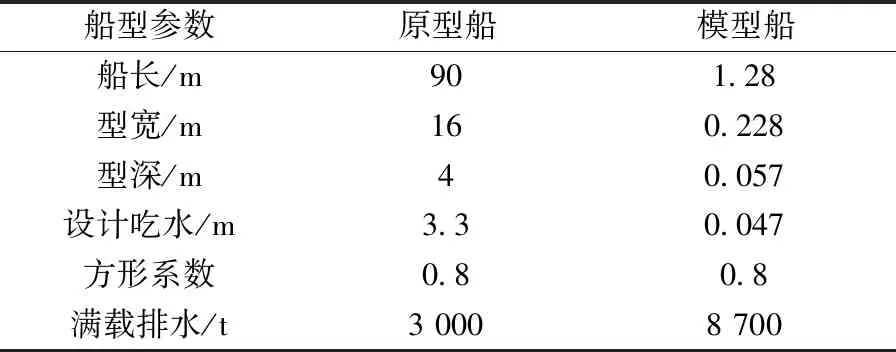
表2 船舶参数统计Table 2 The statistics of ship parameters

为了同时实现模型与原型的外形相似和物理相似，模型利用了浮吊模型进行配重。趸船利用前三后三的抛锚方式来固定，船舶则通过内八字缆的系缆方式与趸船相连接。试验时参考设计规范，在综合考虑趸船锚链强度、其锚链抛出长度和悬链线状态下，采用链径为0.5 mm的不锈钢锚链模拟趸船锚链原型。利用坚韧又有一定松弛度直径为35 mm Kevlar绳模拟缆绳。两种材料均符合外形、强度要求，满足试验中对撞击力与系缆力的测量要求。图3所示即为趸船、船舶模型。

图3 趸船、船舶模型Fig.3 The model of pontoon and ship

1.3 试验工况设计

根据三峡水库实际水位，分别选择汛期防洪限制水位145 m、枯水期消落水位155 m，以及正常蓄水位175 m三级水位，作为低、中、高水位进行试验。结合概化河底平均高程93.55 m，计算得出模型试验三级水位分别为0.74、0.88、1.16 m。

滑坡体位于码头正对岸，通过采用摆置不同方量的滑块，并利用滑架推入水中进行模拟，在参考大量资料的基础上，最后选取4种不同组合方式的滑坡体进行试验，既1×0.5×0.6、1×1×0.4、1×1.5×0.2、1×1.5×0.6 m3。同时为了更好地模拟岩质滑坡体，通过把滑坡体进行散体化模拟岩体块石之间的缝隙。采用相同材质制作5种型号的块体，通过不同的排列组合模拟滑坡体。具体的块体尺寸如表3所示。

表3 滑块模型尺寸Table 3 The size of slider models

在改变滑坡体的体积与河道水深之外，试验根据对库区滑坡区的资料分析，选取了两种典型的滑坡坡度，即40°、60°进行对比。

1.4 试验测量系统

撞击力通过码头前沿安装重庆交通大学自主研制的撞击护舷传感器与拉力片建立电桥，通过转换卡和数据采集软件测量。

2 滑坡涌浪对趸船撞击力的影响

2.1 趸船撞击力的变化规律

如图4所示，即滑坡体方量为1×1.5×0.6 m3、水深为116 cm、入水角度为60°的情况下，滑坡体从入水前至水面逐渐恢复平稳的150 s左右时间内的趸船撞击力历时曲线。通过历时曲线可以观察到撞击力为脉冲值，图4(a)和图4(b)分别为趸船船首、船尾处对斜坡式码头撞击力历时曲线。由于传感器用的拉力片为悬臂梁结构，且具有一定弹性，受力后的恢复过程，撞击力历时曲线会出现负值。趸船为矩形船底，船首船尾传感器对称安装，滑坡体在正对岸滑落。由于趸船撞击力不仅受波浪的影响，同时锚链的松弛度、系缆船舶的撞击力等，都是影响趸船撞击的重要因素。故船首船尾的撞击力历时曲线变化大致相似，但也存在一些差别。根据图4可看出，滑坡体入水后第1个脉冲值并不是最大的，统计发现往往第2、3个脉冲值处为最大撞击力点。无论船首还是船尾，最大撞击力出现在第2或者第3个脉冲值的概率达75%。这说明最初涌浪造成的撞击力并不是最严重的，反而是前期反复叠加的波浪对趸船撞击力的影响更大。据观察最大撞击力后第1、2个脉冲值仍较大，基本与最大撞击力前的脉冲值呈对称状。通常第5个或者第6个脉冲值开始，撞击力会骤减，符合指数衰减规律，之后则维持周期性的缓慢衰减变化，符合明槽水流的沿程水头损失规律。

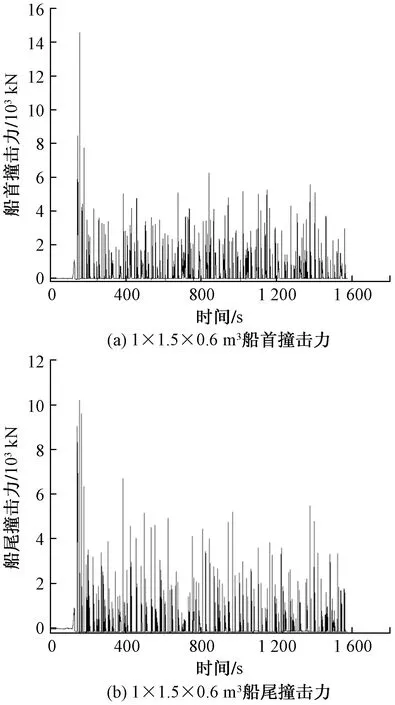
图4 趸船撞击力历时曲线Fig.4 The time-domain figure of the impact force of pontoon

故趸船撞击力历时曲线可总结为，起初短时间内骤增至最大值，之后与最大值前变化呈现对称状，最后骤减进入一个周期性缓慢衰减过程。

2.2 趸船撞击力的影响因素

根据之前滑坡涌浪对直立式码头作用的研究资料，发现滑坡体、涌浪的一些特性对力会产生不同的影响，包括滑坡体的方量、河道水深、滑坡体倾角以及初始波高等，均对力的研究有重要的意义。

2.2.1 滑坡体方量对趸船撞击力影响

滑坡体方量为影响撞击力的重要因素，在对比了多组试验后发现，方量与趸船撞击力呈正比。在3种不同水深情况下，虽其增长趋势不同，但均为方量越大趸船撞击力越大。

图5 不同水位同方量对比Fig.5 The comparison of the same square amount at different water levels

在实际情况下，相似方量的滑坡体形态也可能千差万别。对比图5两组趸船撞击力的历时曲线，两组的方量大小相同，入水角度均为60°。第1组为1×0.5×0.6 m3，横切面类似于正方形。第2组为1×1.5×0.2 m3，横切面类似于横放长方形。从图5观察到，虽然随着水位的变化两组试验大小比会有轻微的波动，但总体方量一样，其撞击力大小差异不大。

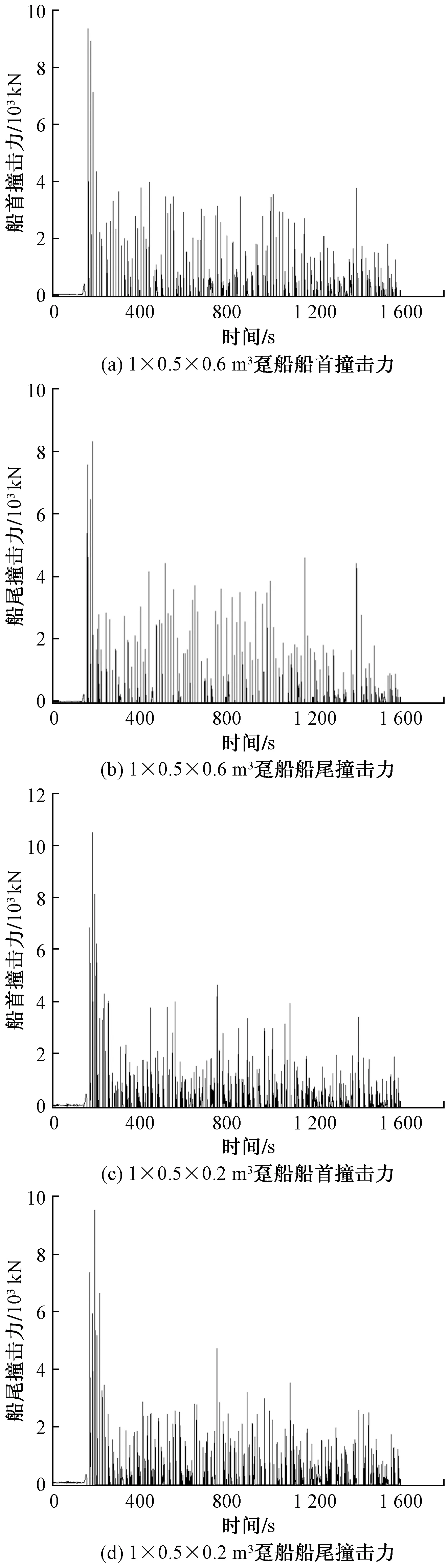
图6 同方量滑坡体趸船撞击力历时曲线Fig.6 The time-domain figure of the impact force of pontoon with the same volume of landslide

图6所示为方量相同，但宽高组合不同的两个工况的撞击力历时曲线。据图6观察，两组最大撞击力相差不大，但历时曲线存在明显差异。经统计1×0.5×0.6 m3组合的试验组，第2个脉冲值为最大撞击力的概率为50%，第3个脉冲值为最大撞击力的概率仅为16.7%。而1×1.5×0.2 m3组合的试验组，第2个脉冲值为最大撞击力的概率为33.3%，3个脉冲值为最大撞击力的概率高达66.7%。可得结论，虽同方量的滑坡体最大撞击力基本相同，但不同的形态却会影响最大撞击力发生的时间。

2.2.2 水深对撞击力的影响

三峡水库自建成以来，最明显的水文条件特征为水位落差大。不同水位时期，若山体发生滑塌，其产生的涌浪特性以及对结构物的影响等都将有所差异。故分析不同水位对趸船撞击力的影响存在一定的研究意义。

为了更加直观地观察水深对趸船撞击力的影响，把3种水位多个工况的撞击力最大值进行对比。图7所示为方量、宽度高度组合方式、滑坡体角度等多种因素保持相同的情况下，不同水位的对比。由图7可清晰地观察到，大多工况情况下，中水位(0.88 m)时趸船撞击力相比低水位(0.74 m)、高水位(1.16 m)都较大。而低水位(0.74 m)的趸船撞击力也要大于高水位(1.16 m)。此现象说明一定范围内，趸船撞击力会随着水位增加而变大，但到达一个峰值之后，由于水流阻力也会随水位的增加而变大，反而对趸船撞击力产生了削减作用。

图7 不同水位撞击力Fig.7 The impact forces at different water levels

2.2.3 波周期、初始波高对趸船撞击力的影响

图8所示为趸船撞击力分别随初始波高与周期的变化规律。可见，初始波高为6～9 m，撞击力随初始波高的增加为一个急剧下降的趋势。9～11 m为一个先缓慢变化，之后又急剧上升的过程。11 m后撞击力随初始波高的波动呈现较规律的波动。再观察趸船撞击力随周期的变化过程，曲线整体呈上升趋势。14～16 s期间为振动变化过程，在急剧上升之后是急剧下降，之后缓慢上升紧接着又为急剧下降。16～20 s期间为整体上升趋势，17～19 s上升稍缓慢，但整体上升速度较快。20～22 s为下降过程，但22 s后紧接着还是上升趋势。对比初始波高和周期对力的影响，两者规律线均呈现较大的波动。这说明虽然随波能增加，趸船收到的能量也会增大，但是撞击的过程复杂，包括水深、锚链拉力、船舶的撞击、趸船自身船体扭转等因素的影响会造成消能，故趸船撞击力随初始波高、周期的变化是一个波动的过程。

图8 趸船撞击力随初始波高、周期变化Fig.8 Changes of impact force of pontoon with initial wave heights and period

3 船舶撞击力对趸船撞击力的影响

大多数斜坡式码头均设有趸船，其作用不仅是码头前方的作业场所，还要具备适应水位变化、机动灵活和便于调动转移的特点。在斜坡式码头的结构中占有重要的地位。但是近几年的趸船事故却频频发生，若发生滑坡事故，趸船易因船舶对其的撞击发生侧翻而造成人员财产伤害。故研究船舶对趸船的撞击力规律存在一定的必要性。

3.1 船舶撞击力与趸船撞击力的相关性

图9所示为不同水位、不同方量的多组试验方案，把所有试验组中船舶撞击力最大值出现的时间与趸船撞击力最大值出现的时间进行比较。

图9中横坐标为撞击力最大值出现时间，纵坐标为最大值撞击力值。故可知同组试验中船舶和趸船撞击力最大值出现的时间基本同步。

图9 船舶、趸船最大撞击力出现时间Fig.9 The maximum impact force of ship and pontoon

表4所示为多组试验方案中船舶撞击力与趸船撞击力最大值差值，可见最大的差值甚至能够比船舶本身撞击力的值更大。故知趸船对码头撞击力不仅来自于波浪的推动力，船舶对于其撞击力也是使其撞击力加大的一个重要因素。趸船撞击力来源于自身的重量与船舶的重量，两船合并同时撞击码头。

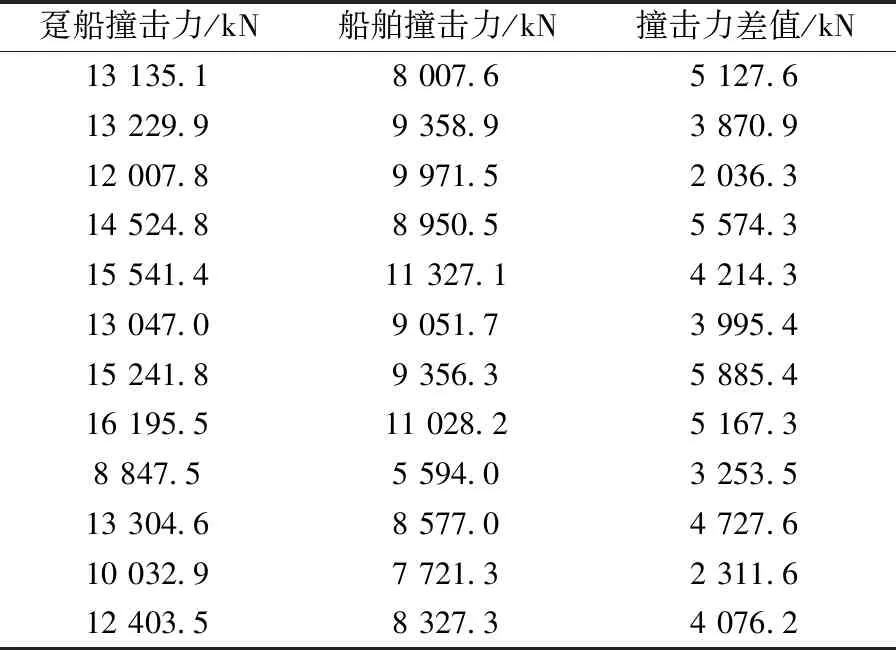
表4 各工况船舶、趸船撞击力差值对比Table 4 Comparison of impact force in different working conditions between ship and pontoon

3.2 船舶对趸船撞击力回归分析

船舶的撞击力计算分为两类，一类为靠岸撞击力，一类为横浪作用下的撞击力。船舶对趸船的撞击力即为横浪作用下的撞击，此类撞击的影响因素较多，计算复杂。经过对之前资料的总结和本次试验的归纳，船舶的撞击力受初始波高H、水位h、涌浪周期T等条件的影响。分别采用多元线性函数、多元指数函数、多元幂函数进行回归分析，得以下3个公式：

F/(ρh4/T2)=-0.000 000 268 8-0.000 026 472×(H/h)+0.000 000 354 1(T2g/h)

(1)

F/(ρh4/T2)=0.000 003 263 2e[-10.664 39(H/h)+0.052 72(T2g/h)]

(2)

F/(ρh4/T2)=0.000 000 032 6(H/h)-0.294 68(T2g/h)1.396 44

(3)

式中：F为船舶撞击力计算值，kN；ρ为水密度，为1 000 kg/m3；h为水深，m；H为初始波高，m；T为波周期，s。分别把试验数据与上面3个公式所得的计算数据进行对比，结果发现，式(2)多元指数函数的拟合度最好，R2=0.91。图10所示为船舶多元指数函数拟合图。