基于车桥耦合振动的钢管混凝土系杆拱桥动力响应分析



基于车桥耦合振动的钢管混凝土系杆拱桥动力响应分析

张耀1,2，孙增寿2

(1.同济大学 土木工程学院，上海 200092；

2.郑州大学 土木工程学院，河南 郑州 450001)

摘要：为研究钢管混凝土系杆拱桥在车辆荷载作用下的动力效应，利用ansys二次开发功能编写基于车桥耦合理论的车桥耦合振动分析程序，分析车速、车重以及路面不平顺等级3个因素对拱肋、端部吊杆及桥面跨中等关键部位动力响应的影响。分析结果表明：随车速、车重及桥面不平顺等级降低，桥梁跨中节点位移响应峰值不断增大，拱脚、1/4拱肋及拱顶截面处的应力最大值不断增大，最小值不断减小；但拱顶截面应力响应峰值对车重、车速及桥面不平顺等级的敏感程度较拱脚与1/4拱肋截面处的低。此外，桥梁跨中加速度响应峰值及端部吊杆应力幅对车重20 t最敏感，端部吊杆的应力幅随车速提高反而降低，当桥面不平顺等级为D级时端部吊杆应力幅达到186 MPa。最后，对比车-桥振动响应分析发现，随着桥面不平顺等级降低、行车速度提高，将会引起车体较大的竖向加速度峰值，进而引起桥梁结构较大的竖向位移。

关键词：钢管混凝土系杆拱桥；车桥耦合；车速；车重；桥面不平顺等级

在桥梁运营过程中，一方面车辆的振动响应激励着桥梁振动，另一方面桥梁的振动效应又影响着车辆的振动；通常桥梁结构在行车荷载作用下的动力响应往往要大于等值的静力响应。早期关于车桥耦合振动分析的研究主要集中于梁桥[1-2]，特别是简支梁桥；随着车辆过桥引起的振动影响引起国内外学者的重视，一些大跨度桥梁的研究，如斜拉桥[3]、悬索桥[4]，也取得了一定的成果。相对于其他桥型，关于大跨度钢管混凝土系杆拱桥的研究还不够充分。许士杰等[5]为模拟车辆通过钢管混凝土拱桥引起的动态响应，提出将车辆与桥梁看作一个相互作用的整体系统的方法，并通过数值算例验证了方法的实用性与通用性。杨建喜等[6]将单一车辆模型简化为匀速移动的集中荷载组，讨论了不同车速下钢管混凝土系杆拱桥短吊杆的动力特性，结果表明短吊杆的轴力放大系数与车速成正比，且短吊杆应力峰值出现在车辆过桥后的自由振动阶段。然而，上述研究只选用单一车辆，甚至不考虑车体质量的惯性力的影响，不能模拟真实过桥车辆所引起在役拱桥的动力响应，而这却是桥梁维修管理部门关注的重点。据此，本文基于车桥耦合理论，分析在随机多车辆作用下，不同车速、不同车辆载重及不同路面不平顺等级对安阳文峰桥关键部位动力响应的影响。为桥梁维修管理部门的限速、限载及维修决策提供理论依据。

1车桥耦合振动微分方程的建立与求解

有限单元法是目前研究车桥耦合应用最为广泛的方法，特别是在已有的通用有限元程序(如ansys, abaqus等)基础上进行二次开发；通常分别建立车辆和桥梁的有限元模型，通过考虑两者在接触点的相互作用来建立动力学方程；并采用数值解法求解。

1.1空间车辆模型

以车桥系统的静力平衡位置作为参考建立如图1所示的坐标系，车辆模型共考虑9个自由度，包括6个车轮的竖向平动，车体的俯仰、转动及竖向平动[7-9]。图中，Mi为车辆对应部位质量，Zi为车辆对应位置的竖向位移，θv为车体俯仰角，φv为车体侧倾角，Kui和Cui分别为车轮处的车悬架刚度和阻尼，Kdi和Cdi分别为6个车轮的轮胎刚度和阻尼(车辆各参数值如表1所示)。

1.2钢管混凝土系杆拱桥空间模型

安阳文峰立交桥主桥是一座钢管混凝土系杆刚架拱桥，建于1991年，跨度138 m，桥面宽31 m，两片拱肋中心距为16 m，机动车道为双向四车道，设计车速40 km/h，设计荷载汽-20、挂-100，横跨京广铁路正线及编组站。其中钢管内混凝土为C40，桥面板、横梁、纵梁混凝土C35。在桥梁有限元建模中，钢管混凝土采用双单元模型，即在同一段有限元模型中将钢管和混凝土分别作为2根具有不同物理特性的杆件，但要保证两者共节点。拱肋、横撑、桥面系纵梁与横梁以及桥墩采用beam189单元进行模拟，系杆与吊杆采用只受拉的杆单元Link10来模拟，桥面板采用壳单元shell63来模拟。钢管混凝土系杆拱桥空间有限元模型建立如图2所示，拱桥有限元模型中的材料特性如表2所示。

为了验证模型的准确性，对钢管混凝土系杆拱桥进行模态分析，提取主要的前3阶竖向模态，并与实测值进行比较(如表3所示)。从表3中可以看出有限元模型较实际桥梁的竖向刚度稍大，但具有一定的精度，能够满足工程要求。

表1　车辆参数

表2　拱桥材料特性

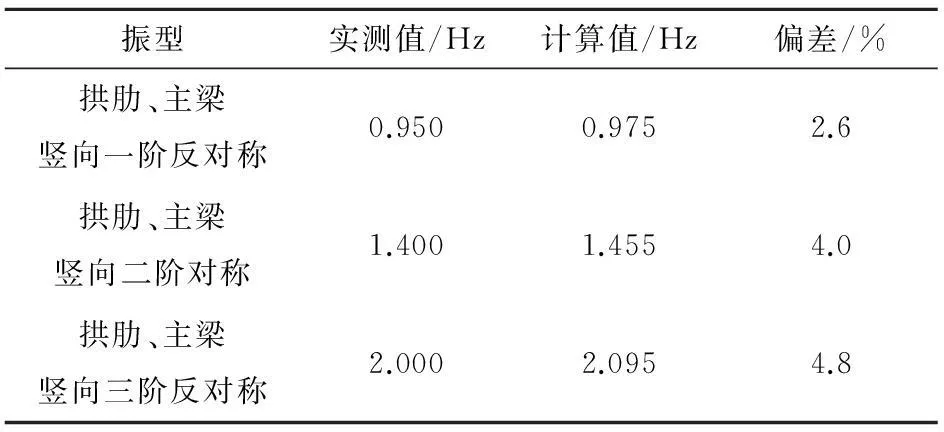
表3　拱桥实测与计算频率值

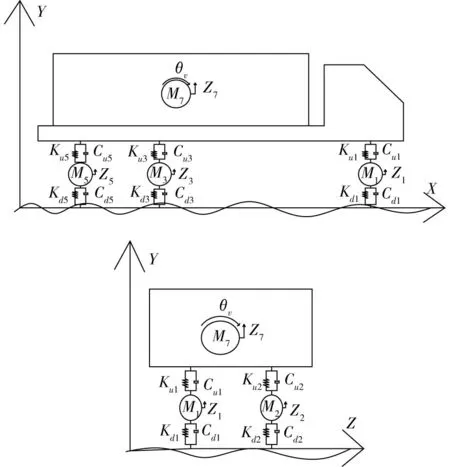
图1　车辆模型示意图Fig.1 Schematic diagram of vehicle model

图2　桥梁结构有限元模型Fig.2 Bridge finite element model

1.3车桥耦合振动微分方程建立与求解

基本假定：1)车轮与桥梁始终保持接触状态；2)过桥车辆保持匀速行驶，忽略车辆对桥梁的纵向及横向作用。

在车桥耦合系统中，车辆和桥梁2个子系统通过车轮与桥梁之间的位移协调条件和受力平衡2个条件形成一个整系统。车辆与桥面之间的位移协调条件指车辆在桥上行驶过程中，车轮始终与桥面保持紧贴，不发生脱离，即行驶中车辆的竖向位移受到桥梁竖向位移的限制与约束。同时，将桥面不平顺值与桥梁位移叠加组合而成的等效不平顺值作为激励，输入到车辆子系统中。受力平衡是指在车辆与桥面接触点上，车桥之间形成一对大小相等方向相反的作用力与反作用力平衡力系。因此，车-桥是通过接触点的位移协调与竖向力的平衡条件来实现耦合作用。运动方程可以写为：

(1)

式中：[Mv]和[Mb]为车辆与桥梁的质量矩阵；[Cv]和[Cb]为车辆与桥梁的阻尼矩阵；[Kv]和[Kb]为车辆与桥梁的刚度矩阵；{Fbv}和{Fvb}分别为车辆对桥梁和桥梁对车辆的作用力。

第i个车轮与桥梁之间的作用力与反作用力可写为：

(2)

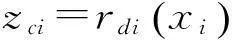
车桥耦合系统是时变系统，通常在计算时以第i时间为参考坐标和初始条件计算第i+1时间步的瞬态响应。当车轮位置在板单元内部时，一般利用静力平衡计算单元等效节点力(忽略弯矩传递)，如图3(a)所示；本文为简化计算，在有限元建模时，以行车线作为板单元的边界，且板单元沿桥纵向的长度是沿桥横向的一半(如图3(b))。因此，可采用图3(c)简化计算:

(3)

(4)

式中:ui和uj分别是节点i和j的位移；vi和vj分别是节点i和j的速度。

采用Newmark-β法求解动力方程组，积分步长为1/4v(v为行车速度)，其迭代收敛准则选用位移收敛准则：

(5)

式中:Zi+1和Zi分别为第i+1次和i次迭代步车-桥之间接触点的位移值。

图3　节点等效荷载计算简图Fig.3 Diagram of equivalent joint load

1.4桥面不平顺数值模拟

桥面不平顺等级是根据路面功率谱密度对路面粗糙程度的划分。如果桥面不平顺是平稳的、具有各态历经性的高斯随机过程，可以利用谐波叠加法来模拟桥面的不平顺。国家标准《车辆振动输入—路面不平度表示方法》(GB7031)将路面不平度划分为A-H共8个等级，但考虑到文峰桥的路面的实际情况，本文只模拟A，B，C和D共4个等级来研究路面不平度对桥梁动力效应的影响[13],如图4所示。根据标准谐波叠加公式为：

(6)

图4　桥面不平顺样本函数Fig.4 Sample function of roughness

式中：αk2=4Gd(nk)Δn；Gd(nk)为路面功率谱密度；空间频率nk=nl+(k-1/2)Δn,k=1,2，…，N；Δn=(nh-nl)/N；nh和nl为所研究空间频率的上、下限；圆频率ωk=2πnk。

(7)

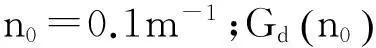
1.5车距模拟

根据公路桥梁车辆荷载研究课题组对我国车辆情况的调查统计分析，车辆间距具有随机特性，服从均值为4.828，方差为1.116的对数正态分布[10-11]，即：

(8)

式中：y=lnx，x为车辆间距；μy为均值，σy为方差。利用matlab调用对数正态分布函数生成随机车距样本。

2钢管混凝土系杆拱桥动力响应分析

车辆按双向4车道布置，如图5所示；每车道布置1列车队，每列车队中车距服从1.5节所述随机分布，且前后车辆在纵向沿同一车道在同一直线上；每辆车在横向位于车道的中部(距车道线0.75 m)。行驶中，车流不间断，忽略车辆的横向偏移，并假定每列车队的第1辆车同时上桥。

图5　车道布置示意图Fig.5 Deck layout

为研究车速、车体质量与路面不平顺程度对钢管混凝土系杆拱桥的振动响应影响，分析在随机车距下一个行车周期(跨度/车速)所引起的桥梁动力效应，并分别考虑以下3种工况。

1)在研究车体载重对拱桥振动效应的影响时，分别考虑10，15，20和30 t车重，车速为72 km/h，路面不平顺等级为B级；

2)在研究车速对拱桥振动效应的影响时，分别考虑车速36，48和72 km/h，车体质量为20 t，路面不平顺等级为B级；

3)在研究路面不平顺对拱桥振动效应的影响时，分别考虑不平顺等级：A级，B级，C级和D级，车速为72 km/h，车重为20 t。3种工况中的车距同属于一个随机样本。

2.1跨中节点动力响应影响分析

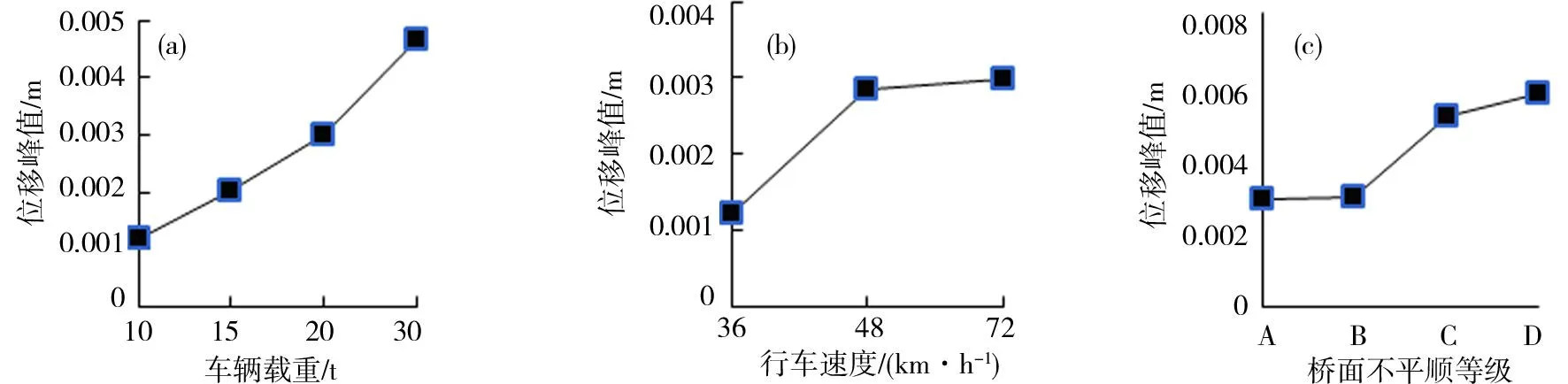
(a)工况1；(b)工况2；(c)工况3图6　不同工况下跨中节点位移峰值变化曲线Fig.6 Curve of maximum dynamic displacement at mid-span point under different conditions

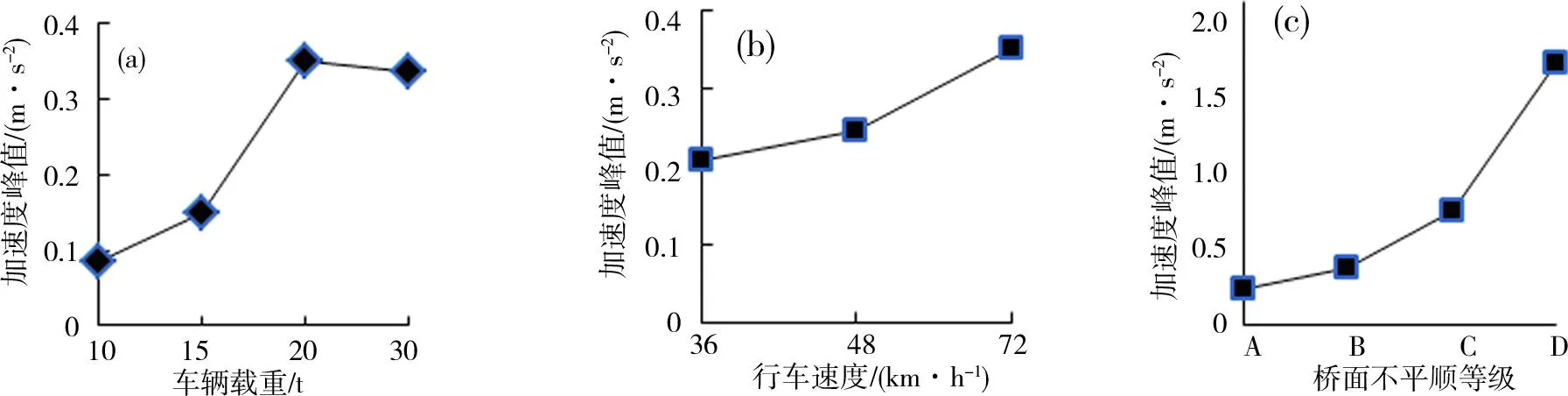
(a)工况1；(b)工况2；(c)工况3图7　不同工况下跨中节点加速度峰值变化曲线Fig.7 Curve of maximum acceleration at mid-span point under different conditions

图6~7分别为桥梁跨中的位移响应和加速度响应峰值随车重、车速与桥面不平顺等级变化的曲线。由图可知，随车速、车重及桥面不平顺等级提高，跨中位移响应峰值不断增大；车重为30 t时跨中位移峰值为0.004 7 m，几乎是车重为10 t的5倍(工况1)；相对于车速48 km/h，车速72 km/h的位移响应峰值增大近2倍(工况2)；当桥面不平顺等级为D级时桥梁跨中位移响应峰值为0.007 m，约是A级的3倍(工况3)。加速度响应峰值随车速、桥面不平顺等级变化有相似规律，值得注意的是：加速度响应峰值对车重变化存在最敏感值，当车重为20 t(工况3)时，加速度响应峰值达到最大值0.35 m/s2，车重30 t加速度峰值反而降低。由此可见，车重和桥面不平顺是引起桥梁产生过大位移振动的主要因素，且桥面不平顺是桥梁结构产生惯性力的主要因素。由此可见，桥面不平顺是桥梁结构产生惯性力(加速度)相对主要的因素。

2.2拱肋动力效应影响分析

表4~6列出了不同车速、车重及路面不平顺等级下拱肋关键截面的应力(轴同应力+弯曲应力)的峰值。随着行车速度的增加、车重增大、桥面不平顺等级提高，拱脚、1/4拱肋及拱顶截面处的应力最大值随之增大，最小值随之减小，但拱顶截面应力响应峰值对车重、车速及桥面不平顺等级的敏感程度较拱脚与1/4拱肋截面处的低，如在工况一中，相对于车重10 t，车重为30 t时关键截面应力峰值的变化：拱顶(1.5 MPa，-0.8 MPa),1/4拱肋(3.7 MPa,-1.9 MPa)，拱脚(2.5 MPa,-1.8 MPa)。(注：括号内前者为最大应力变化值，后者为最小应力变化值)。

表4　工况1拱肋关键截面的应力响应峰值

表5　工况2拱肋关键截面的应力响应峰值

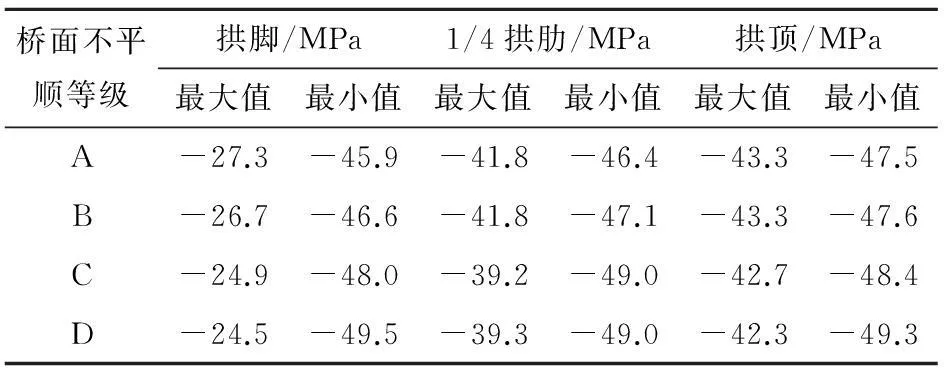
表6　工况3拱肋关键截面的应力响应峰值

(a)工况1;(b)工况2;(c)工况3图8　不同工况下端吊杆应力幅变化曲线Fig.8 Curve of maximum of the stress amplitude in the suspender under different conditions

2.3端吊杆动力效应分析

在车辆荷载作用下，短吊杆的受力较为复杂，且易发生疲劳破坏[6]。因此，下面重点研究端部吊杆在不同车速、车重及不同桥面不平顺等级下的应力幅动力效应，计算结果如图8所示。从图8可以看出，端部吊杆应力幅在车重20 t时达到最大值68 MPa，在车重增大到30 t时反而降低，说明端部吊杆应力幅对车重的最敏感值为20 t。工况2中端吊杆应力幅随车速增大而降低，这是因为应力幅与桥梁振动的程度有关，车重增大会增大吊杆的应力值，并不会导致桥梁结构振动加剧，而车速只有达到使车-桥共振的速度时才会引起较大的应力幅。工况3中端吊杆应力幅随桥面不平顺等级增大而增大，当路面不平顺等级为D 时应力幅达到186 MPa，远大于其他因素变化引起的值。因此，可以认为路面不平顺是引起端吊杆疲劳破坏的主要因素。

2.4车体竖向振动响应分析

车体的竖向振动加速度响应关系到车桥之间相互作用力的大小。影响车体竖向振动加速度响应的因素有桥梁与车辆参数、桥面不平顺等级及行车速度等[14]。这里主要讨论车体质量、行车速度及桥面不平顺等级对车体竖向振动加速度响应的影响。图9为车辆加速度响应峰值在不同车道上的分布(行车速度20 m/s，车重20 t，桥面不平顺等级B)。

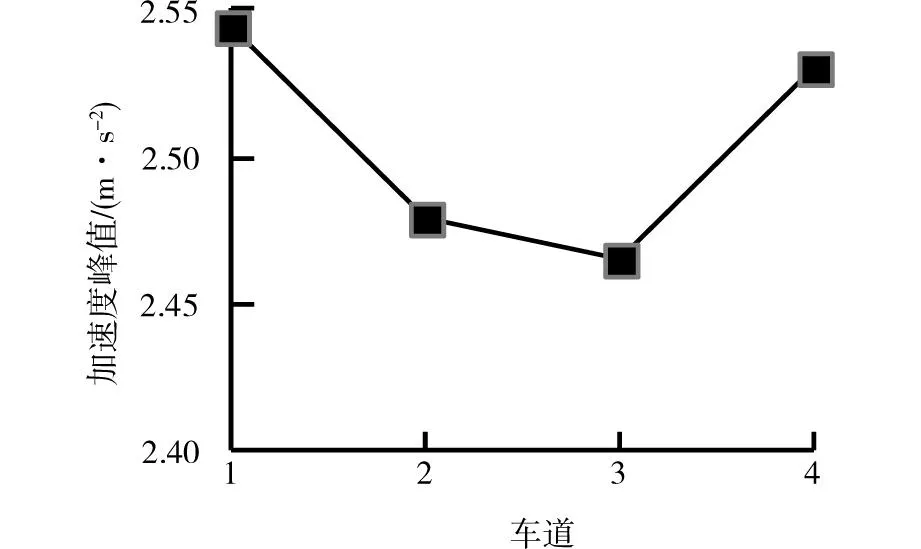
图9　车辆加速度峰值在车道上的分布Fig.9 Distribution of vehicle acceleration peak in lanes

图9显示1和4车道上行驶车辆的车体竖向振动加速度响应峰值略大于2和3车道。因此，本文选取1车道上行驶的具有一个行车周期的车辆进行分析是合理的。图10为车辆的车体竖向加速度响应峰值随车辆载重、行车速度及桥面不平顺等级变化的曲线。图10显示，随着桥面不平顺等级恶化、行车速度增加车体竖向加速度响应峰值不断增强。其中，D级桥面下的加速度响应峰值约是A级的5倍；行车速度为20 m/s时的加速度峰值是行车速度为10 m/s的1.1倍。此外，随着车重的增加，车体的加速度响应峰值逐渐降低。对比桥梁结构跨中位移振动响应，车体竖向加速度峰值响应随车重的增加减小，而桥梁结构跨中位移峰值随着车重增加增大。这是因为桥梁结构受车辆的作用力主要包括车辆重力和惯性力；尽管车体的加速度具有放大车体重力的作用，但在车体加速度小于重力时，车辆重力起主导作用。因此，尽管随着车重增加，车体加速度减小，但车辆对桥梁的作用力并未减小。在相同车重下，行车速度增加，桥面恶化会引起车体竖向加速度响应增加，进而增大车对桥梁的作用力，使得桥梁结构的跨中位移响应峰值增大。

综上可知，适当的限速、限载可以减轻桥梁结构的动力响应，有利于桥梁结构的安全。在桥梁日常维护中，应及时修补桥面，防止因桥面恶化引起结构较大的动力效应而导致桥梁发生损伤。

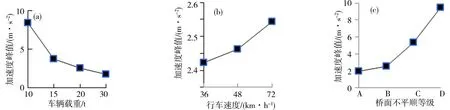
(a)工况1；(b)工况2；(c)工况3图10　不同工况下车体竖向加速度峰值变化曲线Fig.10 Curve of vehicle acceleration peak under different conditions

3结论

1)随着车重、车速及桥面不平顺等级的提高，桥梁跨中位移响应峰值随之增大，桥梁跨中加速度响应峰值对车重的最敏感值为20 t，且随着车速与桥面不平顺等级的提高而增大。

2)拱顶应力峰值对车速、车重及桥面不平顺等因素较拱脚、1/4拱肋应力峰值不敏感；拱脚应力响应峰值对桥面不平顺等级的变化最为敏感。

3)端吊杆应力幅随车速增高而降低，随桥面不平顺等级提高而增大，且变化较大，对车重的最敏感值也为20 t。

4)随着桥面不平顺等级降低，车体加速响应显著增大，进而增大车桥之间的相互作用力，对行车及桥梁安全均不利。在桥梁日常维护中，应及时修补桥面，防止因桥面恶化引起结构较大的动力效应而导致桥梁发生损伤。虽然车重增加会导致车体加速度响应降低，但车对桥梁的作用力会由于车重的增加而增加，因而，桥梁跨中位移响应峰值随车重增加而变大。此外，行车速度的增加会增大车体振动，但幅度不大。

参考文献：

[1] YANG Yeongbin, Lin Binghoung. Vehicles-bridge interaction by dynamic condensation method [J]. Journal of Structural Engineering,1995,123(9):1636-1642.

[2] 李小珍，张黎明，张洁.公路桥梁与车辆耦合振动研究现状与发展趋势[J].工程力学，2008,26(03):230-240.

LI Xiaozhen, ZHANG Liming, ZHANG Jie.State-of-the-art-reviewandtrendofstudiesoncoupling vibration vehicle and highway bridge system [J]. Engineering Mechanics, 2005, 22(1): 218-222.

[3] Guo W H, Xu Y L. Fully computerized approach to study cable-stayed bridge-vehicle interaction[J]. Sound Vib, 2001,248(4):745-761.

[4] XIA H, XU Y L, CHAN T H T. Dynamic interaction of long suspension bridges with running trains [J]. Journal of Sound and Vibration， 2000, 237(2):263-280.

[5] 许士杰，王元丰. 钢管混凝土拱桥与车辆动力相互作用的研究[J].哈尔滨建筑大学学报,1999,32(3):50-54.

XU Shijie, WANG Yuanfeng. Study on dynamic interaction of concrete filled steel tubular arch-bridge with vehicles[J]. Journal of Harbin University of C. E. & Architure,1999，32(3):50-54.

[6] 杨建喜，陈惟珍，古锐. 拱桥吊杆动力特性分析[J]. 桥梁建设，2014,44(3)：13-18.

YANG Jianxi, CHEN Weizhen,Gu Rui. Analysis of dynamic characteristics of short hanger of arch bridge[J]. Bridge Construction,2014,44(3): 13-18.

[7] 王贵春，李武生. 斜拉桥在多车辆作用下的动力响应分析[J]. 桥梁建设，2014,44(6):81-87.

WANG Guichun, LI Wusheng. Analysis of dynamic responses of cable-stayed bridge under action of multiple vehicles [J]. Bridge Construction, 2014,44(6): 81-87.

[8] 夏禾，张楠. 车辆与结构动力相互作用[M]. 北京：科学出版社，2005.

XIA He, ZHANG Nan. Dynamic interaction of vehicles and structures[M]. Beijing: Science Press,2005.

[9] Guo W H. Dynamic analysis of coupled road vehicle and long span cable-stayed bridge system under cross winds [ D]. Hongkong: Hongkong Polytechnic University, 2003.

[10] 王达，刘扬，黄平明. 随机车流作用下双曲线拱桥车-桥耦合振动研究[J]. 中国公路学报，2009,22(06):67-73.

WANG Da, LIU Yang, HUANG Pingming. Research on vehicle-bridge coupled vibration for two-way curved arch bridge under random traffic flow[J].China Journal of Highway and Transpot, 2009,22(06):67-73.

[11] 李武生. 大跨度公路斜拉桥车-桥耦合振动系统安全性与车辆舒适性分析[D].郑州:郑州大学,2013.

LI Wusheng. Analysis on safety and vehicle comfort of vehicle-bridge coupled vibration system of long span highway cable-stayed bridge[D].Zhengzhou:Zhengzhou University,2013.

[12] 刘夏平，孙卓，杨红，等. 运营车辆荷载作用下大跨PC梁桥动挠度特性研究[J]. 公路，2013(7):62-67.

LIU Xiaping, SUN Zhuo, YANG Hong, et al. A study on dynamic deflection characteristics of large span PC girder bridge under vehicle load [J]. Highway, 2013(7):62-67.

[13] 陈宝春，韦建刚，吴庆雄.钢管混凝土拱桥技术规程与设计应用[M]. 北京：人民交通出版社，20011.

CHEN Baochun, WEI Jiangang, WU Qingxiong. Technical specification for concrete filled steel tubular arch bridge and design application[M]. Beijing: People's Commumication Press, 2011.

[14] 陈淮,章长玖,王贵春. 公路简支梁桥车辆走行性及乘坐舒适性研究[J]. 中外公路,2015(2):102-106.

CHEN Huai, ZHANG Changjiu, WANG Guichun. Research on the vehicle runabililty and riding comfort about highway simple supported beam bridge[J]. Journal of China & Foreign Highway, 2015(2):102-106.

(编辑阳丽霞)

Analysis of concrete-filled steel tubular tied-arch bridge under travelling vehiclesZHANG Yao1, 2, SUN Zengshou2

(1. School of Civil Engineering,Tongji University, Shanghai 200092, China;

2. School of Civil Engineering,Zhengzhou University,Zhengzhou 450001, China)

Abstract:A theoretical research work in relation to the dynamic impact to concrete-filled steel tubular tied-arch bridge under modern travelling vehicles was described. The program for bridge-vehicle coupled vibration is compiled by utilizing the secondary development in finite element analysis software ANSYS. The dynamic response of arch rib, suspender and mid-span are discussed respectively in consideration of different vehicle speed, weight and roughness. The results indicate: with the decrease of vehicle speed, weight, and the deterioration of bridge roughness, the dynamic displacement peak of mid-span and the maximum stress of arch foot, 1/4 arch rib and top section increase obviously, while the minimum stress decrease. The maximum stress of top section is relatively less sensitive to the three factors than other sections. Furthermore, the mid-span acceleration response peak and the end suspender stress amplitude are most sensitive to vehicle 20 t. While the end suspender stress amplitude decrease with the increase of vehicle speed. What’s more, there is a most sensitive weight to the suspender stress amplitude. And the end suspender stress amplitude is 186 MPa (fatigue strength 200 MPa) when the bridge roughness degrades to D. Eventually，it can be found that the deterioration of bridge roughness will cause the larger magnitude of vehicle acceleration peak, which will lead to larger displacement peak of bridge mid-span.

Key words:concrete-filled steel tubular tied-arch bridge; vehicle-bridge coupled; vehicle speed; vehicle weight; bridge roughness

中图分类号：U446;TU312

文献标志码：A

文章编号：1672-7029(2016)01-0103-08

通讯作者：孙增寿(1963-)，男，河南三门峡人，教授，博士，从事桥梁损伤检测与健康监测研究；E-mail：zengshou@zzu.edu.cn

收稿日期：*2015-06-29