探究规律，巧求坐标

魏秀珍

探究坐标系中点的坐标问题是近几年的热点考题之一，这类题新颖、独特，综合性强，有利于培养同学们的学习兴趣，对提高同学们的解题能力也大有益处.下面举凡例，供同学们学习时参考，

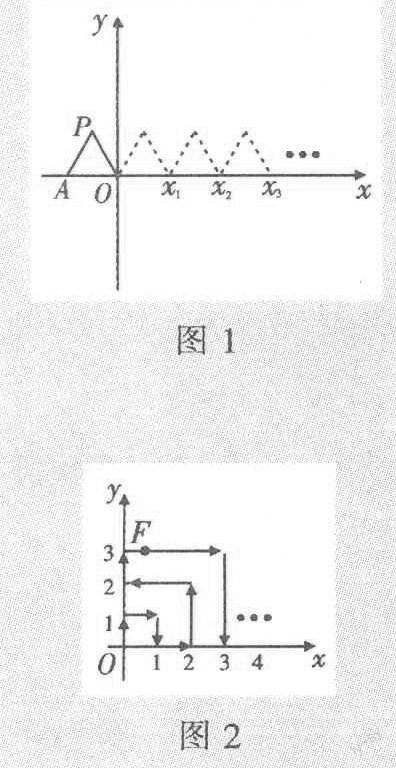
例1 如图1，将边长为1的等边三角形OAP沿X轴正方向连续翻转2015次，求此时三角形落在X轴上右侧顶点X2015的横坐标.

解析：因为等边三角形OAP的边长为1，所以X1的横坐标为1，X2的横坐标为2……

依此得出规律：每翻转一次横坐标就增加1，所以点X2015的横坐标为2015.

例2 -个点F在X轴、y轴上及第一象限内运动，在第1秒，它从原点运动到（0，1），接着按如图2中箭头所示方向运动，其运动方向为（0，0） →（0，1）→（1，1）→（1，0）→……已知点F每秒移动1个单位长度，求第35秒时点F所在位置的坐标.

解析：点F运动方向是（0，0）→（0，1）→（1，1）→（1，0）→……

观察可知对应着x轴上的每个偶数a对应的点，点F运动了a2秒的时间；对应着y轴上的每个奇数b对应的点，点F运动了b2秒的时间.如到（0，1）时，点F运动了1秒，到（0，3）时，点F运动了9秒，所以第36秒时点F所在位置的坐标是（6，0），所以第35秒时点F所在位置的坐标为（5，0）.

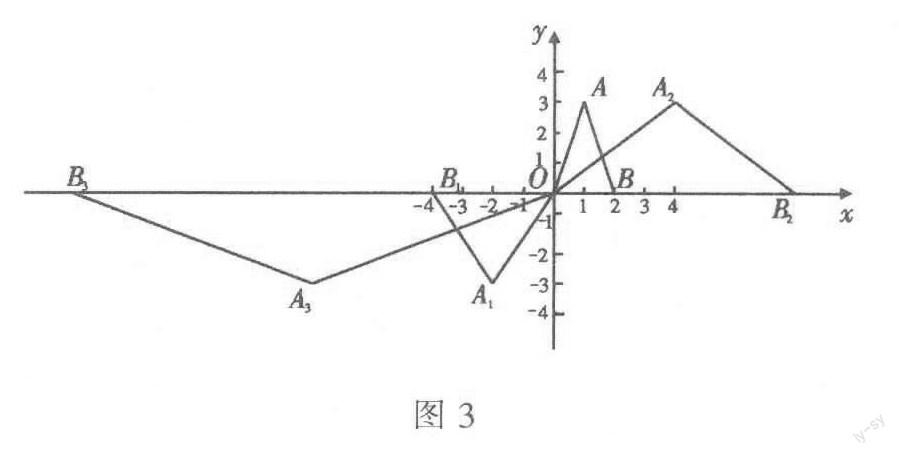
例3 如图3，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3.已知点A（1，3），A1（-2，-3），A2（4，3），A3（-8，-3），B（2，0），B1（-4，0），B2（8，0），B3（-16，0）.

（1）观察每次变换前后三角形的变化情况，找出其中的规律，按此规律再将△OA3B3变换成△OA4B4，则点A4的坐标是____，点B4的坐标是____.

（2）若按（1）中找到的规律将△OAB进行n次变换，得到△OAnBn，推测点An的坐标为____，点Bn的坐标为_____.

解析：（1）根据题意可知，点A4的坐标为（16，3），点B4的坐标为（32，0）.

（2）点An的坐标为（（-2）n，3×（-1）n），点Bn的坐标为（-（-2）n+1，0）.