中职数学践行“慢”教学的策略

【摘 要】基于中职学生的数学基础普遍较弱、学习自信心不足等学情，提出中职数学教师在教学应“慢”点来，适当温习初中所学的知识，帮助学生补牢基础；适度地细讲新学内容，帮助学生掌握要点；适宜地将过程分解得更细一些，帮助学生明了步骤；拿捏好难度，帮助学生增强学习成就感，逐步增强学生的学习自信心和学习效果。

【关键词】中职 数学教学 “慢”策略

【中图分类号】G【文献标识码】A

【文章编号】0450-9889（2015）08B-0082-02

《现代职业教育体系建设规划（2014—2020年）》（教发[2014]6号）明确指出“加强中等职业教育基础地位，强化基础文化和体育、艺术课程”，数学作为中职七大基础文化课之一，其基础地位将会得到应有的重视。然而，中职数学课程教学面临着许多问题，比如，学生的数学基础并不如意，学习起来颇感费力且效果不佳。面对学生的数学学情现状，中职数学教师该如何是好呢？笔者认为面对此状，教师在教學时万不可操之过急，应适当地慢点来，帮助学生一点点、一步步重拾学习自信心、提高学习兴趣和增强学习效果。

一、温习旧知识，基础逐补牢

《论语》有云“温故而知新，可以为师矣”。适当温习初中已学过的数学知识，从一定程度上说是很有必要的，一来可以让学生在温故旧知中补牢基础以便继续往下学习，二来能帮助学生重拾信心以更有兴趣学习后面的内容。笔者在教学实践中，都会在每个班级安排两节课，温习初中知识，效果不错，如以下几个知识点：

1.有理数的运算。特别提示学生自初中引入了“-”号后，在运算时不仅要明确“先乘除、后加减”的规则，而且懂得采取“先符号、后数字”策略进行解答，如（1）-5+（-6）（两个负数的加法，可先确定符号为-，后把两数字5和6相加和为11，故答案为-11；（2）（-2）×（-6）+（-9）÷3（先乘法，这时，可先确定（-2）×（-6）的符号为+，然后再把两个数字2和6相乘，得12，故为+12；除法（-9）÷3中，先确定其符号为-，后数字9除以3得3，故为-3；后由+12+（-3）=12-3=9，故原式=9，并安排学生做适量的相应练习。不少学生开始接受了这种将一个步骤分为“先什么，后怎样”的策略，就觉得很有条理，解答起来也较顺手，心中的迷团得以解开的同时增强了学习的兴趣。

2.合并同类项。如3a-5ab-4a+6ab ，知道 3a与 -4a，-5ab 与+6ab 分别是同类项，合并时“字母不变、系数相加减”，知 3a与-4a 合并为 -a，而 -5ab与+6ab 合并为+ab ，所以原式合并同类项后等于-a+ab 。

（3）移项。如，请将5+x2=7x-5 右边各项都移到左边，知道所移的项为 7x和 -5，移项时强调“被移的项反号”，当然右边两项移走后将“空着”，即为0，于是移项后为 5+x2-7x-（-5）=0，则有 x2-7x+10=0，引导学生明确“被移的项反号”，其他的只字未提，所以无需多事，让他们明确数学学习时“记其要点，无需多事”，引导他们避免再次出现他们之前因自作主张而生发的各种错误。

二、细讲新内容，要点逐记牢

对于新的内容要细讲，当然这里所讲的“细讲”不是指重重复复地讲，而是从多角度或者深入剖析去帮助学生理解和掌握，让学生的大脑跟着思维运转起来，在逐步掌握新知的同时学会如何去学习及思考。笔者在教学实践中，常会采取一些举措来丰富教学内容，将新知讲得较细，效果明显。比如，在讲第一节新课中“集合”这一概念时，先问问学生在什么时候会听到有人喊集合，不少学生都很高兴地答道“军训时，教官会喊”“上体育课时，体育老师也会叫集合”“做早操时，上面的领导也会要我们集合”……再问“听到集合后，你们会怎么样呢？”答“会马上集中过去啊”，让学生明确生活中的“集合”。接着，给出数学中的集合概念“集合——由所有确定的对象所构成的一个整体”后，引导学生去理解这一概念，指出让学生关注“的”字，从而知“集合是一个整体，这个整体有很多对象，这些对象是确定的”，即“集合←整体←对象（确定的）”，如此一来，同学们就能逐层去判知构成一个集合的条件。再者，举例问“14计算机1班所有的同学能否构成一个集合”，有些学生疑惑了，于是按上面的分析问三个问题：“是一个整体吗？”“有对象吗？”“确定吗？”（三问后，统一共识：能），再问“14计算机1班所有高个子的同学能否构成一个集合？”（三问后，统一共识：不能），又问“14计算机1班最高的3名同学能否构成一个集合？”（三问后，统一共识：能）。最后一同看课本上的例题、习题，学生普遍都能准确得出谁是集合而谁不是集合，同时开始关注“的”字了，并在后面学习集合之间的关系时，能通过“的”字，准确判断出集合A={平行四边形}，B={矩形}，C={菱形}，D={正方形}之间的关系。当然，还有不少例子，如在讲集合的交集时，首先，让学生体味成语“百感交集”；然后，让学生观察维恩图来找出两个集合A和B的相交部分，并得知里面的元素既是集合A中的元素，又是集合B中的元素，即它们的公共元素；接着，重点引导学生明确交集的符号开口方向是向下的，理由有两个：文字“交”共分上中下三个部分，其中最上部分“亠”的方向并不唯一、下部分“乂”共有4个方向并不唯一，而中间“八”延长后的开口向下；中国古时结婚拜堂文化“夫妻交拜”，开口方向也向下的；最后，引导学生明确“交集开口方向向下，找它们的公共元素”，据此一起看几道习题，通过实践，学生普遍表示这一知识学得很扎实，都快忘不了了。

三、分化解过程，要领渐掌握

对于中职学生来说，有时并非完全是因为他们的基础太差而无法学下去，有时是因为无法“一步到位”，所以在教学中，不妨引导学生将一些过程进行更进一步地分解，化为多个步骤，并在“熟能生巧”的功效下达成“合一”，进而做到“一步到位”。如此不仅能帮助学生“曲线救国”式地成长，而且逐步增强学生学习的自信心和效果，还能帮助学生养成一些好的学习习惯。

例如，有学生反映不能准确地将数轴上的某一范围表达为不等式或者不能将某一不等式在数轴上表示出其范围。为此笔者在教学时，将它进行了有效分解，下面通过两例来谈。

1.请将数轴所表示的部分写成不等式的形式

首先明确这一范围，共有两个端点-3，5；接着知道在-3处向右跑，故比-3大，又是实心故要取等，则有≥-3；而在5处向左跑，故比5小，又是空心故不取等，则有<5 ；如此一来，范围为 -3≤□<5，中间空白处得补上一个变量，所以这一范围写成不等式的形式，为-3≤x<5 。

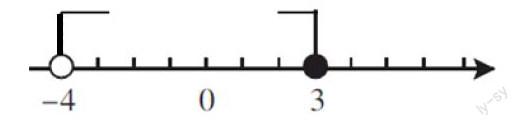
2.请在数轴上将不等式 3≥x>-4表达出来

在讲解完后，不少学生表示“啊，不会吧，就是这么做的呀，一点也不难呢。”“老师，要是早点遇到你就好了，这样的题目一点都不难理解。”在尝试几题后，学生基本都掌握了这一方法。在期末时，笔者测试了他们，不少学生都能在较短的时间内准确地给出答案。

四、拿捏好难度，自信渐拾回

有人提出“降低难度是解决厌学问题的不二法宝”，笔者虽感赞同，但仍持几分怀疑，毕竟一味降低难度并不是解决问题的最有效方法，甚至会妨碍学生的长远成长。笔者在教学中，会根据所教的内容，梯度地设计好难度，先让学生在较易的习题解答中增强信心和成就感，然后乘势而为，适当加大难度，后又增加难度，甚至会讲到高考题，让学生发出“只要我们愿意努力，我们也能学好数学，并可参加高考”的感叹。

例如，在讲到《集合之间的关系》时，笔者就和学生分享了这样一道高考题：

若集合A={x|x=4n+1，n∈Z}， ， ，則A，B，C的关系是（ ）

A. A=B=C B. C∪A=B C. C∩B= A D. B∩C=A

知道，A：x=4n+1，n∈Z ；B：x=4（n-1）+1，n∈Z ；C：x=4（2n）+1，n∈Z ，易知它们的数字部分全是+1，而字母部中同有一个4，“去同”后留下A：x=n，n∈Z ；B：x=n-1，n∈Z ；C：x=2n，n∈Z ，显然n 和 n-1都是整数，2n 是偶数，而偶数一定是整数，但整数不一定是偶数，所以选答案D。

笔者在教学中，会选择难度适当的高考或者中考考题，和学生一起探究解答，他们在成功解出后都会会心一笑，信心渐渐增强起来。

诚然，要想中职学生学好数学，并不是一件容易的事情，更不是一件短期就能成的事情，需要教师花些时间、费些心力，在教学中适当地慢一些，再慢一些，一点一滴、慢慢地引导学生去思考、理解、感悟和尝试，帮助学生在一步一个脚印中取得进步、重搭信心、收获成就感。

【参考文献】

[1]甘志国.数学教学更需要“慢教育”[J].中学数学月刊，2010（03）

[2]高晓兵.中职数学教学改革探析[J].河南教育（职成教版），2014（05）

（责编 卢建龙）