洞悉初中数学考题创设的“玄机”

☉江苏省泰州市孔桥初级中学 田伯青

洞悉初中数学考题创设的“玄机”

☉江苏省泰州市孔桥初级中学 田伯青

考试是当前检查学生学习情况和反馈教师教学效果的重要手段之一，试卷中考题的质量显得十分的重要；新课改要求考题应该在考试大纲的范围内源自于课本教材，而不拘泥于教材；如何创设能够让考生考出“真实水平”的考题是一线教育工作者不断追求的目标，笔者根据自身多年来对初中数学教育教学的实践和研究，采取理论与实际案例相结合的方式，揭示初中数学考题创设的“奥秘”，侧重于介绍优秀考题创设的有效途径与处理策略，从而最大程度地发挥初中数学考题的“异向”作用，为广大初中数学教育工作者提供一点借鉴.

一、紧抓逆向思维，促进初中数学问题的“逆向化”

初中数学概念与运算通常都是成对出现且互逆的，这种对立关系形成思维的可逆性，在初中数学考题的创设中，由正向思维向逆向思维的转变反映数学问题的题设条件与结论进行位置调换，这样正、逆数学问题等价性的不确定也激发学生发挥双向联想的思维冲动，打破思维定势的束缚，形成新的思维方法与策略.

例1在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD与BE相交于点F，如图1所示，其中∠ABC= 45°，试求证：BF=AC.

图1

变式：已知AD与BE是△ABC中 BC与AC两边上的高，且交于点F，存在BF=AC，试求：∠ABC为多少？

评析：例1是课本中常见习题，题设中给定图形，已知的条件和所要求得的结论都是确定好的，学生只要寻找证得△BFD≌△ACD即可完成解题；变式是例1题目的逆问题，要求学生根据题设内容自己思考构思画图及探究结论，这种题目要求学生思维的灵活性较大，由于题设中的条件具有一定的隐蔽性和迷惑性，这给学生带来不小的麻烦，稍微不注意就会出现因疏忽题设条件而导致少解的现象，学生在思考本题时应该考虑图1和图2两种情况，根据△BFD≌△ACD从而得出∠ABC=45°（图1）和∠ABC=135°（图2）.

此类考题可以说是源于课本但是又高于课本，学生只有具备灵活调整自身心理过程方向的能力，才能在推理过程中自如地实现反向思维的转换，在创设逆向联结的基础上，实现正向与反向的融为一体化.

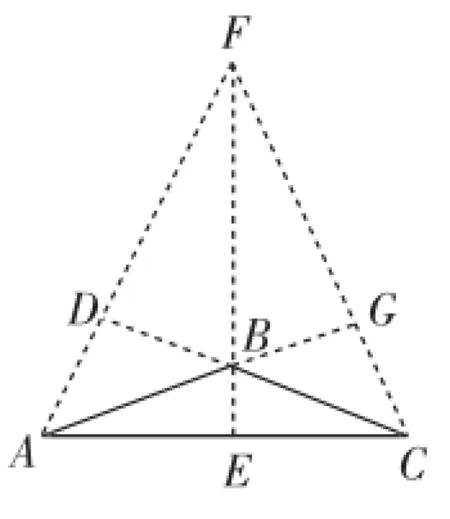
图2

二、注重等价转换，实现原有初中数学题型的“改头换面”

初中数学考题经常会将常见原有题型中的条件或者问题结论，通过等价变换后让题设条件与背景变得具有一定的隐蔽性，难以直接发现其内涵，主要目的是用来考查学生透过表象洞察初中数学问题本质的能力.

例2如图3所示，在Rt△BAC中，AB⊥AC，AE⊥BC，∠C=60°，CD=3，则AB=_________.

图3

评析：将例2中原来题设中的条件进行了等价的转

图4

此类考题创设的目的是为了增强考查学生的思维能力和综合分析能力，让学生感受到考题的似曾相识之感，都能在课本试题中追寻到“原貌”，在处理的过程中，通过对这些等价转化条件的准确辨析，实现“化新为旧、化难为易”，大大提升了数学解题的效率.

三、树立考题“导向性、探索性”意识，助推初、高中数学的有机衔接

科技进步的过程就是人类不断探索与创新的过程，初中数学问题的解决过程具有明显的探索性特征，初中数学探索性问题之所以被命题者所青睐，主要是由于这类题型能够有效地考查学生的创新思维能力与探究能力.

例3已知点P为等腰△ABC中BC边上的任意一点，PD⊥AB于点D，PE⊥AC于点E，CF⊥AB于点F，则存在PD+PE=CF；如果点P在BC的反向延长线上，则PD、PE、CF三者之间的关系如何？

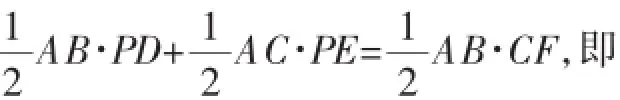
图5

例4已知P为等边△ABC内部的任意一点，且PD⊥BC于点D，PE⊥AB于点E，PF⊥AC于点F，则存在PD+ PE+PF等于此等边三角形的高h；若P在等边△ABC外部，则PD、PE、PF与高h之间的关系如何？

图6

图7

图8

按照同样的探索思路可以发现图8中的面积关系为S△PAB+S△PAC-S△PBC=S△ABC，即PE+PF-PD=h.

例3与例4是两道比较相似的探索性数学问题，一直是考题创设的热点类型，侧重于检测学生对数学知识的理解和运用，从表面上看两道例题具有不同的结论，但是对于高中学生而言就有所不同，由于高中已经接触到“向量”这一利器，当利用向量来表示有向线段后就很容易发现两道例题的结论可以进行统一；可见，此类考题中渗透着初、高中数学知识的有机衔接的气息，体现了运动与变化、联系与转化、对立与统一等辩证唯物主义思想，具有很强的导向性意味和示范性作用.

总而言之，考题的创设是建立在教学大纲要求与课本教材资源相结合的基础之上进行的，在平凡的数学知识考查中制造形式与手段、背景与情境的“奇巧与新意”，在注重考题创设的立意思想的同时，更加注重所创设的考题有助于考查学生在独立思考的前提下创造性地分析与解决问题的能力，从而促进个性化教育、素质教育的快速形成，作为一线的初中数学教师应该在平时的教学实践中不断地思考与探索考题创设的方式与方法，帮助学生不断地总结与反思，从而提升初中学生的数学解题能力.W