对一道经典折叠压轴题的探析与建议*

☉江苏省张家港市第八中学 高东

对一道经典折叠压轴题的探析与建议*

☉江苏省张家港市第八中学 高东

一、问题呈现

题目平面直角坐标系中有一张矩形纸片OABC，O为坐标原点，A点坐标为（10，0），C点坐标为（0，8），D是线段AB上的一点，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处（如图1）有一抛物线y=ax2+bx+c（a、b、c是常数，且a≠0）经过O、C、D三点.

（1）求线段AD的长及抛物线的解析式.

图1

（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动.设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？

（3）点N在抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M、N、C、E为顶点的四边形是平行四边形？若存在，请求出点M与点N的坐标；若不存在，请说明理由.

本题是一道由一张矩形纸片折叠形成的直线型坐标几何问题，综合考查轴对称、全等三角形、相似三角形、矩形的性质、勾股定理与方程、平行四边形等方面的知识.重点考查学生建构几何模型的能力，综合运用数学知识解决综合问题的能力，以及运用方程思想、转化思想、数形结合思想和分类讨论思想解决问题的能力等.试题内涵丰富，解法经典，值得深思.

二、解法探析

1.第（1）问——折在对称，叠在全等，数形结合列方程分析：折叠，实质上是一种翻折变换，即折叠前后重叠部分的对应线段、角相等，对应点的连线被折痕所在的直线垂直平分.从中我们不难看出，折叠后重叠的三角形是全等三角形，其对应边相等，对应角相等.

第（1）问的入口较宽，比较简单，能保证大部分学生会做，只要抓住折叠前与折叠后不变的量.折叠前后哪些量变了，哪些量不变，问题就会迎刃而解.先在Rt△OEC中求出OE长，再在Rt△ADE中运用勾股定理构建方程求AD.然后将O、D、C三点的坐标代入抛物线y=ax2+bx+c，求出a、b、c即可（如图2）.

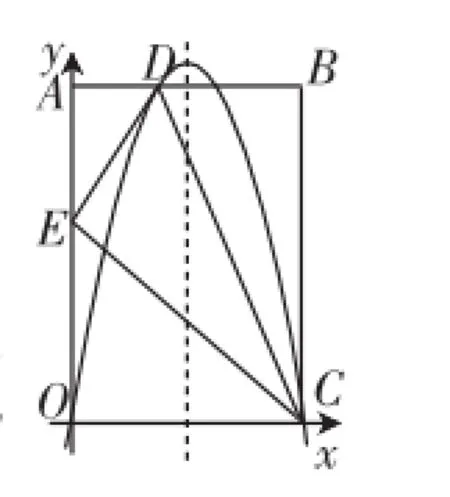
图2

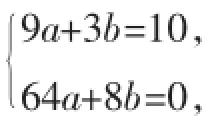
2.第（2）问——线动构相似，几何转代数，分类讨论列方程

分析：相似，语出《易·系辞上》：“与天地相似，故不违.”数学学科解释为：“如果两个图形的形状相同，但大小不一定相等，那么这两个图形相似.”第（2）问属于动态探究问题，解决此类问题的难点是用变量表示线段的长度，关键是模拟运动路线，画出所有符合情况的图形，分类讨论，把几何问题转化成代数问题，根据相似三角形产生的对应边成比例建立含t的方程是求解的关键.分别用含t的代数式表示CQ和CP的长，再利用相似三角形产生的对应边成比例构建含t的方程，求出点的坐标.

解：分类讨论.

情况1：（如图3）当∠PQC=∠DAE=90°时，因为∠DEA+∠OEC=90°，∠OCE+∠OEC=90°，所以∠DEA=∠OCE.

图3

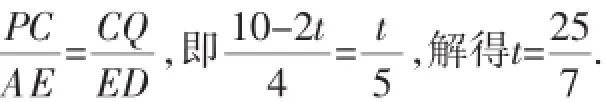
图4

3.第（3）问——平移定坐标，代数转几何，分类讨论求坐标

分析：平移，实质是等距同构，它不改变图形的形状和大小，平移后的图形与原图形上对应点连接的线段平行（或在同一条直线上）且相等.本案例是中考的经典考题，已知两个定点的坐标，设其中一个动点的坐标，以这三个点为顶点，通过平移画出平行四边形，根据坐标平移的性质写出第四个顶点的坐标，最后根据第四个顶点的坐标，判断平行四边形的存在性，并求出点的坐标.

第（3）问情况有两种，点N在EC的上方或下方，所要求的点有六个，符合条件的点有三个，如何条理清晰地进行分类得出点的位置是解题的先决条件.这类问题通常是以任意两点形成的线段为平行四边形的对角线进行分类思考.

解：存在.

图5

情况1：（如图5）当点N在EC的下方时，设点N的坐标为（4，m），此时由题意可知m＜3.过E、C、N三点分

所以当别作NC、EN、CE的平行线，则以E、C、N三点为顶点的平行四边形有三个：以EC为对角线的▱EM1CN；以EN为对角线的▱ECNM2；以CN为对角线的▱CM3NE.下面分类求点的坐标.

①以EC为对角线的▱EM1CN（如图6），求点N，M1的坐标.

图6

②以EN为对角线的▱ECNM2（如图5），求点N，M2的坐标.

③以CN为对角线的▱CM3NE（如图5），求点N，M3的坐标.

情况2：当点N在EC的上方时，设点N的坐标为（4，m），此时由题意可知m＞3.同上方法分类讨论（解法略），可以求出三个m的值，但考虑到m＞3，这三个值不合题意全部舍去.

三、建议与感悟

综观上面的三个问题，呈现一种层层递进的关系.全等、解直角三角形、求抛物线的解析式、相似、平移、列方程、解方程是基础，三角形相似、数形结合、分类讨论是能力的提高，几何转代数、代数转几何彰显数学思想的本质.它的教学是学生积累数学活动经验、感悟数学思想方法、综合基础知识、锻炼数学思维能力的主要手段，教学中教师要结合学生的特点，在学生已有知识的基础上整体把握，逐步推进，在“双基”转“四基”的过程中，让数学思想方法逐步地融入到实际教学中.

1.重视“探、构、列、解”的过程——关注基础，引领方法

《义务教育数学课程标准（2011年版）》（以下简称《课标（2011年版）》）指出：“数学知识的教学，应注重学生对所学知识的理解，体会数学知识之间的关联.”压轴题的整体实现需要基础知识的日积月累和零散知识点的衔接.教师在教学活动中不能生拉硬扯，应努力挖掘其中可能蕴含的基础知识、基本模型、基本数学思想，分析解题方法，而应以理解为基础，并在教学中不断巩固和深化.为了帮助学生真正理解、思考问题，教师应重视“探、构、列、解”的过程，组织学生开展实验、操作、尝试等活动，引导学生进行观察、分析，画出图形，写出推理过程，逐渐提高学生解决问题的能力，帮助学生积累数学活动经验，提高数学素养.例如：第（1）问直角三角形和抛物线模型，其中直角三角形模型解决的思路是将几何问题转化为代数问题，也就是通过勾股定理来列方程，求出线段的长.在教学中教师可以多设计这样的例子，让学生在基础知识的基础上，理解其解题的基本方法，让解题方法引领我们的课堂教学.第（1）问抛物线模型，求解析式通常有一般式、交点式、顶点式三种主要的方法.在教学中教师要根据实际情况，引导学生通过分析理解，合理地选择解题方法，让运算变的更加简单.

2.强调“模型思想”——注重过程，提升能力

《课标（2011年版）》指出：“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径.建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义.”此压轴题设计了直角三角形、抛物线、相似三角形、平行四边形四种常见的几何模型，教师在实际教学中，可以运用几何画板来模拟，让学生根据模拟过程分析画出有可能的情况，搞清楚为什么要这样画草图，然后分类进行讨论，根据图形的基本性质列出方程，不仅要使学生掌握操作的程序和步骤，还要使学生理解其中的道理.例如：第（2）问相似三角形模型和第（3）问平行四边形模型，这两种题型都是中考常见的，教师可以利用几何画板来模拟它们的运动过程，根据几何图形描述图形的运动和变化，让学生直观地分析相似的两种情况和平行四边形的六种情况，依据语言的描述画出草图，求出结果.这些内容的设计有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识.

3.体现“几何转代数、代数转几何”本质——凸显能力，彰显思想

《课标（2011年版）》指出：“借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.”在数学中，平面直角坐标系架起了“数”与“形”之间的桥梁，使我们可以用几何的方法研究代数问题，又可以用代数的方法研究几何问题.例如：第（3）问平行四边形模型，在教学中教师首先可以在对称轴上任取一个点N，这个点的横坐标为4，纵坐标设为m，其中未知数m就是“数”与“形”之间的桥梁，利用几何画板作出平行四边形，求出平行四边形的第四个顶点的坐标，帮助学生直观地理解数学.最后把第四个点的横坐标和纵坐标分别代入抛物线的解析式，在整个教学过程中用到了数形结合、分类讨论、模型思想、几何转代数、代数转几何等数学思想方法.其中，几何直观发挥着重要作用.

总之，经典的中考压轴题是在数学目标指引下，从教材出发，通过对基础的数学知识改编融合而成的，这就要求我们教师重视“探、构、列、解”的过程，强调“模型思想”，引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中发现“变”的规律，体现数学思想方法，从而达到巩固知识，培养能力，提高学生数学素养的目的，达到“不同的人在数学上得到不同的发展”.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.W

*本文为江苏省现代教育技术研究2014年度立项课题《基于现代信息技术的教学有效性研究》的研究成果，课题编号：2014—R—32329.