利用构造法巧解数学中的最值问题

☉陕西省西安市庆安初级中学 刘岚英

利用构造法巧解数学中的最值问题

☉陕西省西安市庆安初级中学 刘岚英

所谓构造法，就是根据题设条件或结论所具有的特征和性质，构造满足条件或结论的数学对象，并借助该对象来解决数学问题的思想方法.运用构造法解决问题，要充分挖掘题设条件和结论的内在联系，把问题与某个熟知的概念、公式、定理、图形联系起来，进行构造，使问题转化，增强问题的直观性.

例1如图1，A、B两地相距600km. AC是笔直地沿东西方向向两边延伸的一条铁路.点B到AC的最短距离为360km，现计划在铁路线AC上修一个中转站M，再在B、M间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍，那么，为使通过铁路由A到M，再通过公路由M到B的总运费达到最小值，请在图中画出中转站M的位置，并求出AM的长.

图1

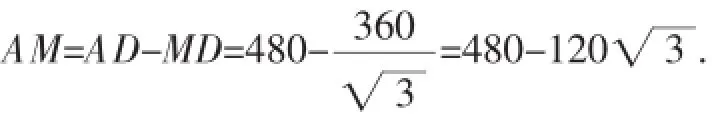
启示：利用直角三角形中30°角所对直角边等于斜边的一半，构造AM与BM共线时的图形解题.

例2在平面直角坐标系中，已知点A（-2，0）、B（0，4），点E在OB上，且∠OAE=∠OBA，将△AEO沿x轴向右平移到△A1EO1，连接A1B、BE1，当A1B+BE1取得最小值时，求点E1的坐标.

分析：如图2，过点A作B1A⊥x轴，使B1A=BE=3，连接A1B1，构造△B1AA1≌△BEE1，则A1B1=BE1.要使A1B+BE1取得最小值，则BA1与A1B1共线，即B、A1、B1在同一直线上.

图2

启示：要求A1B+BE1的最小值，构造A1B与A1B1共线，因为两点之间线段最短.

例3已知点A（0，4）、B（4，1），在x轴上有一动点P，则|PA-PB|的最大值是多少？

分析：如图3，假设x轴上有一动点P，连接PA、PB，则有PA-PB≤AB.

PA-PB最大时，由图知P、A、B三点共线.

则PA-PB的最大值为AB=5.

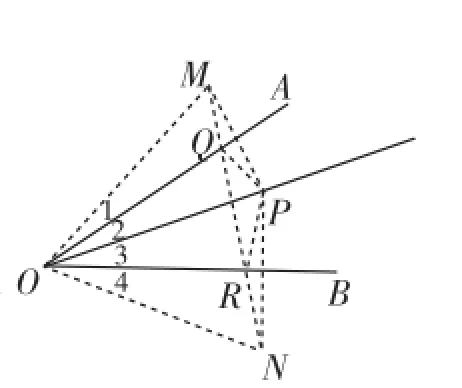
图4

设AA1=m，则

启示：利用三角形两边之差小于第三边，当两边之差等于第三边时，三点共线.

例4如图4，∠AOB=45°，角内有一点P，PO=10，在角的两边上分别有两点Q、R（均不同于点O），则△PQR的周长的最小值是多少？

分析：作点P关于OA的对称点M，连接OM，作点P关于OB的对称点N，连接ON，则MQ=PQ，PR=NR，∠AOB=∠2+∠3=45°.又∠1=∠2，∠3=∠4，则∠MON=2（∠2+∠3）=90°.

启示：利用对称性构造图形.

构造法是求解数学问题的一种重要的方法，在数学学习中，要善于联想、类比、分析、构造，充分利用典型数学模型来解决问题，这样会让陌生的问题变得非常熟悉，提高解决问题的能力.WG