运动之中的常规考量——2014年广东卷中考第25题的思路突破与教学建议

☉广东省东莞市东莞中学松山湖学校 张青云

运动之中的常规考量
——2014年广东卷中考第25题的思路突破与教学建议

☉广东省东莞市东莞中学松山湖学校 张青云

研读2014年广东省中考数学试卷，在保持总体难度稳定平衡的基础上，试卷结构更趋合理，基础知识覆盖面更广，特别是压轴题的设计，一如既往地以动态变化类为基架，突出考查学生在未来数学学习和应用数学解决问题过程中最为重要的核心概念、思想方法和常用的技能，综合性更强，具有较高的信度和恰当的区分度.本文拟对该压轴题展开一些思路探究，并围绕该题的解题教学给出建议，供同行研讨.

一、解题呈现与思路探究

图1

题目如图1，在△ABC中，AB= AC，AD⊥BC于点D，BC=10cm，AD= 8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于点E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为ts（t＞0）.

（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形.

（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长.

（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由.

图2

1.思路探求

（1）两种方法证菱形.

如图2，在已知t值的前提下，可以求得HD的长，得到H为AD的中点，由EF⊥AD，可以有两个不同方向的思考：一是说明EF是AD的垂直平分线，得到AF=DF、AE=ED，再考虑证△AEF为等腰三角形，得AE=AF，从而根据“四条边相等的四边形是菱形”的判定得到结论；二是由EF∥BC、H为AD中点，可以得出E、F分别为AB、AC的中点，再由中位线定理，判断出DE∥AF，DF∥AE，从而由“对角线互相垂直的平行四边形是菱形”的判定得到结论.

（2）二次函数中探求图形面积的极值.

这里的运动型综合问题，涉及动点与动线两种运动对象，如图3，在研究△PEF的面积时，首先是要处理好动线段EF如何表示的问题.这是相似三角形学习时经常会遇到的一个常规问题.在△ABC已知BC及其高AD长的情况下，不难得到EF=10-t，由此可表示出△PEF面积的函数关系式，并进一步求得该函数的极值.

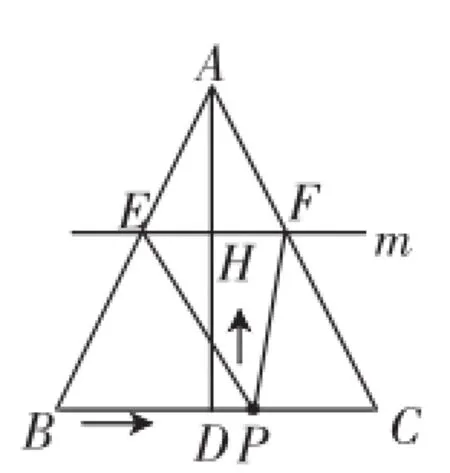
图3

（3）分类讨论显常规.

运动类问题中，多数都以考查分类讨论思想方法为目的，而研究某个三角形变化的形状，可谓是这类问题的一种常规而经典的设计方式.比如，这里研究△PEF为直角三角形，就可以根据三角形三个内角中可能为直角的不同，分三种情况画三个对应图形加以研究分析.

图4和图5这两种情况并不困难，可分别利用相似三角形，得到相关的比例式，从而得到有关t的方程，求得t的值.

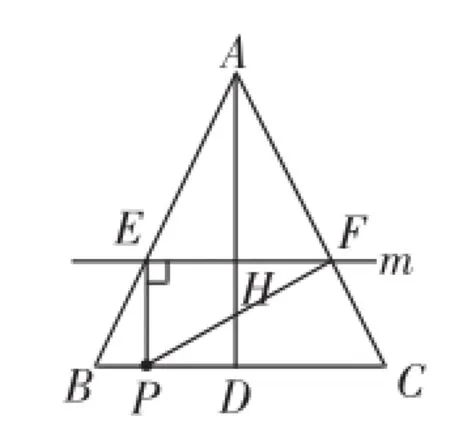
图4

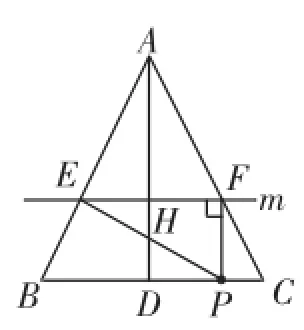
图5

图6

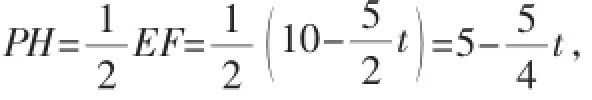
图7

2.参考答案

（1）当t=2时，DH=AH=4，则H为AD的中点.又因为EF⊥AD，所以EF为AD的垂直平分线，所以AE=DE，AF= DF.因为AB=AC，AD⊥BC于点D，所以∠B=∠C.因为EF∥BC，所以∠AEF=∠B，∠AFE=∠C，所以∠AEF=∠AFE，所以AE=AF，所以AE=AF=DE=DF，即四边形AEDF为菱形.

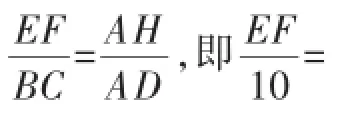
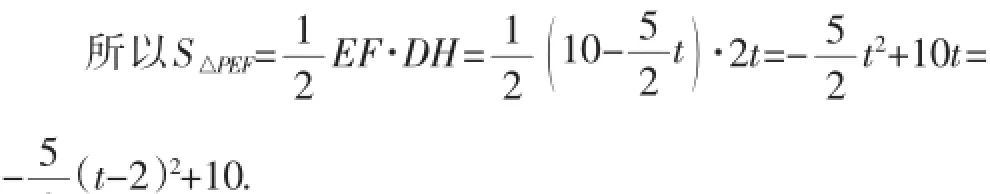
所以当t=2s时，S△PEF存在最大值，最大值为10，此时BP=3t=6.

（3）存在.理由如下.

①若∠PEF=90°，如图4所示，此时PE∥AD，PE= DH=2t，BP=3t.

②若∠EFP=90°，如图5所示，此时PF∥AD，PF=DH= 2t，BP=3t，CP=10-3t.

③若∠EPF=90°，如图7所示，连接PH.

二、教学思考

现在的数学中考在总体难度控制、强调双基的前提下，似乎有一种“简单题目不复习也会，有难度的题目复习了也不会”的尴尬，以至出现有些地方或学校的考生总体平均分偏高，区分度却不强的现象，使试题的效度大打折扣.为什么压轴题会让大家觉得讲了白讲、教了白教呢？除了学生某些方面的因素之外，笔者觉得与教者在备课阶段对解题教学的定位和思考有密切的联系.教者不能仅仅满足于带领学生寻求问题的答案，而更应当引导学生注意解题之后的回顾反思，反思解题中用到了哪些知识？哪些方法？这些知识和方法是怎样联系起来的？是怎么想到它们的？困难在哪里？关键是什么？遇到过什么障碍？后来是怎么解决的？是否还有别的解决方法？命题能够推广吗？……罗增儒教授认为，只有如此不断地追问与反思，才能不断地改进和完善眼前的解题，提炼出对未来解题有指导作用的信息，使理解进入到深层结构.

1.化动为静

运动类问题大都是以动点、动线或者几何图形整体运动为载体的，在分析问题时，首先就要弄清楚运动的相关要素，如运动的对象、方向、速度等，并将这些要素以某种形式呈现出来，使动态的问题，转化为常规的有静态味道的几何图形问题.比如分析本题时，我们首先就要弄明白动点P、动线m的运动方向及运动速度，把动线m的运动加载到动点H上，得到BP=3t、CP=10-3t、DH= 2t、AH=8-2t等，以此为基础，再分析图3或者图4，就使问题显得更为清晰.

2.重视数形结合

运动类问题以运动为表象，其内隐的数学思想主要是分类讨论、数形结合、方程等思想，解题中，我们要特别注意数形结合，根据动态变化的不同状态来展开研究.就本题而言，无论是证明四边形是菱形、研究三角形面积的极值，还是研究三角形的形状，其实都是运动类问题中的常规形式，应当早已在平时的复习训练过程中“覆盖”过若干次的.教学中，我们要特别注意借助于数形结合，引导我们的学生养成将问题切割成若干小问题的意识，有敢于将“母图”分解为若干“子图”的勇气，形成一（小）问题一（子）图的态势.如第（3）问，要引导学生理解，我们的常规策略就是针对直角可能出现的三种情况，果断地将其切割为三个“子问题”，画出三个对应的“子图”，然后由易到难，各个击破.

3.注重利用信息技术动态呈现，突破难点

运动类问题的思维障碍有时就在于分辩不清各种可能出现的情况，因此教学中，教者要引导学生想办法让图形动起来，在动中观察和思考.比如，有些问题是涉及三角板运动的，就可以用三角板的移动来帮助思考等.教师当然也可以采用一些信息技术手段，辅助呈现动态的图形，使学生直观地感知到变化的不同状态，达到理解题意、突破难点、贯穿思路之目的，从而促进他们思维能力的发展与提高.本题第（3）问的教学，我们就可以运用几何画板，直观地呈现动点P和动线m的运动情况，当然我们也可以借助于几何画板测量角度的功能测量相关的角度，或者通过建立相应模型等方式帮助学生理解△PEF，比如，我们过点E、F分别画EF的垂线、并以EF为直径作圆，如图8所示，则只有当点P运动到此虚线模型之上时，△PEF才可能为直角三角形.这些手段，都可以有效地促进学生理解能力的提高.

4.注重变式训练

图8

运动变化类的问题，一定要注意加强变式，以一变多.变式训练是我国数学教育在解题教学中的一个优良传统.罗增儒教授说：“变式练习的作用，首先是通过变换方式或添加次数而增强效果、巩固记忆、熟练技能；其次，是通过必要的实践来积累基本问题，积累理解所需要的操作数量、活动强度和经验体会.”本题的变式，我们可以引导学生向以下几个方面拓展.

（1）当点P运动到点C时，△PEF的面积是多少？（这样的设计，可以使问题从第（1）问的特殊，发展到第（2）问的一般，使两小题形成为一个完整的问题系统.当然，也可以追问图中其他部分的面积）

（2）可以将第（3）问改为“是否存在某一时刻t，使△PEF为等腰三角形？若存在，请求出此时t的值；若不存在，请说明理由.”（对等腰三角形的讨论，也是运动变化类问题中的常规设计，此问三种情况均存在）

（3）将第（3）问改为“是否存在某一时刻t，使四边形EFPB为平行四边形？”（一样的是延续前面存在性设问风格，不同的只是追问其他发生变化的图形部分）

（4）请求出tan∠PEF的值.（在运动过程中，∠PEF的大小其实是保持不变的，这也就是为什么图4不存在的原因，理解了这一点，你就会发现，动点P与动线m的结果，叠加在线段PE中，就使线段PE表现为以点B为位似中心的放大，当我们在几何画板中追踪线段PE时，可以清楚地看到线段PE的变换方式，如图9）

当然，如果愿意钻研，本题也还可以从交换动点P、动线m的运动速度，或者让动线m从A向D运动等来展开研究.

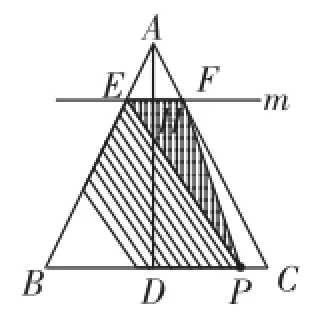
图9

三、写在最后

运动变化类问题是一类对知识的综合程度、能力要求都很高的题型，在惜时如今的考场上，对绝大多数学生而言，当然是一个严峻的考验，这也正是在这样的题型上学生得分率普遍不高的原因所在.但所谓“万变不离其宗”，在面对运动变化类问题时，我们就是要引导学生理解并掌握其中的常规，使万变归“宗”.虽然这并不容易，但它的长期积累会升华为学生出色的数学才华，并促进他们反省思维的生成与发展.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.刘家良.变化的是“形”，未变的是“质”——2014年天津中考卷第25题的评析及教学启示［J］.中学数学（下），2014（9）.

3.浦叙德，谢洁红.从知识整体性视角设计主问题引领课堂教学［J］.中学数学（下），2014（8）.

4.王端祥.从“简洁”视角赏析2014年上海中考卷压轴题［J］.中学数学（下），2014（8）.

5.［美］杜威.我们怎样思维［M］.北京：人民教育出版社，2005.W