单站BDS与GPS实时测速方法研究
2015-05-08汪晓龙王振杰姬生月
汪晓龙,王振杰,姬生月,陈 武
单站BDS与GPS实时测速方法研究
汪晓龙1,王振杰1,姬生月1,陈 武2
(1.中国石油大学(华东) 地球科学与技术学院,青岛 266580;2.香港理工大学,中国 香港 999077)
速度信息与位置信息一样,也是非常重要且应用十分广泛的信息。本文针对传统的GPS测速方法的不足,借鉴时间基线模型的思想,采用时间基线法对BDS和GPS测速进行研究,分别采用了BDS和GPS观测数据进行测试,结果表明:BDS与GPS速度解算结果精度相当,三个方向的测速精度均在亚厘米级,两者数据的融合解算能提高精度;采用广播星历的时间基线法求解的GPS速度与PPP解算的结果差别不大。由于该方法能够同时探测并修复周跳,所以不受周跳影响。
测速;GPS;BDS;时间基线
0 引言
速度信息与位置信息一样,也是非常重要且应用十分广泛的信息,特别是在高精度动态应用中,不仅需要知道运动载体的位置,还要精确确定载体的速度。传统的测速手段主要借助多普勒频移和激光,全球卫星导航系统(global navigation satellite system,GNSS)出现后,为速度的测量提供了一种新的技术手段和实用方法。全球卫星导航系统因其全方位、全天候、全时段、高精度等特性,迅速成为一种主流的定位手段。GNSS测速就是通过安装在运动载体上的GNSS接收机,利用获取的GNSS 信号就可以在进行动态定位的同时,实时地测量载体的运动速度[1]。
目前在测速方面的研究大部分是基于全球定位系统(global positioning system,GPS)的,测速的方法主要有三种[2-3]:利用GPS高精度定位的位置差分获取;采用GPS多普勒频移数据获取;通过载波相位中心差分方法获取。差分测速和差分定位一样,必须选取合适的参考站,随着参考站和流动站距离的增加,GNSS误差的空间相关性减弱,差分方法的精度也随之降低,在大区域或复杂地形的应用中具有一定的困难[4],因此,第一种方法成本较高且不适用大范围区域的测速。许多低成本的GPS接收机不提供多普勒频移数据,因此,第二种方法的应用也经常受到限制。对于第三种方法,受周围复杂环境的影响,特别是载体在高动态运动中,载波相位将很可能会频繁发生周跳,从而影响测速精度[5]。
北斗卫星导航系统(BeiDou navigation satellite system,BDS)作为我国独立运行的全球卫星导航系统,摆脱了对GPS的依赖,并可以与GPS相互兼容、相互补充。然而目前对BDS的测速方法及测速精度研究并不多。
本文针对传统的GPS测速方法的不足,借鉴时间基线模型的思想,采用时间基线法对BDS和GPS测速进行研究,分别采用了BDS和GPS观测数据进行测试,结果表明:与载波相位中心差分测速相比,该方法能够同时探测并修复周跳,即使在复杂不利的观测环境下,也不会受到频繁发生的周跳影响,测速精度依然很高;并且采用单站GNSS接收机进行速度估计具有独立性,不依赖于其他测站,降低了成本;同时该方法无需多普勒频移数据。
1 时间基线法测速原理
1.1 时间基线法测速模型
时间基线法[6-7]来源于时间相对定位模型,也称为时间基线,是近年来提出的用来处理GNSS观测值一种手段。首先在一个已知的测站上进行观测,获得观测数据然后,用户将接收机快速移动到一定距离以外的未知测站上,在移动过程中,接收机连续锁定卫星信号,再在未知测站上进行观测获得数据。这样就可以采用单个接收机在不同时刻不同测站采集观测数据,从而解算出两个测站之间的相对位置。一般要求接收机的采样率要比较高,比如1 Hz。如果将接收机安置在动态载体上,也可以求得该载体的在相邻历元间隔中的平均移动速度。
该方法中采用的载波相位观测值如果发生周跳,也就是相邻两个历元间的模糊度参数发生了变化,则采用该方法求解两测站间的相对位置时,必须求解历元间模糊度的变化参数的整数解之后才能准确解算出两站间的相对位置坐标,这就是时间基线法进行测速的基本思想。
根据GNSS载波相位观测方程式[8],对于相邻两个历元t1和t2时刻的观测值,忽略噪声的影响,分别线性化后得到方程

(1)

(2)
式(1)及式(2)中,A1和A2为线性化后的系数矩阵,X1和X2为坐标改正数,由于BDS是三频数据,所以这里波段数i=1,2,3。
将以上两个方程作差,考虑到相邻历元间的时间间隔比较短,天上卫星的空间几何结构的变化很微小,可认为A1=A2,这里用前一个历元观测方程的系数阵来代替,设为A;而对流层延迟和电离层延迟在相邻历元间的变化很小,可以假设历元间作差后不受大气层对流层延迟和电离层延迟变化的影响;对于多路径效应,虽然最多能达到载波波长的1/4,但是它具有比较强的时间和空间的相关性,因此历元间的多路径效应变化可忽略不计;由于卫星钟比较稳定,所以可以忽略历元间卫星钟差的变化,但相比于卫星钟,接收机钟的稳定性要差很多,所以接收机钟差的变化不能忽略,将其用参数Tr表示,则方程变为
A·ΔX+λi·ΔNi+Tr=ΔLi
(3)
式(3)中,ΔX为相邻两个历元间接收机位置的变化,ΔNi为i波段上的历元间模糊度参数之差,即为周跳的大小,ΔLi为i波段上的历元间载波相位观测值之差。
对于BDS三频数据,假设有n颗公共卫星,则有3n+4个未知数,但载波相位观测方程只有3n个,所以必须引入伪距观测值,该观测方程与载波相位观测方程类似,如式(4)所示。
A·ΔX+Tr=ΔP
(4)
这样就构成具有4n个观测方程的方程组,所以为保证有多余观测,这里要求前后两个历元至少有5颗公共卫星,这样才能通过LAMBDA方法求出历元间模糊度参数之差的整数解,然后将其回代到方程(3)中,进而求解该方程的未知数,得到相邻两个历元间接收机位置的变化,除以历元间隔就可以得到运动载体在两个历元间的平均速度。
时间基线法基于动态高采样率的假设,则历元间单差观测值中的大部分误差很小以至可以忽略不计,且模糊度参数值理应为零,如果发生周跳,模糊度参数的估值就是周跳,所以周跳可作为未知参数加到时间相对定位模型中进行估计,最后再利用估计的周跳值对载波相位观测值进行修复,因此,时间基线法进行测速不会受观测值中周跳的影响。
高度角较低的卫星观测值受噪声影响较大,故观测值的权重可设定为观测卫星天顶角(Z)余弦的平方,即
ω=cos2(Z)
(5)
式(5)为时间基线法的随机模型。
1.2 各项误差的精密模型改正
由于采用的是广播星历,并且是单站观测值,无法通过站间差分消除或者削弱相关误差,因此需要考虑更加精密的误差模型来进行改正,这也是该方法的一个必不可少的步骤。主要的误差改正如下:
1)电离层延迟改正
一般采用双频消电离层组合消除电离层延迟的一阶项影响;
对于BDS三频数据采用电离层延迟参数进行估计;
对于单频数据一般采用电离层模型进行改正。
2)对流层延迟改正
可采用Hopfield、Saastamoinen(需提供实测的气象参数,若用标称气象参数计算精度较差,在一定程度上无法满足广大实时导航定位用户的精度需要)等模型进行改正;映射函数可采用NMF、VMF1、GMF模型;在此基础上,进一步增加对流层延迟估计参数。
3)其他误差改正
其他误差改正包括:相位中心改正、相位缠绕改正、地球自转改正、相对论效应改正和潮汐改正等。
1.3 速度估计流程
采用时间基线方法测速的流程如图1所示。
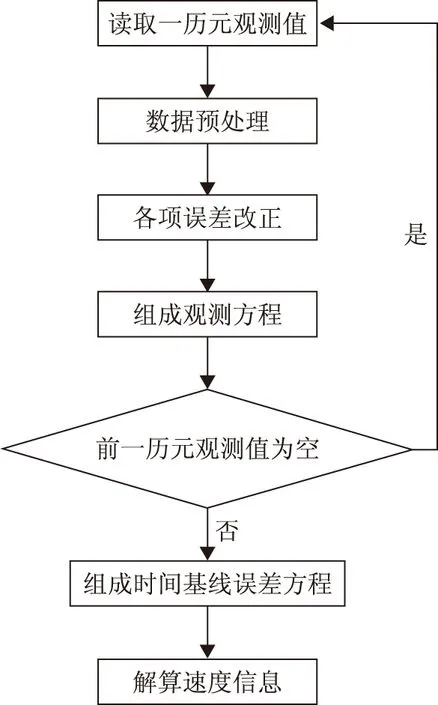
图1 时间基线法速度估计流程图
2 测速实例
为验证时间基线法测速的可行性,首先测试了采样率为1Hz的BDS与GPS的双模静态观测数据,因为静态数据可以认为速度的真值为零,所以可以评定该方法的测速精度;由于该方法主要是应用于运动载体速度信息的获取,本文采用日本311大地震发生时附近的一个IGS站——MIZU站的数据进行了测试,该数据为采样率1Hz的GPS双频数据,并与精密单点定位的结果进行了对比。
2.1 静态观测数据实例
选取2014-03-20前20min的一组实测BDS与GPS双模数据(采样率为1Hz)以及当天的广播星历来模拟实时解算,分别实现了BDS三频观测值、GPS双频观测值、BDS与GPS等权联合求解速度,测速结果如图2至图4所示。

图2 BDS三频测速结果
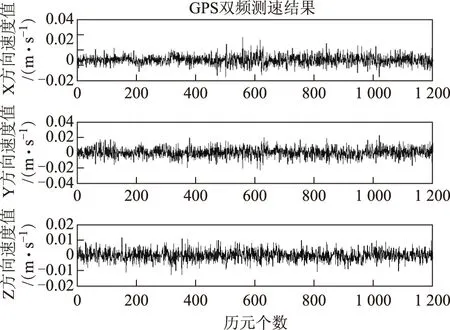
图3 GPS双频测速结果
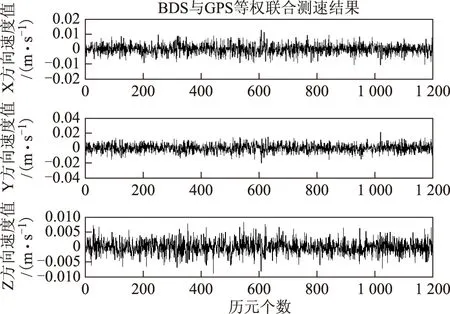
图4 BDS与GPS等权联合处理的测速结果
随后对以上三种情况的结果进行了标准差统计,结果如表1所示。

表1 各方案速度标准差统计/(mm·s-1)
表1中卫星类型分别为:地球静止轨道(geostationary Earth orbit,GEO)卫星,倾斜地球同步轨道(inclined geo-synchronous orbits,IGSO)卫星和中圆地球轨道(medium Earth orbit,MEO)卫星。
2.2 动态观测数据实例
选取日本311大地震震源中心附近的MIZU测站(见图5),观测时段为GPS时间2011年03月11日5时45分之后15 min的GPS双频数据(采样率为1 Hz)进行了测试,测速结果如图6所示。

图5 测站与地震发生的位置示意图
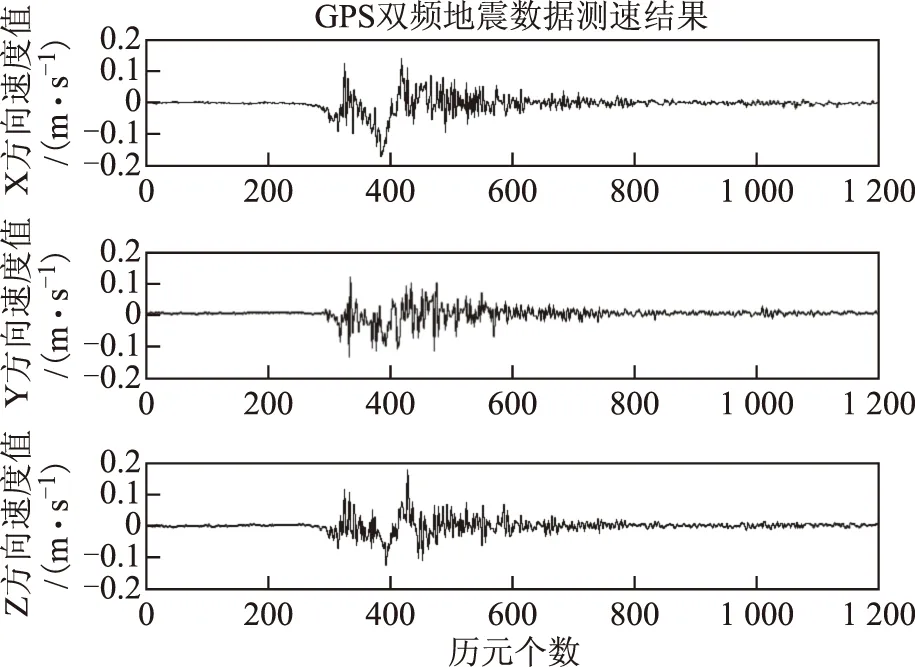
图6 GPS双频测速结果
将速度在时间上累积就得到地震产生的地震偏移,结果如图7所示。

图7 本文方法求得地震产生的测站偏移结果
作为对比,本文引用了加拿大新不伦瑞克省研究学者已经发布的结果。该学者采用了精密单点定位(precise point positioning,PPP )技术进行数据分析,同时还使用高精度GPS卫星轨道和时钟信息,求得大地震造成该地区地理位置的漂移如图8所示[9]。

图8 国外学者发布的测站偏移结果( 解算)
地震动态数据的测试结果显示:地震波传播到MIZU测站的时刻约GPS时间5时47分20秒(即第140历元处)左右;大地震造成日本GPS观测站MIZU站产生向东约2 m、向南约1 m的永久性位移;时间基线法的结果与PPP后处理的结果比较吻合。
3 结束语
针对传统的GPS测速方法的不足,本文借鉴时间基线模型的思想,采用时间基线法对BDS和GPS测速进行研究,分别采用了BDS和GPS观测数据进行测试,结果表明:静态数据显示BDS与GPS速度解算结果精度相当,三个方向的测速精度均在亚厘米级,两者数据的融合解算能提高精度;动态数据方面,采用广播星历的时间基线法求解的GPS速度与PPP解算的结果差别不大,证明了单站实时测速的可行性;随着时间的推移,由于系统误差等的累积效应,位移值偏差会变大,这将是需要进一步研究的工作。
本文采用的方法主要有以下优点:该方法能够同时探测并修复周跳,即使在复杂不利的观测环境下,也不会受到频繁发生的周跳影响,测速精度依然很高;采用单站GNSS接收机进行速度估计具有独立性,不依赖于其他测站,降低了成本;同时该方法无需多普勒频移数据。
速度信息的应用非常广泛,相信的本文的研究将会有助于地震形变监测、地震灾情实时获取、海啸预警、建筑物和大坝等的变形监测等方面的研究。
[1] 杨龙.GPS测速精度研究及应用[D].青岛:国家海洋局第一海洋研究所,2007.
[2] 何海波.高精度GPS动态测量及质量控制[D].郑州:中国人民解放军信息工程大学,2002.
[3] 吴富梅,肖云.利用伪距差分法进行GPS测速[J].武汉大学学报:信息科学版,2010,35(9):1034-1038.
[4]COLOSIMOG,CRESPIM,MAZZONIA.Real-timeGPSseismologywithaStand-aloneReceiver:APreliminaryFeasibilityDemonstration[J].JournalofGeophysicalResearchSolidEarth,2011,116(B11):75-87.
[5] 陈永奇.GPS相对定位中系统误差的影响[J].武汉测绘科技大学学报,1990,15(2):1-9.
[6] 喻国荣.基于移动参考站的GPS动态相对定位算法研究[D].武汉:武汉大学,2003.
[8] 周巍,郝金明,冯淑萍.北斗三频数据周跳的探测方法[J].测绘科学技术学报,2012,29(2):87-90.
[9]GPS世界.GPS数据显示日本仙台大地震 造成明显的地理位置漂移[EB/OL].(2011-03-13)[2015-04-21].http://www.gpsworld.com.cn/1146.html.
Single Station Velocity Estimation:GPS vs BDS
WANGXiao-long1,WANGZhen-jie1,JISheng-yue1,CHENWu2
(1.School of Geosciences,China University of Petroleum,Qingdao 266580,China; 2.The Hong Kong Polytechnic University,Hong Kong 999077,China)
Same to position,velocity is also very important and widely used.In this research,based on time-relative theory,velocity estimation based on BDS and GPS is studied.The numerical results show that the velocity estimation accuracy is mm level and similar for GPS and BDS.The integration of GPS and BDS can improve the velocity estimation accuracy.The relative position change by accumulating the velocity is similar to that from PPP.As the method can detect and correct cycle slip,it will not be affected by cycle slip.
velocity estimation;GPS;BDS;time-relative
汪晓龙,王振杰,姬生月,等.单站BDS与GPS实时测速方法研究[J].导航定位学报,2015,3(3):39-42+55.(WANGXiao-long,WANGZhen-jie,JISheng-yue,etal.SingleStationVelocityEstimation:GPSvsBDS[J].JournalofNavigationandPositioning,2015,3(3):39-42+55.)DOI:10.16547/j.cnki.10-1096.20150308.
2015-05-18
汪晓龙(1989—),男,安徽休宁人,硕士生,主要从事GNSS精密导航与定位研究。
P
A
2095-4999(2015)-03-0039-04
生仁军.GPS载波相位定位中周跳探测方法的研究[D].南京:东南大学,2006.
10.7666/d.y1038419.
