一种区域覆盖遥感卫星椭圆轨道设计方法
2015-05-08沈欣,姚璜,张靖
沈 欣,姚 璜,张 靖
一种区域覆盖遥感卫星椭圆轨道设计方法
沈 欣1,2,3,姚 璜4,张 靖2
(1.地球空间信息技术协同创新中心,武汉 430079;2.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079; 3.武汉大学资源与环境科学学院,武汉 430079;4.华中师范大学教育信息技术学院,武汉 430079)
在航天遥感任务分析与设计过程中,特殊类型轨道(太阳同步轨道、回归轨道等)是卫星轨道设计的重要选择。当前遥感卫星轨道设计研究主要集中于太阳同步、回归的圆轨道设计方面,此类轨道具有全球覆盖、固定重访周期等独特优势,但是,面向热点区域侦察与监控等区域覆盖任务时,太阳同步轨道难以保证对特定目标的高分辨率成像和快速重访。本文针对区域覆盖任务需求,在介绍临界轨道、回归轨道特点基础上,提出了一种椭圆临界回归轨道遥感卫星轨道设计方法,通过引入回归特性定量描述参数,分析了回归系数的影响因素,提出了具有拱线静止特性椭圆轨道的设计流程,并根据区域覆盖要求给出了轨道设计算例,最后椭圆临界回归轨道的特性、适用任务类型进行了分析,算例表明该种轨道可对局部目标实施高分辨率成像,缩短轨道的回归周期,还保证了对同一纬度目标成像时分辨率一致。
遥感卫星;临界回归椭圆轨道;临界轨道;回归轨道;区域覆盖
0 引言
航天遥感作为一种快速获取地表变化的有效手段,已经广泛应用于国土测绘、资源调查、军事侦察、环境监测等诸多领域中。特别是在各类应急响应任务时,可利用卫星遥感快速、重复获取目标区域的变化情况,及时为应急行动提供空间信息保障。卫星轨道是影响遥感卫星数据获取能力的最重要因素。轨道决定了卫星的位置分布,制约着光学遥感卫星对目标成像的地面分辨率、成像幅宽;此外,由于卫星运动和地球自转,卫星轨道影响着遥感卫星对地覆盖的时序分布规律(如时间分辨率等)。研究光学遥感卫星轨道的优化设计是提高卫星数据获取能力和数据质量的重要途径,对解决遥感数据的按需获取问题具有重要意义。
近地轨道设计方面,国内外学者提出了一些基于轨道动力学理论的轨道设计原则:文献[1]针对低轨卫星轨道设计要求,归纳分析了轨道设计的主要准则和权衡策略;文献[2]提出通过评估交点周期和轨道半径实现全球覆盖的遥感卫星轨道设计方法;文献[3]提出了针对重复轨道覆盖要求的循环覆盖轨道的设计方法。在遥感卫星最常用的太阳同步轨道设计方面,文献[4]对资源一号的轨道设计思路做了全面论述,该星采用了太阳同步、回归、冻结轨道;文献[5]提出了一种遥感卫星太阳同步轨道的快速设计方法,重点分析了太阳同步轨道卫星的地面轨迹的分布和轨道高度衰减的规律;文献[6~7]等在轨道六要素的基础上,给出了在轨道交点周期、回归圈数、回归周期、重复周期和其他因素等约束条件下太阳同步轨道设计的要点;文献[8]通过对太阳同步轨道和回归轨道特性的分析,建立了回归系数Q与太阳同步回归轨道参数之间的数学关系;文献[9]提出了设计了基于优化交点周期的对地侦察卫星太阳同步回归轨道;文献[10]分别对CCD遥感卫星和分布式星载干涉SAR两种遥感卫星的轨道设计进行了研究,提出了满足敏感地区信息快速获取和重访的CCD遥感卫星轨道设计方法。
从以上分析可以看出,当前遥感卫星轨道设计研究主要集中于太阳同步、回归的圆轨道设计方面,此类轨道具有全球覆盖、固定重访周期等独特优势,但是,面向热点区域侦察与监控等区域覆盖任务时,太阳同步轨道难以保证对特定目标的高分辨率成像和快速重访。本文针对区域覆盖任务需求,在介绍临界轨道、回归特殊轨道特性和选择原则基础上,提出了一种椭圆临界回归轨道遥感卫星轨道设计方法,通过引入回归特性定量描述参数,分析了回归系数的影响因素,提出了具有拱线静止特性椭圆轨道设计方法和设计流程,并对轨道的特性进行了分析和总结。
1 回归轨道与临界轨道
1.1 回归轨道
回归轨道是星下点地面轨迹经过一段时间后重复出现的轨道,对遥感卫星而言,这种轨迹周期性重复的特性对提取变化信息是十分有利。
卫星星下点运动轨迹实际上是地球自转、轨道面进动和卫星运动的合成。卫星连续两次升轨(降轨)经过赤道时,相邻的轨迹在赤道上的经度差Δλ为

(1)

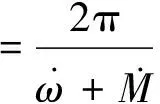
(2)
顾及摄动的影响时
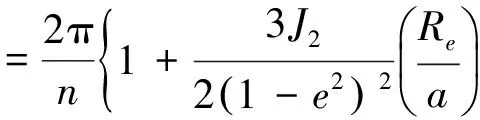
(3)
式(3)中,Re为地球赤道半径,a、i分别为卫星轨道长半轴和轨道倾角,n为卫星运动平均周期。恰当选择轨道的长半轴、倾角、偏心率,使轨道周期满足R·Δλ=2π(R为正整数),卫星在运行R圈以后,地面轨迹与第一次重复,此时回归周期为一天。
若选择轨道的长半轴、倾角、偏心率,使轨道周期满足R·Δλ=X·2π(R、X为正整数),卫星在运行R圈以后,地面轨迹与第一次重复,此时回归周期为X天。回归轨道设计的重点在于确定回归系数Q,本文将对此进行详细的讨论。
1.2 临界轨道
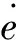
若考虑J2、J3摄动影响下,近地点幅角、偏心率的变化率为

(4)
(5)
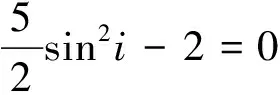
1.3 临界回归轨道
临界轨道具有拱线静止的特性,能保证卫星在同一地区获得的影像的分辨率一致,有助于同源遥感影像的时序分析。临界轨道需满足倾角i=63.43°或i=116.57°,卫星无法实现全球覆盖,但对于高时间分辨率的区域覆盖具有很强的实用价值。采用临界回归轨道,将近地点置于需要侦查目标(或区域目标中心)上空,提高目标成像的空间
分辨率。
2 临近回归椭圆轨道设计流程
2.1 回归系数Q选择
回归轨道满足R·Δλ=X·2π,卫星在回归周期N天运行R圈以后完成一次回归。记
(6)
式(6)中,Q为卫星的回归系数,ωe为地球自转角速度。通常Q为分数,由整数部分和分数部分组成:I、C、N均为正整数,C、N互质且C 1)Q为整数: 卫星轨道的回归周期为一天(N=1)。即卫星在一天内运行Q整圈后,星下点第1圈轨迹与第Q圈重合。以Q=15为例,如图1: 图1 回归系数(1) 2)Q为分数: 卫星的回归周期取决于N,C决定了卫星星下点轨迹移动的方式。 以Q=15.2为例,详细说明回归系数Q与轨道回归特性的关系,此时C=1,N=5,如图2。 图2 回归系数(2) 卫星经历5 d时间,卫星运行76圈时,星下点轨迹与第1圈重合。从图2中可知,在卫星连续两次轨迹的经度差Δλ内(D1N1~D1N2),等间隔插入了后续4 d卫星的第1圈轨道,从左至右一次为第5天第1圈(D5N1)、第4天第1圈(D4N1)、第3天第1圈(D3N1)、第2天第1圈(D2N1)的卫星轨迹。即5 d回归的轨道,Δλ被等分为N个区域,间隔为 (7) 式(7)中,γ为回归轨道的基本间距。回归轨道的基本间距实质上描述的就是在一个重复周期内任意相邻轨迹之间的距离。 2.2 临界回归椭圆轨道设计流程 卫星轨道设计的目标是根据任务需求和约束条件,确定卫星的轨道参数,包括轨道倾角i、轨道长半轴a、偏心率e、近地点幅角ω,升交点赤经Ω。临界回归椭圆轨道设计流程为: 1)确定轨道倾角i; 2)采用式(8),根据任务目标的纬度δ、轨道倾角i确定轨道的近地点幅角ω; sinδ=sinω·sini (8) 3)根据任务分辨率要求和成像载荷特性,确定近地点高度hp; 4)据近地点高度hp、远地点高度ha和轨道长半轴a、偏心率e的关系,加入远地点高度约束(或任务分辨率下限),确定轨道长半轴a和偏心率e的范围为 (9) 5)根据e的取值范围,确定回归系数Q的取值范围。由式(6),回归系数可表示为 Q= (10) 针对备选的Q值范围,确定若干个互质的N、C的组合形式。首先确定N的取值范围并适当选择C,用分数C/N拟合中确定的回归系数Q小数部分,形成若干备选方案; 6)根据升交点地方时计算升交点的赤经,确定轨道的升交点赤经; 7)对每个备选方案的目标要求满足情况进行检验,根据任务需求特点进行折中、选择。 对椭圆轨道遥感卫星而言,近地点位置的选择主要考虑地面分辨率、数据下传等因素。传感器等条件确定的情况下,轨道高度越低分辨率越高。因此,椭圆轨道区域覆盖卫星一般将近地点位置选择在重点区域上空,保证对重点目标的高分辨率覆盖。 任务要求:某光学成像卫星,要求对中心坐标位于(N25.5°,E120.0°)的目标实时高分辨率侦察,要求分辨率为0.5 m,其他区域分辨率优于2 m;回归周期不长于5 d,要求采用顺行轨道。传感器参数:等效焦距f=2 000 mm,像元大小5 μm,等效像元个数16000个。卫星首次对目标侦查时地方时为10:30:00,当前世界时2012-07-01 T 02:30:00。 1)确定轨道倾角i=63.43°; 2)由式(8),近地点幅角ω=28.77°; 3)近地点分辨分辨率0.5 m时,要求近地点高度hp为200 km;远地点处地面分辨率优于 2 m,要求远地点高度ha≤800 m; 4)要满足式(9),要求e≤0.043 6; 5)由式(11),得到e在[0.000 1,0.043 6]范围内时,回归系数Q的取值范围在15.362 2~16.447 7,对应长半轴a的取值范围在6 578.1 km~6 878.1 km,其长半轴与回归系数的关系图(3)所示: 图3 临界回归轨道长半轴与回归系数的关系 6)因要求回归周期小于5 d,故要求N最大值为5,最小值为1。分别用分母5,4,3,2,1构造位于Q取值范围内的分数,共10种组合方式。 7)分别由上述10种备选方案的N、C、Q,计算出对应的长半轴、偏心率和远地点、近地点地面分辨率,如表1。可以看出1、4、8号方案分别在回归周期和远地点分辨率这两个指标上优于其他方案,可作为备选方案,其中1号方案的回归周期为1天,特别适宜于重点目标详查任务。 表1 临界回归轨道备选方案 满足任务要求的临界、回归轨道设计结果如下表所示: 表2 临界回归轨道设计结果 通过对轨道特性分析,能够看出临界回归椭圆轨道适用于区域覆盖任务,能够对局部区域的热点目标实现高时间和空间分辨率覆盖。临界回归椭圆轨道具有以下两个主要优势:1)分析上述算例可知,临界回归椭圆轨道能够实现热点目标固定的高时间、空间分辨率覆盖。通过组合设置轨道倾角和近地点幅角,使得卫星近地点位于目标上空,从而提高对热点目标成像的空间分辨率;第二,在时间分辨率方面,由于回归系数Q主要取决于长半轴的选取,使用了椭圆轨道使得轨道长半轴a的取值范围与回归圆轨道相比有了大幅的扩展,响应扩大了回归系数Q的取值范围,能够实现短周期的轨道回归;此外,与圆轨道相比,椭圆轨道卫星其大部分时间是运行在靠近远地点端,可减少卫星受近地空气阻力的影响,使得卫星具有更长的工作寿命。临界回归椭圆轨道的不足之处在于,由于倾角受限其成像的纬度范围与近极地轨道相比要小,无法实现全球覆盖。 本文提出了一种满足局部区域覆盖要求的具有高时、空分辨率,且具有良好拱线静止特性的临界回归椭圆轨道设计方法。该轨道的主要优势:第一,通过将近地点置于热点区域上空,可保障对局部目标实施高分辨率成像;第二,扩展了回归系数的区间,可大大缩短轨道的回归周期,提高卫星的时间分辨率;第三,由于使用临界轨道,具有良好的拱线静止特性,保证了对同一纬度目标成像时分辨率一致,有利于影像时序分析。随着小卫星技术的快速发展,椭圆临界回归轨道有望成为快速响应卫星轨道设计的热点,提高遥感卫星的按需数据获取能力。 [1] TAINI G,PIETROPAOLO A,NOTARANTONIO A.Criteria and Trade-offs for LEO Orbit Design[C]//Aerospace Conference,2008 IEEE.Big Sky,MT:IEEE,2008:1-11. [2] ZAYAN M A,ELTOHAMY F.Orbits Design for Remote Sensing Satellite[C]//Aerospace Conference,2008 IEEE.Big Sky,MT:IEEE,2008:1-9. [3] 杨维廉.资源一号卫星轨道:理论与实践[J].航天器工程,2001,10(1):30-43. [4] 朱仁璋.卫星循环轨道与覆盖轨道的设计[J].宇航学报,1984(3):22-29. [5] 于绍华,杨林娜.对地观测卫星太阳同步轨道的快速设计方法[J].上海航天,2002(2):5-7. [6] 陈洁.冻结轨道卫星轨道设计与控制方法研究[D].长沙:国防科技大学,2004. [7] 陈洁,汤国建.太阳同步卫星的轨道设计[J].上海航天,2004(3):34-38. [8] 曲宏松,张叶,金光.基于Q值选取的太阳同步回归轨道设计算法[J].光学精密工程,2008,16(9):1688-1694. [9] 廖炳瑜.太阳同步回归轨道的设计、仿真研究[D].北京:中国科学院,2003. [10]谢金华.遥感卫星轨道设计[D].郑州:解放军信息工程大学,2005. A Elliptical Orbit Design Method of Remote Sensing Satellite for Regional Coverage Task SHENXin1,2,3,YAOHuang4,ZHANGJing2 (1.Collaborative Innovation Center of Geospatial Technology,Wuhan 430079,China; 2.State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079,China; 3.School of Resource and Environmental Sciences,Wuhan University,Wuhan 430079,China; 4.School of Educational Information Technology,Central China Normal University,Wuhan 430079,China) Special types of orbit,such as sun-synchronous orbit,regressive orbit,are the first choices for low-orbit optical remote sensing satellite.Currently design of remote sensing satellites orbit focuses on the sun-synchronous regressive circular orbit,which has a unique advantage of global coverage,fixed revisit period.However,when orient to reconnaissance and surveillance mission for specific area,sun-synchronous is difficult to guarantee high-resolution imaging and rapid re-visit.Aiming at regional coverage mission requirements,a critical regressive elliptical orbit (CRE orbit) design method is proposed in this paper.Firstly,the characteristics and selection principles are briefly introduced;then by introducing a regression coefficient Q and analyzing the quantitative relationship between Q and orbit elements,design flow of CRE orbit is introduced;Thirdly,a calculation example of CRE orbit design is put forward based on proposed method;Finally,the characteristics of CRE orbit and its application task is discussed,the example shows that this kind of orbit can ensure the local targets high-resolution imaging,shorten the revisit period with a short revisit period,also maintain the uniformity of imaging resolution for the targets located in the same latitude. remote sensing satellite;critical regressive elliptical orbit;critical orbit;regressive orbit;regional coverage 沈欣,姚璜,张靖.一种区域覆盖遥感卫星椭圆轨道设计方法[J].导航定位学报,2015,3(3):100-104.(SHEN Xin,YAO Huang,ZHANG Jing.A Elliptical Orbit Design Method of Remote Sensing Satellite for Regional Coverage Task[J].Journal of Navigation and Positioning,2015,3(3):100-104.) 10.16547/j.cnki.10-1096.20150320. 2015-05-18 中国博士后科学基金资助项目(2014M562006)、湖北省自然基金项目(2015CFB330)、武汉大学自主科研项目(2042014kf0059,2042015gf0013)、测绘遥感信息工程国家重点实验室专项科研资助。 沈欣(1981—),男,博士后,湖北孝感人,主要从事遥感卫星轨道与成像任务规划研究工作。 P236 A 2095-4999(2015)-03-0100-05


3 临界回归轨道设计算例


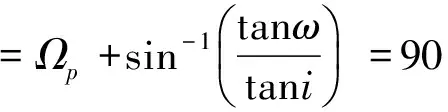

4 临界回归椭圆轨道特性分析
5 结束语
