数形结合思想在中学数学中的应用研究
2015-04-29叶旭丹
叶旭丹
摘 要:文章主要研究了数形结合思想方法在学习数学中的应用,以提高学生数学的能力,培养学生的创新精神。
关键词:数形结合;创新精神;触类旁通
中图分类号:G633.6 文献标志码:A 文章编号:1008-3561(2015)33-0073-02
一、引言
可以说数形结合思想贯穿于整个中学数学的学习过程中,在七年级学习的数轴与实数成一一对应关系中,学生初步体会了数形结合的思想方法;在八九年级的反比例及一二次函数的学习及运用函数的思想求方程的解、求不等式的解集中,学生初步理解了数形结合的思想方法;在高中的幂函数、指数函数、对数函数、三角函数等基本初等函数的学习中,学生对它有了进一步的理解;在解析几何的学习中,让学生深刻体会其本质是用代数方法研究图形的几何性质,反过来用图形去解决代数中的问题,体现了数形结合的重要数学思想。
二、数形结合思想的含义、表现形式
(1)数学思想的认识是对数学知识本质的认识,是数学中的精髓之一。只有重视培养学生对数学思想的认识,才能学会活用知识,达到促进迁移的效果;思想要以知识为载体,知识要以思想为活化剂,知识要通过思想去理解、去激化、去构建,没有思想,知识是空洞的,没有活力的,也是没有意义的。然而令人遗憾的是,在数学教学过程中,很多教师并没有对思想方法的重要性引起足够的重视,还是传统的教学思想,注重对知识的传授,而忽视了知识发生过程中数学思想的渗透,导致一些学生对知识无法举一反三、触类旁通。由此可见,做好数学思想方法的教学,可以让学生轻松快乐地学好数学,提高学生数学的能力,更能培养学生的创新精神。中学数学蕴含着很多的数学思想,如数形结合思想、转换化归思想、分类讨论思想、方程与函数思想、类比联想思想、集合思想、归纳推理思想、抽象概括思想等,抓住突出这些基本思想,就相当于抓住了中学数学知识的本质和精髓。
(2)“数”与“形”是数学的两大基本概念,然而它们之间又是相辅相成的。著名数学大师华罗庚先生写了一首诗: 数与形,本是相倚依,焉能分作两边飞;数无形时少直觉,形少数时难入微;数形结合百般好,隔离分家万事休;切莫忘,几何代数统一体,永远联系切莫分离。法国数学家拉格朗日认为,只要代数和几何分道扬镳,它们的进展就缓慢,它们的应用就狭窄;但当两门科学结合成伴侣时,它们就互相吸取新鲜的活力,就可以快速的步伐走向完善。这里的“数”是指数量关系,“形”是指空间形式。数与形是数学中的两个最基本的概念。数学的内容和方法都是围绕对这两个概念的提炼、演变、发展而展开的。数学科学的发展,形与数常常是结合在一起的,内容上相互渗透的,方法上相互联系,在一定条件下相互转化的。数学史表明,早在数学的萌芽时期,人们计算长度、面积、体积,就把数与形联系在一起了。我国从北宋到元代前期,系统地引进了几何问题代数化的方法,用代数式描述某些几何特征,把图形中的几何关系表达成代数式之间的代数关系。17世纪上半叶,法国数学家笛卡尔通过引入坐标系,建立了数与形的联系,创立了解析几何学。之后,几何学中许多长期没有解决的问题,如著名的尺规作图中的“立方倍积”“化图为方”“三等分已知角”等三大问题,最终都借助于代数方法得到彻底解决。在我们的解题中,也有过这样的体会,有些代数题用图解法助解,常使人顿开茅塞,突破常规思维,使思维进入新的境界。有些平面几何题,利用数量表示线段或角的大小后,可以巧妙地在纷繁的头绪中辟出捷径,收到事半功倍的效果。数形结合还可以使形象思维与抽象思维协同作用,从而使复杂问题简单化、抽象问题具体化,化难为易。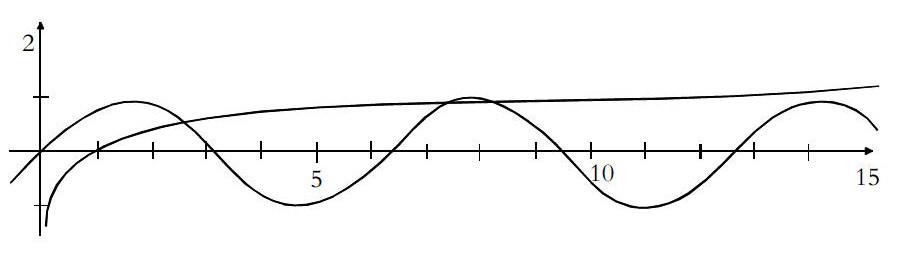
(3)数形结合的途径。1)转化。在遇到抽象的数学问题感到酥手无策时,我们可以尝试涉及概念的图像表示,探索数量关系赋予的几何特征,思考数学问题背后隐含的几何意义,用直观形象支撑抽象思维。如|x-a|?b的几何意义是数轴上两个数x和a所表示的点之间的距离小于等于b,而当x表示变数时,则表示数轴上到的a点的距离小于或等于b的动点的全体。
【典型例题】:例1:求方程sinx=lgx实解的个数。
分析:由于此题是一个超越方程,若用常规代数解方程的方法,显然难于解答,但只要把y=sinx和y=lgx的图像画在同一坐标系中,原方程解的个数问题转化成两个函数图像交点个数问题,答案一目了然。说明:本题充分利用了“数”背后“形”的特征,采用数形结合的解题策略。由本题可见,涉及超越方程问题时,借助函数图像是一个常可尝试的念头。
2)构造。数形结合的思想方法,除了通过转化,把符号语言“翻译”为图像语言,寻求问题背后的几何意义外,另一种重要途径是探求问题隐含的几何模型,这就是构造。如自然会联想到平面内(x1,y1),(x2,y2)两点的距离。
典型例题:例2:已知a,b,cR+,求证:++?(a+b+c)。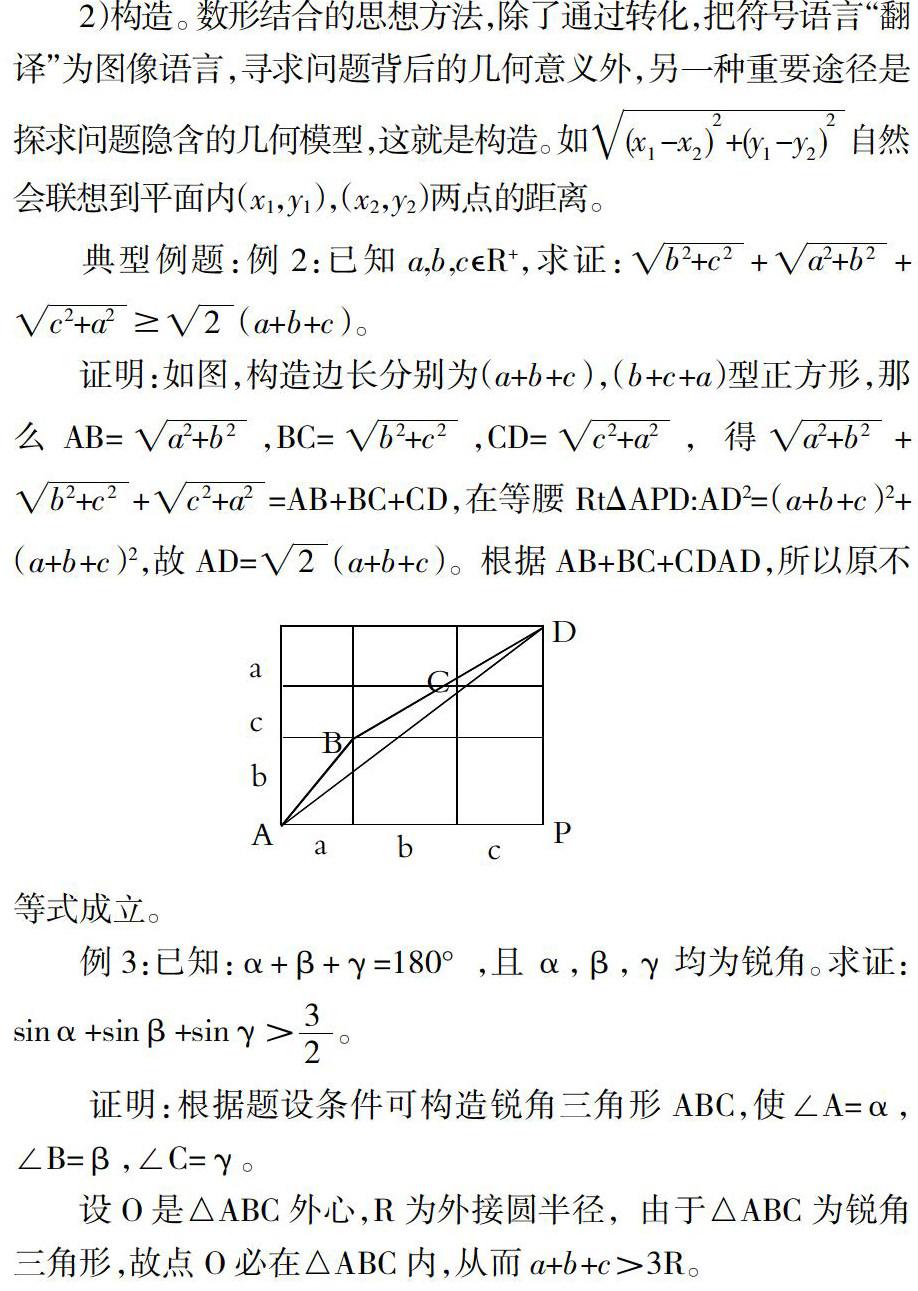
证明:如图,构造边长分别为(a+b+c),(b+c+a)型正方形,那么AB=,BC=,CD=,得++=AB+BC+CD,在等腰RtΔAPD:AD2=(a+b+c)2+(a+b+c)2,故AD=(a+b+c)。根据AB+BC+CDAD,所以原不等式成立。
例3:已知:α+β+γ=180°,且α,β,γ均为锐角。求证:sinα+sinβ+sinγ>。
证明:根据题设条件可构造锐角三角形ABC,使∠A=α,∠B=β,∠C=γ。
设O是△ABC外心,R为外接圆半径,由于△ABC为锐角三角形,故点O必在△ABC内,从而a+b+c>3R。
由正弦定理知:a=2Rsinα,b=2Rsinβ,c=2Rsinγ,∴sinα+sinβ+sinγ>。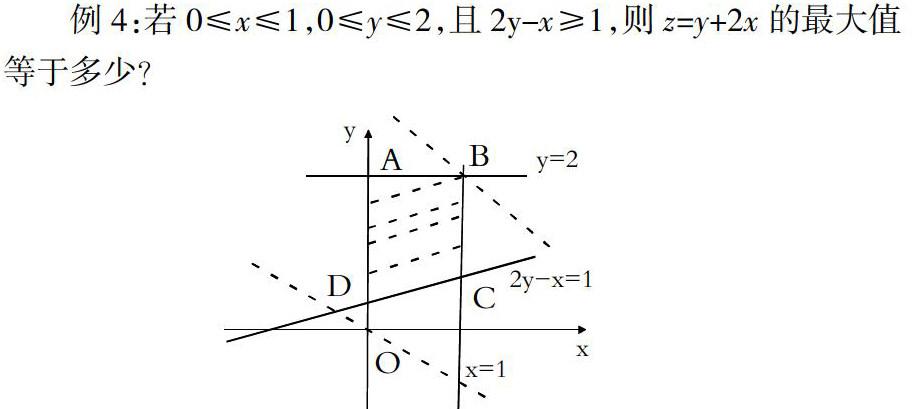
说明:此题把三角问题转化为几何中三角形中的边角关系问题,使解此问题简单易行。
3)坐标法。坐标系的建立是中学数学学习的一个转折点,能使初等数学进入数形结合阶段,并在两个相反方向上进行应用:一方面把几何问题转化为代数问题,通过代数结论获得几何结论;另一方面也可以把代数问题转化为几何问题,通过几何结论获得代数结论。
例4:若0≤x≤1,0≤y≤2,且2y-x≥1,则z=y+2x的最大值等于多少?
分析:先根据约束条件画出可行域,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y过可行域内的点B时,从而得到z最大值即可。
解:先根据约束条件画出可行域,设z=2x+y,最大值为y轴上的截距的最大值,当直线z=2x+y经过区域内的点B(1,2)时,z最大,最大值为4。故答案为:4。
说明:本题主要通过建立坐标系,运用平面区域来表示二元一次不等式组,通过图像获得目标函数的最值问题。
三、结束语
在数学教学中要贯彻数形结合的教学原则,以形数结合的观点深入专研教材,理解数学中的有关概念、公式和法则,掌握形数结合进行分析问题和解决问题的思想方法。
参考文献:
[1]田万海.数学教育学[M].杭州:浙江教育出版社,2002.
[2]李冬胜.数学思维方法[M].太原:山西人民出版社,2010.
[3]王宪昌.数学思维方法[M].北京:人民教育出版社,2002.
[4]张乃达.数学思维教育学[M].南京:江苏教育出版社,1990.
