复杂结构部件概率疲劳寿命预测方法与模型

谢里阳*,任俊刚,吴宁祥,钱文学

东北大学航空动力装备振动及控制实验室,沈阳 110819

复杂结构和零部件的几何形状及受力状态决定了其多部位损伤(MSD)特征,即一个结构部件或一个复杂机械零件上存在多个可能发生失效的关键(高应力/低强度)部位。由于结构和零部件载荷及各部位强度的不确定性,复杂结构和零部件上各损伤部位的疲劳寿命都具有明显的随机性。因此,复杂结构和零部件的寿命并不等于确定性意义上最薄弱部位的寿命,其失效及概率寿命预测问题是一个系统的失效及可靠性问题。若结构或零部件上任一部位失效都会导致整个结构或零部件失效,则一个结构或一个零部件就是一个串联系统。在这样的系统中,若载荷具有不确定性,则各关键部位失效会存在统计相关性,需要有适用的模型预测系统寿命及其概率分布。

近年来,多部位损伤问题得到了极大关注,相关研究包括多裂纹结构的剩余强度问题[1-2]、寿命问题[3]、结构完整性问题[4]等。有许多文献研究了多部位损伤结构的疲劳寿命预测理论与方法[5-12],但多数研究都是在确定性框架下进行的,或只涉及简单的概率计算。

关于疲劳寿命的概率分布问题,传统上多根据P-S-N(应力-概率寿命)曲线预测简单零件(只含有一个可能失效的部位)在确定性的循环载荷作用下对应于一定可靠度的疲劳寿命,或借助应力-强度干涉模型反映载荷不确定性对疲劳失效概率的影响[13-14]。应用应力-强度干涉模型的前提是获得对应于某一寿命的疲劳强度概率分布[15],这样的方法应用难度很大,且适用范围有限。

变幅载荷历程下的疲劳失效概率问题更加复杂,相关研究多局限于具体零件或结构[16],且很少涉及多部位损伤问题。Petryna等[17]研究了钢筋混凝土结构的概率疲劳损伤建模问题,Karadeniz[18]介绍了一种海洋工程结构谱载荷疲劳寿命不确定性分析程序。Kliman[19]介绍了一种基于能量准则估算随机载荷作用下零件可靠寿命的方法,应用S-N曲线和循环应力-应变曲线、载荷历程的标准差和概率密度分布、以及由雨流计数法得到的载荷循环谱块。其失效准则是从能量的观点进行考虑,累积损伤临界值为载荷幅值的函数。文献[20]提出了一个系统可靠性分析的一般方法。本文基于系统失效概率分析及具体损伤部位的概率累积损伤计算,建立多部位损伤结构和零部件概率疲劳寿命预测模型。

1 疲劳失效概率表达方法

指定循环应力水平下的疲劳寿命是一个随机变量,通常可以用Weibull分布或对数正态分布描述。多级谱载或变幅应力历程下的疲劳寿命分布可能表现出更为复杂的形式。为了预测零部件在变幅载荷历程下的概率寿命,首先需要研究变幅应力历程下的疲劳损伤的概率特性,以及概率疲劳损伤累积方法。为了便于处理变幅应力历程下的概率疲劳损伤累积问题,本文首先研究变幅载荷历程下疲劳损伤及其临界值概率分布的表达式,以及与随机临界损伤对应的损伤累积计算方法。

传统损伤累积模型只涉及确定性量,即确定性的寿命和确定性的应力循环次数。在寿命N为随机变量的情形,损伤n/N也为随机变量,n为应力循环次数。若沿用传统的累积损伤临界值概念,认为损伤临界值为1,即损伤临界值为确定性量,失效判据可表达为

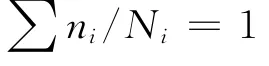
式中:ni为第i应力水平下的应力循环次数；Ni为相应的寿命随机变量。

相应地,失效概率为

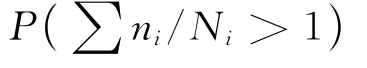
若要应用此式预测疲劳失效概率,需要计算n/N大于1的概率,因而需要确定n/N的概率密度函数。这样做的困难是,难以由寿命N的概率密度函数推导出损伤n/N的概率密度函数。为了避免这样的困难,本文首先探讨变幅应力作用下疲劳失效概率计算的可能方法。为此,需要分析疲劳损伤累积计算中涉及到的有关变量,尤其是有关确定性量与随机变量之间的联系。

在指定循环应力水平si下,寿命为随机变量,其中值和标准差分别为¯Ni和σi,概率密度函数为fi(N)。当应力循环次数为ni时,失效概率为

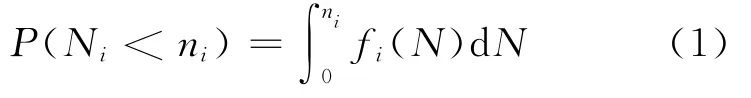
为了便于进行不同应力水平下应力循环次数的损伤等效转换及进行概率损伤累积,可以进行确定性应力循环次数与寿命随机变量之间的概率等效变换。具体作法是,为了便于进行失效概率计算,把原本是随机变量的寿命Ni转换为确定性量,数值为其中值¯Ni；相应地,把应力循环次数转换作为以实际循环次数ni为中值的随机变量,记为nri。对于寿命概率密度函数可用三参数函数(例如三参数 Weibull分布)表达的一般情形,把概率密度函数为fN,i(N)=fN,i(βN,ηN,γN)的寿命随机变量转换为以其中值为具体数值的确定性量,把原本确定性的应力循环次数转换为以其实际循环数为中值,概率密度函数为fn,i(n)=fn,i(βn,ηn,γn)的随机变量,且有P(nri＞¯Ni)=P(Ni＜ni)成立,即

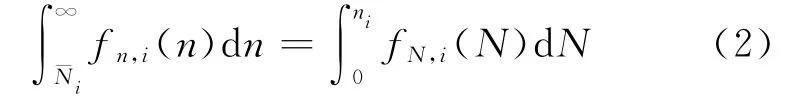
为了实现这样的转换,需要首先以寿命中值为基准,构造寿命概率密度函数的镜像函数,再将此镜像函数向左平移一段距离-ni,即可得到对应载荷循环数的概率密度函数。图1展示了转换前后的情况。

显然,既然可以实现这样的转换,也就可以以寿命中值为基础、以对应的等效应力循环次数随机变量为根据计算概率损伤,把损伤临界值取为确定性量(取值为1)；或以寿命中值为基础、以实际的应力循环次数(确定性量)为根据计算“中值”损伤,把损伤临界值解释为随机变量N/。这样,就可以把累积损伤随机变量与确定性的累积损伤临界值1之间的关系转换为确定性的“中值”累积损伤与累积损伤临界值随机变量之间的关系。

在随机变量(例如对数寿命、对数应力循环数)服从正态分布的情形,为了保证失效概率计算的等效性,应使随机化后的应力循环数的对数的标准差等于该应力水平下寿命对数的标准差σi,即ln nri的中值(均值)和标准差分别为ln ni和σi。

在这种变换的基础上,对损伤临界值可作如下处理。由于寿命Ni为随机变量,应力循环ni次时损伤为随机变量ni/Ni,损伤临界值为¯Ni/¯Ni=1。进行应力循环次数随机化转换之后,相应的损伤随机变量为nri/¯Ni,损伤临界值同样为¯Ni/¯Ni=1。由此可见,疲劳损伤随机变量既可以根据实际应力循环次数以寿命随机变量为基准计算,也可以根据等效的应力作用次数随机变量以寿命中值为基准计算。

从损伤临界值的角度,在某一指定幅值的循环应力作用下的失效概率可表达为

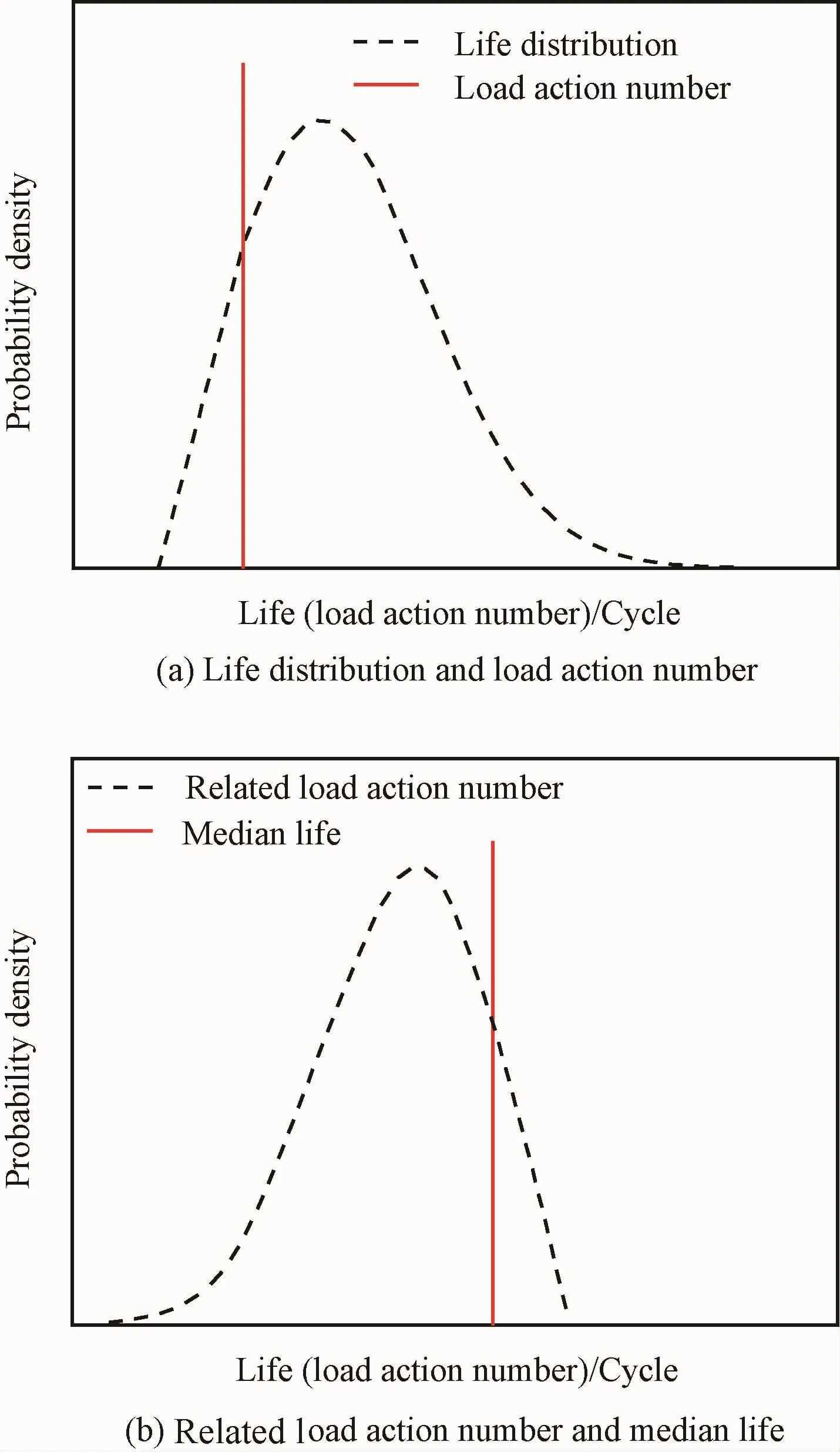
图1 寿命分布与对应应力循环次数分布变换原理Fig.1 Transform principle of life distribution and equivalent load action number distribution

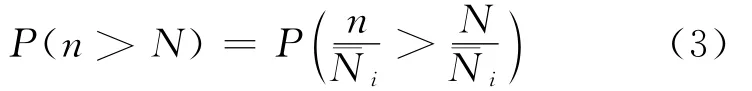
由于n/¯Ni定义为中值损伤,根据式(3),累积损伤的临界值为随机变量。在传统的、确定性意义上的线性累积损伤法则中,损伤临界值(确定性量)与应力水平无关,因而才可以简单地进行累积损伤计算、简单地判定失效何时发生。要建立概率累积损伤法则,也需要清楚概率意义上的损伤临界值随机变量与应力水平之间的关系。只有在损伤临界值的概率分布与应力水平无关的前提下,才能建立像传统累积损伤法则那样形式简单的公式。

定性地讲,在寿命概率分布方面,一般规律是低应力、长寿命对应于较大的寿命分散性。对于损伤临界值的概率分布来说,分散性较大的寿命随机变量除以较大的寿命均值,使得损伤临界值的分散性不会像寿命分散性那样直接与应力水平有关。下面将证明,若不同应力水平下的疲劳寿命Weibull分布的形状参数相同(这是一种很常见的合理假设),则不同应力水平下的损伤临界值的分布相同,即与应力水平无关。

若在任一应力水平下寿命均服从Weibull分布,则在基准应力水平其概率密度函数和累积概率分布函数分别为

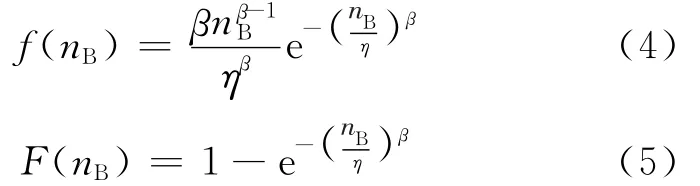
式中:nB为基准应力水平下的寿命；β为形状参数；η为尺度参数。

损伤临界值为

式中:下标B表示基准应力水平。

根据确定随机变量函数概率分布的基本原理,可以得到损伤临界值的概率密度函数和累积概率分布函数分别为

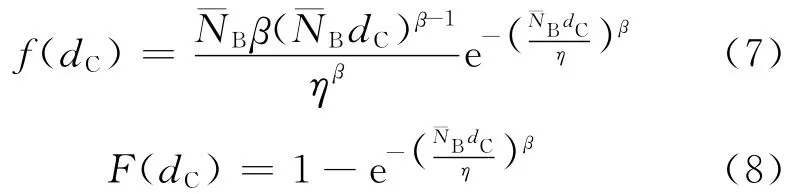
式中:dC为损伤临界值变量。将Weibull分布中值寿命表达式代入式(8),有

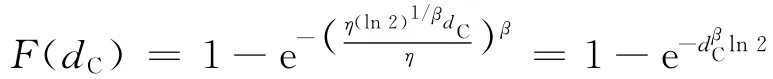
显然,在β为常数(不随应力水平变化)的条件下,损伤临界值的概率分布与应力水平无关。

由于损伤临界值的概率分布与应力水平无关,可以以任一应力水平(例如S-N 曲线所覆盖的应力范围的中间值)下的寿命分布为基准,根据此基准应力水平下的寿命概率分布确定累积损伤临界值的概率分布。或者根据加权计算确定基准应力水平,即对载荷历程进行计数,结果划分为m个应力水平,其中应力si下有ni个载荷循环,则基准应力水平取为

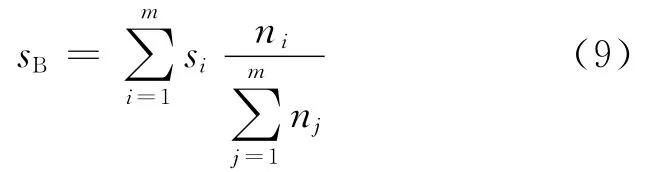
典型寿命分布fN(n)～W(2,200 000)及相应的累积损伤临界值分布概率密度函数fD(dC)如图2所示。考察寿命分散性是否对损伤临界值的概率分布有明显影响,图3所示的寿命分布与图2所示的情形相比有更大的分散性,即其概率密度函数fN(n)～W(1.5,300 000)及相应的累积损伤临界值分布fD(dC)更分散。可以看出,虽然与图2所示的情形相比,寿命分布有明显不同(形状参数、尺度参数都不明显相同),但损伤临界值分布的差异并不是很大。这也定性地支持了损伤临界值分布对应力水平不敏感的观点。

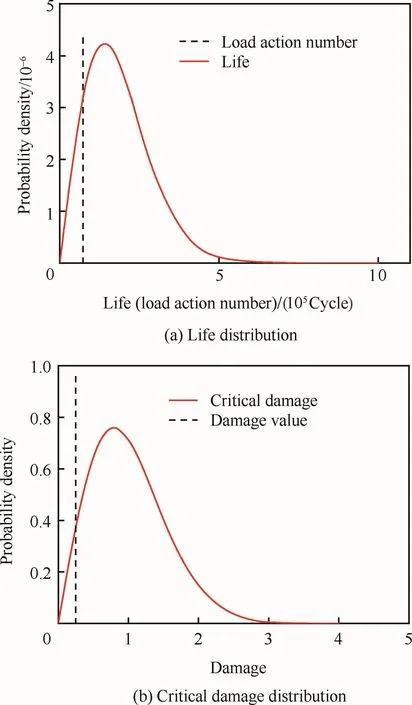
图2 分散性较小的寿命分布与损伤临界值分布Fig.2 Life distribution with small dispersion and critical damage distribution

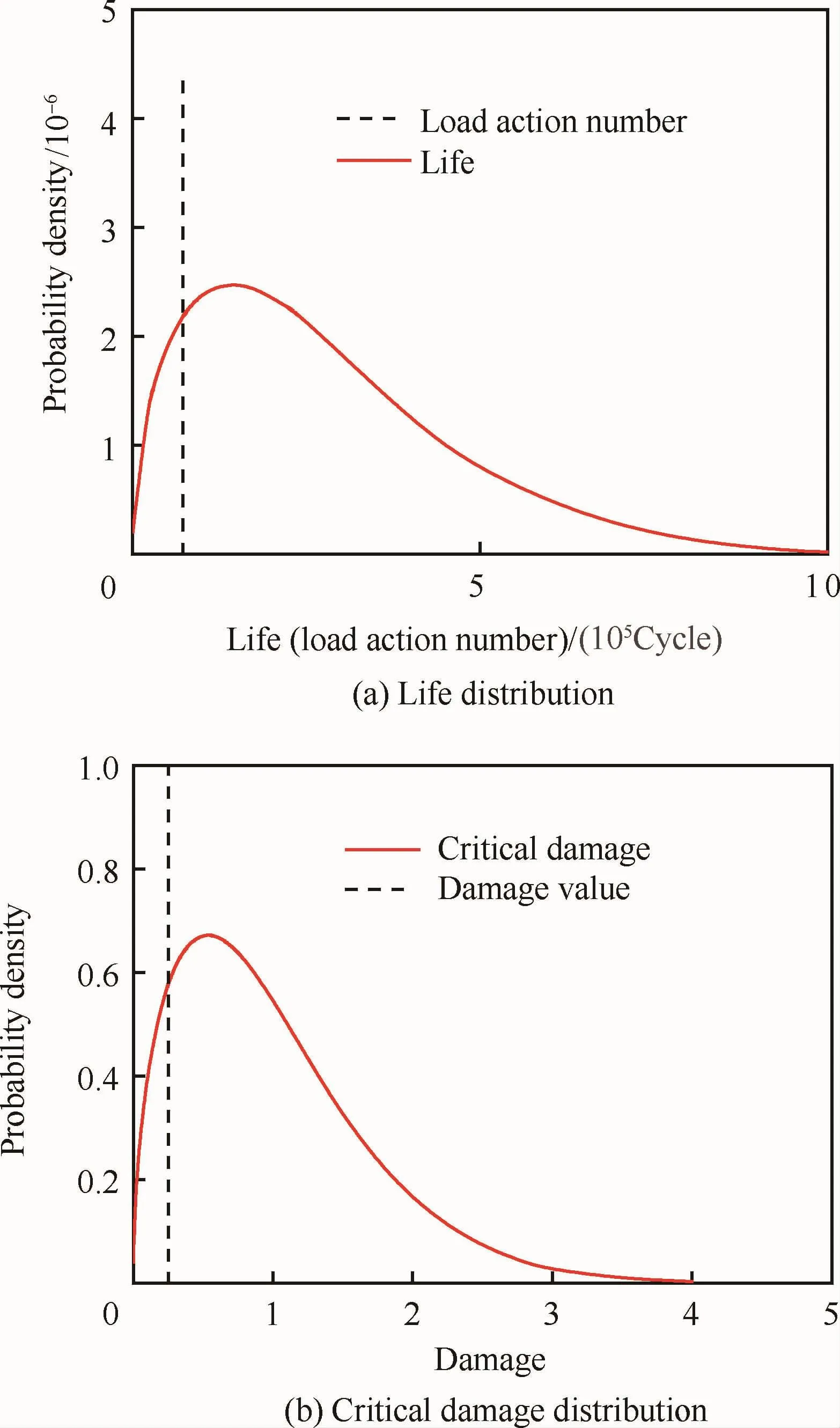
图3 分散性较大的寿命分布与损伤临界值分布Fig.3 Life distribution with large dispersion and critical damage distribution

2 概率累积损伤法则

传统的累积损伤问题只涉及确定性意义上的累积损伤,是在寿命与应力循环数都为确定性量的条件下定义的。由于寿命为随机变量,对应于一定应力水平、一定循环次数的循环应力产生的损伤也是随机变量。从材料性能的角度,也可以认为材料所能容许的损伤临界值为随机变量,即一批材料试样中,相对好的试样能承受更多的应力循环数,而每个应力循环产生的损伤是一定的,只与应力水平有关,与材料性能无关。为了获得概率寿命或可靠寿命,需要建立概率累积损伤法则。疲劳累积损伤法则的基础是不同应力水平的循环应力产生的疲劳损伤存在等效性。概率累积损伤法则的一个必须满足的条件是,不同应力水平下,相同的损伤须对应相同的疲劳失效概率。

根据第1节的阐释、分析与证明,在进行疲劳损伤累积与概率寿命预测时,可以根据寿命中值计算疲劳损伤及进行损伤累积(称为中值损伤及中值累积损伤),根据中值累积损伤与累积损伤临界值的概率分布计算概率寿命——这就是本文要建立的概率累积损伤法则的基本思想。

以不同应力水平下寿命中值为根据折算不同应力水平下的等损伤应力循环次数,即应力sj下的nj个循环产生的疲劳损伤相当于应力si下的ni个循环产生的疲劳损伤,则有

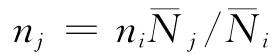
基于损伤临界值分布与应力水平无关的性质(或假设),可知

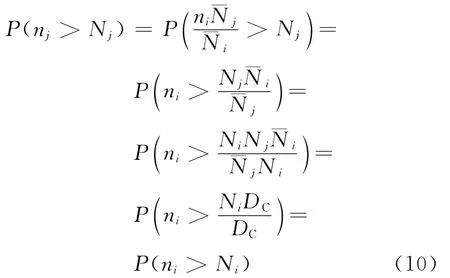
即基于寿命中值折算的不同应力水平下的等效应力循环次数满足“相同的损伤导致相同的失效概率”的原则(或称限制条件):

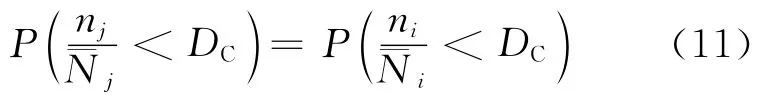
所以,有变幅循环应力作用下的疲劳失效概率计算公式,即概率损伤累积准则:

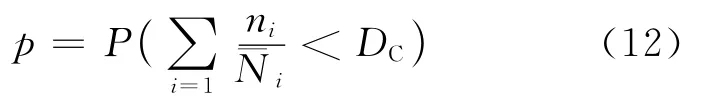
该法则可表述为,变幅应力作用下的失效概率等于以寿命中值为基准计算的线性累积损伤值小于临界损伤随机变量的概率。

3 变幅循环载荷历程下多损伤部位结构概率疲劳寿命预测

在变幅载荷历程作用下,多损伤部位结构上,各损伤部位的应力历程不同,损伤演化历程也不同。设某结构上含有m个损伤部位,所承受的载荷历程i(结构可能承受不同的载荷历程)由应力水平分别为si,1,si,2,…,si,ni的ni个载荷循环构成,损伤部位j(j=1,2,…,m)的应力历程为,,…

根据线性累积损伤计算公式(Miner法则),以各应力水平下寿命中值为基准计算的损伤部位j的累积损伤(即中值损伤)为

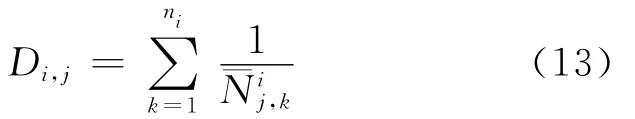
式中:ni为载荷历程i中所含的载荷循环数；为应力幅为的恒幅循环应力作用下结构上j个损伤部位材料的寿命中值。

在该载荷历程作用下,损伤部位j的失效的概率为

根据串联系统概率运算法则,含有m个损伤部位的结构件的失效概率为

考虑到载荷历程的不确定性,令载荷历程i出现的概率为pi,可以根据全概率计算原理计算失效概率,即需要把式(17)扩展为

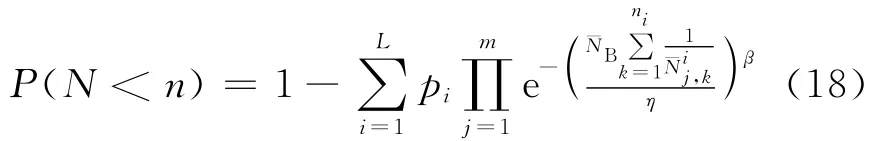
式中:L为载荷历程样本数。

4 应用举例

复杂结构部件上通常包含多个可能失效的关键部位。由于各关键部位的载荷及材料性能存在随机性,一个复杂结构部件相当于一个由多个单元构成的串联系统。因此,对于概率寿命预测而言,多损伤部位结构或机械零部件需要作为一个串联系统对待。由于同一结构或零部件上各部位的应力是由同源载荷产生的,在载荷及材料强度都具有随机性的场合,各损伤部位的疲劳损伤或疲劳寿命在统计学意义上既不完全相关,也不相互独立。因此,多损伤部位结构或零部件的疲劳寿命及可靠性既不能按一个最大损伤部位计算,也不能根据传统的串联系统可靠性模型计算。

图4所示为承受拉伸载荷的带有5个孔的490 mm×180 mm的板状零件。显然,该零件上有10个易损伤部位,即各孔边应力集中处。由于材料性能分散性的原因,即使在相同的循环应力作用下,各易损部位的损伤演化也会有显著差异。

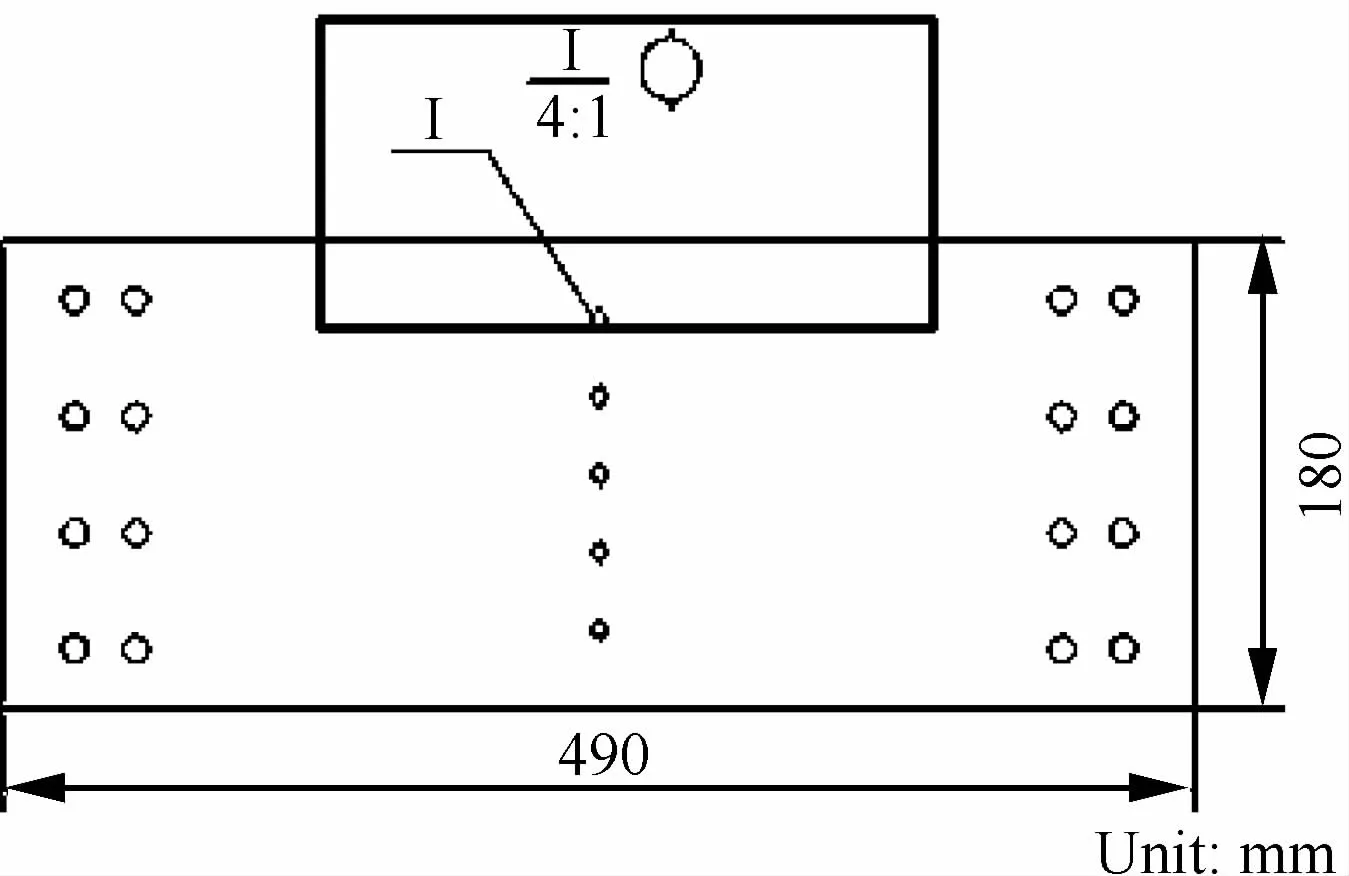
图4 多部位损伤结构Fig.4 Multi-site damage structure

令各损伤部位的应力历程相同。应力历程用应力幅值序列表示,该序列由400～500之间均匀分布随机数构成,图5所示为该循环应力历程的前20个应力循环。

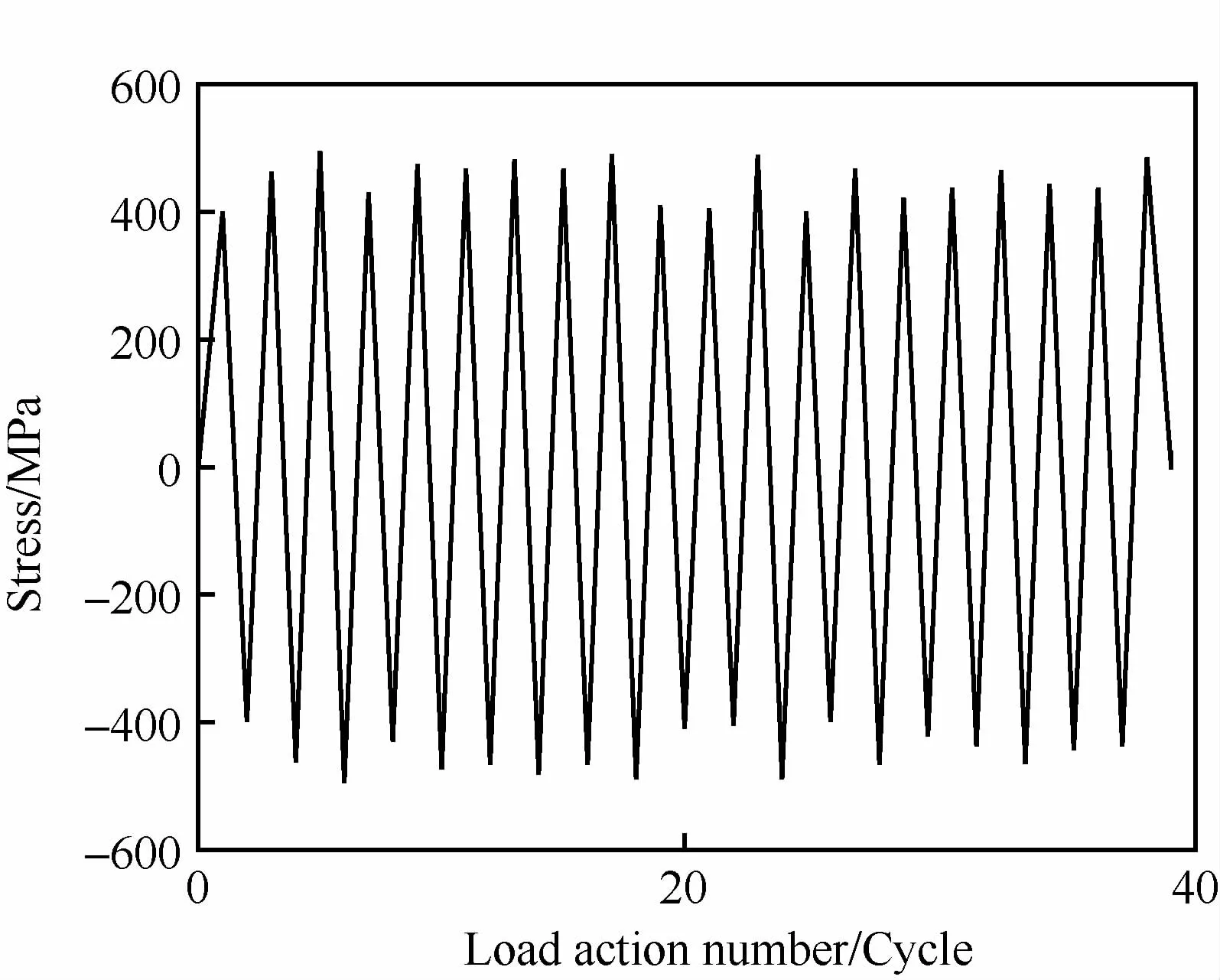
图5 预测寿命用的应力历程(部分)Fig.5 Load history used to fatigue life prediction(part)

令材料的应力-概率寿命性能数据如下:

材料的中值S-N曲线方程为

指定应力水平下的寿命服从Weibull分布,且分散性与应力水平无关。在基准应力水平(450 MPa)下,寿命概率密度函数为

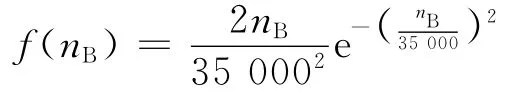
对应于基准应力水平的循环应力作用下疲劳寿命中值为

根据本文介绍的累积损伤计算方法,容易得到累积损伤与载荷循环之间的关系,如图6所示。

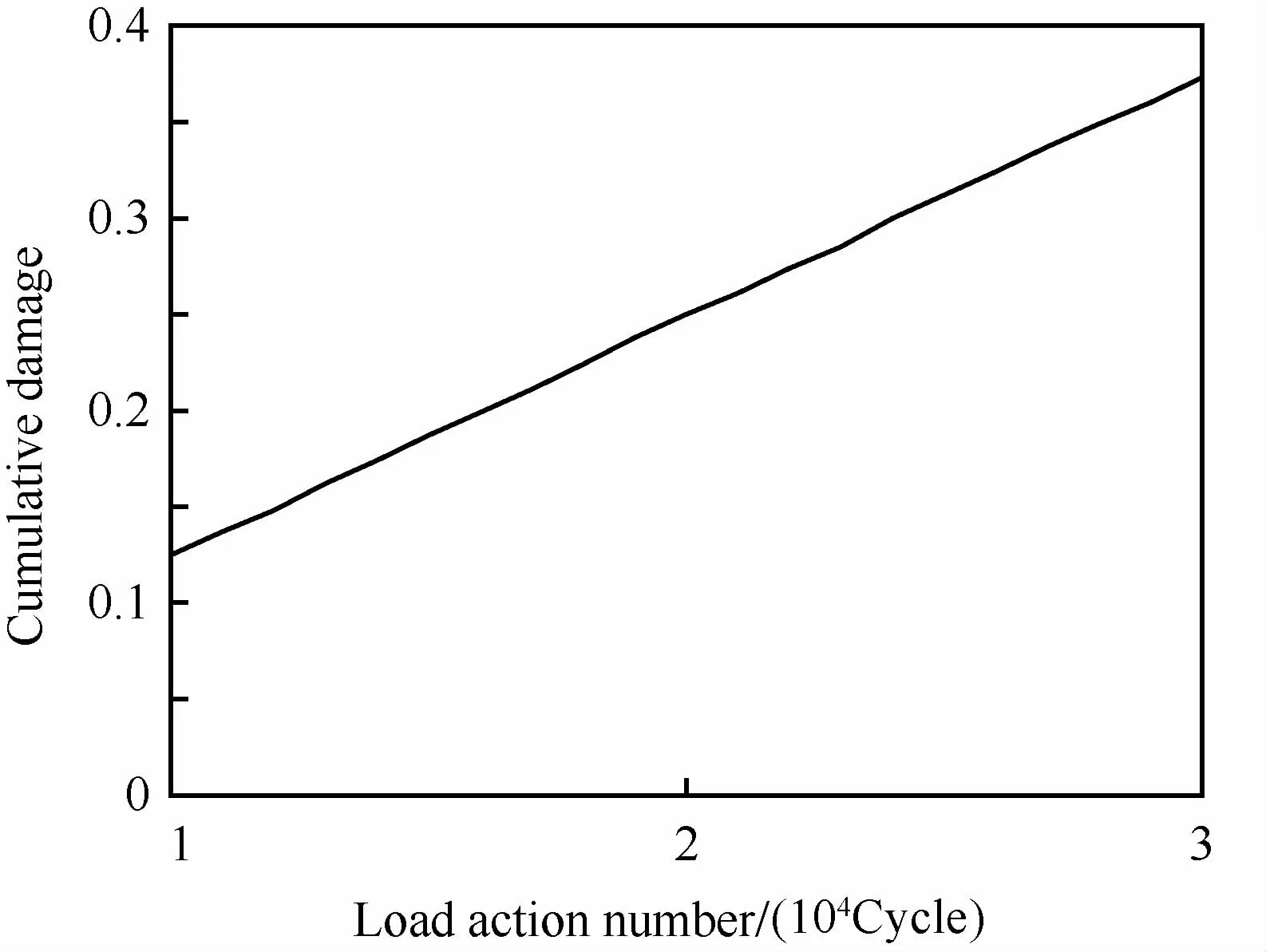
图6 累积损伤与载荷循环数之间的关系Fig.6 Relationship between cumulative damage and load action number

继而,根据本文推导出的一个损伤部位的失效概率计算式(15)及多部位损伤零部件的失效概率计算式(17),可以得到失效概率与载荷循环次数之间的关系,如图7所示。

由计算结果可知,在给定失效概率时,含有多个损伤部位的复杂零部件的寿命会比只有一个损伤部位时的寿命低很多,这是由寿命的不确定性效应导致的。显然,寿命的随机性越大,多损伤部位复杂零部件的寿命与只有一个损伤部位时的寿命差别也越大。

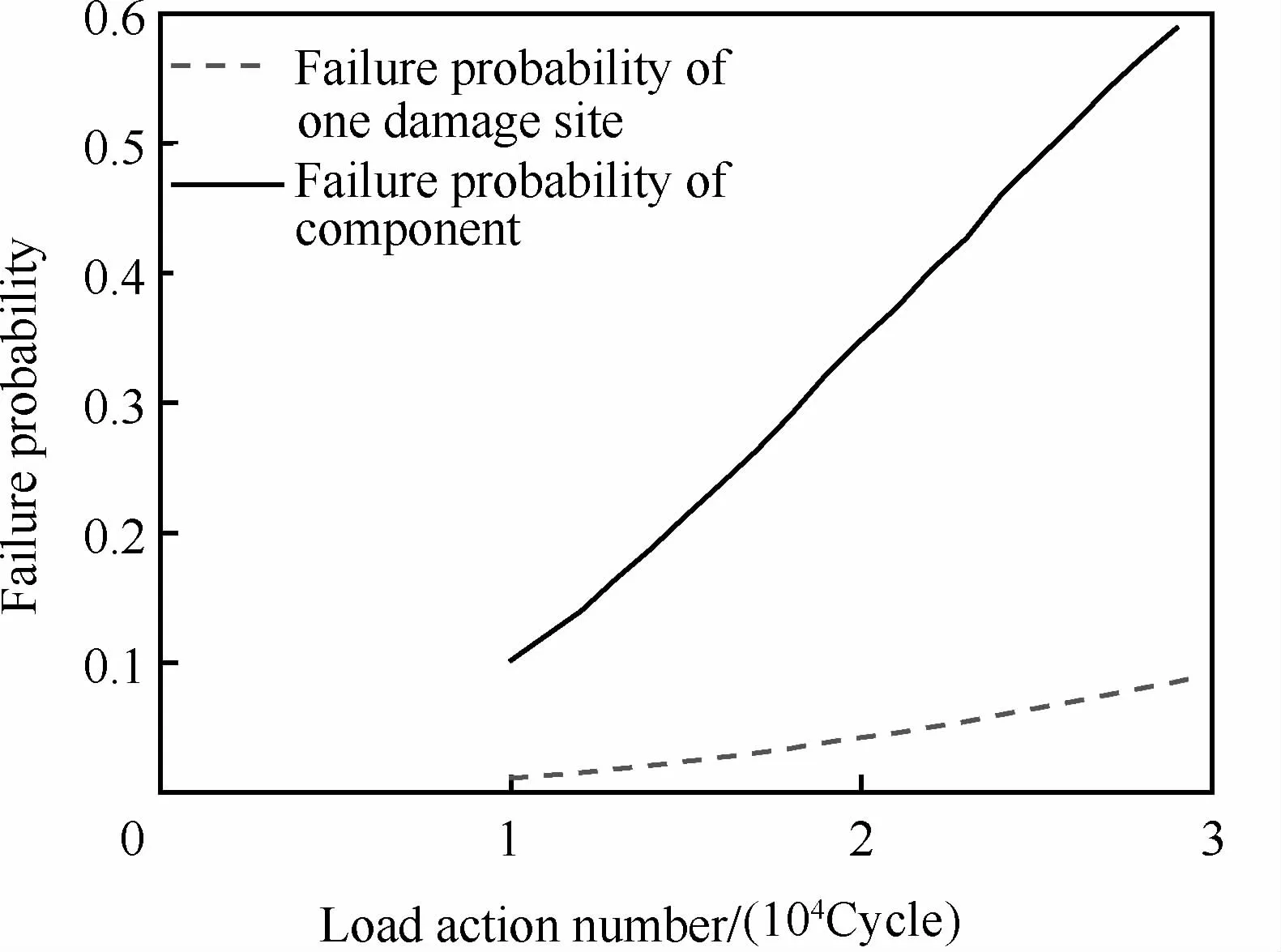
图7 失效概率与载荷循环次数之间的关系Fig.7 Relationship between failure probability and load action number

5 结 论

提出了一种基于寿命中值计算疲劳累积损伤的概率损伤法则(中值累积损伤法则)以及确定损伤临界值概率分布的方法。以中值累积损伤法则为基础,应用多层统计分析及全概率原理,提出了多部位损伤结构和复杂零部件的概率寿命预测方法及模型。中值累积损伤法则体现了疲劳损伤等效与疲劳失效概率等效的一致性。提出的概率寿命预测方法应用方便,需要的材料性能数据只有中值S-N曲线和某一应力水平下的寿命分布,且能反映载荷历程的随机性对寿命及可靠性的影响。算例显示,多损伤结构零部件的概率疲劳寿命与只有一个损伤部位时的概率疲劳寿命有明显差别。如果只根据零部件上多个较高应力部位中的一个最高应力部位预测其疲劳寿命,会导致偏于危险的结果。

[1] Silva L F M,Goncalves J P M,Oliveira F M F,et al.Multiple-site damage in riveted lat-joints:Experimental simulation and finite element prediction[J].International Journal of Fatigue,2000,22(4):319-338.

[2] Mkaddem A,Mansori M E.An equivalent ellipse method to analyze the fatigue behavior following‘multi-surface initiations’[J].International Journal of Mechanical Sciences,2010,52(9):1125-1135.

[3] Jones R,Molent L,Pitt S.Study of multi-site damage of fuselage lap joints[J].Theoretical and Applied Fracture Mechanics,1999,32(2):81-100.

[4] Park J H,Singh R,Pyo C R,et al.Integrity of aircraft structural elements with multi-site fatigue damage[J].Engineering Fracture Mechanics,1995,51(3):361-380.

[5] Lee H,Kim N.Fatigue life prediction of multi-spot-welded panel structures using an equivalent stress intensity factor[J].International Journal of Fatigue,2004,26(4):403-412.

[6] Salvini P,Vivio F,Vullo V.Fatigue life evaluation for multi-spot welded structures[J].International Journal of Fatigue,2009,31(1):122-129.

[7] Wang X,Modarres M,Hoffman P.Analysis of crack interactions at adjacent holes and onset of multi-site fatigue damage in aging airframes[J].International Journal of Fracture,2009,156(2):155-163.

[8] Park J H,Atluri S N.Fatigue growth of multiple-cracks near a row of fastener-holes in a fuselage lap-joint[J].Computational Mechanics,1993,13(3):189-203.

[9] O’Donoghue P E,Atluri S N,Pipkins D S.Computational strategies for fatigue crack growth in three dimensions with application to aircraft components[J].Engineering Fracture Mechanics,1995,52(1):51-64.

[10] Markiewicz I.Analysis of hole arrangement in tensile plate by means of the SADSF method and fatigue life predictions[J].Maintenance and Reliability,2009,43(3):24-31.

[11] Zhao J M,Chan A H C,Roberts C,et al.Reliability evaluation and optimization of imperfect inspections for a component with multi-defects[J].Reliability Engineering and System Safety,2007,92(1):65-73.

[12] Proppe C.Probabilistic analysis of multi-site damage in aircraft fuselages[J].Computational Mechanics,2003,30(4):323-329.

[13] Lambert S,Pagnacco E,Khalij L.A probabilistic model for the fatigue reliability of structures under random loadings with phase shift effects[J].International Journal of Fatigue,2010,32(2):463-474.

[14] Ni K,Mahadevan S.Strain-based probabilistic fatigue life prediction of spot-welded joints[J].International Journal of Fatigue,2004,26(7):763-772.

[15] Murty A S R,Gupta U C,Krishna A R.A new approach to fatigue strength distribution for fatigue reliability evaluation[J].International Journal of Fatigue,1995,17(2):85-89.

[16] Zhang D,Hong J,Ma Y,et al.A probability method for prediction on high cycle fatigue of blades caused by aerodynamic loads[J].Advances in Engineering Software,2011,42(12):1059-1073.

[17] Petryna Y S,Pfanner D,Stangenberg F,et al.Reliability of reinforced concrete structures under fatigue[J].Reliability Engineering and System Safety,2002,77(3):253-261.

[18] Karadeniz H.Uncertainty modeling in the fatigue reliability calculation of offshore structures[J].Reliability Engineering and System Safety,2002,74(3):323-335.

[19] Kliman V.Fatigue life estimation under random loading using the energy criterion[J].International Journal of Fatigue,1985,7(1):39-44.

[20] Xie L Y,Zhou J Y,Wang Y Y,et al.Load-strength order statistics interference models for system reliability evaluation[J].International Journal of Performability Engineering,2005,1(1):23-36.