机翼后缘柔性支撑结构的拓扑优化

金栋平*,纪斌

南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016

变形机翼可根据不同的飞行条件自适应地改变自身构形来提高飞行器的气动性能[1-2],其中改变机翼弯度是一种重要方式,而机翼前/后缘偏转是改变弯度的一种重要形式[3-5]。传统变弯度机翼通过偏转前/后缘襟翼等方法改变翼型弯度,使得机翼在襟翼偏转处形成缝隙和折线,破坏了翼面的光滑性和连续性,导致气流提早分离,造成阻力增加、燃油利用率降低。与传统的前/后缘襟翼及常规偏折控制面相比,采用柔性结构可以光滑而持续地改变机翼形状,能使气动性能明显提高[6-7]。

柔性结构可根据工作条件,利用自身的弹性变形实现一定轮廓形状的改变。密歇根大学的Kota教授等[8-9]提出用柔性结构实现机翼前/后缘可变的设计思路,并利用柔性结构研制出可实现0°～6°变化的机翼前缘,使升力系数提高25%,升阻比提高51%。Podugu和Ananthasuresh[10]使用形状对比法对机翼前/后缘进行拓扑优化,并将形状记忆合金用于优化后的结构。国内开展柔性变形机翼研究的主要有西北工业大学的葛文杰团队[11],他们分别从离散体和连续体两个方面对柔性机翼进行拓扑优化分析,并进行了理论论证和变形试验。陈秀等[12]以实际变形曲线与目标曲线之差最小作为优化目标,采用遗传算法对柔性结构的尺寸、形状、拓扑进行了综合优化。黄杰[13]和 Tong[14]等基于SIMP(Solid Isotropic Micro-structure with Penalization)方法密度-刚度插值模型,实现了用于机翼前缘形状连续变化的柔性结构拓扑优化。

拓扑优化发展至今,涌现出多种优化方法。Bendsøe[15]提出了SIMP方法,并得到了广泛认可。Sigmund[16-17]在SIMP基础上,对灵敏度进行了改进以有效解决结构最小柔度问题。Sethian和Wiegmann[18]则将水平集法引入到结构拓扑优化中。遗传算法作为一种广义的优化方法被广泛用于结构拓扑优化。Jakiela[19]和Wang[20-21]等提出位矩阵编码的遗传算法,利用位矩阵将设计域离散,用于解决连续结构的拓扑优化问题。上述方法对于单目标拓扑优化问题,通过施加约束可得到满意优化结果。对于多目标优化问题,Deb等[22]提出的非支配排序遗传算法(Nondominated Sorting Genetic AlgorithmⅡ,NSGA-Ⅱ)是一种被广泛采用的多目标优化算法,可以快速搜寻到Pareto前沿优解。

通常,机翼后缘受到的气动力相对较小,面外承载能力要求相对前缘要低。机翼后缘变形可有效提高气动性能,将柔性结构用于机翼后缘具有重要作用。本文针对满足不同要求的机翼后缘柔性支撑结构,考虑面外承载、变形性能等多个优化目标,使用位矩阵对机翼后缘曲面进行编码,并利用NSGA-Ⅱ对该优化问题进行研究。通过对违约个体进行惩罚,实现基于位矩阵的NSGA-Ⅱ多目标算法,以得到用于机翼后缘优化的可行、有效的柔性支撑结构。

1 优化对象及目标函数

1.1 优化对象

在外力作用下,机翼后缘柔性结构产生变形,引起机翼弯度的改变,如图1所示。

图1 机翼后缘柔性结构Fig.1 Flexible wing at trailing edge

选取机翼后缘曲面的一段作为优化对象,长度为机翼弦长Lc的1/4,如图2所示。位矩阵x表示离散后的机翼后缘曲面,若单元充满材料,则位矩阵x中相应元素为1；若单元为空,则位矩阵x中相应元素为0。

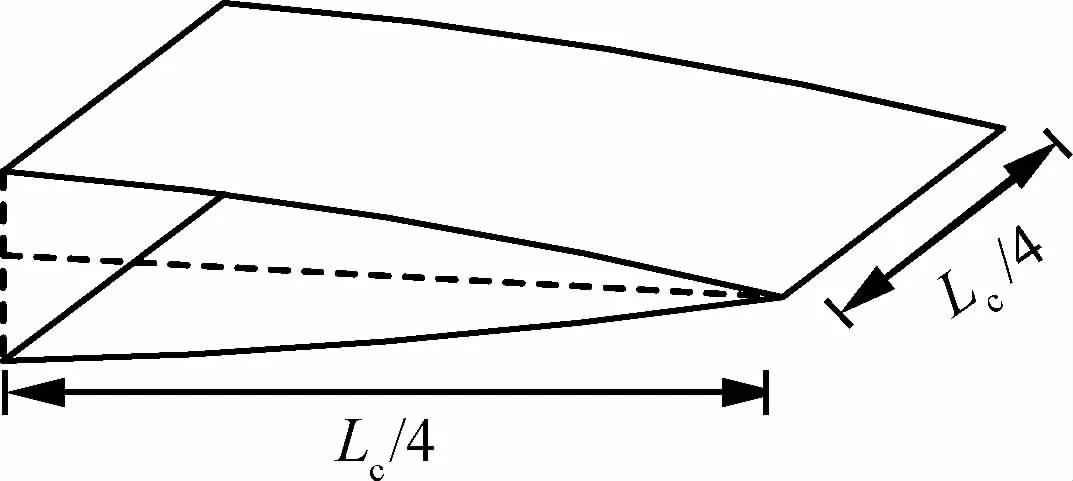
图2 机翼后缘曲面Fig.2 Surface of trailing edge

1.2 优化目标

1)对于飞行器,自重是需要考虑的一个重要方面,选取质量较轻的结构,可以减少飞行过程中的能量消耗。对于由单一材料构成的结构,将柔性支撑结构的体积V(x)作为优化目标。

2)在气动载荷p的作用下,柔性支撑结构应具有维持机翼外形的能力。图3为柔性支撑结构的气动载荷及其边界约束示意图,结构左端边界简支,限制x、y、z方向的位移。结构局部z向位移δz(x,p)越小,维持机翼外形的能力越强。

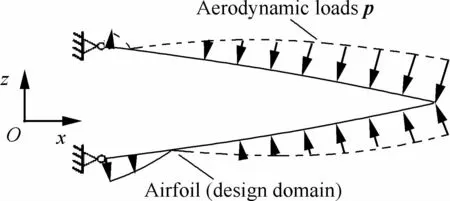
图3 柔性支撑结构的气动载荷及其边界约束Fig.3 Aerodynamic loads and boundary conditions of flexible support structure

3)为使机翼后缘易于变形,柔性支撑结构变形所需能量应尽量小。图4为柔性支撑结构变形及其边界约束示意图,结构左端边界简支,限制x、y、z方向位移,结构右边界简支,限制x、y方向位移,结构右端可沿z方向运动。结构右端给定z方向位移uz,柔性支撑结构总应变能Wmorph越小,结构越易变形。

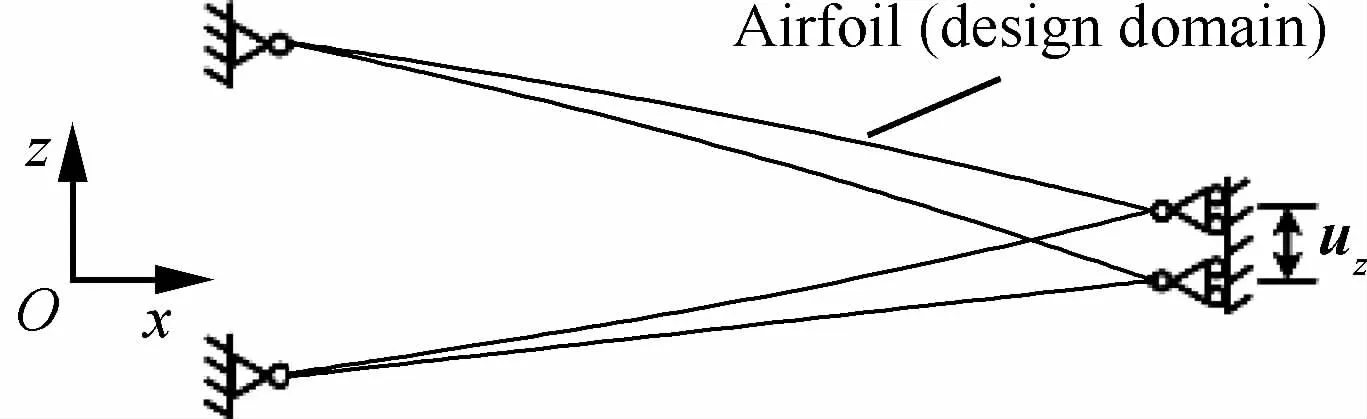
图4 柔性支撑结构变形及其边界约束Fig.4 Bending deflection and boundary conditions of flexible support structure

综上所述,柔性支撑结构的优化问题具有3个优化目标,可以表示为

2 拓扑优化算法实现

2.1 基因表示方式

二维连续结构拓扑优化问题,可使用位矩阵来表示离散后的设计域,其相对二进制编码和实数编码更直观,同时避免了遗传算法中的编码和解码环节。设定离散后的单元只存在两种状态:充满材料或者为空。如图5所示,将拓扑结构表示为0-1矩阵。

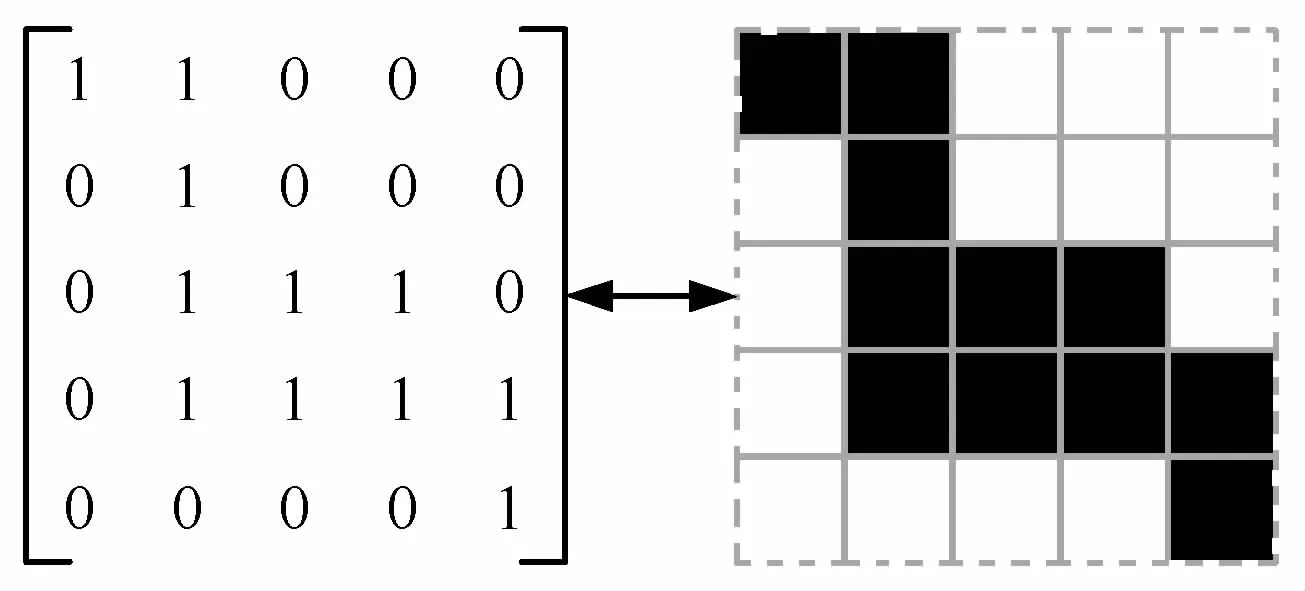
图5 设计域的位矩阵基因Fig.5 Bit-matrix representation of design domain

2.2 交叉与变异算子

在遗传算法中,交叉与变异算子用于产生新的个体,从而增加搜索范围。交叉算子通过交换父代的基因来获得新的个体,是主要的遗传算子。传统的实数或二进制交叉在处理二维基因时会产生垂直方向几何偏见,为避免此情况,这里采用二维交叉算子。

变异算子作为遗传算法的辅助算子,在设计空间实施随机漫步,增加种群的多样性和搜索的全局性。本文采用矩阵的异或运算作为变异算子,随机产生一个与个体位矩阵尺寸相同的位矩阵,其元素1随机分布且所占比例为预设的变异范围值Pm,变异算子如图6所示,图中xor表示异或运算。

图6 变异算子Fig.6 Mutation operator

2.3 个体连通性分析

在个体中,若一组材料块中的每个材料块都与其周围的材料块至少共有一条边,则认为这组材料块为一个连续体。若连续体满足边界条件和载荷条件,则该个体含有传力路径。若连续体不满足边界条件或载荷条件,该连续体为无用连续体。如图7所示,柔性支撑结构离散为20×40个单元,虚线左右分别为上下翼面。图7中有3个连续体,连续体1为一条传力路径,连续体2、3为无用连续体。

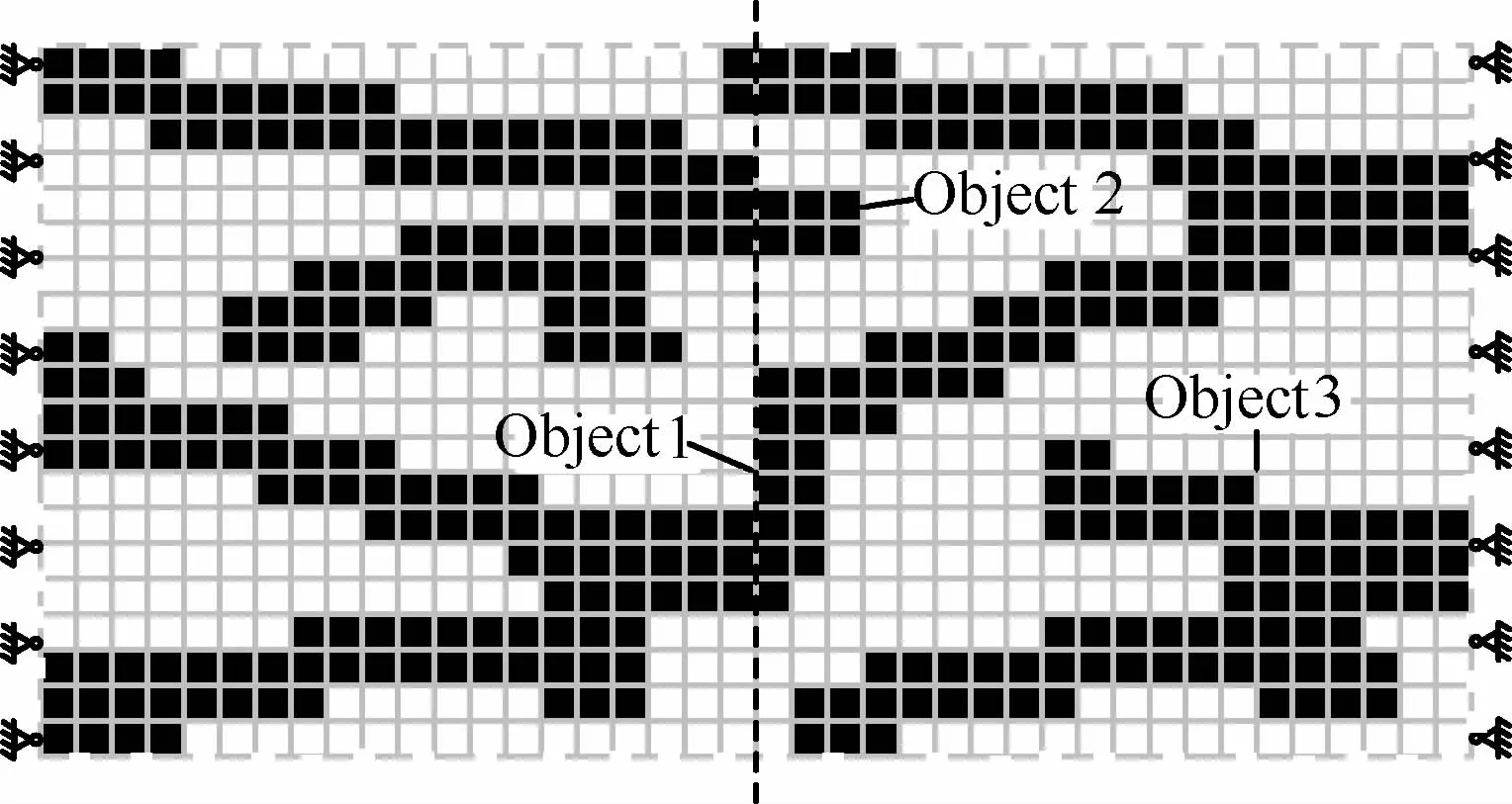
图7 个体连通性分析Fig.7 Connectivity analysis of individual

希望通过拓扑优化得到的结构只存在一条传力路径,将个体中传力路径个数作为约束条件,柔性支撑结构的拓扑优化问题可表示为

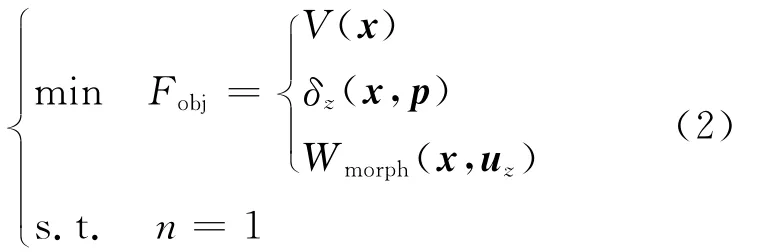
式中:n为个体中传力路径的条数。

根据个体违约程度,对个体施加不同的惩罚值,使个体向满足约束条件的方向进化。参考Wang和Tai[21]提出的惩罚方法,个体惩罚值为

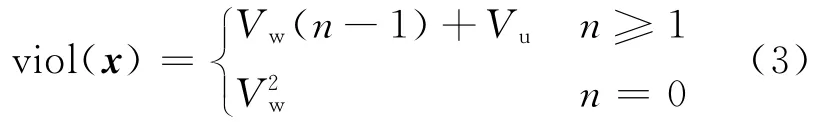
式中:Vw为整个设计域的体积；Vu为无用连续体的总体积。

2.4 相似个体过滤

为保持种群个体的多样性,扩大遗传算法的搜索范围,对于种群中的相似个体进行过滤。使用Jaccard相似系数来描述个体间的相似度,Jaccard相似系数定义为

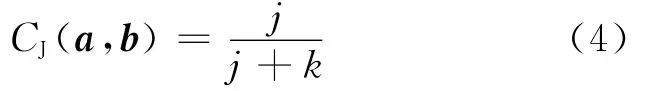
式中:a和b为种群中两个个体的位矩阵；j为两个位矩阵对应元素都为1的元素个数；k为对应元素只有一个为1的元素个数。CJ(a,b)反映了a、b矩阵的相似程度,值在[0,1]范围之内,两个个体完全相同时,CJ(a,b)=1。通过限定CJ的取值,对种群中的个体进行分类,每一类只保留最优的个体。

2.5 种群初始化

对于拓扑优化问题,通常是令初始种群中的一半个体布满材料,一半个体完全没有材料。本文将随机产生与连通性分析相结合。给定每个个体体积与设计域总体积之比Pd,Pd(i)表示为

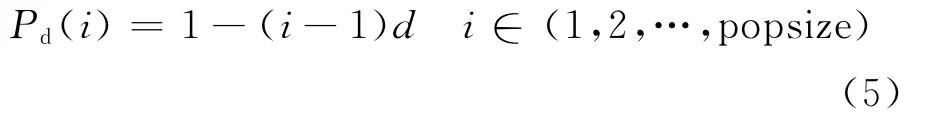
式中:i为个体编号；d为相邻个体体积比之差；popsize为种群规模。随机产生体积比为Pd(i)的个体,直到其满足连通性条件,重复此过程来构造初始种群。

2.6 拓扑优化算法流程

将初始种群大小设为20,个体离散为20×40个单元。选择算子采用二元锦标和精英策略。由于采用了精英策略,为了加快搜索速度,将交叉概率和变异概率设为100%。在算法初始阶段,变异范围值Pm应大些,进行大范围搜索,随着代数的增加,减小变异范围,进行局部搜索。类似高斯变异,变异范围设定为

式中:curGen为当前代数；max Gen为预设最大代数,本研究将max Gen设定为105。图8为整个拓扑优化算法的流程,Pt和Ct分别为父代和子代种群,Rt为父代与子代合并后的种群。

图8 基于非支配排序遗传算法(NSGA-Ⅱ)拓扑优化算法流程Fig.8 Process of topology optimization based on non-dominated sorting genetic algorithmⅡ (NSGA-Ⅱ)

3 计算结果与讨论

算例采用翼型NACA0012,翼型弦长为1 m,厚度为0.001 m,弹性模量为1 GPa,泊松比为0.3。施加Ma=0.8、攻角1.25°的气动载荷。通过迭代得到20个满足要求的构形,将构形按体积V(质量)从小到大排列,如图9所示。图中每个解左侧为机翼后缘上表面,右侧为下表面。可以看出,20种构形形态各异,表明基于NSGA-Ⅱ的多目标拓扑优化算法具有较强的全局搜索能力,可以有效地寻找到符合要求的构形。

图9 拓扑优化解Fig.9 Solutions of topology optimization

图10 为20种构形在目标空间的分布情况,整体来看,图10(a)表明δz(承载能力)与Wmorph(变形能力)相冲突；图10(b)表明V(质量)较大的结构往往可以更好地保持机翼外形；图10(c)表明Wmorph(变形能力)与V(质量)近似呈反比例关系。

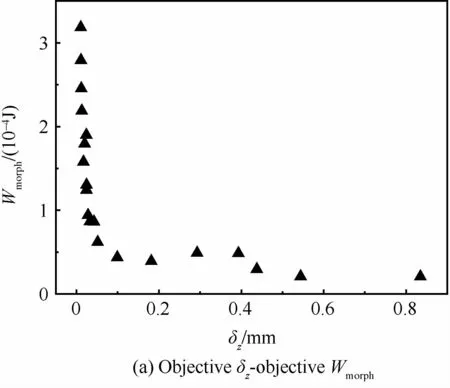
图10 个体在目标空间的分布Fig.10 Distribution of solutions in objective space

图11 给出了归一化的目标值¯V、¯δz和¯Wmorph。可以看出,解1具有最小质量,解20保持机翼外形的能力最强,解7具有最好的弯曲变形能力。

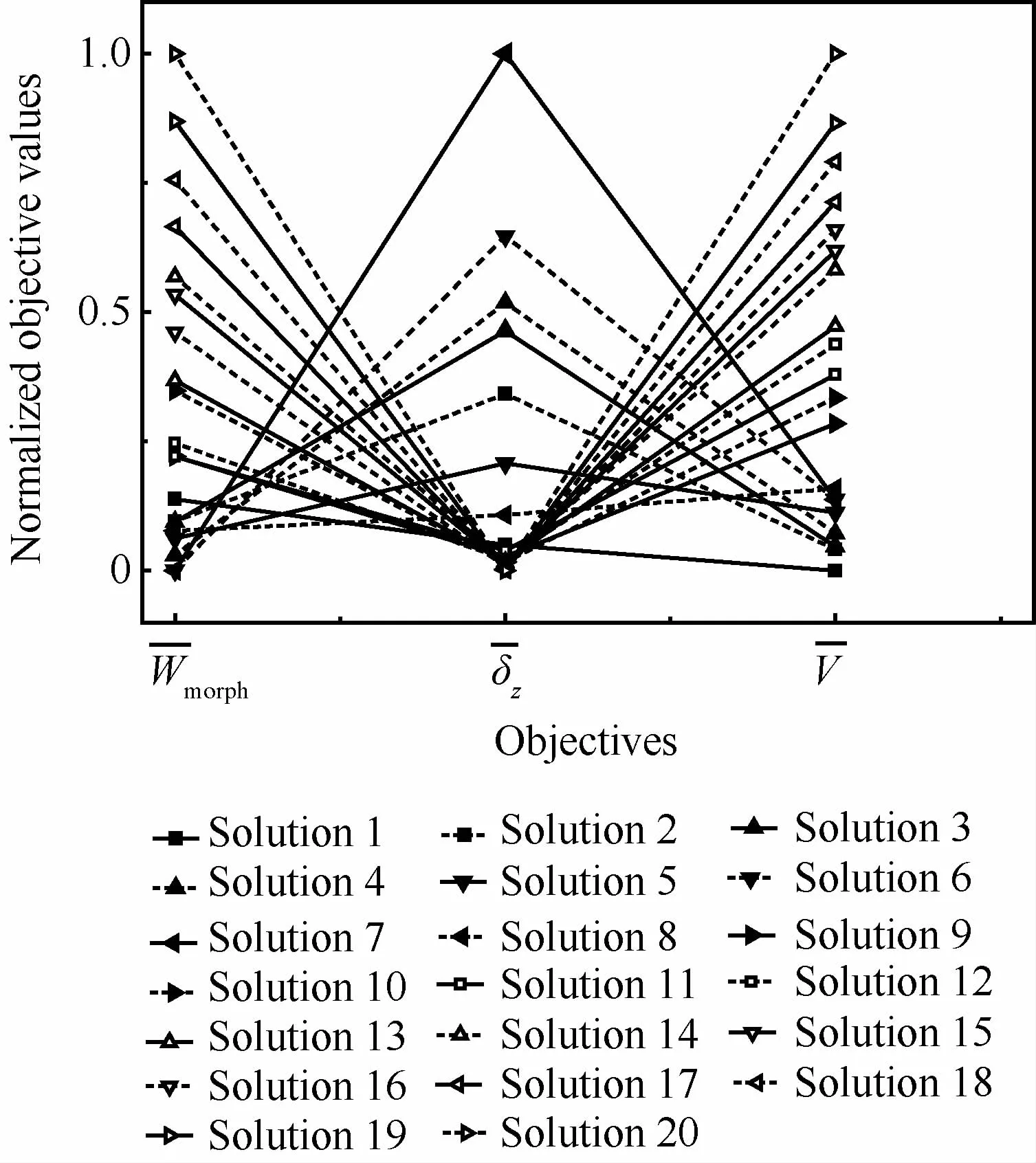
图11 归一化的目标值Fig.11 Normalized objective values

由于多目标优化问题的特点,各个目标之间相互制约,难以明确指出这20个解中哪个是最优解。在实际应用中,可以根据不同的需求来选择相应的构形。

4 结 论

1)使用位矩阵表示离散后的设计域,相对于二进制编码和实数编码更直观,同时避免了遗传算法中编码和解码环节,无需考虑个体可能出现的上、下限溢出的情况。

2)通过引入连通性分析和相似个体滤波,避免了对非可行个体不必要的计算,增加了种群的多样性,扩大了算法的搜索范围。

3)采用基于NSGA-Ⅱ的拓扑优化算法,可对用于机翼后缘的柔性结构进行多目标拓扑优化。相比于单目标优化只有一种优化构形,该方法可以得到多种拓扑构形。每种构形都具有其优势和劣势,在实际应用中,可根据不同需求选择合适的构形。

[1] Barbarino S,Bilgen O,Ajaj R M,et al.A review of morphing aircraft[J].Journal of Intelligent Material Systems and Structures,2011,22(9):823-877.

[2] Sofla A Y N,Meguid S A,Tan K T,et al.Shape morphing of aircraft wing:status and challenges[J].Materials Design,2010,31(3):1284-1292.

[3] Joshi S P,Tidwell Z,Crossley W A,et al.Comparison of morphing wing strategies based upon aircraft performance impacts[C]//Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2004:1722-1729.

[4] Ahmed S,Guo S.Optimal design and analysis of a wing with morphing high lift devices[C]//Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Reston:AIAA,2013:1880-1895.

[5] Vasista S,Tong L,Wong K C.Realization of morphing wings:a multidisciplinary challenge[J].Journal of Aircraft,2012,49(1):11-28.

[6] Midha A,Norton T W,Howell L L.On the nomenclature,classification,and abstractions of compliant mechanisms[J].Journal of Mechanical Design,1994,116(1):270-279.

[7] De Gaspari A,Ricci S.A two-level approach for the optimal design of morphing wings based on compliant structures[J].Journal of Intelligent Material Systems and Structures,2011,22(10):1091-1111.

[8] Saggere L,Kota S.Static shape control of smart structures using compliant mechanisms[J].AIAA Journal,1999,37(5):572-578.

[9] Kota S,Hetrick J A,Osborn R,et al.Design and application of compliant mechanisms for morphing aircraft structures[C]//Smart Structures and Materials:Industrial and Commercial Applications of Smart Structures Technologies.San Diego:Society of Photo-Optical Instrumentation Engineers,2003:24-33.

[10] Podugu P,Ananthasuresh G K.Topology optimizationbased design of a compliant aircraft wing for morphing leading and trailing edges[C]//Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition.Vancouver:American Society of Mechanical Engineer,2010:1099-1107.

[11] Liu S L,Ge W J,Li SJ.Optimal design of compliant trailing edge for shape changing[J].Chinese Journal of Aeronautics,2008,21(2):187-192.

[12] Chen X,Ge W J,Zhang Y H.Investigation on synthesis optimization for shape morphing compliant mechanisms using GA[J].Acta Aeronautica et Astronautica Sinica,2007,28(5):1230-1235(in Chinese).陈秀,葛文杰,张永红.基于遗传算法的柔性机构形状变化综合优化研究[J].航空学报,2007,28(5):1230-1235.

[13] Huang J,Ge W J,Yang F.Topology optimization of the compliant mechanism for shape change of airfoil leading edge[J].Acta Aeronautica et Astronautica Sinica,2007,28(4):988-992(in Chinese).黄杰,葛文杰,杨方.实现机翼前缘形状连续变化柔性机构拓扑优化[J].航空学报,2007,28(4):988-992.

[14] Tong X,Ge W,Sun C,et al.Topology optimization of compliant adaptive wing leading edge with composite materials[J].Chinese Journal of Aeronautics,2014,27(6):1488-1494.

[15] Bendsøe M P.Optimal shape design as a material distribution problem[J].Structural Optimization,1989,4(1):193-202.

[16] Sigmund O.A 99 line topology optimization code written in MATLAB[J].Structural and Multidisciplinary Optimization,2001,21(2):120-127.

[17] Sigmund O.Morphology-based black and white filters for topology optimization[J].Structural and Multidisciplinary Optimization,2007,33(4-5):401-424.

[18] Sethian J A,Wiegmann A.Structural boundary design via level set and immersed interface methods[J].Journal of Computational Physics,2000,163(2):489-528.

[19] Jakiela M J,Chapman C,Duda J,et al.Continuum struc-tural topology design with genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering,2000,186(2):339-356.

[20] Wang S Y,Tai K.Structural topology design optimization using genetic algorithms with a bit-array representation[J].Computer Methods in Applied Mechanics and Engineering,2005,194(36):3749-3770.

[21] Wang S Y,Tai K.Graph representation for structural topology optimization using genetic algorithms[J].Computers&Structures,2004,82(20):1609-1622.

[22] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.