高性能飞机发展对控制理论的挑战

史忠科*

西北工业大学 自动化学院,西安 710072

目前,国内外很多研究工作者以飞行器作为控制方法的研究背景,很多实验室都购买了稳定性很好的四旋翼无人机以探讨飞行控制问题。同时,飞行控制的仿真研究也方兴未艾。然而,飞行安全是现代飞行控制面临的主要问题。现代战斗机为满足全包线超机动能力和高机敏性要求放宽了静稳定性,相应的不稳定和过失速机动使得飞行安全问题十分凸显；大型军用运输机在超低空重载空投过程中出现性能突变容易造成机毁人亡；民用飞机的短距起降和舰载机起飞/着舰过程中的多种因素使得飞行事故屡屡发生,固定翼或单旋翼战术无人机试验中也常常发生飞行事故。为此,本文对飞行器控制问题进行了简要综述,以便为飞行控制研究工作提供参考。

1 飞机大迎角机动对非线性控制理论的挑战

飞机大迎角飞行是现代和未来高性能飞机的重要标志。飞机在进行过失速机动时,利用大迎角下自身所受到的很大阻力,飞行员可灵活操纵飞机绕速度轴滚转,使机头快速指向任意方向,既可以获得指向优势对敌实施打击,也可以规避敌方攻击并很快转入反击,提高自身的生存能力。因此,过失速机动能力是取得空战优势的关键因素之一,也是现代和未来先进战斗机的主要特征之一。然而,飞机大迎角机动会跨越飞行安全包线,进入尾旋/偏离状态甚至导致机毁人亡。因此,对飞机大迎角特性的系统分析和控制研究,对于飞机大迎角飞行时操纵控制系统既能极大发挥战术性能,又可以确保飞行安全等有着极为重要的实际意义。

现代和未来高性能战斗机研究依赖于大迎角特性。在目前与将来相当长的时间内,战斗机空战仍会存在近距格斗的模式。现代战斗机通过气动布局的优化所达到的最大升力系数和失速迎角已基本达到极限,很难再使飞机的常规机动性相对于其他战斗机有明显的优势,而且战斗机进行常规机动在一定范围内还要受到人体承受过载能力的限制；虽然新型近距格斗导弹具备大离轴角发射甚至越肩攻击的能力,但在发射初期推力矢量的使用会极大地消耗火箭能量,造成导弹的射程明显减小。由此可知,机头的快速精准指向目标,仍是提高飞机格斗能力的重要手段之一。过失速机动极大地提高了机头指向目标的速度,大大增加了战斗机在格斗中的攻击机会,目前和未来战机的过失速机动常常需要强迫飞机进入大迎角区域。第四代战斗机(俄罗斯称五代机)已经具有很完善的过失速机动能力,经验很丰富的飞行员可以完成“尾冲”、“眼镜蛇”和“锥子”等比较简单的过失速机动,也可以完成在水平盘旋中进入过失速,然后绕速度矢量滚转成直立的稳态大迎角飞行的“猫鼬”动作和难度很高的“赫伯斯特”机动。然而,飞机进入失速等大迎角飞行状态的危险性极大,如果不能有效操控,就可能机毁人亡。如何正确利用飞机大迎角特性已经成为现代和未来战斗机研究的重点内容。

飞行控制方法直接影响大迎角特性的发挥。飞机大迎角流动通常是指气流发生分离,空气动力呈现非线性特性的飞行区域。新一代战机普遍采用小展弦比、尖前缘的机翼、利用翼前缘涡的分离产生的非线性增长的升力,增大飞机的升阻比以提高飞机的失速迎角。但是当迎角过大时,涡在运动过程中受逆压梯度或粘性损耗的影响会发生涡核破裂,使得涡核处的轴向速度会突降、周径突然扩大且压力增加,导致环流逐渐取代原有涡的集中涡核,发生在机翼上方的涡破裂会对机翼的气动特性产生极为不利的影响。由于机翼、机身随迎角和马赫数的增大会出现各种复杂流态,机翼涡和机头涡的形成、形态和发展过程、涡的空间轨迹和涡的破裂位置以及涡系之间的相互干扰都将对飞机的气动特性产生很大影响,引起气动力和力矩的高度非线性和非定常迟滞特性,这就使大迎角下的气动特性以及由此产生的过失速等特殊机动现象和飞机操纵十分复杂,很难由试飞员给出合理的评价和操纵规则,而必须通过复杂系统分析并设计控制器使得飞机发挥优良的大迎角特性。因此,飞行控制方法成为当今的研究主题。

飞机大迎角建模与控制是中国未来战斗机研制和保证飞行安全的瓶颈,需要加速研究。随着第4代战斗机设计中推力矢量和先进气动力控制等大迎角控制技术的实际应用带来的飞行包线大幅扩展,以及雷达系统、飞行控制系统和武器导弹系统的不断改进与更新,战机的生存环境急剧恶化,飞机的大迎角机动飞行能力己经成为战机攻击与防卫的必要手段。中国在当今和未来战斗机的设计中将更加重视大迎角机动性能,而国内研究工作积累少,可供研究使用的风洞和飞行试验数据少,使得飞机大迎角建模与控制成为未来战斗机研制和保证飞行安全的瓶颈,失速和过失速迎角范围内战机模型的动态特性及控制特性研究已经刻不容缓,必须在几年时间内给出能够指导实际的有关理论方法和研究结果,才能为新一代和未来高性能战机的研发提供有力的技术支持和安全保障,促进新一代和未来战机的研制速度,使中国新型战机在生存环境日益恶化的未来空战中处于强势地位。

飞机在大迎角飞行时,由于机身周围流场的空气动力学特性极为复杂,一个小的姿态变化,就可能导致较大的气动力和气动力矩变化,从而导致操纵性和稳定性的急剧变化,出现强惯性耦合、机翼摇晃、深失速和尾旋等诸多危险的非线性运动现象,严重威胁着战机的机动安全和作战效能。国内外关于大迎角气动特性研究主要有风洞试验方法、流体力学理论分析、通过参数辨识飞行试验或风洞试验的数据建立大迎角气动力数学模型分析3种方法,并针对惯性耦合、机翼摇晃、过失速机动和尾旋等非线性现象开展了一定的研究工作。

1)惯性耦合研究

惯性耦合是指飞机作快速横滚机动飞行时,由于本身质量的惯性力矩而使迎角和侧滑角大幅度变化的现象,又称惯性交感。现代高性能战斗机,滚转通道一般都设计成绕速度矢量滚转,滚转轴不在飞机的惯性主轴上,因此,惯性耦合问题是不可避免的。国内外诸多学者对惯性耦合问题进行了大量的研究。Phillips[1]很早就对定常滚转耦合进行了研究,得出了对工程设计有重要参考价值的Phillips稳定性判据；Mehra等[2]用分叉突变理论方法对机动飞机的五阶运动方程进行了分叉分析,计算了滚转耦合过程中的分叉面,对滚转过程中的跳跃现象和极限环运动进行了深入的探讨；Liefer[3]研究了惯性耦合对现代战斗机敏捷性的影响；Jahnke[4]采用8阶方程对惯性耦合进行了研究,计算了滚转过程中惯性耦合力矩和分叉面；Goman等[5]对非线性飞行动力学中的非线性现象进行了系统的综述,对诸多学者的工作进行了总结,对滚转耦合问题进行了详细的讨论；Modi和Ananthkrishnan[6]采用拟定常方法对绕速度矢量的快速滚转进行了研究,给出了由于惯性耦合引起的跳跃现象的抑制措施。

2)机翼摇晃研究

机翼摇晃是一种非指令的横滚偏航振荡,以大幅度滚转振荡为主,较小程度偏航振荡为辅,还伴有高频率的轻微俯仰振荡。它是一种中高迎角下特有的复杂非线性空气动力学现象,与翼面上涡的不对称发展和涡的破裂特性密切相关。在试验方面,此类机理性探索试验大多数是针对单个机翼在低速风洞中进行的,且局限于滚转单自由度。关于机翼摇晃的诱因,比较一致的观点是机翼摇晃是由翼面涡的不对称性发展引发并维持；较大迎角下涡的破裂对此极限环振荡又起限幅和降幅作用,为了适应新型战机的设计需要,近年来,翼-体摇晃、非细长翼摇晃及跨音速下机翼摇晃也逐渐纳入航空界的研究范畴,并引起了欧美各军事强国的足够重视。机翼摇晃的理论研究主要涉及振荡模型的构建、模型的理论分析以及模型的振荡抑制等。单自由度模型研究开展较早,再加上相对简单,因此研究比较透彻和深入。单自由度模型虽然易于分析,但适用迎角范围较小；且无法探究俯仰、偏航两自由度对滚转振荡造成的影响；另外试验数据来源决定了其只能用于近似分析低音速的机翼摇晃现象,与实际飞行相差甚远。近年来的二自由度、三自由度模型都不可避免地进行了一些利于建模和分析的假设。文献[7-22]等利用欧拉角变换推导二自由度机翼摇晃模型时就假定忽略偏航振荡；Go和Ramnath[23]利用Lagrange方程建立的三自由度先进战斗机机翼摇晃模型的频率和幅值都很小,从而导致仿真时各振荡方向的幅值都很小；采用多自由度机翼摇晃模型在实用性及仿真精度上明显优于低自由度模型,但计算分析却较为复杂,动态气动力和力矩的计算需要充分的实际飞行和风洞试验数据；目前研究机翼摇晃大多数基于Ross模型[23-29]。机翼摇晃模型的分析与控制在近年来一直为人们所重视,研究内容涉及极限环振荡的幅值、频率和起始迎角的近似估算、预测指标的假设和验证、模型的稳定性分析以及机翼振荡的抑制等。低自由度模型的理论分析开展较早且相对比较深入,常用分析方法有摄动理论、相平面图法、分叉突变理论、小扰动线性化、多时间尺度法及中心流形降维法。多维高阶非线性模型的分析难度很大,或需要降阶,或通过分叉突变理论、平衡点附近小扰动线性化分析等。多数机翼摇晃的控制研究也是针对单自由度机翼摇晃模型,涉及的控制算法包括模糊控制、最优控制、神经网络控制、自适应控制、反步控制、非线性动态逆、庞特里亚金最大值法 (Pontryagin Maximum Principle,PMP)和李雅普诺夫函数法(Lyapunov Function Method,LFM)；而对于高维机翼摇晃模型,目前多数控制分析基于平衡点附近线性化理论。这些模型和方法虽然可以近似地用以对机翼摇晃做局部分析或控制,但无法从全局角度对整个系统进行剖析,而且大多数还局限于固定迎角或迎角变化很小的情况下进行的,并不能真实地反映出战机实际飞行的振荡情况[24-32]。

3)深失速和尾旋研究

Garrard和Jordan[33]使用F-8“十字军”战斗机的纵向模型进行了分叉分析和分叉控制,模型假设飞机在高度为9 000 m、俯仰角很小的水平范围飞行；Montgomery和Moul[34]采用稳定坐标系下的纵向三自由度模型,并对模型作忽略大气密度假设和简化后分析深度失速问题；Powers[35]通过对“T”尾翼运输机的风洞试验研究了纵向俯仰深失速特性；Lee等[36]研究了54种飞机的升力系数在低雷诺数下的大迎角变化现象,并将其化分为5类:恢复(12%)、常态(33%)、急剧掉(36%)、跳跃(7%)、急剧掉与跳跃(12%),将影响升力系数变化的物理特性分为:最大厚度、拱形、后缘机翼角等；Montgomery和Moul[34]采用相平面技术分析了某“T”尾翼飞机非线性动力特性中导致深失速的因素,所得到的相平面轨线结果对定量分析深失速的改出边界具有指导作用；Meznarsie和Gregory[37-38]等也对这类问题进行了分析；Mehra和Carroll[39]提出了分叉分析和突变理论(Bifurcation Analysis and Catastrophe Theory Methodology,BACTM)方法,首次把BACTM应用于飞行动力学,并首次用连续算法分析了可变尾翼飞机和有后掠翼飞机F-4大迎角下的全局稳定特性,通过学习两架飞机的稳定状态发现由于配平稳定状态下的Hopf分叉引起失速迎角处出现了机翼摇晃,并对飞机将经历失速/尾旋等危险状态的舵面位置进行了预测；此后Carroll,Chen,Sibilski,Liaw,Cochran和Gates[40-45]等对分叉分析方法进行了一系列研究,结果表明分叉分析方法在计算平衡解或周期解的同时,也可以得到平衡面的稳定性,但是对需要多个舵面协调偏转的约束飞行,如定直飞行、定常盘旋及无侧滑盘旋及绕速度矢量滚转等,需要对分叉分析法进行推广；Young等[46]扩展了Gates和Minka的分析方法,得到扩展分叉分析法(Extended Bifurcation Analysis,EBA),分析了比较完整的模型(空气动力学模型为迎角非线性函数的五阶运动方程)的稳定状态,定量分析了飞机运动方程的全局特性,预测了由滚转耦合不稳定性引起的跳跃现象；Thomas等和Guicheteau[47-48]用分叉分析法和连续算法分析了包含不稳定气动导数的非线性飞机模型,并分析了重心的横向偏移和发动机陀螺力矩在尾旋进入和改出的影响等问题；Avanzini和 Matteis[49]采用分叉分析研究了放宽静稳定性后的F-16飞机,并对全权限飞行控制系统飞机的静态不稳定和边界稳定状态下有关问题进行了仿真；Marusak等[50]采用分叉理论和连续算法分析了喷气式飞机IRYDA和军用直升机PZLSOKOL的飞行临界状态,发现了喷气式飞机IRYDA稳定状态升降舵操纵会导致周期运动两个Hopf分叉产生；Lina和Moul[51]在高度为4 572 m和无推力的情况下用飞行模拟器对“T”尾翼飞机进行深失速研究,指出俯仰阻尼是深失速改出的重要指标—低俯仰阻尼比和负阻尼比对深失速改出是有利的。

4)过失速机动研究

过失速机动的理论是德国MBB公司先进战斗机部主任沃尔夫冈·赫伯斯特(Wolfgang Herbst)博士于20世纪70年代提出的。过失速机动是第四代和未来战机的典型特征。国际航空界给予高度重视,使得部分型号的三代机也具有不同程度的过失速状态飞行能力,如美国格鲁门公司设计的F-14战斗机在迎角40°～45°时仍能保持稳定的亚声速飞行；F/A-18战斗机失速迎角仅为37.5°,但却具有约55°迎角的配平能力,可瞬态进入60°以上的迎角,并且保持飞机在各轴向一定的控制能力；苏-27战机可以完成具有极高知名度的战术动作“眼镜蛇”机动等；美国为了验证过失速机动而研制的X-31、F-16MATV、F-18HARV以及YF-22等战斗机都具有过失速机动能力；第四代战斗机F-22采用气动舵面与推力矢量结合的控制手段,已经具有很完善的过失速机动能力。在过失速机动理论研究方面,Beh等[52]研究了X-31的大迎角方法和着陆控制律,并在线性和非线性的范围内对ESTOL(Extreme Short Take Off and Landing)控制律的稳定性和性能进行了分析；Sibilski[42]使用分叉分析方法对连续方法实现和控制律参数全局辨识问题进行了研究,认为研究这两种方法对分析飞机运动方程有一定的应用价值,可以用来分析更复杂的空气动力学模型,在设计中可以预测并改善飞机的动态特性；Atesoglu和Özgören[53]对应用推力矢量来加强大迎角战机的机动性能问题进行了研究,给出了单独应用空气动力学控制和单独应用推力矢量控制下眼镜蛇和赫伯斯特两种超机动仿真对比分析,综合建立了非线性六自由度非线性飞行动力学、发动机和推力矢量的数学模型,证明了在常规气动布局的基础上结合推力矢量技术,在大迎角状态下能有效地增加战机的机动性能；Jouannet和Krus[54]给出了大迎角状态下空气动力学的数学预测模型,该模型可以应用到飞机的概念设计,并且可以推广到根据风洞试验数据和实际飞行数据进行参数辨识过程中；Forsythe等[55]采用六自由度计算模型来估算F-15E进入旋转的机动动作,应用DES(Detached-Eddy Simulation)来预测机体周围大量分离的气流区域,并在9 144 m标准高度上计算了3种进入尾旋机动；Michal等[56]以F-16XL战机为模型,应用Flight Condition 7飞行试验数据,对基于BCFD(Boeing Computational Fluid Dynamics)和CAWAPI(Cranked Arrow Wing Aerodynamics Project Investigation)的大迎角状态下的研究结果进行了分析；Green[57]以F/A-18E战斗机为模型论证了CFD在预测飞机亚声速大迎角状态下的纵向稳定性和控制特性的适用性；Park等[58]应用三维可压缩Navier-stokes方程和k-ω SST(Shear Stress Transport)湍流方程计算了分析5°半锥角超声速飞机的大迎角空气动力学特性。

在防止深失速的控制方法研究方面,早期使用推杆到底和动态改出法——俯仰振荡法改出,它是基于李雅普诺夫方法的控制律,其基本思想是在深失速区域内有意识地造成扰动,使飞机能够从深失速吸引区中跳出来；Roberts和Strom[59]在大迎角时使用水平尾翼、前缘襟翼和发动机推力构成了全轴控制改出常规飞机的深失速,并针对推力矢量飞机提出了分支剪裁方法,改善了飞机大迎角区域内的分叉结构；Goman等[60]将分叉控制与最优控制相结合,使得飞机非线性稳定平衡点的吸引域最大化,提高了系统对大扰动的鲁棒性,结果表明了分叉控制在非线性控制中的巨大潜力；Lowenberg[61]利用分叉分析方法研究了飞机偏离稳定性和控制问题；Littleboy和Smith[62]利用分叉分析和动态逆方法改进了非线性控制律的设计。

国内研究主要是跟踪国外的研究,如高浩、陈永亮等[63-64]对机翼摇晃预测与抑制问题进行了研究；周晓欲和余勇军等[65-66]为了构造深失速走廊采用反向积分技术,对F-16飞机机体坐标下的纵向运动方程做了速度和航迹角不变的假设,将其简化为二阶短周期运动模态的模型；郑贤芬等[67]建立了“T”型尾翼飞机的闭环特性计算数学模型,应用时间历程法讨论了“T”型尾翼飞机的深失速开环特性,分析了气动力矩特性和升降舵操纵规律对深失速改出特性的影响；程泽荫[68-69]应用BACTM方法对Y7-200B飞机的失速特性进行了分析,同时对波音公司的控制飞机失速特性的纵向力矩“勺形”区宽度和深度指标进行了验证,详细地分析了Y7-200B/A飞机的纵、横航向静稳定性；王大海等[70]用分叉分析法分析了飞机全局稳定性,用四阶龙格-库塔积分计算飞机运动的平衡点和分歧点,构造运动状态的扰动传播矩阵,并利用扰动传播矩阵求得满足规定的飞机反应特性所需的操纵,即各操纵面反馈回路的放大系数值；黎康和方振平[71-72]用分叉分析方法研究了大迎角非线性动力学系统的结构稳定性问题,通过合理选择平衡点线性化方程,采用特征结构配置方法设计调参的大迎角控制律,以使飞机的稳定飞行状态可延伸至大迎角范围；陈永亮等分别设计了深失速改出控制规律。

近年来,国际航空界对飞机过失速机动进行了一系列研究,Zanotti,Wang和Visbal等采用数值方法对动态深失速现象的流动特性进行了建模和分析[73-75]；范丽和辛琪等采用静态分支和动态分支进行解析和数值分析研究了大迎角飞行的稳定性问题[76-78]。

根据以上分析可见,国内外的飞机大迎角分析主要依赖于风洞试验和简化模型而展开,多数研究者都是对风洞试验结果建模进行稳定性等分析,没有对试验条件限制、分析方法本身的缺陷、模型不准确或过度简化产生的安全性隐患等问题进行系统研究。直至目前,很多大迎角特性是飞行员试飞出来的,而不是根据系统分析和自动控制系统实现而得到的,理论方法还不能科学预测和运用飞机大迎角性能并保证飞行安全,高性能飞机研制水平仍然在很大程度上依赖于试飞员。因此,系统研究飞机大迎角不确定模型下的非线性分析、预测、控制方法和实现仍然是当前和今后航空界研究的重点内容。

1.1 常用操纵稳定性飞行试验方法回顾

操纵稳定性飞行试验的目的是为了建立飞行器的数学模型,飞机模型实际上是一个很复杂的非线性微分方程式,人们很难得到准确的数学模型。工程上为了简化问题,在给定高度和马赫数(类似于研究三极管放大特性时给定工作点)条件下对模型进行线性化处理,试飞员在无剩余推力下首先保证飞机在给定高度和马赫数下平飞,再给飞机操纵杆机动动作(通常为脉冲、倍脉冲或3211动作)激励,然后使得飞机自由运动回到平飞状态,获得飞机在高度和马赫数下的操纵稳定性试验数据,再根据式(1)～式(4)使用系统辨识方法确定气动参数。

对于飞机纵向运动而言,在给定高度、马赫数下的小扰动状态方程通常为

式中:q为俯仰角速度；α为气流迎角(攻角)；ϑ为俯仰角；V0为空速；φ0为给定高度和速度飞行时的滚转角平均值；nx和nz分别为纵向和法向过载；δe、δc和δL分别为升降舵偏角、鸭翼偏角和其他舵偏角；g为重力加速度；Xq、Xα、XV、XδL、、Zq、Zα、ZV、Zδe、ZδL和Zδc分别为纵向和法向气动力系数；Mq、Mα、MV、Mδe、Mδc和 MδL为气动力矩系数、和分别为q、α、ϑ和V0的估计值；bq、bα、bθ和bV为状态方程模型偏差、、、和为观测方程模型偏差,模型用度作为单位。

在给定高度和马赫数下的飞机横航向小扰动状态方程通常为

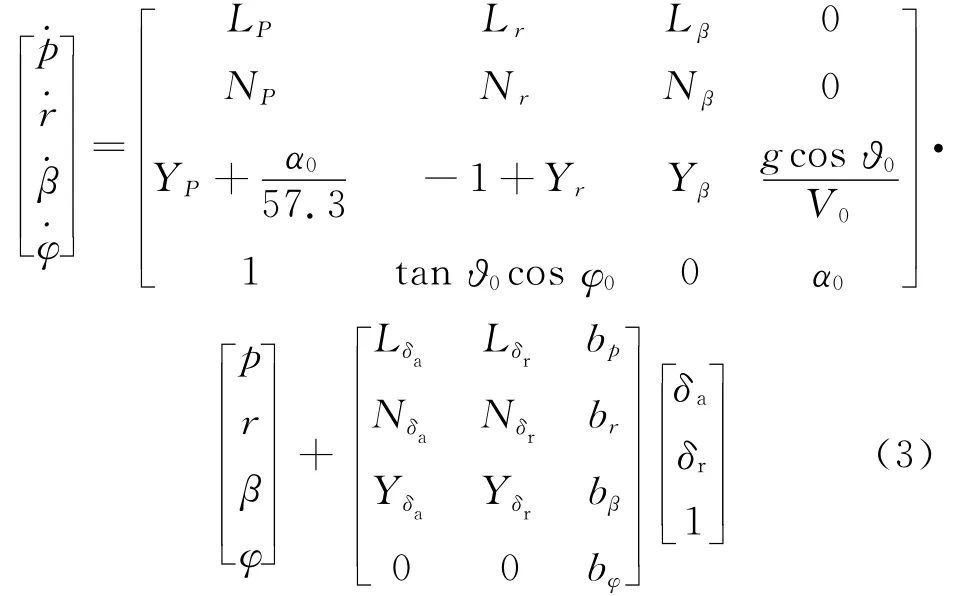
观测量可选p、r、β、φ和侧向过载ny作为观测量,p、r、β、φ 的表达式与q、α、ϑ、V0类似,ny的表达式为

式中:p、r、β和φ分别为滚转角速度、偏航角速度、侧滑角和滚转角；δa和δr分别为副翼和方向舵偏角；Yp、Yr、Yβ、Yδa和Yδr为侧向气动力系数；LP、Lr、Lβ、Lδa、Lδr、NP、Nr和Nβ为气动力矩系数；bp、br、bβ、bφ和by分别为状态方程和观测方程偏差；ϑ0和α0分别为给定高度和速度飞行时的俯仰角和气流迎角,模型用度作为单位。

这样通过一系列飞行试验就可以获得飞行器的网格点模型。

因此,飞行试验所得模型可以统一描述为

在给定第i高度为H(i)、马赫数为Ma(i)时,飞行器的状态方程为

式中:xi为给定第i高度为H(i)和马赫数为Ma(i)时的状态变量；Ai和Bi分别为已知系统矩阵和控制矩阵；ΔAi和ΔBi为模型描述以及飞行试验、系统辨识带来的系统矩阵和控制矩阵建模误差。

飞行控制器的设计任务就是根据式(5)设计若干个飞行控制器,使得飞行器在包线内达到稳定裕度等性能指标。

在经典飞行控制器设计中,将式(5)飞行器模型简化为

在给定第i高度为H(i)、马赫数为Ma(i)时,飞行器的状态方程为

然后根据式(6)设计若干个飞行控制器,使得飞行器在包线内达到稳定裕度等性能指标,这种模型对静稳定性较好的飞行控制器设计很实用。

40多年以来,随着非线性控制理论得到飞速发展,国际航空界已将有关成果用到飞行控制系统的设计中,许多飞行控制学者在非线性控制领域进行了深入研究,取得了比较突出的成果。特别是德国宇航院和美国NASA所做的研究工作尤为突出。通常采用的方法有以下几种:

1)数值优化法:数值优化法根据飞机所要完成的机动动作的要求,建立目标函数及约束条件,通过求极值来解出飞机的飞行规律,完成控制系统的设计。

2)微分几何法:微分几何在非线性系统中所取得的成功有如1950年后的拉氏变换和复变函数之于单输入单输出系统,1960年后的线性代数之于多输入多输出线性系统。该方法应用微分流形概念,借助于构造微分同胚变换和反馈变换可以实现非线性系统的完全精确线性化。

3)滑模变结构设计方法:滑态是全状态空间中的一个子空间,一旦系统进入滑动状态,就将永远保持在其中。

4)动态逆设计方法。非线性控制的动态逆设计方法在理论上已经比较成熟,广泛应用于飞行控制系统的设计中。该方法要求系统的输入和输出变量相同,在飞行控制系统设计中,可以通过时间尺度来解决。动态逆方法由于具有直观、简明、对应用模型所作的限制少等特点,被广泛应用于飞行控制等领域。

对于飞机过失速机动的大迎角飞行问题,则需要对进行输入设计、非线性模型进行结构和参数辨识和模型验证后,才能得到工程使用的飞机模型[79],目前的控制理论也不能给出飞行控制的统一设计方法。

1.2 鲁棒飞行控制器研究问题

飞机鲁棒控制研究具有重要的理论和工程意义。现代和未来的战斗机为了提高“机敏性”都放宽了对飞机静稳定性的限制,飞机通常要求在开环临界稳定点附近工作,这样就要求飞行控制系统能良好地处理所谓模型不确定性问题。在实际飞行控制系统设计中还要考虑以下问题:

1)在已经建立起数学模型的飞机参数发生变化或存在结构不确定时,飞行控制系统应该具有小的灵敏度响应。

2)由于控制器频带比较宽,使得飞机性能受飞机结构和执行机构动态性能变化的影响的灵敏度响应比较大。

3)反馈控制器的设计虽然对飞行员指令会得到较理想的响应,但是对于外部干扰的响应可能会是破坏性的。

4)执行部件与控制元件存在制造容差,系统运行过程中也存在老化、磨损及环境和运行条件恶化等现象。

5)在实际工程问题中,通常对数学模型要人为地进行简化,去掉一些复杂的因素。为此,在研究现代飞机的控制问题时,就必须考虑鲁棒性问题。

1990年以来,国际上对鲁棒飞行控制和智能飞行控制问题展开了广泛研究。H∞由加拿大学者Zames提出的。Zames认为,基于状态空间模型的LQG方法之所以鲁棒性不好,主要是因为用白噪声模型表示不确定的干扰是不现实的。因此,在假定干扰属于某一已知信号集的情况下,Zames提出用其相应灵敏度函数的H∞范数作为指标,设计目标是在可能发生的最坏干扰下使系统的误差在这种范数意义下达到极小,从而将干扰抑制问题转化为闭环系统稳定性设计问题。从此,国内外很多学者展开了H∞控制方法研究,为了便于计算,出现了LMI方法,以后又出现了μ综合方法等。鲁棒控制方法在航空界一直处于探索阶段,美国NASA、德国宇航研究院以及荷兰等国都对鲁棒控制方法进行了研究,取得了很多仿真和实验结果。国内的航空院校也对飞机鲁棒控制方法进行了一系列的研究。但这些结果与实际应用的距离还相差甚远。

作者认为,鲁棒控制器设计方法应该主要开展以下研究:

1)模型不确定系统的鲁棒控制方法研究。该研究主要是为了解决风洞试验、飞行试验给出的飞机模型结构和参数不确定问题。

2)时间滞后系统的鲁棒控制方法研究。该研究主要是解决反馈测量量如气流迎角和侧滑角等给系统带来的不确定的时间滞后问题。

3)区间系统的鲁棒控制方法研究。通常,飞机控制是按不同的高度和马赫数构成一系列控制器,然后根据飞行状态进行切换。该项研究主要是为了寻求控制器的最小个数,确保控制器切换时的稳定性和整个飞行区域的稳定性。

4)不稳定系统的鲁棒控制问题。由于现代和未来战斗机都放宽了静稳定性,高性能飞机的开环模型在某高度、马赫数的范围内是不稳定的,而在其他区域稳定。为此,就需要研究不稳定系统的鲁棒控制问题。

5)飞机姿态和快速瞄准鲁棒控制。现代和未来战斗机必须考虑快速瞄准敌机的能力并具有很高的机敏性,飞机模型等存在种种不确定因素时,所设计的控制器能否使飞机保持这种能力需要研究。

6)输入、状态受限制的鲁棒控制。现有的鲁棒控制理论与方法大多数都没有对系统状态和输入的大小进行限制,而飞机的操纵舵和飞行状态都有限制。如线性矩阵不等式(LMI)方法不具备完备性,只给出了不等式而没有给出不等式的存在条件。

7)多输入多输出(MIMO)系统的稳定裕度控制。如何满足军标的稳定裕度要求,需要从鲁棒性的角度来考虑。

8)阵风干扰下的鲁棒控制。当飞机遇到阵风等干扰时,如何进行控制需要研究。

1.3 飞机大迎角飞行需要解决的控制问题

飞机大迎角飞行时,飞机运动方程为高度复杂的不确定非线性系统,存在多种混合的非线性运动现象。为了系统分析、预测和控制这些非线性现象,揭示飞机的全局飞行动力学特性,应该系统地对以下3个方面问题展开深入研究:

1)具有多平衡点、突变等飞行试验建模问题。过失速机动飞机本身是具有跳跃等复杂的非线性、时变的动力学系统,飞行的气动参数会随高度、马赫数、迎角、侧滑角以及操纵面偏转的变化而变化,较常规飞机而言,这种变化幅值和速率要大得多,并且4代机一般均具有鸭翼等非常规控制舵面,因此利用经过非线性辨识的气动导数构建大迎角机动动力学模型非常重要。为了发挥战机性能,需要根据实际舵面的控制条件研究扩展包线推力矢量等飞机动力学建模,建立完善的推力矢量飞机含过失速机动扩展包线的总体模型,飞机的低速大迎角和特大迎角区域如给出推力矢量力和力矩在三轴上的数学模型,推导单发与双发战斗机带三轴推力矢量飞机的非线性运动方程,为控制律设计奠定基础。该研究涉及试验中的充分激励问题、模型优选判据和优选算法、模型验证问题、模型分离问题、数据预处理与参数辨识问题以及不确定系统的估计问题等。

2)过失速机动时飞机模型不确定非线性控制问题。过失速状态下的飞机带有复杂的不确定性,这种不确定性既包括自身建模过程中的不准确性,还包括了外部飞行环境的扰动,这些都使得飞机模型具有快时变、强非线性、强耦合和不确定性等特点,尤其是有些突变问题在模型中也未反映出来。采用何种非线性控制方法解决飞机模型的强非线性、强耦合、快时变和多变量等问题,同时还能够抑制不确定性因素,保证系统的足够的稳定性和安全性,将是过失速机动飞行控制的关键问题。基于试验模型的鲁棒稳定性分析、飞行中的分叉、混沌等特殊现象分析、能量和输入受限制的不确定大迎角模型的稳定性控制问题等。

3)过失速机动时飞行轨迹和姿态协调控制问题。大迎角状态下,飞机的动态对飞行条件的变化异常敏感,任何飞行轨迹的变化都将直接影响到飞机推进系统的效率、飞行的气动特性以及机体结构特性,所以为了确保飞机高机动性和操纵性,必须深入研究具有高精度高带宽的协调控制方法,实现飞机混合异类多操纵面的复合控制,优化超机动飞机不同模态之间的运动关系,实现飞行轨迹与飞行姿态之间的协调控制,使得过失速机动飞行时在所有的飞行阶段上都能有效、安全地从一个飞行目标达到另一个飞行目标,顺利完成预定的飞行任务。

为此,在大迎角模型建立过程中,不仅要考虑常规布局战机,还要考虑非常规布局或加入特殊控制舵面或翼形的战机和应用推力矢量的新型战机。并且,还要充分考虑飞行试验中所出现的各种非线性现象,如机翼摇晃、深失速、尾旋、纵向跳跃、混沌和长周期振荡等,力求最后模型能精确仿真出其中多数危险机动动作所带来的不利影响。并把建立的模型用实际飞行数据进行大量的测试,从而进行修正完善。另外,鉴于以往大迎角建模,比如横侧向机翼摇晃和纵向深失速,一般是在假定横纵解耦的条件下即进行了大量的简化后进行的,为了提高模型精度、可信度以及对实际飞机设计和控制方面的参考和指导意义,有必要在更高维甚至全维的基础上来进行模型的建立。除此之外,模型建立过程中的参数辨识,不可避免地会带来一定程度的精度损失,极有可能使所建立的模型掩盖了一部分边缘危险,因此有必要对所建立的模型在合理的误差带范围内进行摄动分析,最大限度地探测出实际战机高超机动所潜伏的非线性危险,如振荡跳跃和长周期振荡等。由于大迎角飞行情况下的诸多不确定性,某一特定非线性现象的分析和控制器往往与实际响应差异很大,设计控制器时要立足于大迎角模型充分的非线性分析基础之上,能抑制各种非线性现象所隐含的潜在危险。

2 大型运输机超低空重载空投或飞行故障对突变控制理论的挑战

大型运输机在超低空重载空投过程中,驾驶员的反应往往存在偏差,不能在时间上精确地进行控制器切换,以至于控制器的切换会发生超前或者滞后,而控制器切换超前或者滞后易使飞机姿态发生剧烈振荡,从而诱发飞行高度的较大波动,容易造成机毁人亡。该问题属于突变模型的控制问题。

2.1 大型运输机超低空重载空投

现代化战争具有突发性强、作战节奏快、作战强度大、物资消耗大和时效性高的特点,以大型军用运输机为主体的空中运输可快速、灵活、有效地保障作战人员和物资的供应,能快速远距离提供机动能力,成为部队战略开进和快速部署的重要支柱。

在战争中,军用运输机的主要任务是空运军事人员、散装货运(包括食品、医药和弹药等)、大型车辆(包括卡车、吉普车、装甲车、防空车和小型直升机等)、特大型车辆(包括坦克、大炮、工程和建筑设备、大型卡车和面包车、大型货运直升机)等。急需大型军用运输机为预警指挥机、加油机和电子战飞机等特种作战飞机提供空中载机平台。

现代战役中,大型运输机的重要作用体现在3个方面:实施部队的快速部署和机动；实施战役纵深的空投空降；执行战场持续保障支援任务。及时快捷地输送大量作战人员、武器装备和给养,实施大规模的空投、空降,对敌入侵做出快速反应；有了大型运输机,中国才拥有改装各种特种飞机的空中平台,进而才能有效地实施电子侦察、电子干扰和电子对抗,给陆、海、空三军提供高科技时代最基础、最基本的攻防手段。

作为低空飞行的典型任务,超低空重装空投具有空投质量大、效率高的优点,但飞机在进行超低空重装空投时,因货物后移将引起迎角、俯仰角速度的不断增大,在货物出舱瞬间尽管俯仰角速度将减小,但只有在角速度减小到零附近时,迎角才基本停止增大,同时货物出舱瞬间将引起空投模型的突变,因而要保障飞机超低空重装空投安全,需解决低空大迎角运动和模型突变时的安全控制问题。

目前,运输机己经成为各国空军必须装备的重要机种之一。不但美国、俄罗斯这样的大国研制并装备了大量运输机,而且欧洲国家也打算研制并装备A400M运输机,以便打破美国在军用运输机领域的垄断地位。中国的台湾地区及周边的日本、印度虽然不具备研制大型军用运输机的条件,但是它们从美国、俄罗斯积极引进了伊尔-76、C-130等运输机,从而使部队的机动作战能力有了很大提高。在现役的军用运输机中,C-5、C-130、C-17和伊尔-76最具有代表性。其中,美国洛克希德·马丁公司研制的有C-5、C-130和C-17。C-5具有座舱现代化,并安装包括GPS、卫星通信和甚高频数据链在内的通信导航系统。C-130中型运输机自1954年研制成功以来已有40多种改型,能执行多种作战任务。C-17是美国最新研制的重型运输机,由于该机同时具有载重量大和起落性能好的特点,使它能够同时承担战略运输和战术运输的任务。

伊尔-76是俄罗斯伊留申航空联合体研制的重型运输机,其外形和载重能力都类似于美国的C-141。通过改进改型,伊尔-76已经发展了10余个型别,而且伊尔-78空中加油机、A-50预警机、伊尔-82空中指挥机和伊尔-84远程搜索救援飞机也都是以伊尔76为平台研制的。俄罗斯和乌克兰联合研制的中型运输机安-70是世界上第一种采用桨扇发动机、并达到实用阶段的飞机。机上的电子设备包括导航和气象雷达、多普勒自动导航系统、敌我识别系统、塔康和无线电通信电台等。西欧国家也在可以购买美国飞机的情况下决定研制欧洲人自己的A400,它是空中客车军事公司目前正在研制的中型运输机,主要用来取代欧洲国家目前使用的C-130和C-160运输机。

长期以来,对超低空空投系统的设计研究较多,但对于高空重载空投过程的建模和控制飞行试验方法的研究还比较欠缺。在建模方法上,由于缺乏系统的、精确的理论分析,主要依靠设计人员根据简单的数学模型,凭借经验进行初步设计,难以准确评估飞机安全性和冲击载荷的大小。

重型货物投放瞬间会使运输机重量、质心及惯性矩产生突然变化,飞行器数学模型瞬间发生突变[80-84]。通常情况下,人们根据不同的飞行状态设计不同的控制器,飞行条件发生变化控制器也随之切换,以完成控制任务。在空投任务中,驾驶员的反应往往存在偏差,不能在时间上精确地进行控制器切换,以至于控制器的切换会发生超前或者滞后,使得飞机姿态发生剧烈振荡,从而飞行高度发生较大波动,在这种情况下控制器的设计必须满足一定条件,保障空投过程的飞行稳定,否则极易发生严重的飞行事故。

针对重型货物离机突变过程建立非线性数学模型,将此过程分为前后2个状态:①重型货物离机前即货物已经移至舱内尾部阶段；②重型货物离机后即货物已经移出机舱,此时运输机的数学模型瞬间发生突变。进而在2个状态下分别建立运输机六自由度非线性动力学模型,并将运输机非线性方程输入输出反馈线性化。由于运输机空投突变过程中其数学模型发生突变,载机飞行高度及飞行姿态会发生较大波动,为了解决飞机的高度与姿态控制问题,所以根据飞机的状态方程,选择高度和俯仰角这两个状态变量作为控制变量。

如果控制器切换超前,则在超前时间段内为空投前的模型在空投后模型的控制器下工作,将待求投放后控制律代入空投前模型系统表达式；同理,如果控制器切换滞后,则在滞后时间段内为空投后的模型在空投前模型的控制器下工作,将待求投放前控制律代入空投后模型系统表达式。由于需要在控制器切换错误情况下仍能保持系统的稳定,即在控制器切换超前时间段内闭环系统稳定且其振荡较小,在控制器切换滞后时间段内闭环系统稳定且振荡较小。

宽适应性设计要求控制器在切换错误时间内,其对应模型的动态响应不会发生较大振荡。即当设计控制器使空投前闭环系统模型具有最佳响应同时应使第2个模型渐近稳定且振荡较小,同样在设计控制器使空投后闭环系统模型具有最佳响应同时应使第1个模型渐近稳定且振荡较小,这样能保证在控制器切换错误时间内,系统响应不发生剧烈振荡。

通过研究超低空重载空投宽适应控制策略解决模型突变问题,采用一个控制器对整个突变过程进行控制,从闭环系统稳定性角度出发,通过对突变前后2个系统的黎卡提方程进行联立约束:

式中:Q1、R1、Q2和R2为需要选定的正定矩阵；P1和P2为需要求解的正定常矩阵；A1、A2、B1和B2为投放前和投放后系统矩阵和控制矩阵。式(7)和式(8)满足:

2)在控制器超前切换时间段Δt内,闭环系统1 由 ˙x1=(A1-B1R-11BT1P1)x1切 换 至 ˙x1=(A1-B1R-12BT2P2)x1和由˙x1=(A1-B1R-12BT2P2)x1切换至˙x2=(A2-B2R-12BT2P2)x2的响应稳定且振荡不能过大,即要求Re[eig(A1-B1P2)]＜0,且其复特征根阻尼比较大。

3)在控制器滞后切换时间段Δt内,闭环系统2 由 ˙x1=(A1-B1P1)x1切 换 至 ˙x2=(A2-B2P1)x2和由˙x2=(A2-B2P1)x2切换至˙x2=(A2-B22)x2的响应是稳定的且振荡不能过大,即要求Re[eig(A2-B2P1)]＜0,且其复特征根阻尼比较大。

进而完成闭环控制器的优化求解,该宽适应控制策略的优点是在驾驶员反应时间存在不确定情况下,控制器仍能保证内环飞行速度与姿态具有良好动态响应,结合外环高度控制系统,实现了空投过程中飞行姿态与高度的平稳过渡,保证了空投突变过程的安全。

今后对于超低空重载空投研究中,需要考虑飞机输入和状态等限制条件、地效、阵风干扰、模型变化及不确定、颤振等各类情况,按照具有平稳无超调裕度的宽适应性设计方法设计飞行控制器,使得针对空投前或空投后的两个控制器无超调,空投前的控制器在切换滞后时能平稳响应,空投后的控制器在切换提前时能平稳响应,从而保证了超低空重载空投过程中的飞行安全。

2.2 飞机发生故障的突变控制问题

飞行器系统的故障诊断研究已经越来越受到人们的重视；故障诊断对于安全性要求高的系统极其重要,及时地检测出系统故障,使自修复系统及时重构控制律,可避免系统崩溃及由此造成的物质损失和人员伤亡。

以解析冗余为主导的故障检测与诊断技术是从20世纪70年代初首先在美国发展起来的。1971年,美国麻省理工大学Beard在他的博士论文中首先提出了用解析冗余代替硬件冗余,并通过系统自组织使系统闭环稳定；通过比较观测器的输出得到系统故障信息的新思想,标志着基于解析冗余的故障诊断技术的诞生。国外对于故障诊断的研究主要集中于工业系统和航空航天系统,目前以研究广义系统和非线性系统的故障诊断为主,采用的方法非常多样,具体有滑模观测器方法、神经网络方法、专家系统方法、小波变换方法和未知输入观测器方法等,并多将几种方法结合起来使用。对于线性系统和有关传感器的故障诊断方法已经比较成熟,已经有一套比较完整的诊断方法,并已经有一些实际的应用系统。

航空工业界非常重视飞机本身的故障诊断和健康预测管理系统研究,并且在现代运输机和战斗机等飞机上采用了多余度和自修复技术。对飞机机电等系统故障诊断和健康管理的研究,不仅可有效地提高飞机的可靠性,减少故障的发生,还可降低使用和维护费用,提高任务出勤率。以飞机机电系统为例,发动机、环境控制、起落架、飞机燃油、液压系统、供电系统、机轮刹车系统、第2动力、外挂吊舱、生命保障和弹射救生等系统如果出现故障,如何进行应急控制,以保证飞行安全。

故障发生过程模型都会发生突变。因此,当飞行器自身出现故障时,整机气动力、力矩、参数和输入量都可能发生变化,如飞机机翼穿透一个小孔就会导致全机所有的气动力和力矩等突变,而且不同的机动动作会增加一个等效输入[85-98]；然而,目前的理论研究方法主要以将飞行器出现故障前后的模型用相同的结构和参数来描述,仅仅对输入系数等参数进行调整,设计中没有考虑空气动力学特性,导致给出的容错控制方案脱离实际飞行器而难以应用。

对于飞行器三维运动非发动机空中停车等必须应急或迫降的其他故障诊断和容错控制而言[99],飞行器无故障时三维运动的非线性模型为

式中:h和VT分别为飞行高度和飞行速度；Q、S、m、Ix、Iy、Iz和Izx分别为动压、机翼面积、飞行器质量、绕机体轴系x轴的转动惯量、绕机体轴系Y轴的转动惯量、绕机体轴系z轴的转动惯量以及机体轴系xz 轴的惯性积；Cx(α,β,δ)、Cy(α,β,δ)和Cz(α,β,δ)分别为纵向力、侧向力和法向力；CL(α,β,δ)、CN(α,β,δ)和 CM(α,β,δ)分 别 为 滚转力矩、偏航力矩和俯仰力矩；δ为控制量；通常侧滑角小于90°,cosβ不会为零。

故障检出方法为:当状态组合指标J≥1,则判定飞行器有故障,其中:

式中:hpre(i)、VTpre(i)、αpre(i)、βpre(i)、Ψpre(i)、φpre(i)、ϑpre(i)、ppre(i)和qpre(i)和rpre(i)分别为根据式(9)在时间t=i T(i=k,k+1,…,N)计算得到的h、VT、α、β、Ψ、φ、ϑ、p、q 和r 值；hout(i)、VTout(i)、αout(i)、βout(i)、Ψout(i)、φout(i)、ϑout(i)、pout(i)、qout(i)和rout(i)分别为在时间t=i T(i=k,k+1,…,N)实际测量得到的h、VT、α、β、Ψ、φ、ϑ、p、q和r值；Δht、ΔVTt、Δαt、Δβt、ΔΨt、Δφt、Δϑt、Δpt、Δqt和 Δrt为设定的检测阈值；sign(x)为符号函数:当x＞0时为1,其余为0；k表示第k个采样点,对应采样时间为t=k T；N为设定误差累计个数；T为采样周期。

飞行器出现故障时首先对故障分类,再针对确定的故障类别分析飞行器全机参数和飞行动力学特性的影响,然后重新对故障发生后突变系统建模,得到飞行器出现故障时三维运动的非线性模型描述为

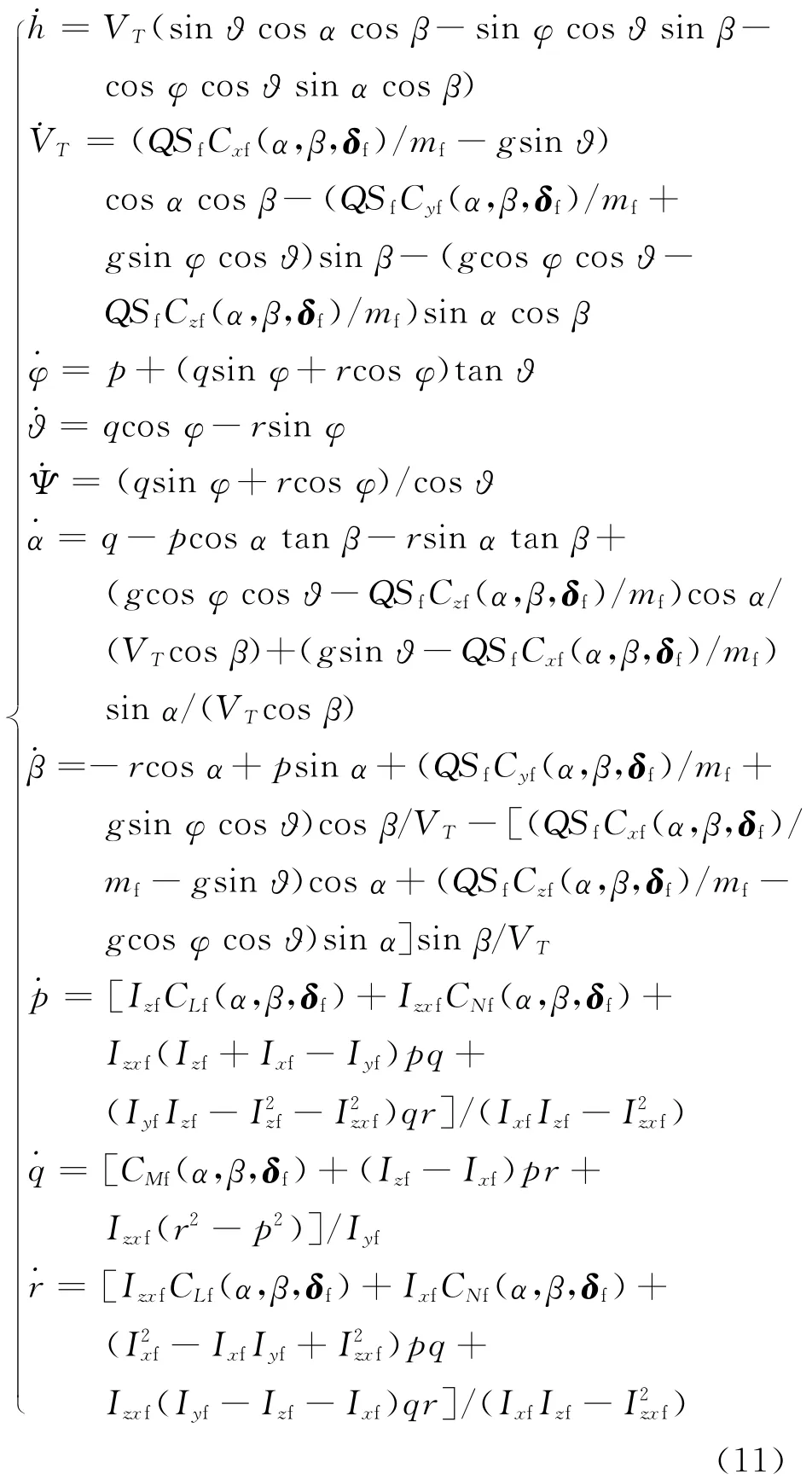
式中:Sf、mf、Ixf、Iyf、Izf和Izxf分别为飞行器出现故障时的机翼面积、飞行器质量、绕机体轴系x轴的转动惯量、绕机体轴系y轴的转动惯量和绕机体轴系z轴的转动惯量和机体轴系xz轴的转动惯量积；Cxf(α,β,δf)、Cyf(α,β,δf)和Czf(α,β,δf)分别为飞行器出现故障时的纵向力、侧向力和法向力；CLf(α,β,δf)、CNf(α,β,δf)和 CMf(α,β,δf)分别为飞行器出现故障时的滚转力矩、偏航力矩、俯仰力矩；δf=[δ δapf]T为飞行器出现故障时的控制输入,δapf为飞行器故障引起的非人为附加控制量。

容错控制器的设计方法为:设计出的控制量δ使得非线性模型式(9)稳定裕度达到军标要求,且该控制量δ和飞行器故障引起的非人为附加控制量δapf共同组成的飞行器出现故障时的控制输入δf=[δ δapf]T使得非线性模型式(11)输出稳定。

3 姿态估计误差对飞行控制仿真验证的挑战

飞行控制的效果主要依赖于较准确的测量,在给定的测量精度下,很多控制方法的精度基本相同,即使使用经典的频率法也可以达到较好的控制效果。

空间运动体的姿态、位置和速度等状态输出是控制系统或地面指挥者所需的基本数据,对空间运动体的平稳性和安全性有重要作用。

对于舰载战斗机和无人飞行器的离舰/着舰而言,只有保持飞行姿态平稳且与沿着甲板跑道平行飞行,才可以避免飞机与甲板碰撞；飞机起飞着陆时,也必须保持飞行姿态平稳且对准机场跑道平行飞行,否则就会出现事故；对于无人驾驶的飞机而言,不仅起飞着陆等过程的姿态正确与否直接决定飞行安全,而且在巡航飞行时由于没有驾驶员感受飞行姿态也会使无人机偏离预定飞行轨迹甚至坠毁。

对于无人驾驶飞机而言,常常使用微机电系统(Micro-electromechanical Systems,MEMS)等器件构成的惯性测量单元(Inertial Measurement Unit,IMU)或姿态方位参考系统(Attitude and Heading Reference System,AHRS)。发动机产生的振动对惯性测量器件造成较大的测量误差,尤其是活塞式发动机常常使得MEMS器件精度显著减小,使得姿态估计出现较大的误差造成控制舵机的方向舵机的方向性错误,使得无人机事故频繁发生。国际上现在都十分重视无人驾驶飞机,但要脱离地面人员遥控操作进行自主飞行,使用活塞式发动机或使用MEMS器件导航无人飞机还难以实现[100-110]。微型飞行器超低空复杂地形飞行、仿生飞行及相关研究,大型高精度惯性设备通常无法安装,姿态直接可视化测量可以获得基本测量数据。

四旋翼无人机由于机动能力较差,测量仪器问题不是很突出,但是要对固定翼或单旋翼战术无人机等现代高性能无人机研究,必须选择测量系统。作者在临界稳定性的无人机飞行试验中,测量准确性问题难以解决,因此与中航工业618所共同设计了新的测控系统。

飞行控制器需要经过大量的地面“铁鸟”调试和飞行试验,特别是对于现代的静不稳定和多个操纵舵面的飞机,需要飞行试验次数更多。

在飞行控制方法研究中,由于不涉及测量问题使得飞行控制的研究结果严重背离实际,使得飞行仿真器难以接近实际,限制了实际飞行试验研究和新型飞机设计发展。目前大多数研究工作中的飞行控制器设计过程中的仿真与真实飞机飞行具有以下差异,如图1所示。

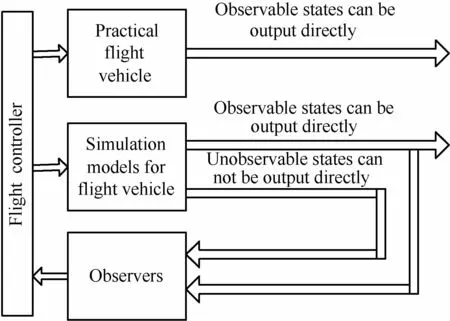
图1 飞行控制器仿真与真实飞机飞行的差异Fig.1 Differences between simulations of flight controller and real aircraft

飞行控制器设计过程中的仿真计算没引入真实飞机飞行状态输出的对比,即使引入所谓的“观测器”,也非真实飞机输出,仿真计算误差、实际测量误差等都与真实飞行不符；很多研究都不是发动机在无剩余推力及其他输入、状态受限情况下进行仿真,因此限制了研究结果对现代高性能飞机飞行控制器设计的指导作用。

当测量完全准确时,数字仿真也存在问题。例如著名的欧拉方程为

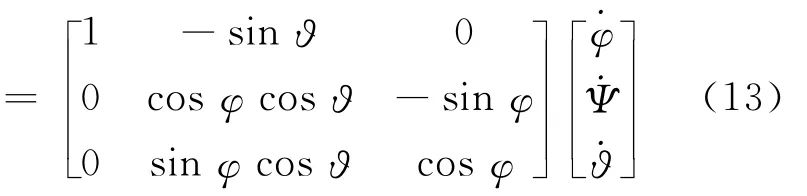
读者只要首先给定3个姿态角机动的动态过程,然后通过式(13)计算出三轴角速度,再代入式(12)积分对比姿态角的结果就可以发现仿真计算中的部分问题。

从事飞行控制器方法的研究人员如果能够对固定翼或单旋翼战术无人机进行实际飞行试验,就更能对自己研究的工作定位。

4 结 论

1)本文根据笔者30余年来飞行试验研究的实践,从实际飞行角度对影响飞行安全的大迎角过失速机动、超低空重载空投、飞行器突发故障和无人机控制方法研究作了简单综述,指出了飞行控制方法研究的方向和仿真研究存在的部分问题。

2)建议国家自然科学基金等重点支持结合实际飞行的飞行控制方法研究,无人机控制方法主要支持固定翼或单旋翼战术无人机等高层次研究,以便促进我国高性能飞机和高端战术无人机的发展。

[1] Phillips W H.Effect of rolling on longitudinal and directional stability,NASA TN-1627[R].Washington,D.C.:NASA,1948.

[2] Mehra R K,Kessel W C,Cnrroll J V.Global stability and control analysis of aircraft at high angle of attack,annual technical report 1,ONR-CR215-248-(1)[R].Cambridge:Scientific Systems Inc.,1977.

[3] Liefer R K.Fighter agility metrics,AD-A224-477[R].Virginia:ASTIA,1990.

[4] Jahnke C C.On the roll-coupling instabilities of high performance aircraft[J].Philosophical Transactions of the Royal Society A-Mathematical Physical and Engineering Sciences,1998,356(1745):2223-2239.

[5] Goman M G,Zagainov G I,Khramtsovsky A V.Application of bifurcation method to nonlinear flight dynamics problem[J].Progress in Aerospace Sciences,1997,33(9-10):539-586.

[6] Modi A,Ananthkrishnan N.Multiple attractors in inertia-coupled velocity-vector roll maneuvers of Airplanes[J].Journal of Aircraft,1998,35(4):659-661.

[7] Liebst B S,Nolan R C.Method for the prediction of the onset of wing rock[J].Journal of Aircraft,1994,31(6):1419-1424.

[8] Go T H,Ramnath R V.Analytical theory of three degree-of-freedom aircraft wing rock[J].Journal of Guidance,Control,and Dynamics,2004,27(4):657-664.

[9] Hsu C H,Lan C E.Theory of wing rock[J].Journal of Aircraft,1985,22(10):920-924.

[10] Ericsson L E.Wing rock analysis of slender delta wings,review and extension[J].Journal of Aircraft,1995,32(6):1221-1226.

[11] Arena A S J,Nelson R C.The effect of asymmetric vortex wake characteristics on a slender delta wing undergoing wing-rock motion,AIAA-89-3348-CP[R].Reston:AIAA,1989.

[12] Morris S L,Ward D T.A video-based experimental investigation of wing rock,AD-A218-244[R].Virginia:ASTIA,1989.

[13] Hall R M,Frate J H D.Interaction between forebody and wing vortices-a water-tunnel study,AFWAL-TM-85[R].Riverside:Air Force Wright Aeronautical Lab(AFWAL),1986.

[14] Takashi M,Shigeru Y,Yoshiaki N.The effect of leadingedge profile of self-induction oscillation of 45 degree delta wings,AIAA-2000-4004[R].Reston:AIAA,2000.

[15] Owens B O,McConnrll J K,Brandon J M,et al.Transonic free-to-roll analysis of the F/A-18E and F-35 configurations,AIAA-2004-5053[R].Reston:AIAA,2004.

[16] Elzebda J M,Mook D T,Nayfeh A H.Influence of pitching motion on subsonic wing rock of slender delta wings[J].Journal of Aircraft,1989,26(6):503-508.

[17] Elzedbda J M,Nayfeh A H,Mook D T.Development of an analytical model of wing rock for slender delta wings[J].Journal of Aircraft,1989,26(8):737-743.

[18] Nayfeh A H,Elzedbda J M,Mook D T.Analytical study of the subsonic wing-rock phenomenon for slender delta wings[J].Journal of Aircraft,1989,26(9):805-809.

[19] Konstadinopoulos P,Mook D T,Nayfeh A H.Subsonic wing rock of slender delta wings[J].Journal of Aircraft,1985,22(3):223-228.

[20] Elzebda J M,Mook D T,Nayfeh A H.The influence of an additional degree of freedom on subsonic wing rock of slender delta wings[C]//25th Aerospace Sciences Meeting,Reston:AIAA,1987.

[21] Go T H,Ramnath R V.Analysis of the two-degree-offreedom wing rock in advanced aircraft[J].Journal of Guidance,Control,and Dynamics,2002,25(2):324-333.

[22] Ross A J.Investigation of nonlinear motion experienced on a slender-wing research[J].Journal of Aircraft,1972,9(9):625-631.

[23] Go T H,Ramnath R V.An analytical approach to the aircraft wing rock dynamics,AIAA-2001-4426[R].Reston:AIAA,2001.

[24] Jahnke C C,Culick F E C.Application of dynamical systems theory to the high angle of attack dynamics of the F-14,AIAA-90-0221[R].Reston:AIAA,1990.

[25] Liebst B S,Nolan R C.A simplified wing rock prediction method,AIAA-93-3662-CP[R].Reston:AIAA,1993.

[26] Nho K,Agarwal R K.Application of fuzzy logic to wing rock motion control,AIAA-98-0497[R].Reston:AIAA,1998.

[27] Tewari A.Nonlinear optimal control of wing rock including yawing motion,AIAA-2000-4251[R].Reston:AIAA,2000.

[28] Joshi S V,Sreenatha A G,Chandrasekhar J.Suppression of wing rock of slender delta wings using a single neuron controller[J].IEEE Transactions on Control Systems Technology,1998,6(5):671-677.

[29] Shue S P,Agarwal R K.Nonlinear H∞method for control of wing rock motions[J].Journal of Guidance,Control,and Dynamics,2000,23(1):60-68.

[30] Cao C Y,Hovakimyan N.Application of L1adaptive controller to wing rock,AIAA-2006-6426[R].Reston:AIAA,2006.

[31] Pietrucha J,Zlocka M,Sibilski K,et al.Comparative analysis of wing rock control,AIAA-2009-56[R].Reston:AIAA,2009.

[32] Liebst B S,Witt B R D.Wing rock suppression in the F-15 aircraft,AIAA-97-3719[R].Reston:AIAA,1997.

[33] Garrard W L,Jordan J M.Design of nonlinear automatic flight control systems[J].Automatica,1977,13(5):497-505.

[34] Montgomery R C,Moul M T.Analysis of deep-stall characteristic of T-tailed aircraft configuration and some recovery procedures[J].Journal of Aircraft,1966,3(6):562-566

[35] Powers B G.A Parametric study of factors influencing the deep-stall pitch-up characteristics of T-tail transport aircraft.NASA TN D-3370[R].Washington,D.C.:NASA,1966.

[36] Lee C S,Pang W W,Srigrarom S.Classification of aircraft by abnormal behavior of lift curves at low reynolds number,AIAA-2006-3179[R].Reston:AIAA,2006.

[37] Meznarsie V F,Gross L W.Experimental investigation of a wing with control midspan flow separation[J].Journal of Aircraft,1982,19(6):435-441.

[38] Gregory N,Quincey V G,Hall D J.Progress report on observation of three-dimensional flow patterns obtained during stall development on aerofoils and on the problem of measuring two-dimensional characteristics,NPL Aero Report-1309[R].Middlesex:NPL,1970.

[39] Mehra R K,Carroll J V.Bifurcation analysis of aircraft high angle-of-attack flight dynamics,AIAA-1980-1599[R].Reston:AIAA,1980.

[40] Carroll J V,Mehra R K.Bifurcation analysis of nonlinear aircraft dynamics[J].Journal of Guidance,Control,and Dynamics,1982,5(5):529-536.

[41] Chen Y S,Liung A Y T.Bifucation and chaos in engineering[M].New York:Springer,1998:154-261.

[42] Sibilski K.Problems of manoeuvring at post-critical angels of attack continuation and bifurcation methods approach,AIAA-2003-0395[R].Reston:AIAA,2003.

[43] Liaw D C,Song C C.Analysis of longitudinal flight dynamics:a bifurcation-theoretic approach[J].Journal of Guidance,Control,and Dynamics,2012,24(1):109-116.

[44] Cochran J E J,Ho C S.Stability of aircraft motion in critical cases[J].Journal of Guidance,Control,and Dynamics,1983,6(4):272-279.

[45] Gates O B,Minka K.Note on a criterion for severity of roll-induced instability[J].Journal of the Aerospace Sciences,1959,26(5):287-290.

[46] Young J W,Schy A A,Johnson K G.Pseudo steady-state analysis of nonlinear aircraft maneuvers,NASA-TP-1758-C1[R].Washington,D.C.:NASA,1980.

[47] Thomas S,Bajpai G,Kwatny H,et al.Nonlinear dynamics,stability and bifurcation in aircraft:simulation and analysis tools,AIAA-2005-6428[R].Reston:AIAA,2005.

[48] Guicheteau P H.Bifurcations theory in flight dynamics an application to a real combat aircraft,ONERA-TAP-90-116[R].Sigle:INIST,1990.

[49] Avanzini G,Matteis G D.Bifurcation analysis of a highly augmented aircraft model[J].Journal of Guidance,Control,and Dynamics,1997,20(4):754-759.

[50] Marusak A,Pietrucha J,Sibilski K.Prediction of aircraft critical flight regimes using continuation and bifurcation methods,AIAA-2000-0976[R].Reston:AIAA,2000.

[51] Lina L J,Moul M T.A simulator study of T-tail aircraft in deep stall conditions,AIAA-1965-0781[R].Reston:AIAA,1965.

[52] Beh H,Bunt R V D,Fischer B.High angle of attack approach and landing control law design for the X-31A,AIAA-2002-0247[R].Reston:AIAA,2002.

[53] AtesogluÖ,Özgören M K.High-αflight maneuverability enhancement of a twin engine fighter-bomber aircraft for air combat superiority using thrust-vectoring control,AIAA-2006-6056[R].Reston:AIAA,2006.

[54] Jouannet C,Krus P.Modelling of high angle of attack aerodynamic state-space approach,AIAA-2006-3845[R].Reston:AIAA,2006.

[55] Forsythe J R,Strang W Z,Squires K D.Six degree of freedom computation of the f-15e entering a spin,AIAA-2006-858[R].Reston:AIAA,2006.

[56] Michal T,Babcock D,Oser M,et al.BCFD unstructured-grid predictions on the F-16 XL(CAWAPI)aircraft,AIAA-2007-679[R].Reston:AIAA,2007.

[57] Green B E.Computational prediction of nose-down control for the pre-production F/A-18E at high angle of attack[J].Journal of Aircraft,2008,45(5):1661-1668.

[58] Park M Y,Park H U,Park S H,et al.Computational investigation of asymmetric vortical flow characteristics at high angle of attack,AIAA-2007-6727[R].Reston:AIAA,2007.

[59] Roberts L T,Strom T H.All-axis control of aircraft in deep stall:United States Patent,US 4099687[P].1978-07-11.

[60] Goman M,Fedulova E,Khramtsovsky A V.Maximum stability region design for unstable aircraft with control constrains,AIAA-1996-3910[R].Reston:AIAA,1996.

[61] Lowenberg M H.Bifucation analysis as a tool for post-departure stability enhancement,AIAA-1997-3716[R].Reston:AIAA,1997.

[62] Littleboy D M,Smith P R.Using bifurcation method to aid nonlinear dynamic inversion control law design[J].Journal of Guidance,Control,and Dynamics,1998,21(4):632-638.

[63] Gao H,Wang Z G,Zhang S G.A study of wing rock[J].Flight Dynamics,1989(3):1-10(in Chinese).高浩,王忠俊,张曙光.机翼摇晃运动研究[J].飞行力学,1989(3):1-10.

[64] Chen Y L,Shen H L,Liu C.Prediction and suppression of wing-rock[J].Acta Aeronautica et Astronautica Sinica,2005,26(3):276-280(in Chinese).陈永亮,沈宏良,刘昶.机翼摇晃预测与抑制[J].航空学报,2005,26(3):276-280.

[65] Zhou Y X,Liu C,Yin J H.The simulation study of deepstall characteristics for RSSairplane[J].Flight Dynamics,1996,14(4):19-24(in Chinese).周欲晓,刘昶,尹江辉.RSS飞机深失速仿真研究[J].飞行力学,1996,14(4):19-24.

[66] Yu Y J,Yin J H,Liu C.Analysis of deep stall corridor characteristics for RSS aircraft[J].Flight Dynamics,1998,16(2):1-6(in Chinese).余勇军,尹江辉,刘昶.RSS飞机深失速走廊特性分析[J].飞行力学,1998,16(2):1-6.

[67] Zheng X F,Liu C,Shi Z W.Study of deep-stall characteristics of T-tailed aircraft[J].Flight Dynamics,1996,14(3):39-43(in Chinese).郑贤芬,刘昶,史志伟.“T”型尾翼飞机的深失速特性研究[J].飞行力学,1996,14(3):39-43.

[68] Cheng Z Y.Analysis of stall behavior for Y7-200Baircraft[J].Flight Dynamics,1993,11(2):64-72(in Chinese).程泽荫.Y7-200B飞机失速特性分析[J].飞行力学,1993,11(2):64-72.

[69] Cheng Z Y.The study of control and stability characteristics for Y7-200B/A aircraft[J].Flight Dynamics,1995,13(4):56-64(in Chinese).程泽荫.Y7-200B/A飞机操稳特性分析[J].飞行力学,1995,13(4):56-64.

[70] Wang D H,Su B,Wang Z G.Analysis of global stability and nonlinear control for a fighter configuration[J].Acta Aerodynamica Sinica,2002,20(2):192-197(in Chinese).王大海,苏彬,王忠俊.飞机的全局稳定性分析和非线性控制[J].空气动力学学报,2002,20(2):192-197.

[71] Li K,Fang Z P.High angle-of-attack control law design based on global stability analysis[J].Journal of Beijing University of Aeronautics and Astronautics,2004,30(6):516-519(in Chinese).黎康,方振平.基于全局稳定性分析的大迎角飞控系统设计[J].北京航空航天大学学报,2004,30(6):516-519.

[72] Li K,Fang Z P.Application of bifurcation analysis to aircraft nonlinear dynamics[J].Flight Dynamics,2003,21(4):5-8(in Chinese).黎康,方振平.分叉分析在飞机非线性动力学中的应用[J].飞行力学,2003,21(4):5-8.

[73] Zanotti A,Nilifard R,Gibertini G,et al.Assessment of 2D/3D numerical modeling for deep dynamic stall experiments[J].Journal of Fluids and Structures,2014,51:97-115.

[74] Wang S Y,Ingham D B,Ma L,et al.Turbulence modeling of deep dynamic stall at relatively low Reynolds number[J].Journal of Fluids and Structures,2012,33:191-209.

[75] Visbal M R.Numerical investigation of deep dynamic stall of a plunging airfoil[J].AIAA Journal,2011,49(10):2152-2170

[76] Shi Z K,Fan L.Bifurcation analysis of polynomial models for longitudinal motion at high angle of attack[J].Chinese Journal of Aeronautics,2013,26(1):151-160.

[77] Fan L,Shi Z K.Stability and bifurcation analysis of nonlinear model for longitudinal motion with time delay[J].Control and Decision,2013,28(7):985-990(in Chinese).范丽,史忠科.具有时滞的非线性纵向飞行模型稳定性和分支分析[J].控制与决策,2013,28(7):985-990.

[78] Xin Q,Shi Z K.Bifurcation analysis and stability design for aircraft longitudinal motion with high angle of attack[J].Chinese Journal of Aeronautics,2015,28(1):250-259.

[79] Shi Z K,Wu F X.Robust identification method for nonlinear model structures and its application to high-performance aircraft[J].International Journal of Systems Science,2013,44(6):1040-1051.

[80] Zhang H Y,Shi Z K.Variable structure control of catastrophic course in airdropping heavy cargo[J].Chinese Journal of Aeronautics,2009,22(5):520-527.

[81] Chen J,Shi Z K Aircraft modeling and simulation with cargo moving inside[J].Chinese Journal of Aeronautics,2009,22(2):191-197.

[82] Chen J,Shi Z K.Flight controller design of transport airdrop[J].Chinese Journal of Aeronautics,2011,24(5):600-606.

[83] Feng Y L,Shi Z K,Tang W.Dynamics modeling and control of large transport aircraft in heavy cargo extraction[J].Journal of Control Theory and Applications,2011,9(2):231-236.

[84] Xin Q,Shi Z K.Design of three dimensional nonlinear controller for transport aircraft airdropping heavy cargoes at extremely low-altitude under cross wind[J].Acta Aeronautica et Astronautica Sinica,2014,35(7):1941-1956(in Chinese).辛琪,史忠科.运输机超低空重装空投抗侧风三维非线性控制律设计[J].航空学报,2014,35(7):1941-1956.

[85] Hancock G J.Theory of optimum aerodynamic shapes[J].Nature,1966,102(5031):53-54.

[86] Gruschka H D,Borchers I U,Coble J G.Aerodynamic noise produced by a gliding owl[J].Nature,1971,233(5319):409-411.

[87] Christopher J.C.Aerodynamic properties of insert wing section and a smooth aerofoil compared[J].Nature,1975,258(13):141-142.

[88] Dickinson M H,Lehmann F O,Sane S P.Wing rotation and the aerodynamic basis of insect flight[J].Science,1999,284(5422):1954-1960.

[89] Fry S N,Sayaman R,Dickinson M H.The aerodynamics of free-flight maneuvers in drosophila[J].Science,2003,300(5618):495-498.

[90] Dial K P.Wing-assisted incline running and the evolution of flight[J].Science,2003,299(5605):402-404.

[91] Muijres F T.Leading-edge vortex improves lift in slowflying bats[J].Science,2008,319(5867):1250-1253.

[92] Papatheou E,Manson G,Barthorpe R J,et al.The use of pseudo-faults for damage location in SHM:An experimental investigation on a piper tomahawk aircraft wing[J].Journal of Sound and Vibration,2014,333(3):971-990.

[93] Lee S,Park W,Jung S.Fault detection of aircraft system with random forest algorithm and similarity measure[J].The Scientific World Journal,2014.DOI:http://dx.doi.org/10.1155/2014/727359(in Press).

[94] Martinez A,Sanchez L,Couso I.Interval-valued blind source separation applied to ai-based prognostic fault detection of aircraft engines[J].Journal of Multiple-Valued Logic and Soft Computing,2014,22(1-2):151-166.

[95] Liu X,Liu Z.A hybrid approach for aircraft fault diagnosis based on fault inference and fault identification[J].Aeronautical Journal,2014,118(1199):81-97.

[96] Nayebpanah N,Rodrigues L,Zhang Y M.Fault tolerant control for partial loss of control authority in aircraft using piecewise affine slab models[J].Journal of the Franklin Institute-Engineering and Applied Mathematics,2013,350(9):2494-2508.

[97] Loza A F D,Cieslak J,Henry D,et al.Sensor fault diagnosis using a non-homogeneous high-order sliding mode observer with application to a transport aircraft[J].IET Control Theory and Applications,2015,9(4SI):598-607.

[98] Yaramasu A,Cao Y N,Liu G J,et al.Aircraft electric system intermittent arc fault detection and location[J].IEEE Transactions on Aerospace and Electronic Systems,2015,51(1):40-51.

[99] Shi Z K.Aircraft fault diagnosis and tolerant control based on three-dimensional motion model,China,ZL201310095792.0[P].2015-04-08(in Chinese).史忠科.飞行器三维运动故障诊断和容错控制方法,中国:ZL201310095792.0[P].2015-04-08.

[100]Madany Y M,Elkamchouchi H M,Ahmed M M.Modelling and simulation of robust navigation for unmanned air systems(UASs)based on integration of multiple sensors fusion architecture[C]//UKSim-AMSS 7th European Modelling Symposium on Computer Modelling and Simulation,2013:719-724.

[101]Xu Y,Sun W,Li P.A Miniature integrated navigation system for rotary-wing unmanned aerial vehicles[J].International Journal of Aerospace Engineering,2014:748940.

[102]Figueiroa M,Moutinho A,Azinheira J R,et al.Attitude estimation in SO(3):a comparative UAV case study[C]//IEEE International Conference on Autonomous Robot Systems and Competitions.Piscataway,NJ:IEEE Press,2014:79-84.

[103]Grelsson B,Felsberg M.Probabilistic hough voting for attitude estimation from aerial fisheye images[J].Lecture Notes in Computer Science,2013:478-488.

[104]Yigit H,Yilmaz G.Development of a GPU accelerated terrain referenced UAV localization and navigation algorithm[J].Journal of Intelligent&Robotic Systems,2013,70(1-4):477-489.

[105]Chee K Y,Zhong Z W.Control,navigation and collision avoidance for an unmanned aerial vehicle[J].Sensors and Actuators A:Physical,2013,190(1):66-76.

[106]Zhang L,Shi Z,Zhong Y.Attitude estimation of 3-DOF lab helicopter based on optical flow[C]//33rd Chinese Control Conference,2014:8536-8541.

[107]Zsedrovits T,Bauer P,Zarandy A,et al.Error analysis of algorithms for camera rotation calculation in GPS/IMU/camera fusion for UAV sense and avoid systems[C]//International Conference on Unmanned Aircraft Systems,2014:864-875.

[108]Ding Y R,Hsiao F B.Application of a single-antenna gpsbased attitude estimation on the stability control of a small unmanned aerial vehicle[J].Journal of Aerospace Engineering,2013,26(4):768-785.

[109]Marinho M A M,Ferreira R S J,Costa J P C L D,et al.Antenna array based positioning scheme for unmanned aerial vehicles[C]//17th International ITG Workshop on Smart Antennas,2013:1-6.

[110]Liu K,Da Costa J P C L D,So H C,et al.3-D unitary ESPRIT:Accurate attitude estimation for unmanned aerial vehicles with a hexagon-shaped ESPAR array[J].Digital Signal Processing,2013,23(3):701-711.