基于匹配渐进展开的跳跃式再入解析预测-校正制导律设计

崔乃刚*,黄荣傅瑜,韩鹏鑫

1.哈尔滨工业大学 航天学院,哈尔滨 150001 2.北京宇航系统工程研究所,北京 100076 3.中国运载火箭技术研究院 研究发展中心,北京 100076

随着中国探月工程的逐步深入,2014年10月,探月工程三期再入返回飞行试验的返回器采用半弹道跳跃式再入返回技术,成功返回并着陆在内蒙古四子王旗回收区[1]。选择内陆地区为着陆区主要是因为目前中国还不能全球布站,测控能力有限,且着陆场的约束较强,因此要求探月飞船必须具有较大的航程能力。对于低升阻比返回舱(例如:神舟飞船和嫦娥卫星),要想执行长航程再入返回飞行任务,最好的方法就是采用跳跃式再入技术,即探测器在进入大气层后依靠气动力再次跃出大气层飞行一段时间后,第2次再入大气层并最终着陆[2]。由于再入返回过程速度大、航程长、高动态、姿态与弹道耦合强烈,这就要求飞行制导系统必须能够提供快速、精确的跳跃再入制导指令。

大气跳跃再入轨迹最初是为阿波罗登月任务设计的[3],现在再次考虑将其用于类似的低升阻比飞行器[4]。一个跳跃再入轨迹起始于再入点,具有较大的再入速度(近似第二宇宙速度)和较小的飞行路径角。进入大气层后,气动升力连续调整飞行速度矢量直至飞行器跳出稠密大气层。跳出大气层以后,飞行器进行开普勒飞行直至再次进入大气层。本文主要是通过规划大气跳出点的速度和飞行路径角来控制飞行器的总航程。

再入过程中的倾侧角是唯一控制变量,它通过绕速度矢量旋转飞行器以改变气动升力的垂直分量[5]。阿波罗再入制导系统采用闭环轨迹解预测跳出点速度和路径角,使用的方程为非线性运动方程的简化近似。总航程通过拼接初始大气跳跃段、开普勒段和再次进入大气段的估计航程获得,当预测航程等于剩余航程时再调整倾侧角。

尽管事实证明了阿波罗再入制导方法的成功性,但其航程预测能力有限(最大为4 630 km,对应41°航程角)[6]。针对新型低升阻比飞行器的设计目标(包括扩展、中止和其他意外情况下的航程能力),Bairstow[7]、Brunner和Lu[8]开发了数值积分预测制导方法,通过数值积分使整个非线性运动方程组向前推进跳跃轨迹,并通过迭代方式对倾侧角进行调整直至预测航程等于剩余航程。文献[9]中的预测校正制导律分别成功获得了10 006.2 km(90°航程角)和79 679 km(72°航程角)的航程,但其计算量相对较大,对机载计算机提出了较高的要求。

本文基于匹配渐进展开法[10-13],提出了一种解析预测-校正再入制导方法。根据跳跃再入飞行过程中不同阶段飞行器的受力情况不同,该方法将运动方程的解分为以重力作用为主导的外解和以气动力作用为主导的内解,采用匹配渐进展开法获得统一的封闭解析表达式。通过解析解不断预测剩余航程,通过落点偏差不断迭代修正升阻比垂直分量和倾侧角指令,最终获得满足射程要求和落点精度的大气跳跃再入轨迹。

1 跳跃再入运动模型

1.1 运动方程

质点飞行器在地心惯性坐标系下的平面运动方程[14]为

式中:r为飞行器到地球中心的距离；t、V 和γ分别为飞行器的飞行时间、飞行速度和飞行路径角(沿当地水平面向上为正)；ρ为大气密度；CL和CD分别为升力系数和阻力系数；S为特征面积；m为飞行器质量；μ为中心天体的引力系数。同时,假设大气密度为指数形式,即

式中:H=7.9 km为密度模型的匀质大气高度值；rref为参考半径,取高度为61.8 km(跳跃机动的拉起高度附近)处的地心矢径值。参考半径处的大气密度ρ(rref)取为2.467×10-4kg/m3。若飞行器在大气层外飞行时,大气密度为零,则式(1)表示开普勒运动。

为了获得近似解析解,式(1)被转变为以高度为自变量的2个方程,并引入以下无量纲化过程:

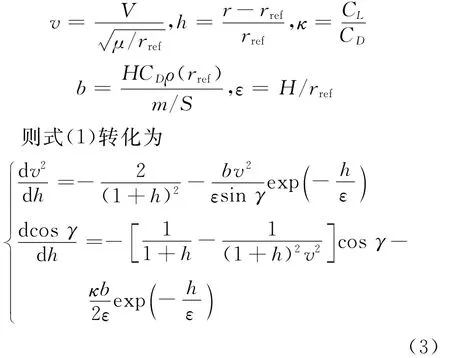
1.2 跳跃再入轨迹

类似阿波罗再入制导,大气跳跃段轨迹规划是制导律设计的基础。图1为纵程约为8 338.5 km的跳跃再入轨迹各个制导阶段的示意图,共包括下降段、上升段、开普勒段和末段4个阶段。从图1中可以看出,下降段为从再入点(Entry Interface,EI)处到跳跃再入最小高度处(飞行路径角γ=0°),上升段为从最小高度处到跃出大气处(在第2次再入大气前为开普勒段),末段为从二次大气再入到开伞着陆。注意到,开普勒段的高度边界并非必须在EI上,而是在某个阻力加速度充分小的高度上(如阿波罗制导中定义“跃出”在阻力加速度小于0.2g时的点上)。由于高度为匹配渐进展开法中的自变量,所以它是开普勒段开始的“触发器”。对于纵程小于4 632 km的情况,开普勒段的开始高度可以定在65 km；对于纵程大于4 632 km的跳跃轨迹,开普勒段的开始高度可以定在85 km。采用较大的跃出高度时,大气阻力的影响会随之变小,从而能够提高大航程跳跃轨迹预测精度。

图1 跳跃再入飞行轨迹剖面及制导分段Fig.1 Trajectory profile and guidance section of skip entry flight

2 基于匹配渐进展开的解析跳跃轨迹

跳跃轨迹起始于重力为主的区域(外部区域),然后进入空气动力为主的区域(内部区域),最后再到达重力为主的区域。参考式(3),2个等式等号右边的第1项表示重力起主要作用,第2项表示空气动力起主要作用。直接获得式(3)解析解的困难之处在于没有2个区域都适合的易于获得的解析解的近似形式,而解决此困难的一种方式为先在每个区域获得独立的解(外部区域对应的解称为外解,内部区域对应的解称为内解),然后再将其匹配融合成统一的形式(统一解)。匹配渐进展开法为一种奇异摄动技术[15-16],可实现此目标。

2.1 外解与内解的渐进展开

高度h和高度比ε的数值决定了跳跃轨迹上的某个特定点是在内部区域还是外部区域。当h相对于ε很大时,式(3)中的空气动力项趋于零,此时的运动轨迹可近似为开普勒轨道。因此在外部区域,空气动力项的影响被看作小阶扰动。而当h和ε相当时,空气动力项不能再被看作是小量,并且可认为空气动力远大于重力,此时的运动轨迹无法被近似为开普勒轨道。因此在内部区域内,会将重力项作为一个低阶的摄动项。

匹配渐进展开法的一个关键特征为不同区域的近似方程来自于对同一方程组的限制处理,并且此限制过程都需要小量趋于零。因此在内区域,将式(3)表示成扩展变量的形式:

式中:vi和γi(i=0,1,2,…)分别为速度和飞行路径角关于高度h的第i阶展开项。

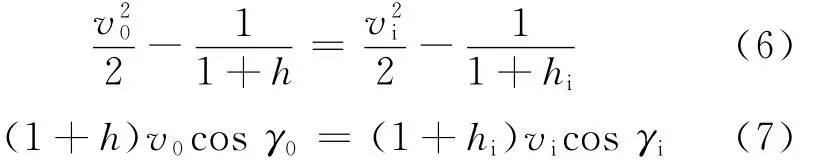
式中:hi、vi和γi分别为高度、速度和飞行路径角在外部区域的初始条件。定义速度和飞行路径角的复合常值为

因此,式(4)和式(5)的首项即为精确的外部解。实际上,式(6)和式(7)为开普勒运动积分,分别表示能量守恒和角动量守恒。

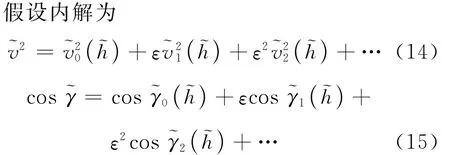
式中:～表示内解对应的相应变量。

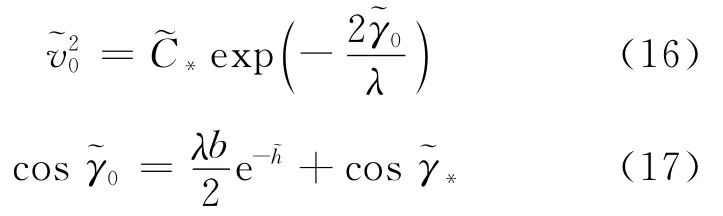
式中:λ=(CL/CD)cosσ为升阻比的竖直分量,σ为倾侧角和为积分常数,并与内部区域高度、速度和飞行路径角的初始 条 件()有关,即

由式(18)和式(19)可知,高阶项似乎不能以闭环形式获得。文献[10]中以积分形式给出了一阶解,但本文只考虑首项。

2.2 外解与内解的匹配

在获得外解和内解的首项以后,开始构造统一有效解的首项。合成解通过将外解和内解相加后再减去它们的公共部分获得,这样得到的合成解将包含4个未知常 数 (v*,cosγ*,cos)。根据已知初始条件(hi,v(hi),γ(hi))只能解算出其中2个常数,因此还需要增加另外2个边界条件,可以通过在重叠区域对外解和内解进行匹配获得相应的边界条件。当前情况下,匹配意味着外解对小的高度h和内解对大的扩展高度h~之间的协调。

通过匹配外解和内解的首项,可得到

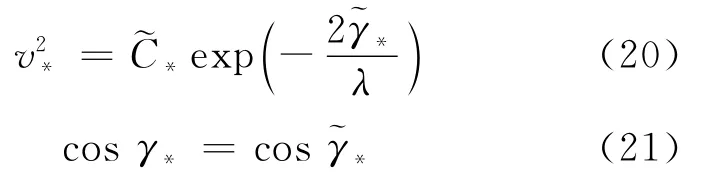
式(20)和式(21)的等号左边表示当h→0时对外解的限制,等号右边表示当扩展高度h~→∞时对内解的限制。从而得到一致有效合成解为

此解近似于式(3)的统一解。

2.3 跳跃段解析解计算流程

为了进一步的研究,考虑在给定初始条件(hi,v(hi),γ(hi))(即再入大气前轨迹上的一点,并在外区域)的情况下,如何通过式(22)和式(23)获得近似跳跃轨迹。

根据假设,可在初始点忽略空气力,故常数v*和cosγ*的值可以通过式(8)和式(9)计算得出,常数cos~γ*可以通过式(21)计算得出。在此基础上,结合式(22)和式(23)可计算出v和γ的值。但是,如果实际轨迹为跳跃的,那么初始为负的飞行路径角γ会随着高度h的减小而增加,并且在高度降至最低hmin时为零。那么,存在的问题是内解(实际上是cos)可能比合成解γ先变成零,因为它们的ε阶项不同。此时,在γ=0°附近可能会出现cos＞1的情况。为了避免这种情况的发生,不应再使用式(21)来计算~γ*,而应该通过式(25)对其进行求解[17]。

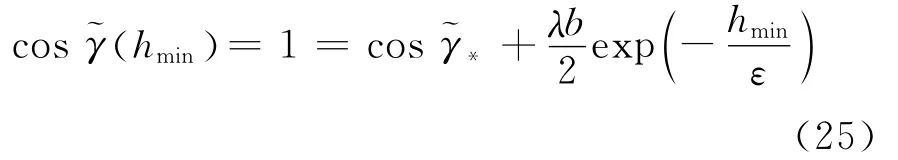
在计算得到v*和cosγ*后,再通过式(23)进行迭代即可确定最小高度hmin。由这种方式获得的值将导致式(21)左右两边的ε阶项不一致。但这是允许的,因为匹配只要求阶一致。

在最小高度hmin处(此高度将跳跃轨迹的下降段γ＜0°和跳出段γ＞0°分开),需要对常数(v*,cosγ*,cos)进行调整,这是由于v和γ为关于h的双值函数。由于飞行路径角在跳出阶段为正,导致(当h→∞时内解的极限)也应为正。更确切地说,由内解关于最小高度hmin的对称性表明:

式中:(·)exit和(·)entry分别表示跃出段和再入段的相关变量。

现在整条跳跃轨道的近似已经完成了。式(22)和式(23)的合成解为近似的基础,式(8)、式(9)以及式(25)～式(28)用于计算常数。需要注意的是,通过式(8)和式(9)计算v*和γ*时,需要给出的初始条件是在外区域。如果给出的初始条件沿着再入段轨迹离再入点比较远(空气动力不能忽略),那么需要同时解算式(22)、式(23)和式(25)以计算再入常数v*、γ*和。同样的,跳出段情况也是如此。

考虑再入段常数v*和γ*。由式(8)和式(9)可知,v*和γ*与大气层外的某点状态(v(hi),γ(hi))有关,并且再入段的飞行路径角γ*应为负。将式(8)和式(9)重写成开普勒转移轨道的能量和角动量积分的形式,即

因此,v*和γ*的物理意义分别为再入段在h=0 km(即参考半径rref)处的飞行器速度和飞行路径角。当然,只有忽略飞行过程中的空气动力,才能够保证获得此物理意义。这是由于可能存在cosγ*＞1的情况,而这本身在数学上并不矛盾,因为cosγ*是包括初始条件式(9)的合成解的任意标注。但是,如果使用式(21)确定cos~γ*,那么矛盾就会产生,因为需要计算cos~γ*的反余弦。正如2.3节所建议的,通过式(25)计算~γ*,不仅能避免一个难题,也能避免此数学矛盾。另一个补救措施为增加rref的值。但是,如果rref过大,位于rref半径圆附近的ε阶的边界层将不再是气动力为主。这是由于为满足cosγ*＜1,rref将取大气层内相对较高的一个值。那么当h为ε阶时,空气动力为主的假设将不再成立。轨道衰减最好使用规则摄动,并通过非奇异摄动进行近似。对于一阶近似,规则摄动理论下的轨迹仅由重力决定,而空气动力被当作小的摄动项,即只存在一个外区域。总之,对于再入之前的某点,当初始条件不严格要求满足cosγ*＜1时,表明该点在匹配渐进展开获得的近似解的适用区域附近。

类似的,对于跳跃段的常数(v*)exit和(cosγ*)exit来说,其物理意义分别为不考虑空气动力时,飞行器在r=rref或h=0 km时的速度和飞行路径角。

一旦通过式(8)和式(9)以及初始状态确定了常值v*和γ*,便可以应用条件cosγ=1,通过式(23)确定跳跃轨迹最小高度。因为式(23)是关于h的超越方程,故可采用牛顿迭代法确定hmin。庆幸的是,式(23)关于h的解析导数可以获得,牛顿迭代法在迭代4～5次后即可收敛。

3 跳跃再入轨迹制导策略

3.1 纵向航程预测

本文提出的跳跃制导通过对升阻比垂向分量λ进行迭代,使预测总航程匹配到达目标落点的需要航程。在再入的初始点,λ取一个标称试用值,通过式(22)和式(23)解析地计算出一条大气跳跃轨迹(实际上,迭代得到的就是一条参考轨迹)。

预测总航程表示为

式中:Rdown、Rup、RKepler和Rfinal分别为下降段、上升段、开普勒段和末段的航程。跳跃再入上升段和下降段的航程角θ通过积分航程角对速度的微分来确定。

dθ/d V的离散值可通过求解在再入点处高度hEI和hmin(下降段)以及hmin和跃出高度hexit(上升段)之间的解析跳跃解(式(22)和式(23))来计算得到,并采用梯度积分法对dθ/d V 进行积分；然后,各段纵程可用地球半径rE乘以航程角来计算得到,例如:Rdown=rEθdown,Rup=rEθup(θdown和θup分别为下降段和上升段的航程角)。

开普勒段的航程角可通过二体假设运动进行计算:

式中:γexit为预测的跃出飞行路径角；P = (Vexit/)2,Vexit为预测的跃出速度,Vecixrict=为当地圆轨速度,rexit为跃出时飞行器到地球中心的距离。跃出速度Vexit和飞行路径角γexit将由匹配渐进展开解式(22)和式(23)在跃出高度hexit处计算得到。

末段纵程Rfinal通过对存储的参考轨迹进行线性内插来计算得到。这里采用了阿波罗制导的标准末段剖面,此时的常值升阻比垂向分量为λfinal=0.18(σ=53°)。标准参考轨迹采用速度作为自变量,由于假定在二次再入时的速度等于跃出大气时的速度,因此有Rfinal=f(Vexit)。

实际的需要航程Rgo通过飞行器的当前位置向量和目标落点区的位置向量来计算得到。升阻比垂向分量λ采用正割迭代法调整,直到预测纵程偏差|Rtotal-Rgo|＜46.3 km(约25 n mile)。迭代程序运行2次:第1次是在再入点EI处,第2次是在最小高度hmin处。在hmin处重新计算跳跃轨迹的剩余上升段极大地提高了对大气跃出状态Vexit和γexit的预测,因为匹配渐进展开解的复合常值v*、γ*和~γ*能通过采用飞行器最低点当前状态重新计算。数值仿真结果表明,在所有尝试情况下,λ在3～5次迭代后收敛(阿波罗制导也采用了总迭代次数限制在7次之内的正割迭代法)。

3.2 倾侧角指令生成

由解析航程预测迭代得到的升阻比垂向分量λ的开环值可通过采用阿波罗反馈策略的闭环项进行扩展[18]。

在下降段和上升段,指令升阻比垂向分量为

式中:常值λref为航程预测迭代得到的结果；Vref和˙rref分别为参考速度和参考高度变化率,可通过式(22)和式(23)的当前高度函数形式的封闭解来计算得出；参考阿波罗的制导增益形式,速度增益KV与当前阻力加速度aD成比例:

（3）研制钢筋笼自动绑扎或焊接智能设备。可按照导入的CAD网片规格进行全过程自动生产的智能设备；焊接或者绑扎的钢筋直径范围广，质量可靠；钢筋网络尺寸精确要高，在±10mm范围内；可根据预埋件、窗户、门口尺寸，自动按照预留尺寸开孔；具有互联网和通信接口，可方便技术人员通过互联网远程诊断/故障排除。

其中:aexitD=1.22 m/s2为跃出高度附近的近似阻力加速度；ahminD为在上拉高度处的估计阻力加速度。高度变化率增益KRD为

在开普勒段,采用常值倾侧角飞行,这里取λ=0.250 3(相应的σ=33.44°)。

在末段(二次再入段),基于线性摄动理论和存储的参考轨迹,指令升阻比垂向分量为

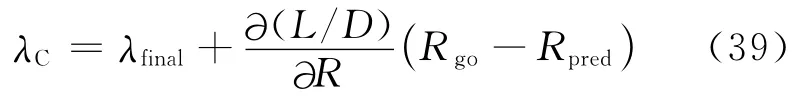
式中:L为升力；D为阻力；R为航程；Rpred为预测剩余航程,并有

其中:arefD为阻力加速度的参考值。

该段所有的参考值都将通过线性内插已存储的以速度为自变量的参考剖面来进行计算；偏导数将通过伴随法和一个线性化系统来计算,并且存储为速度的函数。阿波罗飞船返回舱的最终段制导参考轨迹参数如表1所示。

表1 阿波罗飞船返回舱最终段制导参考轨迹参数Table 1 Reference trajectory parameters of terminal guidance for Apollo entry capsule

式中:(L/D)max=0.3,表示最大升阻比。这里采用了阿波罗侧向制导逻辑,如果横程偏差超过了

最后得到倾侧角为某一边界值,则进行指令倾侧翻转,其中,边界值的界限与V2成比例,以限制翻转次数。

4 仿真分析

4.1 仿真初值

以阿波罗指令舱[3](Command Module,CM)为对象进行制导算法的验证,其参考面积为S=11.9 m2,质量为m=5 511 kg,配平攻角αT的范围为147°～158°。升力系数和阻力系数可通过以马赫数Ma为自变量对配平气动系数线性插值得到。表2为阿波罗飞船返回舱升阻比与配平攻角的关系,表3为数值仿真再入点的初始参数。期望的落点经度为75°,相应的航程为8 348.959 19 km,对落点纬度不进行要求。

表2 阿波罗返回舱升阻比L/D与配平攻角αT的关系Table 2 Relationship between lift-drag ratio L/D and trim angle of attackαT for Apollo entry capsule

表3 再入点(EI)初始参数Table 3 Initial parameters of entry interface(EI)

4.2 计算结果

仿真得到的阿波罗指令舱再入制导的落点参数如表4所示,相应的航程为8 348.620 90 km,落点误差为0.338 29 km。整个再入过程的高度和倾侧角变化如图2所示。

表4 再入制导落点参数Table 4 Landing parameters of entry guidance

图2 跳跃再入制导轨迹中的飞行高度和倾侧角变化曲线Fig.2 Flight altitude and bank angle variation curves of skip entry guidance trajectory

从图2中可以看出,本文所给出的载人飞船返回舱再入制导算法可以很好地实现跳跃式再入,航程达到了8 348.62 km,且具有较高精度。图2(b)中的倾侧角变化曲线不连续光滑,主要是因为倾侧角指令是分段进行设计的,而段间的衔接问题没有考虑,这一问题将在后续的研究中进行解决。

5 结 论

1)采用跳跃式再入返回形式,将阿波罗指令舱的再入航程由4 630 km提高到8 348 km,满足了低升阻比飞行器再入返回的大航程要求。

2)利用奇异摄动技术中的匹配渐进展开法,获得了跳跃式再入返回轨迹的统一封闭解析解——飞行速度和飞行路径角关于高度和初始条件的解析表达式,并给出了具体的计算流程和注意事项,验证了匹配渐进展开技术求解变系数、非线性问题的有效性。

3)预测-校正制导律对大航程再入返回过程中剧烈的环境变化具有较强的鲁棒性,而基于解析解的航程预测保证了制导的快速性,而制导指令(倾侧角)的生成不仅考虑了航程偏差,还加入了高度、速度和加速度偏差的补偿,仿真结果证明了该解析预测-校正制导的有效性和高精度。

[1] Li S H,Pang D.Six key technologies of“returning home”safely[N].China Aviation News,2014-11-01(003)(in Chinese).李淑姮,庞丹.安全“回家”之六大关键技术[N].中国航天报,2014-11-01(003).

[2] Du X,Li H Y.Design of skip entry guidance for lunar-return vehicle[C]//Proceedings of Collection of the Eighth Academic Conference of Chinese Society of Astronautics Space Exploration Technology Committee.Beijing:Chinese Society of Astronautics,2011:33-36(in Chinese).杜昕,李海阳.探月飞船跳跃式再入制导律设计[C]//中国宇航学会深空探测技术专业委员会第八届学术年会论文集.北京:中国宇航学会,2011:33-36.

[3] Graves C A,Harpold J C.Apollo experience report—mission planning for Apollo entry,NASA TN D-6725[R].Washington,D.C.:NASA,1972.

[4] Lu P.Predictor-corrector entry guidance for low lifting vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1067-1075.

[5] Kluever C A.Entry guidance using analytical atmospheric skip trajectories[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1531-1534.

[6] Morth R.Reentry guidance for Apollo,MIT Instrumentation Lab Report R-532[R].Cambridge,MA:Massachusetts Institute of Technology,1966.

[7] Bairstow S H.Reentry guidance with extended range capability for low L/D spacecraft[D].Cambridge,MA:Massachusetts Institute of Technology,2006.

[8] Brunner C W,Lu P.Skip entry trajectory planning and guidance,AIAA-2007-6777[R].Reston:AIAA,2007.

[9] Lu P.Predictor-corrector entry guidance for law-lifting vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1067-1075.

[10] Shi Y Y,Pottsepp L.Asymptotic expansion of a hypervelocity atmospheric entry problem[J].AIAA Journal,1969,7(2):353-355.

[11] Shi Y Y,Pottsepp L,Eckstein M C.A matched asymptotic solution for skipping entry into planetary atmosphere[J].AIAA Journal,1971,9(4):736-738.

[12] Vinh N X,Busemann A,Culp R D.Hypersonic and planetary entry flight mechanics[M].Ann Arbor,MI:The University of Michigan Press,1980:254-272.

[13] Calise A J,Melamed N.Optimal guidance of aeroassisted transfer vehicles based on matched asymptotic expansions[J].Journal of Guidance,Control,and Dynamics,1995,18(4):709-717.

[14] Vinh N X.Optimal trajectories in atmospheric flight[M].New York:Elsevier Scientific,1981:58-60.

[15] Liu R C.Some methods for singular perturbation problems[D].Jilin:Jilin University,2008(in Chinese).刘日成.奇异摄动问题中的若干方法[D].吉林:吉林大学,2008.

[16] Xu B.Asymptotic analysis of solutions for some classes of singularly perturbed boundary value problems[D].Maanshan:Anhui University of Technology,2011(in Chinese).徐彪.几类奇摄动边值问题解的渐进分析[D].马鞍山:安徽工业大学,2011.

[17] Kuo Z,Vinh N X.Improved matched asymptotic solutions for three-dimensional atmospheric skip trajectories[J].Journal of Spacecraft and Rockets,1997,34(4):496-502.

[18] Moseley P E.The Apollo entry guidance:A review of the mathematical development and its operational characteristics,Rept.69-FMT-791[R].Houston:TX,1969.