摩擦加载式负载模拟器摩擦盘温度场研究

王尚东，李军

(哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001)

0 前言

负载模拟器是一种重要的半实物仿真设备，国内外有很多的专家学者对负载模拟器做了很多的研究工作，研制性能优良的负载模拟器具有重要的意义。由于一般负载模拟器会产生严重的多余力问题，一直以来专家学者从结构和控制算法上提出了很多抑制或消除多余力的方案，但是这些方法都不能很好地解决多余力问题。本文作者在前人理论的基础之上，以摩擦加载式的负载模拟器为研究对象，对系统中的发热问题进行仿真分析。这种摩擦加载式的负载模拟器，不仅消除了多余力对系统的影响，还大幅提高了系统的频宽。它的原理是利用液压缸推动摩擦片，从而产生摩擦力实现加载。通过改变液压缸内的油压大小，进而调节摩擦副之间的摩擦力大小。但是在摩擦加载过程中，会产生大量的热，生成的热量会对摩擦片的材料性能和加载性能产生较大影响。摩擦因数作为表征摩擦片性能最重要的参数，受温度影响很大。因此，如何准确建立接触工作面上温度场的数学模型，对摩擦片的材料选择以及性能分析具有重要的现实意义。基于热－结构耦合原理，建立摩擦盘温度场数学模型，为有限元仿真提供理论基础，并为确定液压控制参数、提高摩擦片使用寿命和材料优选提供一定的帮助。

1 温度场数学模型的建立

如图1所示，以空间中任一微元六面体为研究对象，各处的温度可以用位置和时间的函数式来表达，即:T=T(x，y，z，t)。

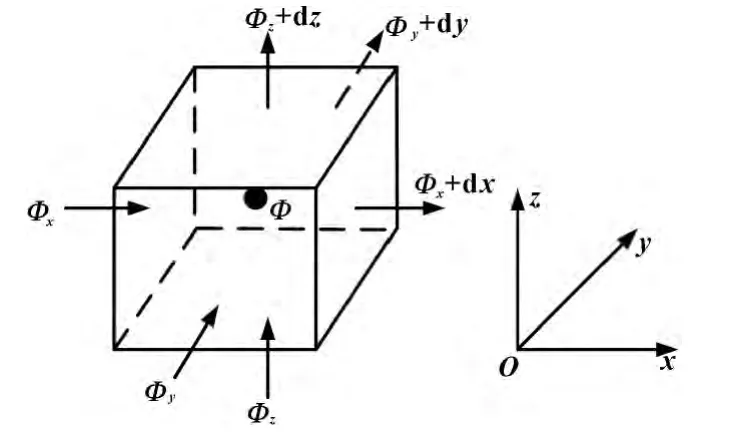
图1 微元体的三维热平衡分析

通过x=x，y=y，z=z3个微元表面导入微元体的热流量可写为

通过x=x+d x，y=y+d y，z=z+d z 3个表面，导出微元体的热流量亦可写出:

将式(1)—(4)代入能量守恒定律中，经整理得

式(6)中的T(x，y，z，t)正是要求的弹性体内温度场结果。通过有限元法或有限差分法，就可以求出摩擦盘上的温度场分布。

2 温度场的有限元仿真分析

2.1 模型建立

在ABAQUS中建立模型如图2所示。下部件为摩擦盘，绕z轴作旋转运动;上部件为摩擦片，固定不动。

图2 ABAQUS所建立的有限元模型

有限元模型的尺寸和相关参数见表1—3。

表1 有限元模型形状尺寸

表2 有限元模型中摩擦盘参数

表3 有限元模型中摩擦片参数

2.2 主要边界条件

(1)热交换系数

当空气流动雷诺数Re≤2.4×105时，热交换系数的经验公式可写为:式中:ka为空气的热传导系数;Dd为摩擦盘的外圆直径;Re为空气流动雷诺数，其表达式为:

在企业集团战略性成本建设中，应该将战略成本管理作为重点，通过战略管理工作的确定，进行战略活动的任务创新，展现活动工作创设的价值性，为现代企业的发展提供支持,而且，在案例管理活动构建中，其最终目标是通过公司优势的分析，进行战略成本管理工作的设计，为战略管理提供决策支持，为企业集团战略管理目标的强调提供支持，提高企业竞争的优势性。

式中:ω为角速度;ρa为空气密度;dd为摩擦盘的外圆直径;νa为空气黏度系数。其中，ka=0.027 6 W/(m·K)，ρa=1.13 kg/m3，νa=1.91×10－5kg/(m·s)，ca=1.005 kJ/(kg·K)。热交换系数表达式为:

(2)热流密度分配系数

摩擦盘/摩擦片之间的热流密度分配系数为:

式中:k为热传导系数，c为材料的比热容系数，ρ为材料密度。

可以看出，摩擦盘接受了大部分的热量，因此研究系统的发热问题，应以摩擦盘为主要研究对象。

3 仿真结果和分析

(1)压力对摩擦盘温度场的影响

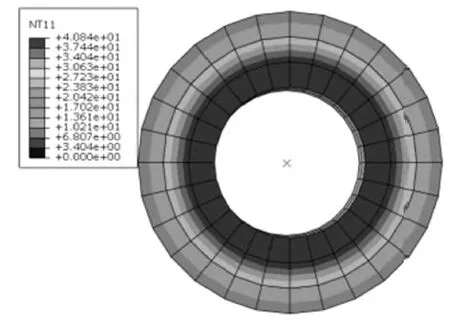
图3 压力为2 MPa时温度场分布

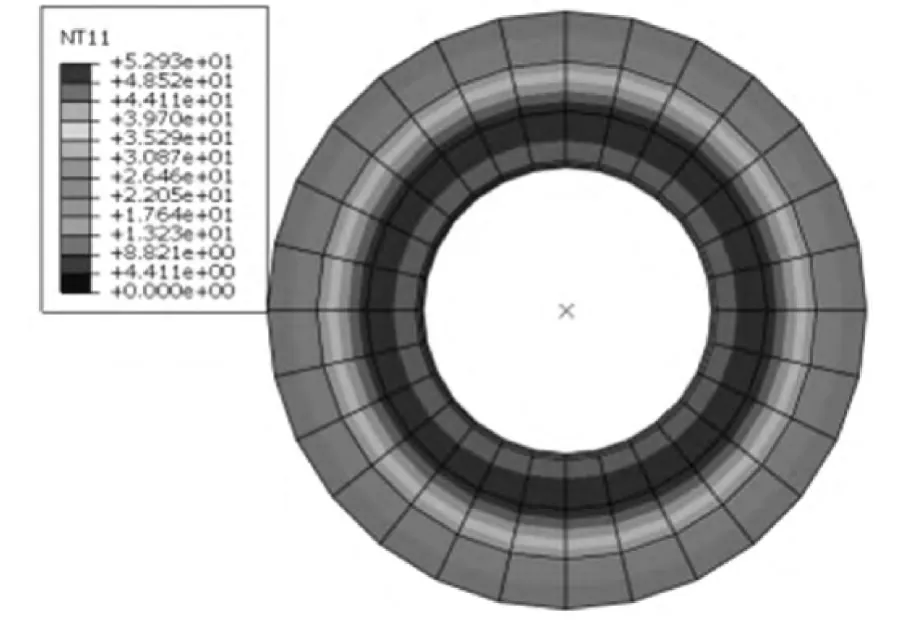
图4 压力为3 MPa时温度场分布

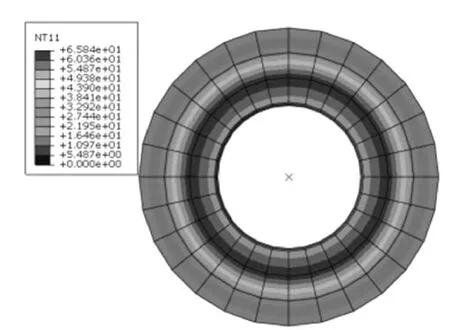
图5 压力为4 MPa时温度场分布

图6 压力为5 MPa时温度场分布

根据上述不同压力下的温度场分布，绘制出转速一定、不同压力下摩擦盘接触面温度值随时间的变化曲线如图7所示。可以发现，随着时间的延长，摩擦盘的温度呈上升的态势，在刚开始阶段，上升速度较快，随着摩擦时间的加长，上升速度有减缓的趋势;摩擦盘接触界面上的温度值与摩擦盘所受得压力成正比，施加压力越大，温度值越高;由此可见，压力是影响温度场的一个重要的因素。

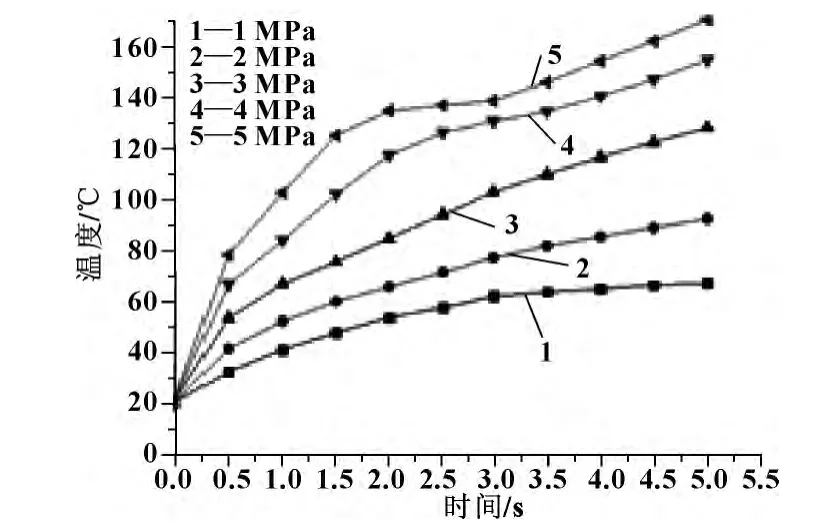
图7 不同压力下摩擦盘温度的变化曲线

(2)转速对摩擦盘温度场的影响

图8—11是t=0.5 s、转速分别为200、300、400、500 r/min时，摩擦盘上温度场的分布情况。可以看出:随着相对转速不断增大，温度场高温区域的温度值也逐渐升高。同时高温区(图中的黑色区域)的面积越来越集中。另外，温度场梯度性分布的特点也越来越明显。出现梯度性的原因和上述(1)中原因类似，在此不再一一赘述。

图8 转速为200 r/min时温度场分布

图9 转速为300 r/min时温度场分布

图10 转速为400 r/min时温度场分布

图11 转速为500 r/min时温度场分布

图12为压力一定、不同转速情况下，摩擦盘接触面上的温度值随时间的变化曲线。可以发现，随着时间的延长，摩擦盘的温度呈上升的态势，在刚开始阶段，上升速度较快，随着摩擦时间的加长，上升速度有减缓的趋势;摩擦盘接触界面上的温度值与摩擦盘/片之间的转速成正比，转速越大，温度值越高。由此可见，转速是影响温度场的一个重要的因素。

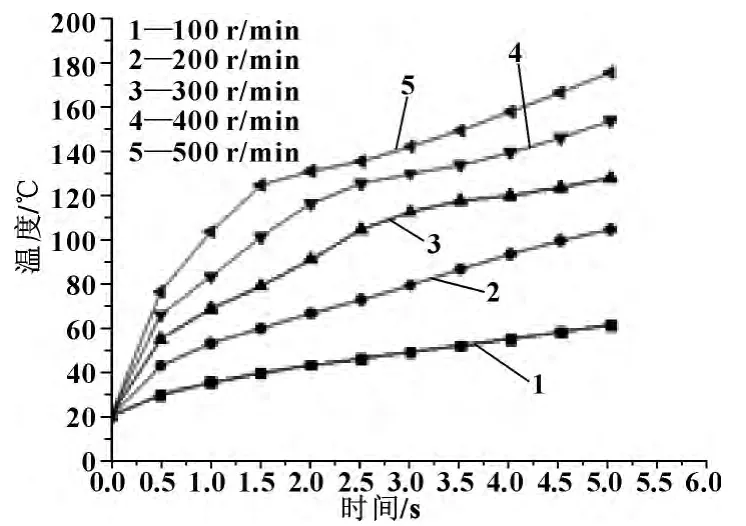
图12 不同转速下摩擦盘温度的变化曲线

(3)考虑通风冷却情况下，摩擦盘温度场仿真

从上述(1)和(2)中可以看到，系统在工作过程中，会因为摩擦副的存在而产生大量的热量，而温度是影响摩擦副之间摩擦因数稳定性的一个最关键的因素。大量的热能积聚在摩擦接触界面上，如果不能及时得到疏散，就会造成摩擦因数随热能的不断积聚不断发生变化，从而影响摩擦加载力矩的输出。考虑到这种情况，决定采用人工的方法，在摩擦盘周围利用风机实行通风冷却。这就能加快摩擦盘与周围空气环境的热交换，加大了接触界面上温度的扩散速度，进而达到降温冷却的目的。

如图13所示为未加入通风冷却与加入通风冷却之后，摩擦盘表面上的温度值随时间变化的曲线。从图13加入通风冷却前后的曲线对比中，可以发现:采取通风冷却的方式，在ABAQUS，将摩擦盘与周围空气的对流换热系数提高到80 W/(m2K)时，明显比未加入冷却时降低了很多，而且温度上升的速率也明显减小，在一定程度上缓解了摩擦因数因热能的积聚发生波动的情况，达到了降温冷却的目的。

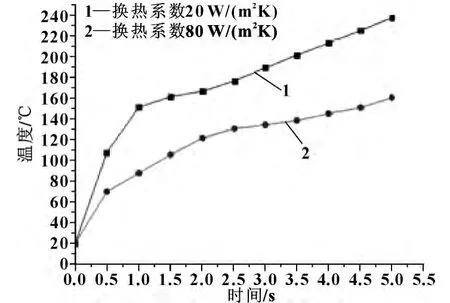
图13 冷却前后摩擦盘温度曲线

4 结束语

根据热力学理论和热－结构耦合原理分析，推导出摩擦盘温度场的数学模型，获得了求解接触界面上温度场的基本理论和分析方法，为进行有限元分析、系统发热冷却问题以及液压控制参数影响因素分析的研究提供了有力的理论基础。在利用有限元软件ABAQUS对摩擦盘进行仿真分析时，给出了摩擦盘进行数值仿真分析的前提假设、主要参数以及所需要的边界条件。并对压力一定、不同速度和速度一定、不同压力两种情况下的具体温度场如何展开了进一步的仿真分析。总结得出压力和速度对摩擦盘上温度场的影响规律，为后续进行负载模拟器的液压控制系统的研究提供了重要而且关键的理论模型和仿真数据。

［1］马晓峰．ABAQUS有限元分析从入门到精通［M］．北京:清华大学出版社，2013．

［2］陆山．热结构分析有限元程序设计［M］．西安:西北工业大学出版社，2003．

［3］苏海赋．盘式制动器热机耦合有限元分析［D］．广州:华南理工大学，2011．

［4］WANG P H，WU X，JEON Y B．Thermal-mechanical Coupled Simulation of a Solid Brake Dics in Repeated Braking Cycles［J］．Journal of Engineering Tribology，2009，11:1041－1048．

［5］OKMURA T，YUMOTO H．Fundamental Study on Thermal Behavior of Brake Dics［J］．SAE Paper，2006，11:201－205．

［6］QI H S，DAY A J．Investigation of Disc/pad Interface Temperatures in Friction Braking［J］．Wear，2007，262:505－513．

［7］CHOI J H，LEE I．Finite Element Analysis of Transient Thermoelastic Behaviors in Disk Brakes［J］．Wear，2004，257:47－58．

［8］俞昌铭．热传导及其数值分析［M］．北京:清华大学出版社，1982．

［9］徐新琦，成学军．热－机耦合分析的有限元法及其应用［J］．海军航空工程学院学报，2004，19(3):380－382．

［10］杨世铭，陶文铨．传热学［M］．3版．北京:高等教育出版社，1998．