龙门式矫直机液压伺服控制系统建模与仿真

方学红，康健，李新有

(1.重庆赛迪冶炼装备系统集成工程技术研究中心有限公司，重庆 400013;2.中冶赛迪工程技术股份有限公司，重庆 401122)

0 前言

龙门式多辊矫直机，通过垂直调整装置来调整矫直辊缝，采用液压伺服控制的方式来控制矫直过程，实现高精度矫直。

对液压伺服控制系统的建模与仿真研究很多，陈永清［1］、阎晓珊等［2］采用传递函数的方式建立了液压伺服控制系统的仿真模型，其特点是系统建模采用机理建模和传递函数描述方式，将液压元件简化为数学函数，将负载用多阶传递函数来描述。这种仿真模型由于对实际系统进行了很多简化，没有充分考虑伺服阀的流量饱和、管道油容积、油液压缩性和液压机械耦合特性等非线性因素对系统响应特性的影响，其仿真结果精度不高，难以反映实际系统的综合性能。为提高仿真精度，了解元件非线性因素以及负载耦合特性对系统响应特性的影响，在受力分析的基础上，根据垂直调整装置的控制模型，采用Matlab中的SimMechanics等模块建立了仿真模型并进行了综合仿真分析，得到了液压伺服系统的动态响应特性，为龙门式矫直机液压伺服控制系统的优化设计提供了新方法。

1 系统工作原理

1.1 系统组成

矫直辊垂直调整装置由液压缸驱动，分别作用在R2、R4、R6和R8上矫直辊的操作侧和传动侧，如图1所示。

图1 垂直调整装置机构简图

液压伺服系统由伺服阀、减压阀、管路和液压缸等组成，根据压下制度调整上矫直辊的位置实现矫直辊缝的调整，同时施加一定矫直力，防止矫直时矫件在竖直方向的串动，为保证设备安全，液压系统具备过载保护功能。

1.2 控制模型

液压缸为单作用缸，通过一个带内置放大器和阀芯位置反馈的伺服阀单腔控制，由负载力回程，无杆腔通过三通减压阀保持恒定压力。矫直辊缝的调整位置由闭环控制系统给定，其控制模型如图2所示。

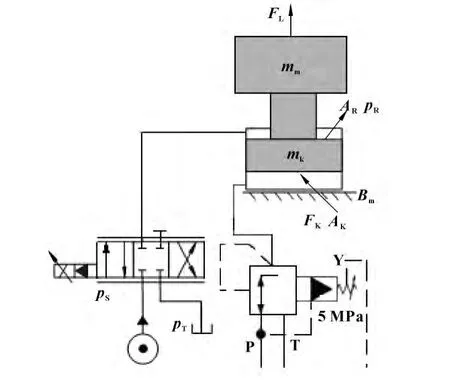
图2 垂直调整装置控制模型

2 系统建模

在研究液压伺服系统的动态特性时，负载通常指液压缸活塞在运动时所遇到的惯性力FL，黏性阻尼力FV，弹性力FP和任意外负载力Fr［3］。系统运动时要克服的力F可用下式表示。

式中:Fr为任意外负载力，是摩擦力、重力等外负载力的合力。

2.1 负载模型

实际的机械系统往往是一个复杂的多自由度分布质量系统，分析计算十分复杂，为了便于理论研究，需要对机械系统进行简化，一般等效为单自由度物理系统［3］。为便于分析建模，将垂直调整装置的负载简化为单自由度物理系统来分析，如图3所示。

图3 垂直调整装置单自由度负载模型

其负载轨迹方程描述如下。

式中:mp为负载等效质量，kg;

Bp为黏性阻尼系数，s·N/m;

Kp为负载等效刚度，N/m;

Fr为任意外负载力，N。

2.2 仿真框图

由于液体的压缩性，当活塞受到外力作用时产生位移，使一腔的压力升高，另一腔的压力降低，被压缩的液体产生的复位力与活塞位移成比例，因此被压缩液压的作用相当于一个液压弹簧，液压弹簧与负载质量相互作用构成一个液压弹簧－质量系统［4］。

针对图2所示的控制模型，将龙门式矫直机垂直调整装置的液压伺服系统简化后建立仿真框图如图4所示。

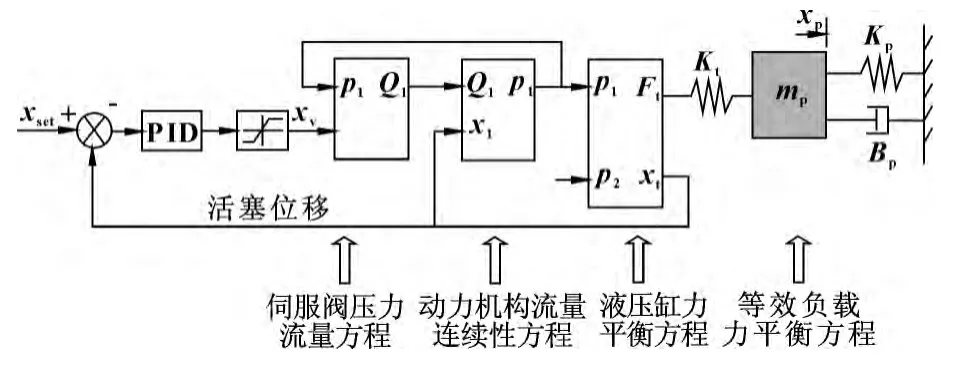
图4 垂直调整装置仿真框图

其中各框图对应的数学方程如下:

(1)伺服阀压力－流量方程

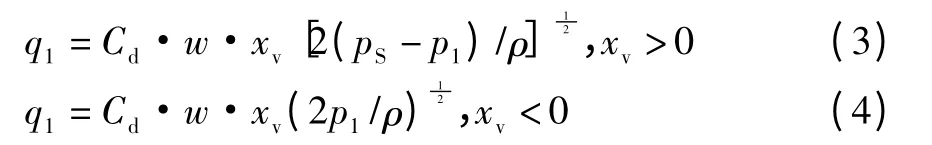
当液压缸缩回时，xv＞0，当液压缸伸出时，xv＜0。

式中:cd为伺服阀流量系数;

w为阀芯面积梯度(开口周边总长)，m;

xv为伺服阀阀芯开度，m;

ps为液压油源压力，Pa;

p1为有杆腔工作压力，Pa;

ρ为油液密度，kg/m3。

(2)动力机构流量连续性方程

式中:A1为有杆腔工作面积，m2;

V1为有杆腔容积，m3;

Cip为液压缸内泄漏系数，m5/N·S;

Cep为液压缸外泄漏系数，m5/N·S;

βe为液体的有效容积弹性模量。

(3)液压缸力平衡方程

式中:mt为活塞等效运动总质量，kg;

xt为液压缸活塞位移，m;

Ay为液压缸有杆腔面积，m2;

Aw为液压缸无杆腔面积，m2。

液压弹簧复位力与活塞位移和负载位移间的关系为:

(4)等效负载力平衡方程

式中:Bp为负载的黏性阻尼系数，N·s/m;

Kp为负载弹簧刚度，N/m;

Fr为作用在活塞上的外负载力，N;

mp为负载等效到活塞上运动总质量，kg。

2.3 综合建模

以往液压伺服系统的建模都采用传递函数的形式对伺服阀和负载进行描述［5－6］，没有充分考虑伺服阀流量饱和，管道油容积、油液压缩性和液压机械耦合特性等非线性因素对系统响应性能的影响，其仿真模型难以真实反映系统综合性能。为了充分考虑这些非线性因素，应用Matlab的Simulink工具箱和SimScape相关的机械、液压和物理信号库［7］，分别建立了阀控缸仿真模块和负载仿真模块。

(1)阀控缸建模

根据伺服阀压力－流量方程(4)和动力机构流量连续性方程(5)，充分考虑伺服阀流量饱和，管道油容积、油液压缩性等非线性因素建立阀控缸子模块如图5所示。

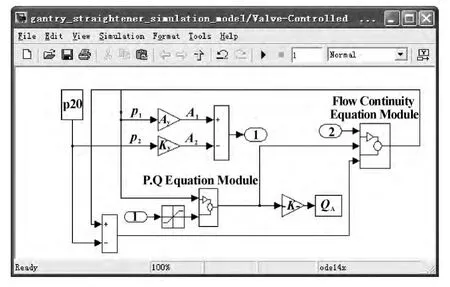
图5 阀控缸子模块

伺服阀压力－流量方程子模块如图6所示。

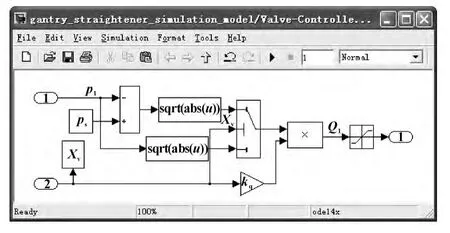
图6 伺服阀压力－流量方程子模块

动力机构流量连续性方程子模块如图7所示。

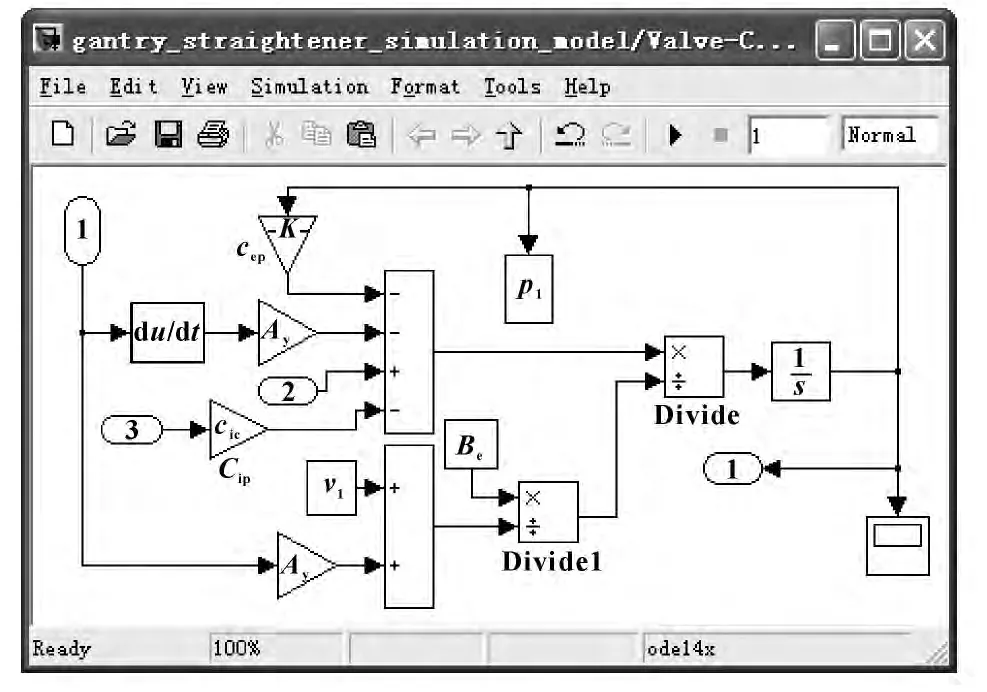
图7 流量连续性方程子模块

(2)负载建模

根据负载简化模型，充分考虑液压机械耦合特性等非线性因素对系统响应特性的影响，按照液压缸力平衡方程(6)、(7)和等效负载力平衡方程(8)表达的负载与液压之间的耦合关系，建立负载子模块如图8所示。

图8 负载子模块

(3)综合仿真模型

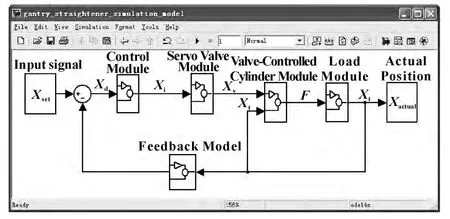
图9 综合仿真模型

按模块化的设计思路分别建立输入信号、控制模块、伺服阀模块和实际响应等子模块，得到该装置液压伺服控制系统的综合仿真模型如图9所示。

3 仿真分析

为描述综合仿真模型中的参数，建立了M文件，仿真初始条件:负载力为150 t，无杆腔背压为3 MPa，液压缸初始位置为250 mm，输入信号为25μm位置阶跃，通过运行M文件并修改相关控制参数，得到系统动态特性曲线如图10所示。

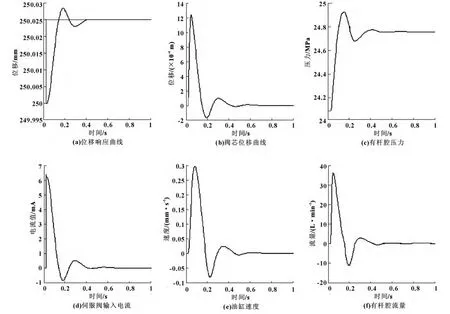
图10 25μm位置阶跃响应曲线

给定初始条件下的仿真结果如表1所示。

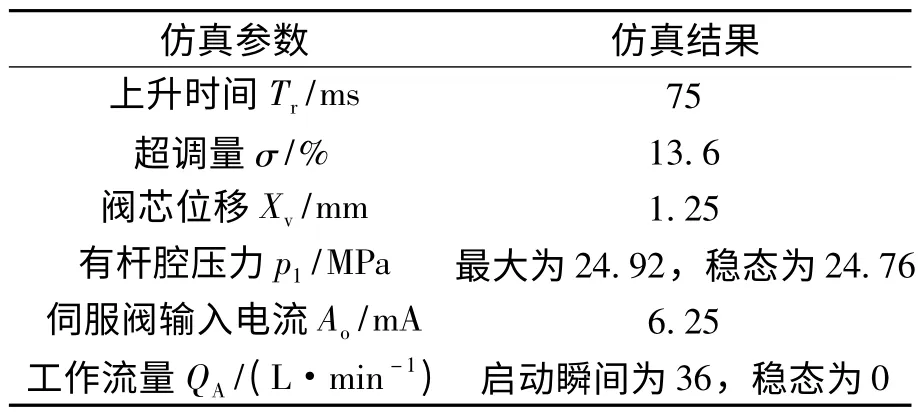
表1 25μm位置阶跃仿真结果

仿真结果表明该液压伺服控制系统的仿真模型建立正确，负载条件下的阶跃响应稳定可靠，快速性好，动态调节性能满足龙门式矫直机辊缝调整的工作要求。

4 结束语

针对龙门式矫直机垂直调整装置液压伺服控制系统，通过原理分析和模型简化，得到了该系统的控制模型，在充分考虑了伺服阀流量饱和，管道油容积、油液压缩性和液压机械耦合特性等非线性因素的基础上，应用Matlab的Simulink工具箱和SimScape相关的机械、液压和物理信号库，建立了该系统的综合仿真模型。仿真分析结果表明，这种建模方式比传统传递函数建模方式更直观，液压机械耦合度更高，仿真结果更准确。

［1］陈永清，徐其彬，徐新和，等．基于Simulink的液压闭环位置控制系统建模与仿真［J］．机床与液压，2013，41(21):138－142．

［2］阎晓珊，刘玉绒．三通阀控单作用缸电液伺服系统的建模与仿真［J］．机床与液压，2013，41(4):92－99．

［3］王春行．液压控制系统［M］．北京:机械工业出版社，2003:40－73．

［4］刘长年．液压伺服系统优化设计理论［M］．北京:冶金工业出版社，1989:8－12．

［5］张国生．基于Simulink的阀控不对称缸速度特性分析［J］．液压气动与密封，2013(1):26－29．

［6］韩虎，刘印锋，孙成通，等．基于MATLAB液压系统的仿真技术研究与应用［J］．液压气动与密封，2007(3):4－5．

［7］SimMechanics User's Guide R2012［M］．The MathWorks，Inc．2012．