指数分布条件下基于事后维修的综合重要度分析

王 宁，王 喆，李淑敏，蔡志强

（1.长安大学 汽车学院，西安710064；2.西北工业大学 机电学院／现代设计与集成制造教育部重点实验室，西安710072）

重要度是指系统中单个或多个组（部）件失效或状态改变时，其对系统可靠性的影响程度，它是组（部）件可靠性参数和系统结构的函数［1］.在系统设计阶段，重要度计算用来帮助设计人员识别系统薄弱环节，为整个系统可靠性提升和优化设计提供支撑依据；在系统运行阶段，重要度分析用于合理分配维修资源，从而保证维修成本降低和系统的正常运行［2］.1969年Birnbaum首次针对二态系统提出了重要度计算方法，随后研究者基于Birnbaum重要度相继提出了风险减少当量（Risk Reduction Worth，RRW）、风险增加当量（Risk Achievement Worth，RAW）、Russell-Vesely等重要度［3］.随着可靠性理论及工程的进步，重要度理论得到了长足的发展，并在核能、复杂装备等可靠性分析、安全性分析、风险分析等领域得到了广泛的应用［4－10］.

综合重要度（Integrated Importance Measure，IIM）综合考虑了组（部）件状态概率、状态转移率及其对系统可靠性影响.根据可靠性浴盆曲线，在早期失效期，转移率呈递减变化；在偶尔失效期，转移率趋向平稳；在磨损失效期，转移率呈递增变化.在组（部）件的全生命周期中，由于转移率随着时间变化，导致组（部）件的状态转移概率也随着时间变化.因此，利用综合重要度能够准确评估面向全生命周期的组（部）件及其状态对系统可靠性或性能影响.综合重要度面向维修过程的物理意义为：单位时间内组（部）件从一个状态提升到另一个状态时，系统可靠性或性能提升的数学期望［11］.文献［12-13］重点研究了二态和多态系统一般综合重要度计算方法及其在串联、并联系统中的性质和相关定理.然而很多工程系统如核能系统，输送系统等都可以直接抽取为串－并联、并－串联等混联系统模型，串联和并联两种基本系统模型难以直接满足系统分析的需要.文中针对典型的二态混联系统（并－串联系统、串－并系统），研究其指数分布条件下基于事后维修的综合重要度计算公式及其相关性质，以便于综合重要度计算方法在二态混联系统中的推广应用.

1 二态系统综合重要度

1.1 二态系统模型

文中以带有劣化特征的二态系统作为研究目标，其模型满足以下几个方面.

1）系统S由n个组（部）件 ｛C1，C2，…，Cn｝构成，且各个组（部）件可靠性分布相互独立；

2）系统及组（部）件变量均只有两种无交集状态，即Ci＝1表示组（部）件Ci正常工作，Ci＝0表示组（部）件发生故障需要维修或者更换；

3）R表示系统可靠性，R＝P（S＝1），Pi表示组（部）件Ci的可靠性，即Pi＝P（Ci＝1）；

4）如果存在q1＞q2，则有P（S＝1｜Ci＝q1）＞P（S＝1｜Ci＝q2）.也就是说，提高某个组（部）件的可靠性必然导致系统可靠性的提升；

5）文中只研究事后维修策略，即组（部）件发生故障时进行维修；

6）对于二态系统，文中仅考虑系统劣化状态，即只有0和1两种状态，研究从1劣化到0状态时重要度的变化过程.

1.2 综合重要度计算

由文献［11］可得二态系统综合重要度计算公式为

公式（1）可表述为

2 二态混联系统综合重要度计算

2.1 事后维修策略

事后维修是指在组（部）件发生故障或性能下降到合格水平以下时所进行的非计划性维修.事后维修策略示意图如图1所示.其中Ti为两次事后维修之间的时间间隔，t1，t2，…，t5为事后维修时间.

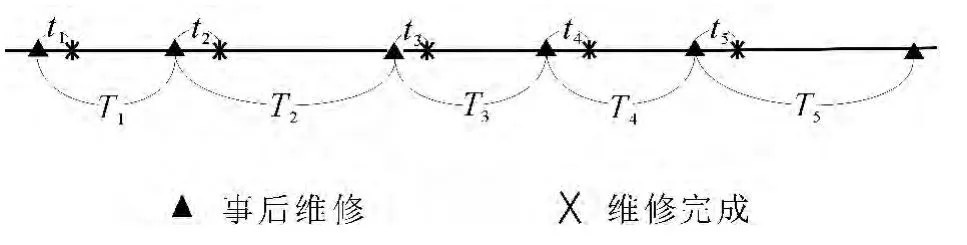
图1 事后维修策略示意图Fig.1 Structure of the correction maintenance

2.2 稳态可用度

假定在（n＋1）次独立重复试验中，每次试验的失效时间、维修时间都服从均值为1／λ和1／μ的指数分布.λ为失效率，μ为维修率，A为转移矩阵，p0为发生故障的概率，p1为正常工作的概率.则

则有

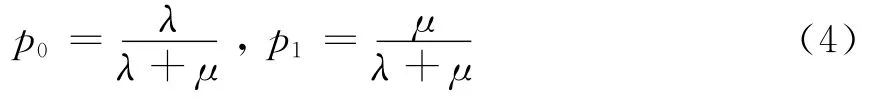
由公式（4）可以看出，指数分布下组（部）件失效的概率和正常工作的概率可通过组（部）件的失效率和维修率来计算.

2.3 系统综合重要度

2.3.1 典型混联系统重要度

1）并－串联系统

并-串联系统结构是由N（N≥1）个串联系统并联而成的.假定第i个并入的串联系统有Ni个组（部）件（第i层），因此得出此并－串联系统的结构函数为 Φ（X（t）），其中［ij］表示第i层中的第j个组（部）件.并－串联系统的结构框图如图2所示.

图2 并－串联系统Fig.2 Structure of parallel-series system

定理1 在串－并联系统中，

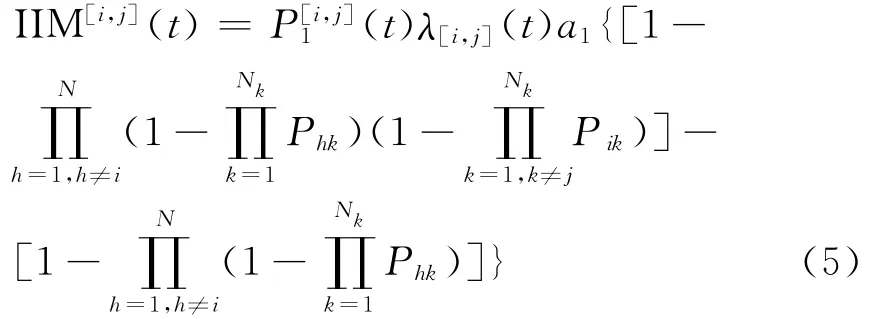
其中Phk＝，h∈［1，N］，k∈［1，Nk］.

公式（5）在并－串联系统中，组（部）件 ［i，j］从状态1降低到状态0的重要度计算方法.

证明 由第1节中公式（1）知，在混联系统中组（部）件重要度为

根据并－串联系统的结构函数可以得出

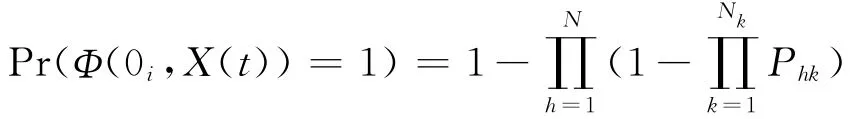
则对于组（部）件 ［i，j］并－串联系统的可靠性公式为

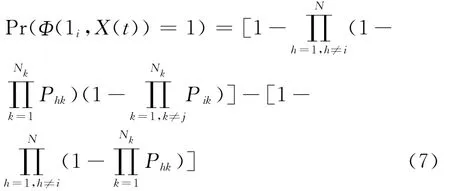
所以二态劣化过程的并－串联系统的综合重要度为

2）串－并联系统

串-并联系统结构是由N（N≥1）个并联系统串联而成的，假定第i个串联的并联系统有Ni个组（部）件（第i层），因此得出此串－并联系统的结构函数为Φ（X（t））＝，并－串联系统的结构框图如图3所示.

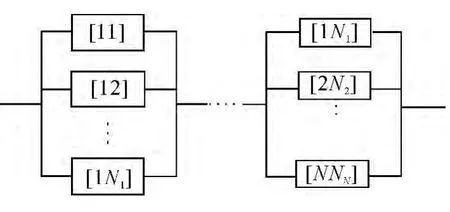
图3 串－并联系统Fig.3 Structure of series-parallel system

定理2 在串－并联系统中，

其中Phk＝，h∈［1，N］，k∈［1，Nk］.

公式（5）表示在串－并联系统中，组（部）件 ［i，j］从状态1降低到状态0的重要度计算方法.

证明 根据图3，由第1节中公式（1）知，在混联系统中组（部）件重要度公式［11］为

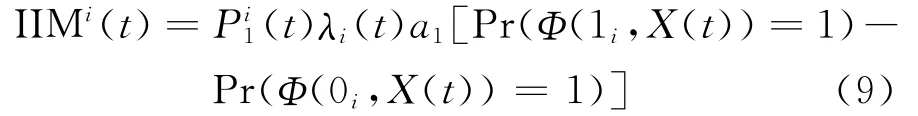
根据串－并联系统的可靠性可以得出

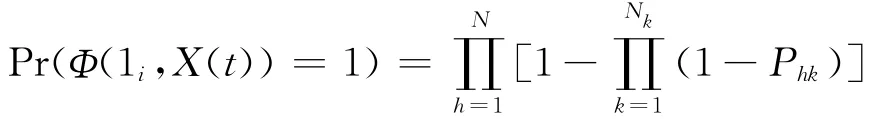
则组（部）件 ［i，j］组成的串－并联系统可靠性公式为

所以，二态劣化过程的串－并联系统的综合重要度为

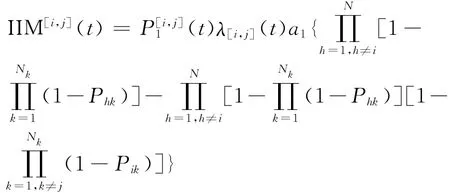
2.3.2 服从指数分布的系统重要度

（1）并－串联系统

定理3 二态劣化的并－串联系统中各个组（部）件均独立且工作与维修时间服从指数分布，组（部）件的综合重要度表达式为

公式（11）二态劣化的并－串联系统中各个组（部）件均独立且工作与维修时间服从指数分布时，组（部）件的综合重要度表达式.

证明 由于需要考虑每个更换时间点的重要度，因此将定理1中推导出的并－串联系统的综合重要度公式（5）中的P0和P1即为公式（3）中求解出的p0和p1，代入可得

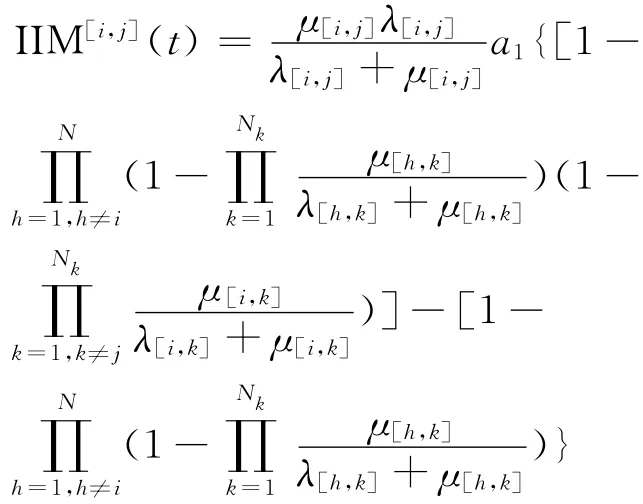
（2）串－并联系统

定理4 二态劣化的串－并联系统中各个组（部）件均独立且工作与维修时间服从指数分布时，组（部）件的综合重要度表达式为

公式（12）二态劣化的串－并联系统中各个组（部）件均独立且工作与维修时间服从指数分布时，组（部）件的综合重要度表达式.

证明 同理，首先引用定理2中推导出的并－串联系统的综合重要度公式（8）为

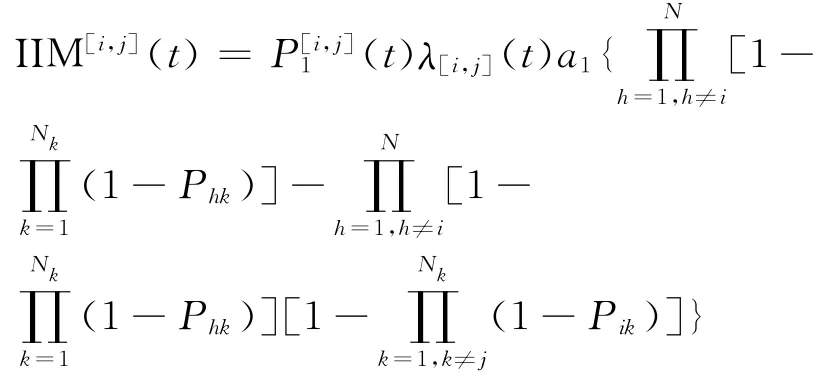
由于需要考虑每个更换时间点的重要度，因此将定理2中推导出的并－串联系统的综合重要度公式（8）中的P0和P1即为公式（4）中求解出的p0和p1，代入可得

3 案例计算与分析

3.1 案 例

考虑一个由五条管道构成的原油运输系统.该系统的结构及部件（管道）的状态空间集成表现在一个框图中，如图4所示［14］.对于任一个管道，假设其容量值被分为0和1两个水平，其中0表示管道失效，即不能传输原油；1表示管道完好，能以最好的状态运输原油.因为原油管道一般都是长期被埋在地下，所以由于内部的堵塞或外部的腐蚀，管道的运输能力会在一定时间后（单位：y）降低甚至失去运输能力.若发现管道的运输能力降低到0水平，就将其更换.部件的性能用传输容量（t／min）来衡量.此混联系统的结构框图为

图4 管道结构图Fig.4 Structure of the pipe

此混联系统结构函数为

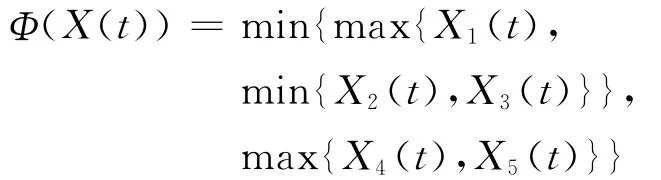
管道的各状态的转移过程如图5所示.

图5 管道的状态转移过程Fig.5 The state transition process of the pipe

3.2 综合重要度计算

假设管道的寿命服从指数分布，给出各个组（部）件的失效率和维修率，见表1.

表1 组 （部）件失效率μi和维修率λi的值Tab.1 The ralues of the failure rateμiand the repair rateλiof the component

由以上给出的数据及系统的结构函数分别求得在更换过程中各个组（部）件的综合重要度，计算表达式为

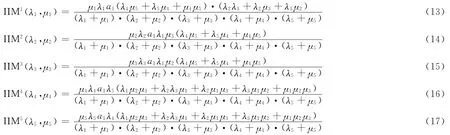
各部件重要度排序如下

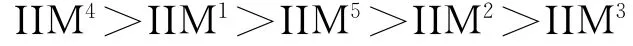
此外，当 （λi，μi）发生变化时，可以求得综合重要度随组（部）件维修率和失效率的变化过程.

3.3 影响因素分析

以组（部）件1为例来说明IIMi（λi，μi）随着λi和μi的变化情况，如图6和图7所示.

假设维修率不变时，组（部）件1的综合重要度随着失效率的变化情况如图6（a）所示.由公式（8）可知，IIM1（λ1，μ1）是关于λ1的增函数，由图6（a）可知，随着失效率的增加，综合重要度越来越大，因此系统设计者应该关注组（部）件的失效率.

假设失效率不变时，组（部）件1的综合重要度随着失效率的变化情况如图6（a）所示，从公式（13）可知，λ1和μ1地位平等，组（部）件1的综合重要度随着失效率和维修率的增加而增大，即图6（a）和图6（b）相同，因为在指数分布中，失效率和维修率共同描述了组（部）件的状态概率分布.

图7（a）和图7（b）给出了当失效率λ1和维修率μ1共同变化时，组（部）件1综合重要度的变化情况.在图7（a）中，失效率λ1和维修率μ1同时增加，综合重要度也随其增加.从公式（13）可知，组（部）件1的综合重要度是关于λ1和μ1的增函数，这与图7（a）相符合.因为在公式（13）中，λ1和μ1的地位是等价的，所以7（a）是关于λ1和μ1的等价点对称的，即关于 （0，0）→ （10，10）对称.

在图7（b）中，失效率λ1逐渐增大，维修率μ1逐渐变小，该曲面随着λ1增大而变高，随着维修率μ1变小而变低.因为失效率λ1逐渐增大，维修率μ1逐渐变小，所以图7（b）的交汇点是（5，5），也是λ1和μ1的等价点，同时图7（b）是关于（5，5）对称的.由图6和图7可知，在指数分布条件下，失效率和维修率是综合重要度的重要指标，二者地位等价.

图6 综合重要度随失效率／维修率变化的二维图Fig.6 The change of IIM with the parameters ofλorμ

图7 综合重要度随失效率和维修率变化的三维图Fig.7 The change of IIM with the parameters ofλandμ

4 结 论

1）针对指数分布条件下基于事后维修的重要度分析问题，基于传统综合重要度计算方法对典型二态混联系统综合重要度计算公式进行了推导，得出典型二态系统综合重要度的等价计算公式.

2）以原油运输系统为案例，对典型二态混联系统组（部）件综合重要度进行了计算和分析.

3）失效率和维修率作为重要度分析的重要指标，在指数分布条件下的二态劣化混联系统中，指数分布条件下组（部）件的综合重要度与失效率和维修率成正相关关系.

［1］ BIRNBAUM Z W.On the Importance of Different Components in a Multi-Component System ［M］.New York：Academic Press，1969.

［2］ RYAN T P，Meeker W Q.System Reliability Theory：Models，Statistical Methods，and Applications ［J］.Journal of Quality Technology，2005，35（1）：84.

［3］ VASSEUR D，LLORY M.International Survey on PSA Figures of Merit［J］.Reliability Engineering and System Safety，1999，66（3）：261.

［4］ 王海涛，吴宜灿，李亚洲，等.核电站实时风险管理系统部件重要度计算方法研究［J］.核科学与工程，2008，28（1）：61.WANG Hai-tao，WU Yi-can，LI Ya-zhou，et al.Study on the Algorithm of the Calculation’of the Components Importance Measures in a Risk Monitor［J］.Chinese Journal of Nuclear Science and Engineering，2008，28（1）：61.（in Chinese）

［5］ LAMBERT H E.Fault Trees for Decision Making in Systems Analysis［D］.Livermore：California University，1975.

［6］ FUSSELL J B.How to Hand-Calculate System Reliability and Safety Characteristics［J］.IEEE Transactions on Reliability，1975，24（3）：169.

［7］ VESELY W E，DAVIS T C，DENNING R S，et al.Measures of Risk Importance and Their Applications［R］.USA：Nuclear Regulatory Commission，NUREG／CR-3385，1983.

［8］ BARLOW R E，PROSCHAN F.Importance of System Components and Fault Tree Events［J］.Stochastic Processes and Their Applications，1975，3（2）：153.

［9］ HONG J S，LIE C H.Joint Reliability-Importance of Two Edges in an Undirected Network ［J］.IEEE Transactions on Reliability，1993，42（1）：17.

［10］ BORGONOVO E，APOSTOLAKIS G E.A New Importance Measure for Risk-Informed Decision Making［J］.Reliability Engineering and System Safety，2001，72（2）：193.

［11］ SI S B，DUI H Y，CAI Z Q，et al.The Integrated Importance Measure of Multi-State Coherent Systems for Maintenance Processes［J］.IEEE Transactions on Reliability，2012，61（2）：266.

［12］ SI S B，DUI H Y，ZHAO X B，et al.Integrated Importance Measure of Component States Based on Loss of System Performance［J］.IEEE Transactions on Reliability，2012，61（1）：192.

［13］ SI S B，CAI Z Q，SUN S D，et al.Integrated Importance Measures of Multi-State Systems Under Uncertainty［J］.Computers and Industrial Engineering，2010，59（4）：921.

［14］ LISNIANSKI A.Extended Block Diagram Method for a Multi-State System Reliability Assessment［J］.Reliability Engineering and System Safety，2007，92（12）：1601.