非对角型齐次抛物方程组弱解的正则性＊

董 艳

（西北工业大学 理学院，西安710129）

文中研究如下形式的非对角型变系数齐次抛物方程组

文献［1］利用Liouville定理研究了欧氏空间中满足自然增长条件的非对角型非齐次椭圆方程组弱解的 Hölder正则性．文献［2］研究了由Hörmander向量场构成的对角型非齐次退化椭圆方程组弱解的部分Hölder正则性．受文献［1-2］的启发，文中研究式（1）弱解的正则性，即利用先验估计法建立弱解梯度的Morrey正则性和弱解的Campanato正则性，最后利用同构引理得到弱解的Hölder正则性．

设式（1）中的系数总满足 aαβij（z，u） ＝Aαβ（z）δij＋Bαβij（z，u），且符合下列假设条件

（H）设Aαβ（z）∈VMO∩L∞，Aαβ（z）＝Aβα（z）满足椭圆性条件，Bαβij（z，u）有界可测，即存在正常数Λ0，μ0，δ，0＜Λ0≤μ0，0＜δ＜1，使得对任意z＝ （x，t）∈ ΩT，ΩT＝ Ω × （0，T）和 任 意ξ ∈R（q＋1）N，有

文中的主要结论为

1 预备知识

对每一个多重指标β＝ （β1，β2，…，βd）（1≤βi≤q，i＝1，…，d，｜β｜＝d），定义长度为d的交换子为Xβ＝ ［Xβd，［Xβd-1，…［Xβ2，…Xβ1］］］．

定义1 如果对每一点x0∈Ω ⊂Rn，｛Xβ（x0）｝｜β｜≤s都能张成欧氏空间 Rn，则称向量场组X＝（X1，…，Xq）是Ω上的s步Hörmander向量场．称Hörmander向量场是自由到s步的，若n＝dimg（q，s），其中g（q，s）是s步的李代数．

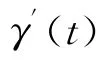
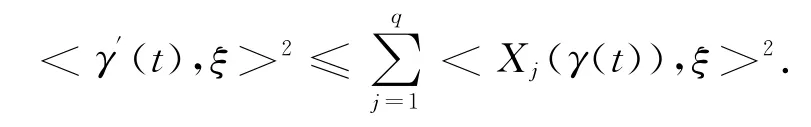
对该次酉曲线，可以定义其长度为lS（γ）＝T．设x，y∈Ω，记Φ（x，y）为连接x和y的所有次酉曲线的集合．对于任意的x，y∈Ω，定义d（x，y）＝inf｛lS（γ）：γ ∈ Φ（x，y）｝为由 X 诱导的 Carnot-Carathéodory距离或次椭圆距离．

由Carnot-Carathéodory距离可定义以x0为中心，R为半径的度量球，形如

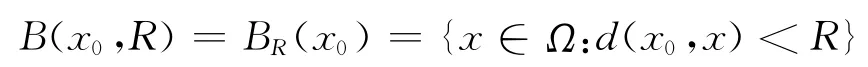
当不考虑中心时，B（x0，R）简记为BR．

由文献［3］可知，对有界集Ω⊂Rn，存在常数cD，RD＞0，使得对任意x0∈Ω，0＜2R ＜RD，B（x0，2R）⊂Ω，有二重性条件成立

｜B（x0，2R）｜≤cD｜B（x0，R）｜，

因此B（x0，R）是一个齐型空间［4］．进一步，对任意的R≤RD和任意的t∈ （0，1），总有

记Q＝log2cD，称Q为Ω上的局部齐次维数．由文献［5］可设存在正常数c1和c2，使得

c1RQ≤｜BR｜≤c2RQ．

设z0＝（x0，t0）∈ΩT⊂Rn＋1，类似于上面定义的度量球，可以定义以z0为顶点的抛物柱体为

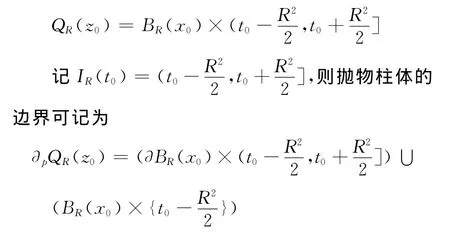
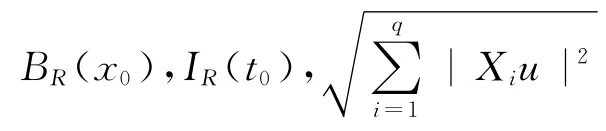
定义3 （抛物Sobolev空间）设m，k为0或1，1≤p＜＋∞．称

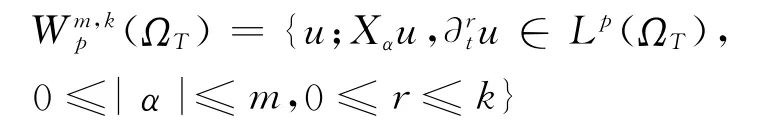
为与Hörmander向量场相关的抛物Sobolev空间，且范数定义为

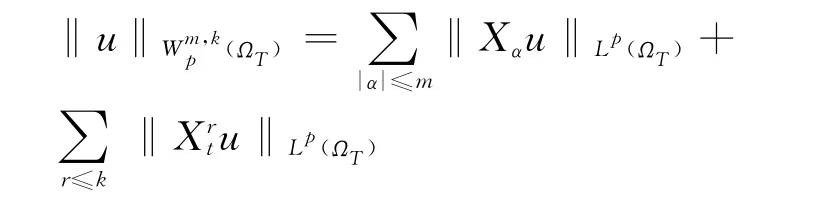
定义4 （Morrey空间）设1≤p＜＋∞，λ＞0，若对任意的f∈Lp（ΩT），成立

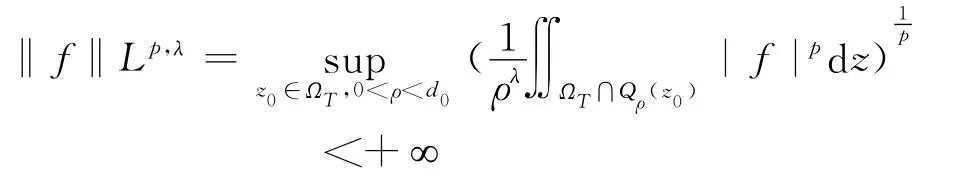
其中d0为柱体ΩT的直径，则称f属于Morrey空间Lp，λ（ΩT）．

2 定理1的证明

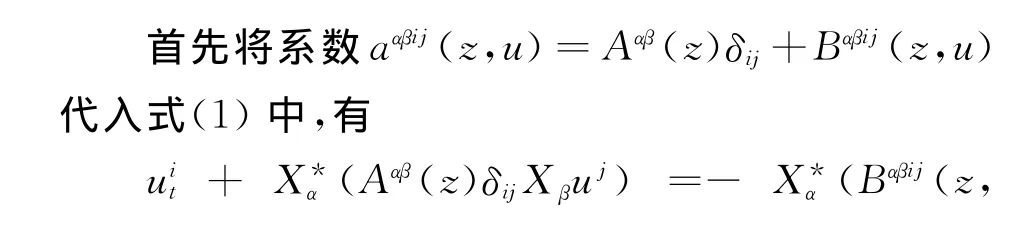
［1］ WIEGNER M．Regularity Theorems for Nondiagonal Elliptic Systems［J］．Ark Mat，1982，20（1）：1．

［2］ GAO D，NIU P C，WANG J L．Partial Regularity for Degenerate Subelliptic Systems Associated with Hörmander’s Vector Fields［J］．Nonlinear Anal，2010，73（10）：3209．

［3］ NAGEL A，STEIN E M，WAINGER S．Balls and Metrics Defined by Vector Fields I：Basic Properties［J］．Acta Mathematica，1985，155（1／2）：103．

［4］ GIANAZZA U．Regularity for Nonlinear Equations Involving Square Hörmander Operators［J］．Nonlinear Anal，1994，23（1）：49．

［5］ XU C J，ZUILY C．Higher Interior Regularity for Quasilinear Subellliptic Systems［J］．Calc Var Partial Dif，1997，5（4）：323．

［6］ MORREY C B．Multiple Integrals in the Calculus of Variations［M］．Heidelberg：Springer Verlag，1966．

［7］ DONG Y．Hölder Regularity for Weak Solutions to Divergence Form Degenerate Quasilinear Parabolic Systems［J］．J Math Anal Appl，2014，410（1）：375．

［8］ MEYERS N．Mean Oscillation over Cubes and Hölder Continuity［J］．Proc Amer Math Soc，1964，15（1）：717．