非对称铺层在复合材料大开口结构中的应用分析

李玉亮，涂卫军，刘慧慧，王艳丽，蒋若冰

（1.中航工业洪都,江西 南昌330024；2.空军驻江西地区军事代表室，江西 南昌330024）

0 引 言

纤维增强树脂基复合材料具有比强度和比模量高；可设计性强；耐疲劳性能、阻尼性能和耐腐蚀性能好等优点，已广泛应用于飞行器结构中。同时，复合材料在固化过程中，其力学性能和内应力在时间、空间的分布具有非均匀、非稳态和强耦合等特点，固化成型过程中产生的残余应力和变形使得复合材料结构的成型精度难以控制。特别是对于一些大开口圆柱壳结构，其成型过程中的温度与成型后使用温度相差较大，固化后容易产生翘曲变形。为了消除复合材料大开口结构的热翘曲变形，提高产品成型精度，本文对非对称层合板固化变形规律进行了研究。

Hyer[1]采用能量法研究非对称层合板的固化变形，认为层合板的变形行为与板的尺寸有密切关系。Cowley[2]等将正交层合板固化变形近似为柱面形状，应用经典层合板理论给出了该柱面曲率变形的估算方法。随着经典复合材料层合板理论的日趋成熟，已成为研究复合材料热翘曲变形的有利工具。张纪奎[3]等利用三维有限元模型研究固化度与固化收缩对非对称复合材料层合板固化变形的影响。本文采用三维有限元的方法，研究了非对称层合板在热载荷、固化收缩、模具加热变形作用下的固化变形情况。首先通过计算层合板固化过程温度和固化过程，然后采用“瞬时线弹性”模型[4]将数值力学性能表示为温度和固化度的函数，通过LUSAS公司的LUSAS HPM（High Precision Molding）软件，模拟了不同非对称结构，分析了对大开口圆柱壳结构固化后变形的影响。

1 基本假设

对于任意铺层的复合材料矩形层压板结构，铺层可以是非对称和非均衡的。层压板的几何形状和坐标系如图1所示。其中坐标原点设在层压板的几何中心，z轴沿壳体的厚度方向，x、y、z轴遵循右手法则。沿x、y、z轴方向的位移分别标记为u、v、w。另外假设：

1)垂直于层压板中面方向的正应变很小，可以忽略不计；

2)层压板中面法线在变形过程中保持为直线，且中面法线与其垂直线段之间的直角也保持不变，这意味着忽略该两方向的剪应变；

3)与中面平行的截面上的正应力远小于其垂直面上的正应力，因此可以忽略。

图1 复合材料层压板坐标系

2 本构关系

2.1 单向层合板的偏轴热膨胀系数

当单向板不考虑任何外载荷作用、仅受到一个均匀的ΔT温度变化时，则会引起单向板膨胀变形。由于复合材料单向板是正交各向异性，所以受湿热影响后，只发生纵向和横向的变形，而不会发生纵横向角变形。所以在单向板主方向的湿热应变为：

而αx,αy,αxy可以依照上面的应变转换公式（1），分别由主方向的α1,α2求得：

2.2 层压板的热应力

假设对于复合材料层压板第k层，其应力-应变关系是弹性的：

式（3）中Cij是k铺层在整体坐标下的刚度系数，由基本假设可以认为：复合材料层合板中横向剪应变γxz，γyx和横向正应力σz足够小，可以忽略不计，这时的应力-应变关系可以简化为：

当层合板受外载荷的作用，且又受温度变化的影响时，在线性理论中，由这两种因素引起的应变仍然可以进行叠加。因此，第k层非主方向应力-应变热弹性关系式可以写为：

由假设可知直线法假设成立，有：

将式（6）代入（8）后，得：

2.3 有限元方程的建立

复合材料固化成型过程影响固化残余应力和变形的因素可以归为4类：热胀冷缩效应、树脂基体的固化收缩效应、结构与模具之间的相互作用以及温度、固化度和树脂流动的空间不均匀性引起的材料性能差异。

对于正交各向异性材料，热载荷与固化收缩载荷引起的总自由应变εTC为：

式中：εTC表示温度和固化度变化引起的应变矩阵；ΔT、ΔC分别表示温度和固化度变化量；α1、α2、α3和β1、β2、β3分别为材料在3个主方向上的热膨胀系数和固化收缩系数。

由温度和固化度变化引起的单元载荷列阵可表示为：

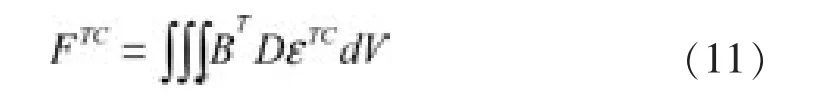
式中：FTC为温度和固化度引起的单元载荷列阵；B为应变矩阵；D为弹性矩阵；V为单元体积。

忽略惯性力和黏性力的作用，只考虑热载荷和固化收缩载荷的准静态平衡方程为：

式中：K为单元刚度矩阵；δ为单元节点位移向量。

3 算例数值仿真

基于以上有限元模型，使用LUSAS HPM软件对不同铺层情况的热翘曲变形进行预测。算例采用HF40/EH103/40平纹织物预浸料（工程常数为：E11= 60Gpa；E22=60Gpa；G12=4Gpa；ν11=0.3；α11=0.19× 10-6/℃；α22=40.3×10-6/℃），铺层形式为2 X(45/-45/ 45/-45/04)/SYM，理论厚度为7.04mm。制成曲率变形为R=500mm的开口圆柱层合板，长度为l= 400mm。室温20℃，固化温度制度如图2所示。

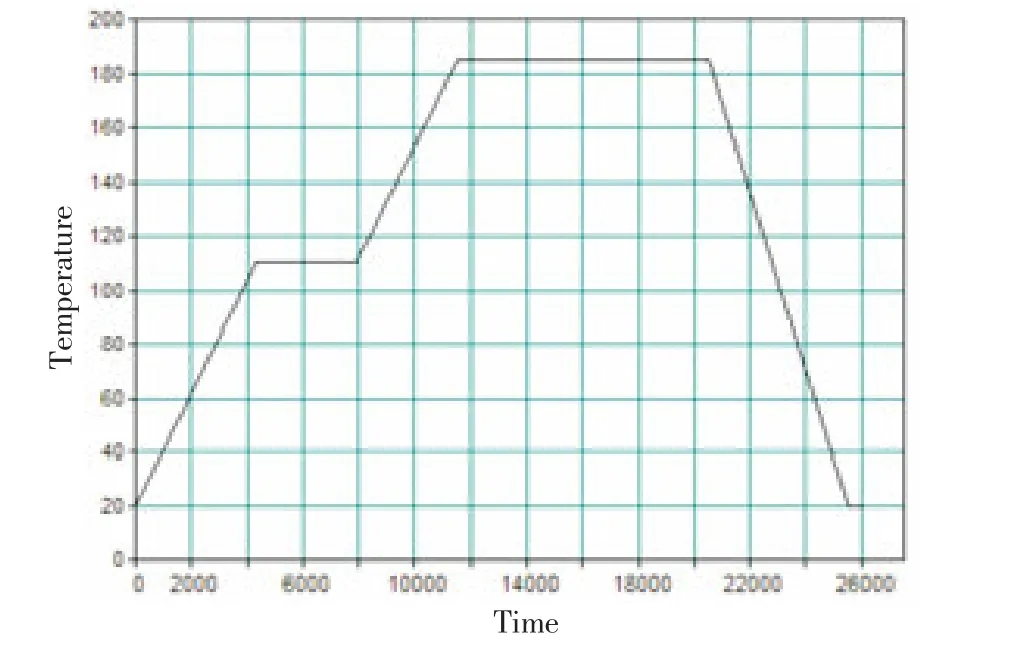
图2 复合材料固化制度

使用 LUSAS HPM计算获得该固化制度下，EH103树脂的固化度、树脂状态、Tg变化及树脂收缩率等情况，如图3~图6所示。

考虑到精确模拟复合材料开口圆柱层合板的固化形状，有限元模型中采用了200个四节点四边形壳单元。为了消除刚体位移，设定模型左侧节点没有沿坐标轴平动和转动。

图3 树脂固化度

图4 树脂状态

图5 树脂Tg

图6 树脂收缩率

图7给出了有限元模拟的准各向同性铺层下开口圆柱壳的热翘曲变形情况。通过图7可以看到，在准各向同性铺层情况下，由于模具热膨胀系数的差异、树脂收缩及残余应力的影响，制件产生了最大2.77mm的收口变形。

为了研究非对称铺层对开口圆柱壳热翘曲变形的影响，分别模拟了在制件内表面和外表面增加两层90°单向铺层时，制件的翘曲变形情况，如图8、图9所示。

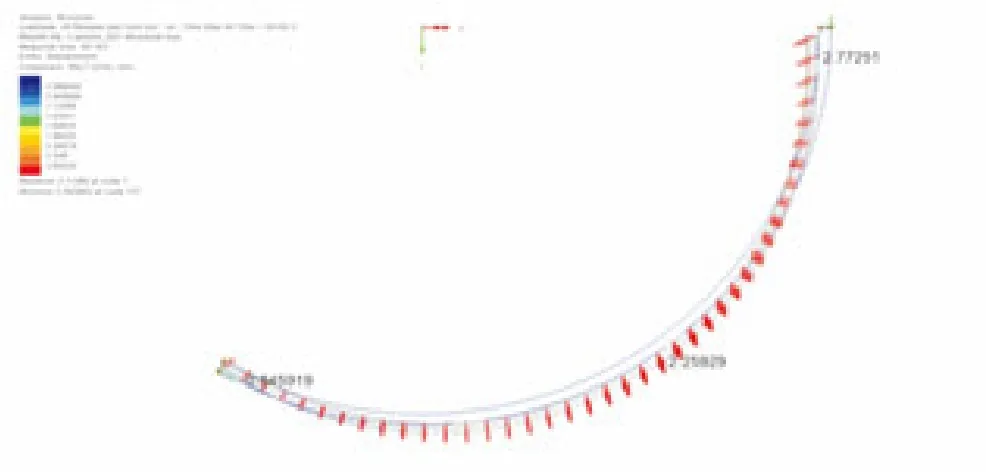
图7 准各向同性情况下制件变形

图10、图11分别给出了内外表面增加两层90°铺层时，制件的热翘曲变形。从图10可以看出，当内表面增加两层90°单向铺层时，制件的热翘曲变形明显减小，左、中、右三段的变形分别为0.3、0.31、0.73mm，层合板的整体结构翘曲内收现象明显减少，说明在内表面增加横向铺层有利于减少树脂收缩、残余应力所引起的翘曲变形。而从图11中可以发现，当外表面增加两层90°单向铺层时，制件的热翘曲变形明显增大，左、中、右三段的变形情况分别为1.48、3.91、4.80mm，这说明当非对称铺层位于外中面时，由于非对称结构所引起的残余应力增加，使得结构的热翘曲变形更为严重。

图8 内表面增加两层90°铺层

图10 内表面增加两层90°铺层后的变形

图9 外表面增加两层90°铺层

图11 外表面增加两层90°铺层后的变形

4 结 语

将固化过程中树脂力学性能的变化与树脂收缩转换为固化度、收缩率与温度的函数，使用LUSAS HPM软件对不同铺层情况下开口结构的热翘曲变形情况进行了研究，建立了热翘曲变形与温度、树脂固化度及树脂收缩率之间的关系。通过计算发现，在开口圆柱层合板内表面增加90°铺层能有效减小因树脂固化收缩和固化残余应力所引起的热翘曲现象，而当非对称铺层出现在开口圆柱层合板外表面时，其热翘曲现象加剧。

[1]Hyer M W.The room-temperature shapes of four-layer unsymmetric cross-ply laminates[J].Journal of Composite Materrials,1982,16(4):318-340.

[2]CowleyK C,BeaumontP W R.The measurement and prediction of residual stresses in carbon-fibre/polymer composites[J].Composite Science and technology,1997,57(11):1445-1455.

[3] 张继奎，郦正能，关志东，程小全.固化度与固化收缩对非对称复合材料层合板固化变形的影响. [J].复合材料学报，2007,24(2):120-124.

[4]Johnston A,Vaziri R,Poursartip A.A plane strain modelforprocess-induced deformation of laminated composite structures [J]. Journal of Composite Materials,2001,35(16):1435-1469.