强化有效驱动 打造高效课堂

金惠萍

摘 要：新一轮教学改革，追求的是高效课堂。而实现课堂高效的关键在于让学生能动起来，成为学习的主体。作为处于主导作用的教师，重点在于如何有效驱动，可从课前的思维内化、贯穿课堂的问题设计、空间留白的创意生成以及师生共鸣的情感投入等方面着手，激发学生的能动性。

关键词：高效课堂；有效驱动；问题；生成

随着教学改革的进一步深入，打造高效课堂成为关注焦点。高效课堂应该是在教师的引导下，学生自主学习的课堂。但目前，我们的课堂主要还是老师的“讲堂”，而不是学生真正的“学堂”，学生“被动”接受的状态比较普遍。同时，学生主体地位的缺失也直接影响了课堂教学的有效性。

转变学生“被动”学习的现状，让每一个学生真正动起来，这是构建高效课堂的关键。那么，教师如何有效驱动呢？笔者认为可从以下几个方面去研究：

一、内化驱动——强基固本，为高效课堂夯实功力

建构主义认为，学习是建构知识的过程，是学习者面对新信息时，利用已有的经验进行自己的解释，生成自己的定义，那么，这一个过程必然不是被动的。因此，教师的角色应该是帮助学生建构生成自身知识。

1.把知识还原。这样，教师便可从根本出发，为学生创设问题解决的情景，引导学生通过分析、归纳、猜想，促进学生新旧知识经验之间的双向的相互作用过程，引发认知结构的重组，使教学进程成为一个动态的、有机的整体。

2.把思维稚化。教师把自己的思维降格到学生的水平，设身处地地揣摩学生的学习水平，用学生的思想和方式去理解知識的构成。例如，在讲授数学归纳法时，很多教师都喜欢用“多米诺骨牌”的例子来讲解。“多米诺骨牌”的事例当然很典型，但学生并不是很熟悉，若采用“学校停车处整齐摆放的一排自行车”，效果也一样很好。

还原与稚化的目的就在于，打开情感阀门与思维按钮，使师生能在课堂上产生“同频共振”。例如，在方程的根与函数的零点教学中，我们可如下设置：

投影：观察图片，你看到了什么？有什么启发？（图中的人物从右侧看是老头，从中间看是老太太，从左侧看是少女）

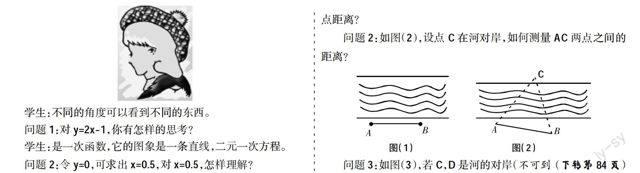
学生：不同的角度可以看到不同的东西。

问题1：对y=2x-1，你有怎样的思考？

学生：是一次函数，它的图象是一条直线，二元一次方程。

问题2：令y=0，可求出x=0.5，对x=0.5，怎样理解？

学生：方程2x-1=0的根，函数的图象与x轴交点的横坐标。

教师：对应于函数呢？0.5还有一个名字，叫函数的零点。

这样的设计可避免两个问题：（1）教材中用二次函数作为载体，一定程度上加重了学习的负担，对概念形成是一个障碍。（2）让学生能从不同角度去看待一个关系式，没有铺垫有些突兀。同时一次函数一样能说明问题，而且学生对一次的理解已经非常到位。因此，这样的创设加工，更符合学生的认知，更适合学生构建零点的概念，也能更有效地让学生动起来。

二、问题驱动——顺水推舟，为高效课堂提升动力

一节好课，是由一连串有价值的有效问题组成的。通过不断追问形成正确的认识，获得深层理解和多元化思路，最终生成学生自己的知识。问题设置可从以下几个方面着手：

1.问题要有效。不问现有发展区内的低效问题，也不问潜在发展区内的无效问题，只有在最近发展区内提问，才能对高效课堂起到推波助澜的作用。

2.问题要有别。我们要分清哪些问题是基础性的问题，就可以用“是什么”“怎么样”来提问；哪些问题是拓展性问题，我们就可以用“你是怎么想的”来提问；哪些问题是探究性问题，有必要让学生讨论、探究。

3.问题要有度。一方面是要选好角度；另一方面是要掌握好难度，要有挑战性，激发学生思考。

例如，在《解三角形应用》教学中，利用三角形解决测物距、测物高、测航距等问题，我们可设计一条问题串，从最直接的能到达的两点距离开始，到中间隔断不能到达的两点距离，再到对面的两点距离，再演变成三维空间的高度问题，环环相扣，层层深入，既能顺水推舟，又能把问题连成知识串，还能节省很多的时间，为高效率达成教学目标奠定基础。案例可设置如下：

问题1：如图（1），现有A，B两点在河同侧，如何测得A，B两点距离？

问题2：如图（2），设点C在河对岸，如何测量AC两点之间的距离？

问题3：如图（3），若C，D是河的对岸（不可到达）平面上两点，如何测量CD距离？

问题4：如图（4），若D是山峰的峰顶，不过河，如何测量CD的高度？

通过这四个问题的创设，构建了整堂课的框架，在不断的追问中，步步紧逼，既可充分调动学生的学习动机，又能保持学生行为的续动力，有效提升自主性。

三、生成驱动——开枝散叶，为高效课堂注入活力

我们都有过这样的尴尬：本来准备好好的一节课，突然被一个学生的不同意见或突如其来的问题而打乱，原本的完美计划被打破，甚至出现尴尬局面。但这可能也正是课堂创意生成的萌芽点，这种机会可遇而不可求，教师需要充分发挥教学机智，给学生提供自由发挥的空间。

上述“解三角形”课中，我就遭遇了一场“意外”。在得到预想解法后，有一学生提出：用同样高度的两个测角仪AE和BF同时测得山顶D的仰角，分别测得仰角为α，β，保证两测角仪与CD在同一平面内，已知AB间的距离，测角仪的高度是b，可求山峰的高度。（方法见图）

这正是后面教学中的一个题型，我顺势提问：若海中有岛A，已知A岛周围8海里内有暗礁，今有一货轮由西向东航行，望见A岛在北偏东75°，航行20海里后，见此岛在北偏东30°，如货轮不改变航向继续前进，问有无触礁危险？

趁势我又让学生把此题进行改编，静态变动态，改造成第三种题型——航海中的追逐问题。这样，原本在备课中没法与前面连成一条问题串的航海问题顺利得到链接，并给它提供了一个更好的平台，降低了动态问题的难度。

四、情感驱动——以情激情，为高效课堂平添魅力

在教学中，我们发现学生在学习一些概念、理论、方法时，并不是无动于衷，而是常常抱有各种不同的态度，有各种复杂的内心体验。虽然这种情感不直接参与认知活动，但对数学学习起着推动、增加、坚持、调节等作用。因此，在课堂教学中，教师要重视学生的情感体验，适时地加以引导。首先，师生必须建立一种和谐的“情感场”，并充分发挥它的作用。其次，教师的情感必须有感染力。波利亚指出：当你讲授一个很熟悉的证明时，摆出一副兴奋的样子，要装出有很多点子，当你证明完时，你还要表示惊奇和得意。此时此刻，学生乐意参与课堂教学，课堂效率自然就提高了。

以上的四种驱动相辅相成，相得益彰，其中内化是根本，问题是关键，生成是活力，情感是保障。通过营造宽松、和谐的课堂氛围，充分发挥教师的教学机智，实施自然生成的方式来激发学生的内驱力，从而促进学生积极主动地进行探究活动，构建高效的课堂教学平台。

参考文献：

章建跃.理解数学 理解学生 理解教学[J].中国数学教育：高中版，2010（12）.

编辑 谢尾合