一种多进制LDPC码加权符号翻转译码算法*
2015-03-25张用宇
张用宇
(中国人民解放军91469部队,北京 100841)
一种多进制LDPC码加权符号翻转译码算法*
张用宇
(中国人民解放军91469部队,北京 100841)
提出了一种低复杂度基于翻转规则的多进制低密度奇偶校验(Low-Density Parity-Check ,LDPC)码符号翻转译码算法。为寻求有效码字,该算法在符号向量空间迭代地更新硬判决的接收符号向量。每一次迭代只改变一个符号,其符号翻转函数综合考虑了不满足校验式的个数和接收比特和计算出符号的可靠性度量。在高阶伽罗华域中采用一种无限环路规避和翻转符号选取方法,同时提出了翻转规则设计方法,该设计决定了计算复杂度和差错性能。仿真结果表明,该符号翻转算法在帧长为150符号的16进制LDPC码中取得了纠错性能和计算复杂度的有效权衡。
多进制;低密度奇偶校验码;迭代译码;翻转规则
0 引 言
低密度奇偶校验(Low-Density Parity-Check,LDPC)码由Gallager于1962年提出的一种基于稀疏校验矩阵的线性分组码[1],在20世纪90年代被重新发现并认为是一类接近Shannon限容量的好码[2]。自从LDPC码的重新发现,其在数字通信系统中的构造、编译码、性能分析和应用成为了研究的热点。目前,许多学者都致力于二进制LDPC码的研究,而对多进制LDPC码的研究正处在发展阶段。
多进制LDPC码的译码[3]根据译码原理可分为四类:硬判决译码、软判决译码、基于可靠性度量的译码和混合译码。1998年,Davey和Mackay在二进制和积算法(Sum-Product Algorithm,SPA)译码的基础上提出了基于GF(q)(q>2)域的多进制LDPC码译码算法QSPA[4],被称为多进制经典译码算法。2000年,Mackay在GF(q)域上提出了FFT-QSPA多进制译码算法[5],将计算的复杂度降低为O(qlog2q),2007年,David Declercq提出了扩展最小和(Extended Min-Sum,EMS)算法[6-7],采用对数似然比值作为传递的信息,在信度传播校验节点上只有一部分(nm≪q)有用值参与度量值的计算,算法复杂度为O(nmq)。2010年,陈超提出了多进制广义比特翻转(Generalized Bit-Flipping,GBF)算法和修正的GBF(MGBF,Modified GBF)算法[8],分别采用信道的硬判决和软判决信息来初始化,算法中每一个符号都采用整数度量,循环迭代中每次对可靠的符号度量值加1,最后采用大数判决的方法来确定译码符号,其属可靠性度量的译码算法。同年,赵大源提出了大数逻辑可译多进制LDPC码的低复杂度译码算法[9],该算法采用星座图上的欧氏距离作为初始化度量值,其只适用于大数逻辑可译码。Chao-Yu Chen提出了多进制LDPC码基于软可靠性度量和硬可靠性度量的译码算法[10],两者采用不同的初始化信息,不适用于高阶调制,只适用于二进制相移键控(Binary Phase Shift Keying,BPSK)调制。
本文提出了一种新的具备翻转规则的多进制LDPC码符号翻转译码算法,当决定某一符号需要翻转时,可以根据翻转规则中的翻转顺序进行翻转。采用具备翻转规则的加权符号翻转算法虽牺牲了一定的性能,但却降低了译码复杂度,在误码性能和复杂度上找到了权衡点,使多进制LDPC码在更低的复杂度上实现了较好的性能。
1 一种符号翻转译码算法
1.1 基本定义
考虑多进制(N,K)LDPC码,其中N为码字长度,K为信息位长度。LDPC码可以完全由稀疏的多进制奇偶校验矩阵H来决定,其校验矩阵H有N列和M≥N-K行。对其任意尝试的符号硬判决向量y,其伴随式向量为s=yHT,其中所涉及的乘法和加法运算都是在GF(q)下进行的。校验矩阵H的行重为dc,列重为dv。定义N(m)表示参与第m个校验方程的dc个符号集合,M(n)表示参与符号n的dv个校验集合:
N(m)={n:hm,n≠0},M(n)={m:hm,n≠0}
(1)
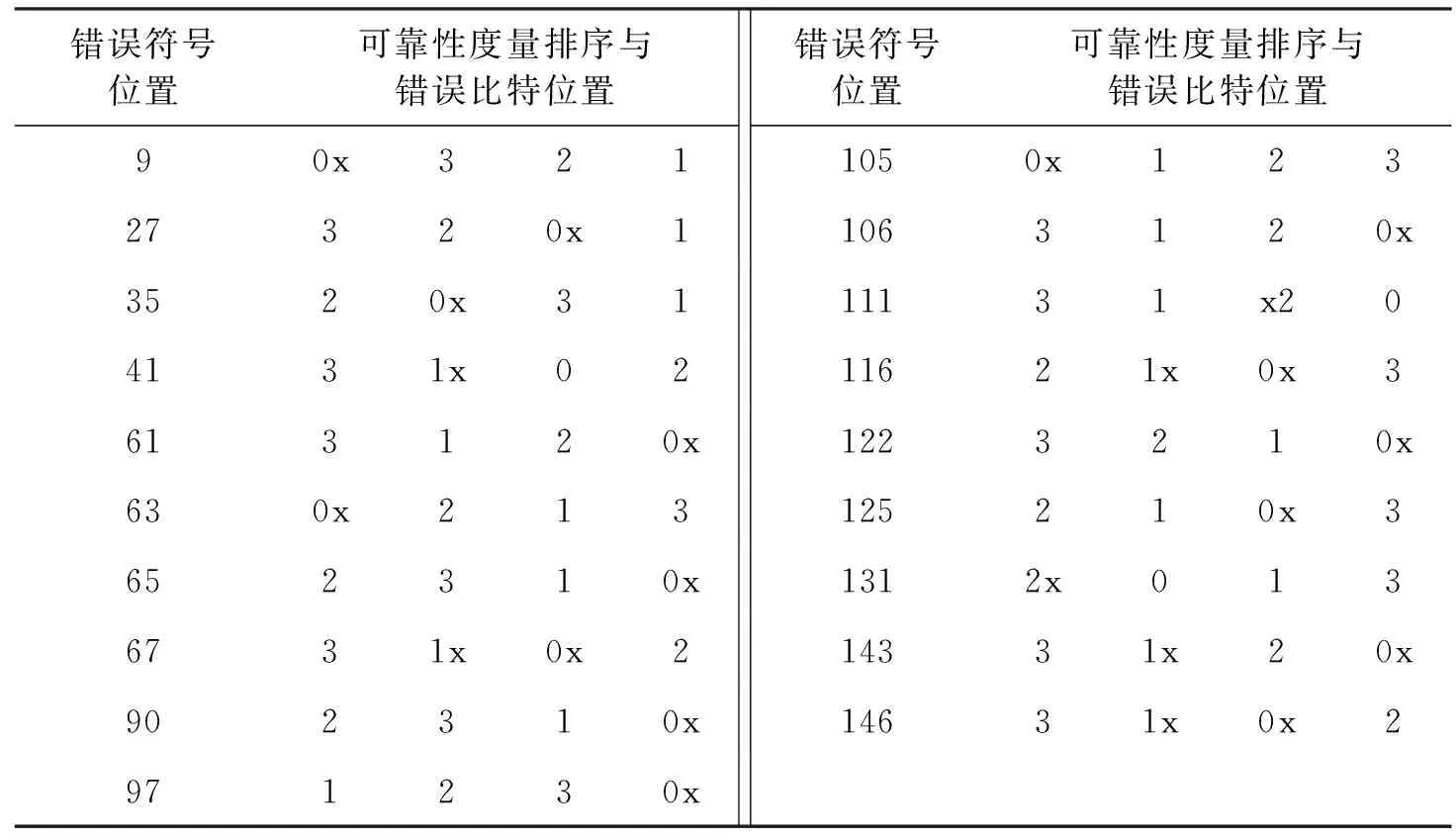
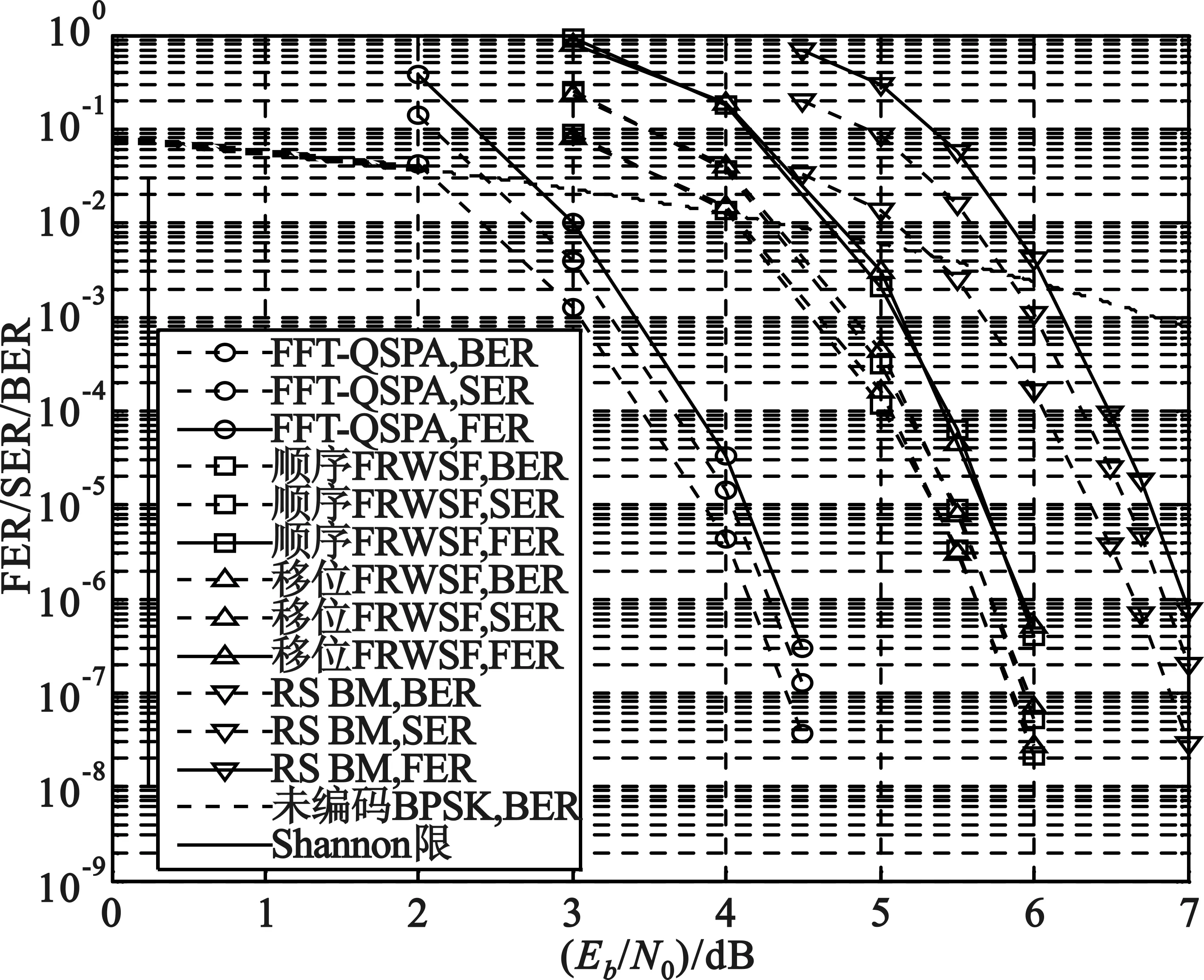
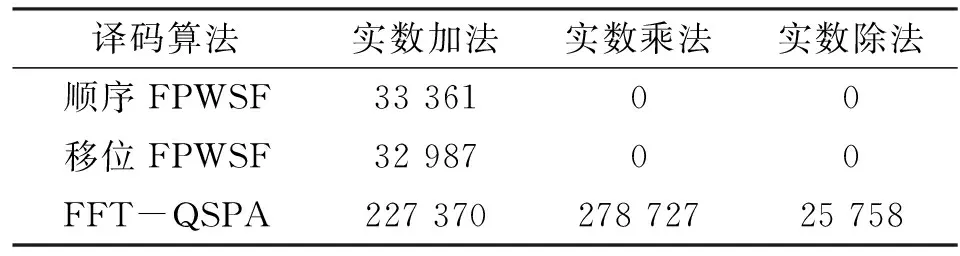
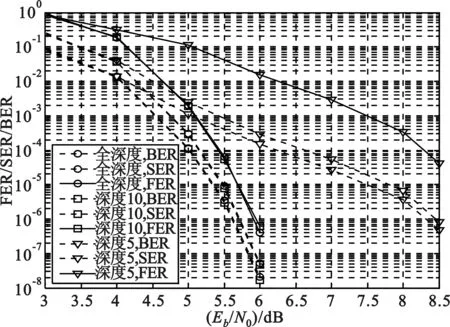
选取任一码字c=[c1,c2,…,cN]∈{GF(q)}N,其中q=2b,在发送之前将码字按发送信号星座图Ω映射成双极性向量t=[t1,t2,…,tN-1],其中tn=[tnb,…,t(n+1)b-1],0≤n 对于0≤i 定义GF(q)域非零元素a的对数似然比: Ln(a)=[Ln(a=α1),…,Ln(a=αq-1)], (2) 式中: (3) 式中,P(a=αi)表示a取值为αi的概率。 定义GF0(q)={α1,…,αq-1}为不含零元的伽罗华域。为了便于表示,第n个符号取值为a的概率向量为Ln=[Ln,α1,…,Ln,a,…,Ln,αq-1],其中Ln,a=∑j:ψ(a)j=+1rnb+j,a∈GF0(q)。可以看出,Ln,a是除去常数项2/σ2的Ln(a=αi)的一种表达形式。 1.2 算法描述 (4) 利用式(4)迭代可计算出E(k-1),E(k-2),…,E(0),如果其中任意一个向量为全零,检测到环路,则当前选择要翻转的符号值就剔除。 算法开始于接收的硬判决向量y(0),在k(k≥1)次迭代之前,符号向量为y(k-1),对应的伴随式向量为s(k-1)=y(k-1)HT≠0。先计算GF0(q)上的决定翻转符号位置的符号度量值,对于每一个符号和每一个GF0(q)的元素, (5) 为估计出符号的可靠性度量,计算出每一个符号的度量值: (6) 根据翻转规则翻转y(k-1)中的符号: y(k)=y(k-1)⊕en(k) (8) 表1 GF(16)下两种不同翻转规则 翻转深度定义为翻转集合中前若干个GF(q)域中的元素。当翻转规则确定之后,其翻转深度可取的范围是1到q。翻转的深度越小,其复杂度就越低,该复杂度的降低是以翻转深度所决定的或大或小的纠错性能损失为代价的。综上所述,在翻转规则中,变量Q是以1为初始值的位置信息,翻转深度为q′≤q,其地址范围为一个模q′计数器。 综上所述,提出的具有翻转规则的译码算法FRWSF如下: 步骤(1) 初始化:设置迭代计数器k=0;计算y(0),Ln和wn,m,a;排除符号列表B←Ø;翻转计数器Q=1。 步骤(3)k←k+1;如果k>kmax(kmax为设定的最大迭代次数),译码失败并停止译码。 步骤(6) 对于选出的翻转符号,根据由Q得到的翻转规则翻转成另一个符号。 步骤(7) 根据式(4)计算E(l),l=k-1,k-2,…,0;如果对于任意l=k-1,…,0,E(l)=0,则如果Q≠q,Q←Q+1,返回到步骤(6);如果Q=q,B←B∪{n(k)}并且Q=1,返回到步骤(5)。 步骤8 根据式(7)计算y(k);B←Ø;返回步骤(2)。 以SNR作为变量来衡量LDPC码的译码性能,我们将研究以下译码算法的误比特率(Bit-ErrorRate,BER)、误符号率(Symbol-ErrorRate,SER)和误帧率(Frame-ErrorRate,FER):(1)FRWSF算法;(2)FFT-QSPA;(3)RSBM算法。 如图1所示,对(150, 76) 16进制的有限域(FiniteField,FF)LDPC码[11]进行了研究,其码率为0.506 7,校验矩阵H是一个行重列重都为9的150×150循环阵,α=1。该码采用顺序和移位翻转规则译码算法(200次迭代)的纠错性能如图1所示。为了便于比较,也给出了LDPC码的FFT-QSPA(200次迭代)和RS码的BM算法的误码性能。 为更好地理解和表述译码算法,以16-ary(150,76)FFLDPC码为例,并选择发送全零的信息符号向量。一个长度为76的全零信息符号经过编码器后得到长度为150的全零码字,码字经BPSK调制并经AWGN信道,经过硬判决,接收到由150个符号组成的码字向量为c=[0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 4 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 8 0 1 0 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 8 1 0 0 0 0 4 0 0 0 0 6 0 0 0 0 0 1 0 0 2 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 0 5 0 0 6 0 0 0]。从接收到的硬判决向量来看,由于已知发送序列,我们知道错误出现的位置和数值,但是对于译码程序来说,这些信息都是未知的。表2给出了存在错误的符号位置以及符号中对应发生错误的比特和度量值大小的排序。以第67个错误符号(向量c中粗体符号位置)为例,[3 1x0x2]中的0、1、2、3表示符号中比特的可靠性程度,0表示的是4个比特当中最不可靠的比特,3表示的是最可靠的比特,符号“x”表示导致符号发生错误的比特,但这对于译码来说是未知的。当传输符号0(0000)时,该位置接收到的硬判决值为6(0110)。FRWSF译码中每次迭代只翻转一个符号,翻转的值是由翻转函数、接收比特软信息和翻转规则等共同决定,表3给出了译码过程中的部分迭代符号翻转过程,其中粗体表示的是每次迭代确定出的翻转符号位置和取值。 表2 错误符号位置及相应比特状态 表3 符号翻转译码的部分迭代过程 如图1所示,顺序翻转规则和移位翻转规则的FRWSF算法的误码性能相差无几,这是因为码字都是在AWGN这一类型的信道条件下传输的。不同翻转规则的译码算法可以应用到不同类型的信道上,可以获取不同的误码性能。特别是在突发信道条件下,翻转规则可以根据突发噪声的特性进行合理设计。在FER为10-5处,与GF(27)域上采用BM算法同比特长度的(86,44) RS码进行比较,FRWSF取得了1.07 dB左右的编码增益。在FER为10-5处,与FFT-QSPA译码进行比较,FRWSF距离FFT-QSPA译码大约1.56 dB。在5.5 dB时采用两种不同的翻转规则对该码进行译码的计算复杂度如表4所示,从表3可以看出,FFT-QSPA实数加法的计算量大约是FRWSF算法实数加法的7倍,并且FRWSF算法不需要实数乘法和实数除法,所以,FRWSF算法的整体计算复杂度比FFT-QSPA低很多。 图1 16-ary (150,76) FF LDPC码和GF(27)域 译码算法实数加法实数乘法实数除法顺序FPWSF3336100移位FPWSF3298700FFT-QSPA22737027872725758 如图2所示,考虑对上述码字采用不同翻转深度的译码算法。从图2中可以看出,具有全翻转深度和深度为10的译码算法误码性能相差不多,但是深度为10的算法复杂度略比全翻转深度的低一些。相对于高深度(如深度为10)而言,翻转深度为5的译码算法以误码性能为代价降低了计算复杂度。因此,在实际应用中翻转深度可以选择略低于伽罗华域阶数q的一个数值来取得一定的权衡。 图2 不同翻转深度的16-ary (150,76) LDPC码的误码性能 本文提出了一种翻转规则的多进制LDPC码加权符号翻转译码算法,在译码过程中,根据每次迭代的翻转函数和翻转深度来选择和翻转码字中的一个符号。算法中具有最小计算开销的环路检测方法不仅有利于翻转符号的选取,也有利于防止在正确码字搜寻过程中陷入到无限环路之中。算法不需要信号的幅度和噪声功率等先验知识,翻转的顺序和深度的选择也带来了较大的灵活性。通过仿真结果和复杂度分析,在相对低伽罗华域下相比于RS码,该算法在中长帧LDPC码上取得了明显的编码增益,而其计算复杂度也较低。所以,提出的译码算法取得了很好的纠错性能和复杂程度上的权衡。 [1] Gallager R G. Low-Density Parity-Check Codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21-28. [2] Chung S Y, Forney G D, Richardson T J, et al. On the Design of Low-Density Parity-Check Codes within 0.0045 dB of the Shannon Limit[J]. IEEE Communications Letters, 2001, 5(2): 58-60. [3] 张誉,雷菁,文磊. 多进制LDPC译码算法的研究[J]. 通信技术,2011, 44(05): 21-23. ZHANG Yu, LEI Jing, WEN Lei. Research on Nonbinary LDPC Decoding Algorithm[J]. Communications Technology, 2011, 44(05): 21-23. [4] Davey M C, Mackay D. Low-Density Parity Check Codes over GF(q)[J]. IEEE Communications Letters, 1998, 2(6): 165-167. [5] Mackay D, Davey M. Evaluation of Gallager Codes for Short Block Length and High Rate Applications[C]. Proc. IMA International Conf. Mathematics its Application: Codes, Systems and Graphical Models. New York, 2000: 113-130. [6] Declercq D, Fossorier M. Decoding Algorithms for Nonbinary LDPC Codes over GF(q)[J]. IEEE Transcations on Communications, 2007, 55(4): 633-643. [7] ZHAO S, LU Z, MA X, et al. A Variant of the EMS Decoding Algorithm for Nonbinary LDPC Codes[J]. IEEE Communications Letters, 2013, 17(8): 1640-1643. [8] CHEN C, BAI B, WANG X, et al. Nonbinary LDPC Codes Constructed based on a Cyclic MDS Code and a Low-Complexity Nonbinary Message-Passing Decoding Algorithm[J]. IEEE Communications Letters, 2010, 14(3): 239-241. [9] ZHAO D, MA X, CHEN C, et al. A Low Complexity Decoding Agorithm for Majority-Logic Decodable Nonbinary LDPC Codes[J]. IEEE Communications Letters, 2010, 14(11): 1062-1064. [10] CHEN C, HUANG Q, CHAO C, et al. Two Low-Complexity Reliability-based Message-Passing Algorithms for Decoding Non-Binary LDPC Codes[J]. IEEE Transcations on Communications, 2010,58(11):3140-3147. [11] SONG S, ZHOU B, LIN S, et al. A Unified Approach to the Construction of Binary and Nonbinary Quasi-Cyclic LDPC Codes based on Finite Fields[J]. IEEE Transcations on Communications,2009,57(1):84-93. Weighted Symbol-Flipping Decoding Algorithm for Nonbinary LDPC Codes ZHANG Yong-yu (Unit 91469 of PLA, Beijing 100841, China) A low-complexity symbol-flipping algorithm for nonbinary LDPC (Low-Density Parity-Check) codes based on flipping rules is proposed. In searching of valid codeword, the proposed algorithm iteratively updates the received symbol vector of hard-decision in symbol vector space. Only one symbol is flipped in each iteration, and symbol flipping function comprehensively considers the number of failed checks and the reliability of the received bits and calculated symbols. A scheme to avoid infinite loops and select flipping symbol in high-order Galois field is adopted and meanwhile, the design of flipping rules is also proposed, which determines the computational complexity and error performance. Simulation results indicate that this algorithm could achieve an effective tradeoff of between error-correcting performance and computational complexity for the 16-ary (150,76) LDPC code. nonbinary; LDPC codes; iterative decoding; flipping rule 10.3969/j.issn.1002-0802.2015.11.004 2015-06-08; 2015-09-28 Received date:2015-06-08;Revised date:2015-09-28 TN911.22 A 1002-0802(2015)11-1222-06 张用宇(1977—),男,硕士,高级工程师,主要研究方向为无线通信系统。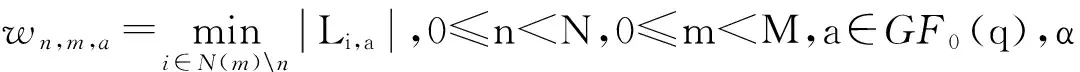
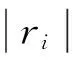
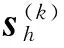
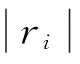
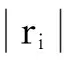

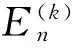
2 仿真结果

3 结 语
