无线传感器网络中不同节点分布模型的性能分析*

2015-03-25周智勇王海涛

通信技术 2015年11期

关键词：次方均匀分布覆盖率

周智勇，陈晖，王海涛

(1. 解放军理工大学通信工程学院研三队,江苏南京 210007；2. 解放军理工大学训练部, 江苏南京 210007)

无线传感器网络中不同节点分布模型的性能分析*

周智勇1，陈晖2，王海涛2

(1. 解放军理工大学通信工程学院研三队,江苏南京 210007；2. 解放军理工大学训练部, 江苏南京 210007)

针对传感器网络中较为关心的生存时间和覆盖率问题，对不同分布模型下的网络性能进行了分析。根据传感器网络中节点密度的分布规律，基于传统的分簇LEACH协议，选择对均匀分布、一次衰落和0.5方衰落三种随机分布场景下传感器网络的生存时间、覆盖率等指标进行了研究，仿真实验表明：对于三种传感器节点的撒布模型：一次衰落模型网络生存时间最长，但覆盖率最低；均匀分布网络生存时间最短，覆盖率最高；0.5次衰落模型下两项性能折中，更加符合现实需求。

网络生存时间；覆盖率；节点分布模型；性能分析

0 引言

当前无线传感器网络(WSNs)技术迅猛发展，其在目标监控、物联网、战场信息收集和工业等领域有着广泛的应用前景[1]。如图1，无线传感器网络由分布在一定区域内的大量传感器节点和收集所有节点信息的汇聚节点Sink组成。传感器节点通常由自身携带的电池供电，而在大多数情况下，电池携带能量有限且不能再次充电，因而降低传感器网络中的能量消耗成为当前对于传感器网络研究的重点问题，也是制约传感器网络应用的瓶颈之一。

降低无线传感器网络的能耗的方法有很多种，如在网络层方面，文献[2]提出通过合理规划选路协议提升传感器网络的能量利用效率，文献[3]引入空闲节点休眠机制，使处于不工作状态的节点及时转变为休眠状态，减少传感器网络中节点的待机能耗；在物理层方面，人们提出了一些能够降低单位比特传输能量的新技术[4-5]。文献[6-7]研究了合理选择节点分布模型对于提升网络生存时间的作用，并且针对节点能耗不均衡的问题提出了各自的解决方案，但是这些研究都是基于确定性的节点分布模型，并不适用于很多实际的应用场景。

图1 无线传感器网络的结构

针对随机分布下的传感器网络，文献[8]总结了几种常用的分布模型，并对它们的网络性能进行了初步的分析和比较，但其只是得到了提高Sink节点附近的节点密度可以提升网络生存时间的结论，没有进一步量化分析。此后，文献[9]提出了一种随机分布下的同心环几何模型，该模型以Sink节点为中心，由外向里的各环节点密度呈几何级增加，从而克服汇聚节点周围通信负荷过大的问题。然而这一方案并没有考虑覆盖率的问题，区域内存在大量的冗余节点，很容易造成资源的浪费。为了提高能量效率，文献[10]给出了一种基于贪心算法的节点随机分布方案，旨在利用尽量少的节点实现同样的网络生存时间和覆盖性能，但是与之前的大多数研究一样，该方案只是建立在平面路由协议的基础上，并没有考虑引入层次路由协议，而后者的性能显然更加优异，应用也更为广泛。

因此，本文着重讨论了分簇LEACH协议下的几种典型的随机分布模型，并对它们的网络生存时间和覆盖性能进行了深入的分析和对比，具体的工作和章节安排如下所示：

(1)第二部分在接力传输方式下对传感器网络的能耗进行系统描述和公式建模，对不同的节点撒布模型进行公式和实例描述；

(2)第三部分针对网络生存时间和覆盖率两项性能进行了仿真，并给出了各个分布模型的对比性能分析。

(3)第四部分对实验结果和本文的主要工作进行总结。

1 系统描述和公式建模

1.1 通信模型

传感器网络采用传统的LEACH分簇路由协议[11]。设定我们需要监控的区域为二维区域A为以汇聚节点Sink(0,0)为圆心，半径为y=250 m的圆形区域。监控目标D在区域A内随机出现。当监控目标D在传感器节点m的感知距离内时，传感器节点m生成可以传输的信息。根据LEACH协议，所有能够探测到目标D的传感器节点把信息传输到各自簇头处。簇头将收集到的信息通过能耗最低的路径接力传输到汇聚节点Sink处。

1.2 节点分布模型

在真实应用条件下，传感器的投放通常使用空投等手段，而由于风速、传感器外观特征等条件的影响，传感器节点的具体位置必然呈现某些随性特征。本文中主要考虑一次衰落分布、均匀分布、0.5次方衰落分布条件下的分布特性：

(1)一次衰落分布模型

在需要监控的区域A内，一次衰落分布模型的传感器位置的概率密度函数表示为：

(1)

其中r表示到汇聚节点Sink的距离，通过合理调整参数a使得概率密度函数f(r)在0～250 m积分为1。若x在0～250 m内满足均匀分布，则通过一定的变换r=T(x)可以使得变量r的概率密度满足(1)式。对于变换关系r=T(x)，则有：

(2)

化简可得变换关系r=T(x)：

(3)

一次衰落分布的具体场景如图2所示。

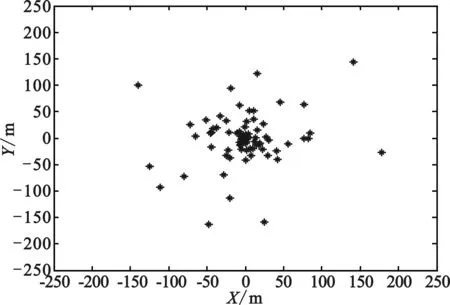
图2 一次衰落分布

(2)均匀分布模型

在文献[8]中提出了在极坐标下的均匀分布，即在极坐标下两个变量(r,θ)分别满足均匀分布，联合概率密度函数为：

(4)

其中R表示变量r的最大值。本文中极坐标条件下的均匀分布如图3所示。

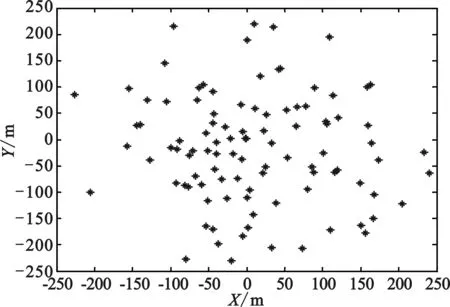
图3 均匀分布

(3)0.5次方衰落分布

在需要监控的区域A内，0.5次方衰落分布模型的传感器位置的概率密度函数表示为：

(5)

其中r表示到汇聚节点Sink的距离，通过合理调整参数a使得概率密度函数f(r)在0～250 m积分为1。同样根据式(2)，有变换关系r=T(x)：

(6)

化简可得变换关系r=T(x):

(7)

0.5次方衰落分布的具体场景如图4所示。

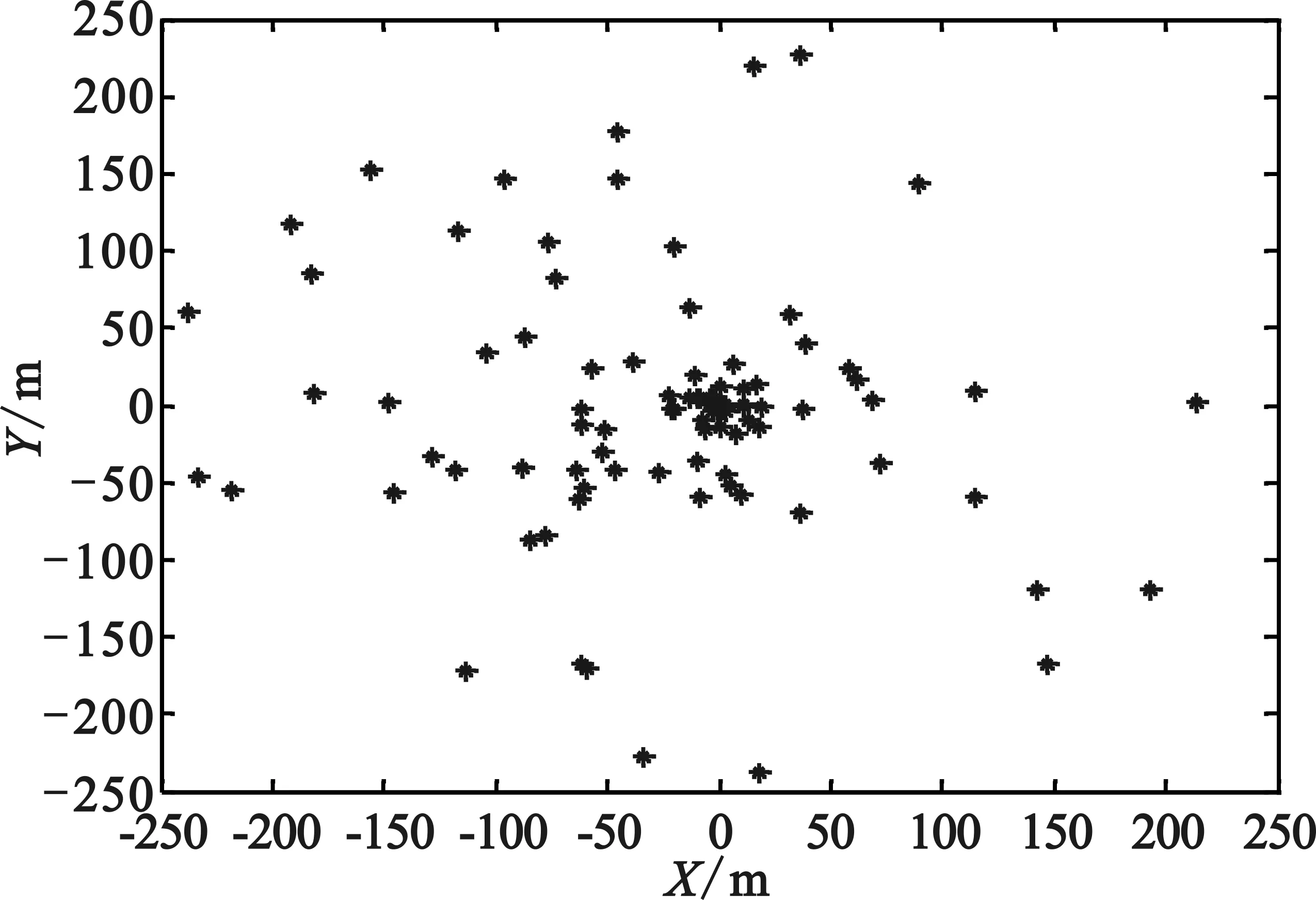
图4 0.5次方衰落分布

(4)三种分布特性的关系

在极坐标条件下，三种分布的概率密度函数如图5所示。

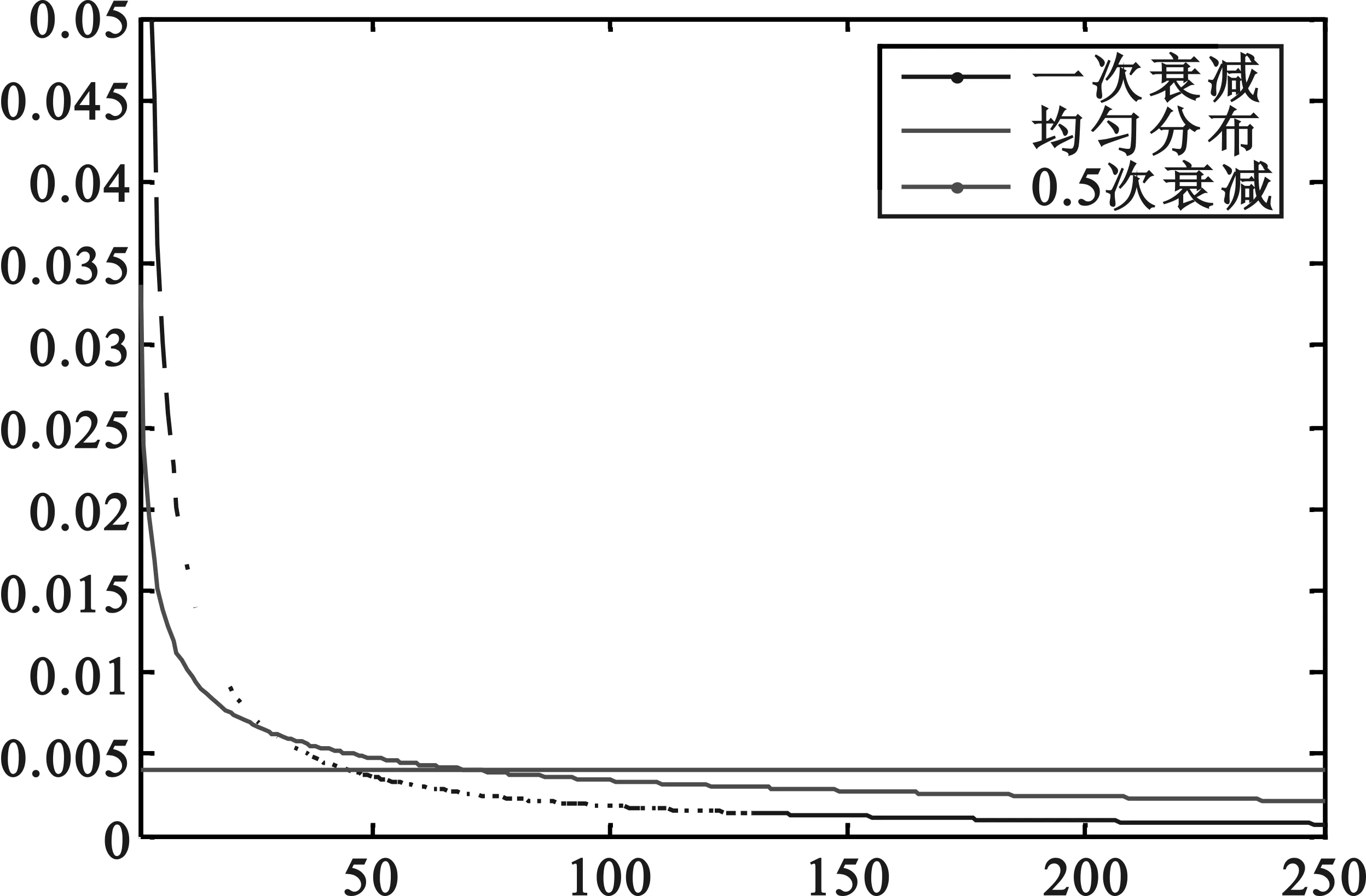
图5 三种不同分布的对比

从图5中可以看出，在靠近Sink点处，节点分布密度一次衰减>0.5次衰减>均匀分布，相反在远离Sink点处，均匀分布>0.5次衰减>一次衰减。

1.3 能耗模型

本文中点对点通信采用QPSK方式，根据文献[12]，点对点QPSK方式的误码率特性为：

(8)

bQPSK=sin2(π/4)

(9)

其中ρ表示接收端信噪比。若通信需要的最低误码率要求为ΨQPSK≤ρrequire时，通过查表的方式可以逆向得到最低接收信噪比为ρ0。发送功率与接收端信噪比满足路径损耗方程：

(10)

其中P、N0分别为发送功率、噪声功率，h为衰落信道的衰落系数，d为发送端和接收端的距离，α为路径损耗系数，Gt、Gr分别为发送和接收天线增益。当ρ=ρ0时，可以计算出发送端需要的发送功率：

(11)

1.4 网络生存时间

文献[4，5，8]对网络生存时间进行了不同的定义，其中文献[4-5]将网络生存时间定义为从网络开始运行到出现能量耗尽的节点时所经历的时间，而文献[8]将网络生存时间定义为从网络开始运行到网络对监控目标区域的覆盖率下降到容忍值的时间。本文采取前一种的定义方式，这是因为一旦网络中出现死亡节点，死亡节点周边其他传感器节点的能耗急剧增加，导致其他的传感器节点很快耗尽电池的能量。能够有效推迟第一个节点的死亡时间的节点分布模型具有很大可能能够推迟大部分节点的死亡。

2 仿真与数据分析

本文设定监控区域为二维区域A为以汇聚节点Sink(0,0)为圆心，半径为y=250 m的圆形区域。需要监控的目标随机出现在区域A内，且目标的分布满足均匀分布。区域A内传感器总数为100个。由于节点的分布和目标出现的位置均具有较大的随机性，因而本文对每种情景进行了5次仿真。其他仿真参数的设置如表1所示。

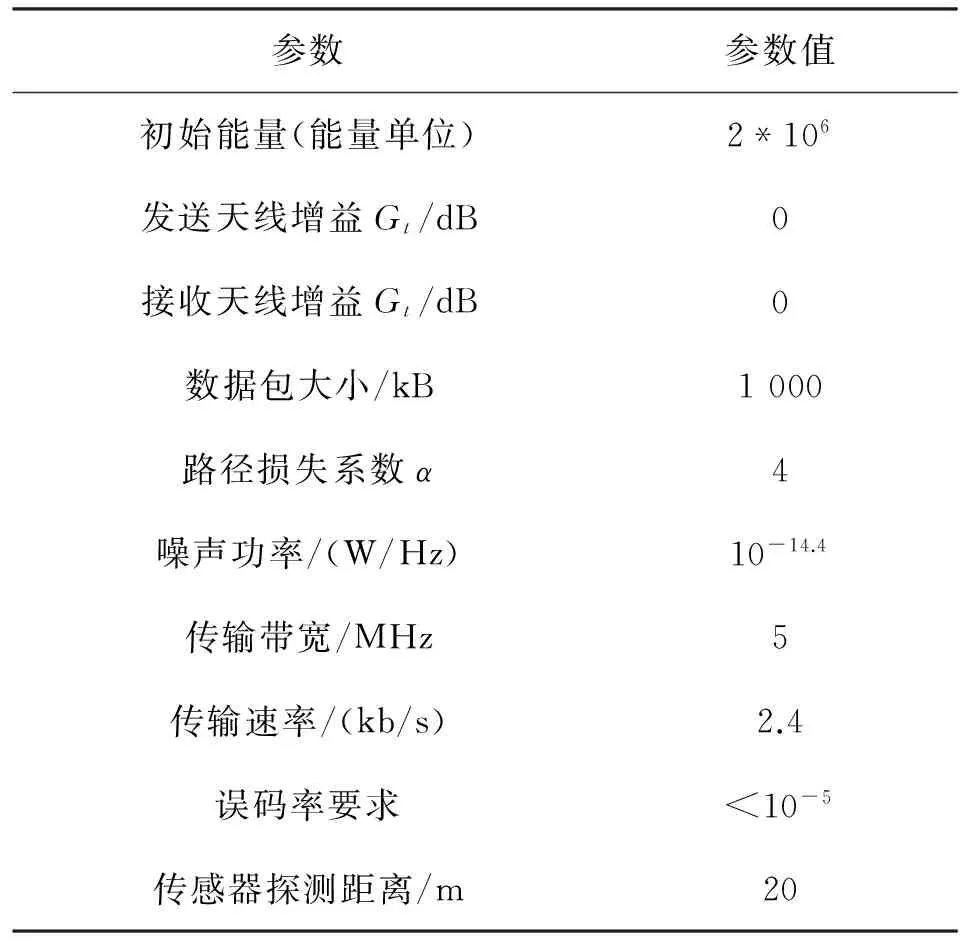
表1 仿真参数设置

图6展示了在三种不同的传感器分布模型下网络的生存时间。当传感器采用一次衰落分布模型时，传感器网络的生存时间最长，其次是0.5次衰落分布模型，均匀分布的网络生存时间最短。这是因为在传感器网络中，接近汇聚节点Sink的节点在接力通信和协同通信中承担更多的中继任务，因而这些节点电池消耗更大，在一次衰落分布模型中(如图3)靠近汇聚节点Sink点的节点分布密度更大，可以分担由于中继产生的能量消耗。Sink节点附近的节点密度：一次衰减>0.5次衰减>均匀分布，因而不同分布模型下网络的生存时间：一次衰减>0.5次衰减>均匀分布。

图6 不同节点分布模型下网络生存时间的比较

从图7中可以看出，不同分布模型的覆盖率：均匀分布优于0.5次方衰落分布，而0.5次方衰落分布优于一次方衰落分布。这是因为一次方衰落分布传感器节点较多分布在汇聚节点Sink点周围，在区域A边缘分布的节点密度较小，因而对于出现在区域A边缘的目标探测能力不足；均匀分布在整个区域A内节点密度相同，因而对所有位置目标的探测能力相同，覆盖率最高；0.5次方的分布特征介于其他两种分布之间，因而覆盖率性能介于两者中间。

图7 不同节点分布模型下网络覆盖率的比较

图8进一步展示了在网络达到网络生存时间后，即出现第一个节点死亡后，网络覆盖率随时间变化情况。仿真中每隔100000轮进行网络覆盖率的测算，由于仿真采用蒙特卡洛方法，因而曲线呈现略微的抖动。从图中可以看出，采用均匀分布模型时，网络的初始覆盖率最高，0.5次衰减次之，一次衰减的初始覆盖率最低。由之前的讨论得知，这是由不同分布的节点集中情况决定的。当网络中不断出现节点死亡后，三种分布的覆盖率均会下降。均匀分布模型覆盖率下降最快，0.5次衰减次之，一次衰减的覆盖率下降最慢。这是因为一次衰减节点分布较为密集，不同节点重复覆盖的区域较多，因而当出现节点死亡时网络的覆盖区域不会出现较大的变化。相反，均匀分布的节点分布较为均匀，网络不同节点重复覆盖的区域较少，因而单个节点死亡对于网络覆盖率的影响较明显。0.5次次衰减分布则具有较好的折中性能。

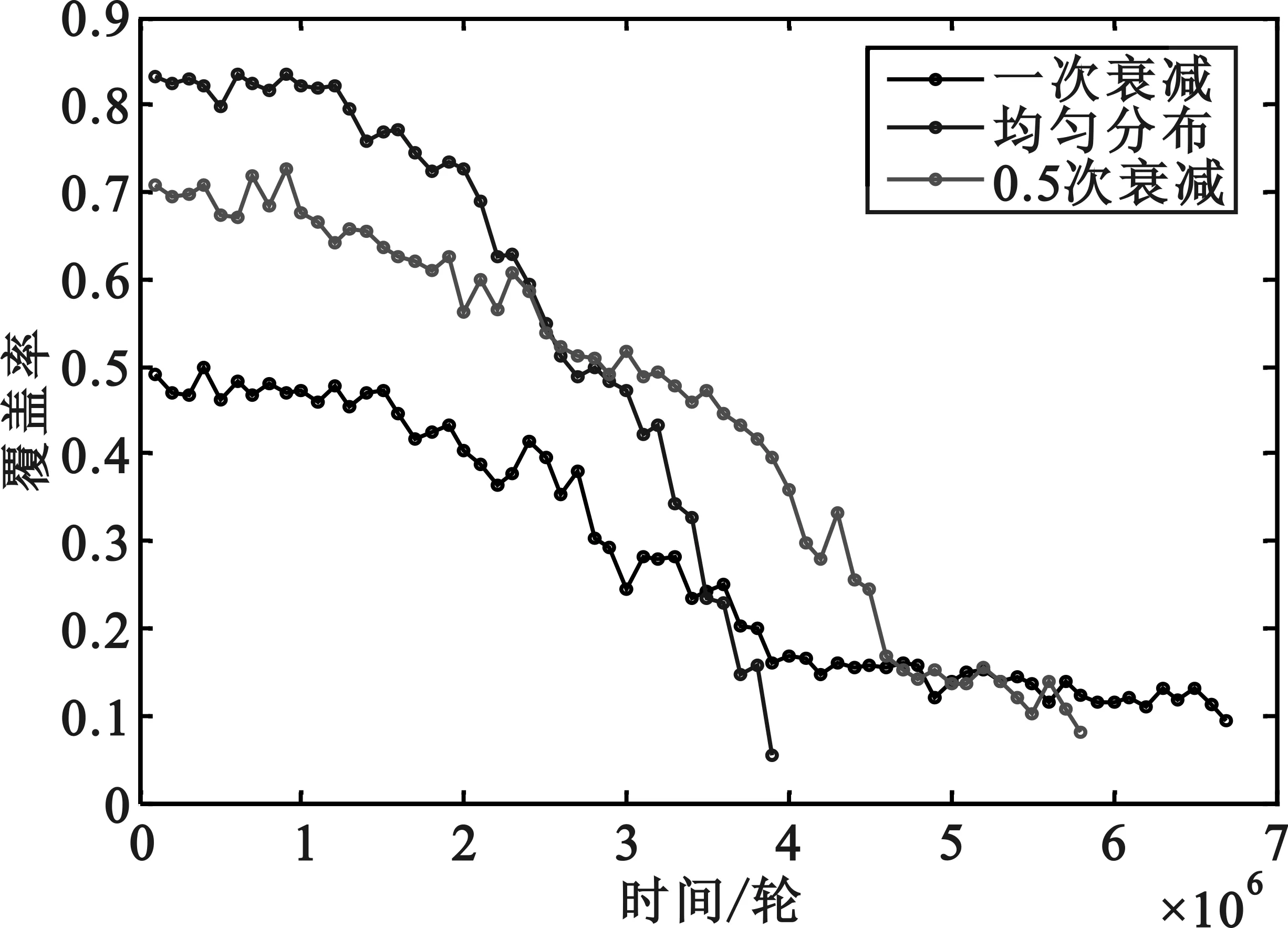
图8 不同节点分布模型下网络覆盖率随时间变化的比较

3 结语

本文针对传感器网络中较为关心的提升能量利用效率和网络生存时间问题。结合传统LEACH协议对于几种常见的传感器分布模型进行了能耗、覆盖率率等性能仿真实验。比较一次衰减、0.5次方衰减和均匀分布三种网络节点分布模型，一次衰减分布能够实现最大网络生存时间，但同时覆盖率最差；均匀分布网络生存时间最小，但覆盖率最优；0.5次衰减模型的两项指标性能介于前两种方式之间，能够实现性能的折衷。

[1] Akyildiz I F, SU W, Sankarasubramaniam Y, et al. A Survey on Sensor Networks[J]. IEEE Communications Magazine, 2002, 40(8):102-114.

[2] CHANG R Y, CHUANG W H. Best-First Tree Search with Probabilistic Node Ordering for MIMO Detection: Generalization and Performance-Complexity Tradeoff[J]. IEEE Transactions on Wireless Communications, 2012, 11(2):780-789.

[3] Fiems D, Andreev S, Demoor T, et al. Analytic Evaluation of Power Saving in Cooperative Communication[C]// Conference on Future Internet Communications (CFIC). Coimbra: IEEE Press, 2013:1-9.

[4] CHENG P, Chuah C N, LIU X. Energy-Aware Node Placement in Wireless Sensor Networks[C]// Global Telecommunications Conference, Dallas: IEEE Press, 2004:3210-3214 Vol.5.

[5] ZHANG J, SONG C, Sharif H, et al. A Battery-Aware Deployment Scheme for Cooperative Wireless Sensor Networks[C]// Global Telecommunications Conference, 2009. Honolulu: IEEE Press, 2009:1-5.

[6] REN L, GUO Z, MA R. Distance-based Energy Efficient Placement in Wireless Sensor Networks[C]. IEEE Conference on Industrial Electronics and Applications. Singapore: IEEE Press,2008:2031-2035.

[7] 金帅，王琪，吴义魁等. 高斯分布下的 WSN 能量均衡算法[J]. 通信技术, 2011,44(06):110-113. JIN Shuai， WANG Qi， WU Yi-kui，et al.Balanced Energy Algorithm for Wireless Sensor Network based on Gaussian Distributed[J]. Communications Technology, 2011, 44(06):110-113.

[8] Ishizuka M, Aida M. Performance Study of Node Placement in Sensor Networks[C]// Proceedings of the 24th International Conference on Distributed Computing Systems Workshops, Washington, DC: IEEE Press, 2004: 598-603.

[9] Chatterjee P, Das N. Distributed Data Gathering with Graded Node Distribution in Sensor Networks to Maximize Lifetime[C]// IEEE International Conference on Advanced Information Networking & Applications, Singapore: IEEE Press, 2011:435-442.

[10] Chatterjee P, Das N. Coverage Constrained Non-Uniform Node Deployment in Wireless Sensor Networks for Load Balancing[C]// Applications and Innovations in Mobile Computing (AIMoC), Kolkata: IEEE Press, 2014:126-132.

[11] Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks[C]// Proceedings of the 33rd Hawaii International Conference on System Sciences, Hawaii: IEEE Press, 2000:8020.

[12] LIU R. Cooperative Communications and Networking (LIU, K.J.R. et al) [Book Review][J]. Signal Processing Magazine IEEE, 2009, 26(5):149-150.

Performance Analysis of Different Nodes Distribution Models in Wireless Sensor Networks

ZHOU Zhi-yong1，CHEN Hui2，WANG Hai-tao3

(1.Institute of Communications Engineering, PLAUST, Nanjing Jiangsu 210007, China；2.Department ofTraining, PLAUST, Nanjing Jiangsu 210007, China )

Aiming at the commonly-concerned issue of lifetime and coverage ratio in WSNs, network performance in different distribution models is analyzed.In accordance with the distribution regularities of node density in WSNs and based on the traditional cluster LEACH protocol,the lifetime and coverage ratio of WSNs is discussed under three random distribution scenarios of first-order fading distribution, uniform distribution and 0.5 order fading distribution. Simulation experiment indicates that in the three different distribution models, the first-order fading distribution is the best in extending network lifetime but the lowest in coverage ratio,while the uniform distribution performs on the contrary; 0.5 order fading distribution strikes a trade-off in these two performances, thus more suitable for practical demand.

network lifetime; coverage ratio; nodes distribution model; performance analysis

10.3969/j.issn.1002-0802.2015.11.013

2015-06-06；

2015-09-20 Received date:2015-06-06；Revised date：2015-09-20

TP393

1002-0802(2015)11-1270-05