声光式激光外差振动测量系统研制与实验研究

刘 建，冯国英，谷晓彬，罗 韵，周寿桓，2

(1.四川大学电子信息学院，四川 成都610065;2.华北光电技术研究所，北京100015)

1 引言

激光外差振动测量技术是一种基于多普勒效应的激光相干探测手段，具有非接触、灵敏度高、作用距离远等众多的优点，在科研与工业应用领域中具有广泛的应用［1－4］，如水下声光通信［5－6］、微弱超声振动信号检测［7］、爆炸冲击测量［8］、语音信号实时获取与复原［9］、固体发动机振动测量［10－11］、耦合振动检测［12］、车辆识别［13］、微纳结构体振动测量［14］、声致振动检测［15］、电子器件表面振动测量［16］等。在激光外差干涉系统中，需要在参考光或者信号光中引入一定的频率偏移量，使得两光束之间存在一个频率差，从而在探测器光敏面处发生混频干涉后形成一个中频信号作为载波［3－4］。常用的频移引入方法有波片旋转法［17］、双频激光器法［18］以及声光调制器法［19］等。其中，声光移频法基于声光效应，具有衍射效率高、频移量可调、性能稳定等特点［20－21］。基于此，设计并搭建了基于声光移频式激光外差多普勒振动测量系统，并对该系统对于振动源振幅和频率变化的响应做了验证性实验，最后探究了其在小型旋转机械故障监测中的应用。

2 声光式外差振动测量系统搭建

2.1 系统设计

本文设计并搭建的声光移频式的光外差振动测量系统，其结构原理图如图1所示，主要由光路、信号处理两部分组成。如图1所示，光路部分由分别作为分束镜和合束镜的分光镜BS1、BS2，偏振分光棱镜PBS，聚焦透镜L1、L2，二分之一波片(633 nm)HWP1、HWP2，高反射率透镜 M，四分之一波片(633 nm)QWP以及声光移频器AOM等组成;信号处理部分主要由放大器、混频器、自动增益控制器(AGC)和锁相环(PLL)等组成。

激光器出射光为线偏振光，频率为f0，经过扩束器扩束准直后在BS1处分为反射光和透射光，分别进入参考光路和信号光路。在参考光路中，光束经HWP1透射、M反射进入AOM发生衍射，输出0级光和1级光，1级光相比于入射光发生80 MHz频移，频率变为f0+fAOM，取该一级光作为参考光。参考光经L1聚焦、BS2反射后落在探测器表面。其中，HWP1被用来调节参考光偏振方向以达到和信号光偏振匹配。在信号光路中，首先，光束经过HWP2后偏振方向发生旋转。设置合理的HWP2角度，使得光束经过PBS时发生完全透射;随后该光束经由QWP照射在振动源表面后反射，该反射光中携带有由振动引入的多普勒频移 fd=2v/λ［3－4］，从而频率变为f0+fd。设置合适的QWP快轴角度，使得反射光二次经过QWP后偏振态发生90°偏转，从而再次经过PBS时发生完全反射，这一设计提高了光能利用率，该反射光作为信号光;最后，信号光经过L2聚焦、BS2透射后落在探测器表面。信号光和参考光在探测器光敏面处发生混频干涉，输出带有振动信息的拍频信号，频率为fd－fAOM，随后该信号进入信号处理部分进行振动信息解调，下面将对该解调过程进行详细描述。

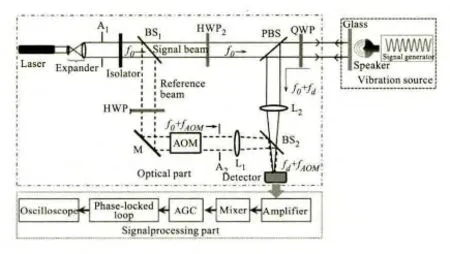
图1 激光外差振动测量系统示意图Fig.1 Schematic diagram of laser heterodyne vibration measurement system

在信号处理部分，利用锁相环对拍频信号进行鉴相处理。相位是频率变化对时间的积分，两者可相互转换，因此我们以相位调制信号来表示拍频信号。假设表面振动位移为u(t)，则此时拍频信号可表示为:

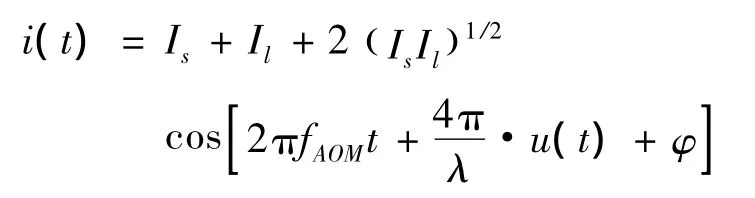
其中，Is和Il分别为信号光和本振光的直流分量;φ为相位差。fAOM=80 MHz，为声光移频器频移量。由式(1)可知，拍频信号为载频为80 MHz的相位调制信号，其振幅与参考光和信号光强度相关。

为了便于后续处理，探测器输出拍频信号经过放大器放大后进行混频降频处理。利用一有源晶振产生84 MHz正弦波作为参考信号，与拍频信号进行混频，取其差频部分，则此时拍频信号载频变为4 MHz;随后，该降频信号进入AGC模块。该模块可使得拍频信号幅值始终保持在一定范围内，从而满足后续PLL解调电路要求;最后，利用PLL进行鉴相处理，输出与拍频信号相位变化成正比的电信号，也即为与u(t)成正比，可表示为:

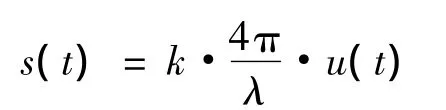
其中，k为一比例常数。这样，通过放大、混频降频、AGC控制、锁相环鉴相即完成了振动信息的解调。

在本系统中，所用光源为He－Ne激光器，型号为 DH－HN250P，中心波长为632.8 nm，功率约为3.2 mW。AOM工作波长为632.8 nm，中心频率为80 MHz。光电探测器选用的是Thorlabs公司型号为PDA10A－EC的硅光电探测器，其波长响应范围为200～1100 nm，带宽为150 MHz。BS1、BS2为5∶5消偏振分光棱镜，PBS为单波长偏振分光棱镜(633 nm)，型号为GCC－4020，消光比大于1000∶1。L1、L2均为焦距为300 mm 的双胶合透镜，可变光阑A1、A2用来调节光斑大小以及滤除杂散光，以提高系统信噪比。隔离器用以隔离系统散射光进入激光器以提高光源稳定性。如图2所示，所用振动源为一扬声器，利用信号发生器对其进行可变振幅、频率驱动。扬声器发出的声音信号作用在玻璃板上产生声致振动，信号光照射在振动玻璃表面即可通过所述系统复原得到振动信息。

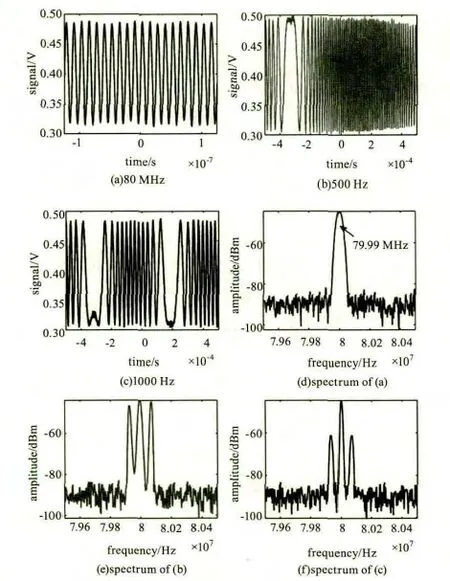
图2 利用所述系统得到的拍频信号Fig.2 Beat signals obtained by the proposed system

2.2 信号获取与解调实验

为了验证所搭建测振系统的可行性，对其进行了可行性验证实验。在外差光路中，信号光和参考光必须保持很高的空间准直性才能获得拍频信号［22－23］。通过仔细的光路调节，获得了拍频信号输出，其波形图和频谱如图2所示。其中，图2(a)为未施加振动时的拍频信号时域波形图，图2(d)为其对应的频谱，其峰值频率为79.99 MHz，与标准中频信号频率80 MHz误差为0.01%。图2(b)、(c)为施加振动信号时的拍频信号波形图，驱动频率分别为500 Hz和1000 Hz，驱动电压均为4 V，图2(e)、图2(f)分别为图2(b)、图2(c)所对应的频谱图。由图2可知，施加振动后拍频信号显示出了明显的振动调制，频谱中产生了新的频率成分，与理论相符合。

在得到拍频信号的基础上，下一步就是从该拍频信号中解调得到振动信息。以500 Hz振动信号为例说明整个的解调过程，如图3所示。图3(a)所示为84 MHz信号波形图，图3(d)为其对应的频谱图，由图3(d)可知，峰值频率为83.998 MHz，与84 MHz相差0.002%。图3(b)和图3(e)为混频信号经过滤波后得到的以4 MHz载波的拍频信号波形图和频谱图。图3(e)和图3(f)分别为锁相环解调输出信号的波形图和频谱图，由图可知，输出信号为一近似正弦波，峰值频率为 499.94 Hz，误差为 0.01%。

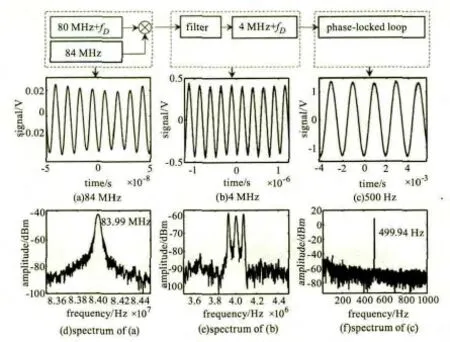
图3 拍频信号解调过程Fig.3 Beat signal demodulation process

3 振动源振幅与频率变化响应度实验研究

在完成了系统搭建以及信号解调的基础上，通过改变振动源的振幅、频率等，对该系统对于频率与振幅变化的响应度进行了验证性实验探究。

3.1 振动源振幅变化

为了验证该系统对于振动源振幅变化的响应度，固定振动源驱动频率为500 Hz，驱动电压由2 V以0.2 V步进到4 V，记录了解调信号的波形图变化，结果如图4所示，插图为驱动电压分别为2.0 V，2.6 V，3.2 V 和 4.0 V 时输出信号波形图的对比图。由图4可知，解调输出信号幅值随着驱动电压的增大而增大，近似为线性，这与驱动电压越大振动振幅越大是相符合的，验证了该系统对于振动振幅变化的响应度。

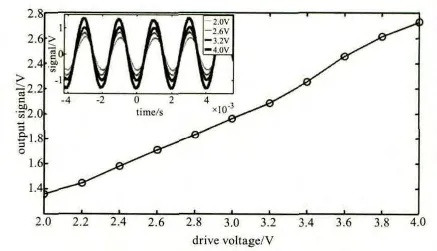
图4 输出信号幅值与驱动电压对应图Fig.4 Diagram of the output signal amplitude vs the driving voltage

3.2 振动源频率变化

为了验证该系统对于振动频率变化的响应度，固定振动源驱动电压为4 V，驱动频率从10 Hz以10 Hz步进到100 Hz，记录解调信号的频谱变化如图5所示。其中，图5(a)为测量得到的各频率频谱对比图，各峰值频率如图中所标示;图5(b)为图5(a)中所得峰值频率与驱动频率的对比图;图5(c)为相对误差曲线，由该曲线可知:在10～100 Hz频段内，测量误差小于0.15%。同样的，对100～1000 Hz，1～10 kHz频段的测量精度进行了测量，相对误差分别小于0.07%、0.03%。由此可知，该系统可对10 Hz～10 kHz振动频率内进行精确的测量，且频率较高时其测量相对误差较小。

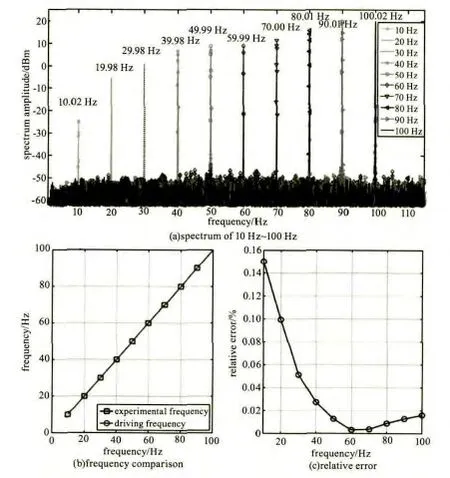
图5 10～100 Hz振动测量结果图Fig.5 The vibration measurement results of 10 ～100 Hz

4 应用举例

旋转机械在现代工业中具有相当广泛的应用，如压缩机、发电机等，利用外差光学方式可实现特殊环境下，如高温、高压等情况下的振动测量。限于实验室条件，我们对一小型旋转设备－空气螺丝起子进行了振动测量。测量部位为压缩机密封盖处。将密封盖处固定螺丝轻微旋转使得密封度下降，即人为引入一机械故障，分别记录了在有、无故障情况下测量点的振动波形图及频谱图，结果如图6所示。图6(a)、(b)分别为无故障、有故障下的波形图，由图可以看到，故障发生后，振动时域图发生明显变化，且峰峰值相对变大;图6(c)、(d)分别为图6(a)、(b)所对应的频谱图，由该图可以看出，未存在故障时，测试点振动频率主要为25 Hz以及谐波成分，如 50 Hz，75 Hz，100 Hz 等;当发生故障时，低频成分基本未变化，在175～250 Hz频段内(左侧虚线框所示)，频谱幅值相对变小;在250～350 Hz频段内(右侧虚线框所示)，产生了新的频谱成分。该实验结果表明，通过监测旋转机械某测试点的频谱变化，可有效地对其运行状况进行监测，可及时地发现故障的出现以避免更大的损失。

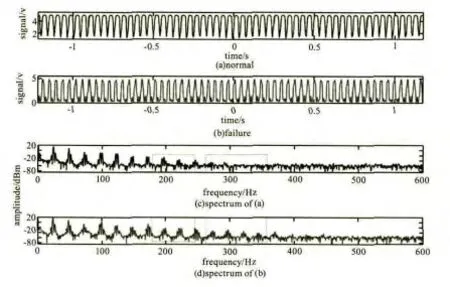
图6 小型旋转机械某测试点Fig.6 The vibration measurement results of a point of small rotating machinery in the condition of normal and fault

5 总结

本文设计并搭建了基于声光移频式的激光外差振动测量系统。首先通过仔细地调整光路，获得了拍频信号输出，并利用以锁相环为核心的信号处理模块完成了信号解调;其次利用信号发生器来驱动扬声器，所发出的声音作用在玻璃板上产生声致振动作为振动源，实验探究了所述外差测量系统对于振动源驱动振幅、频率变化的响应;最后对该系统的应用进行了实验探究。实验结果表明，当频率在10 Hz～10 kHz频段内时，其测量误差小于0.15%，相对误差随着频率的增加而减小;解调信号幅值随着驱动电压的增大而增大，显示出了很好的响应度。对一小型旋转机械未故障、故障前后的振动进行了测量，记录了其波形以及频谱。测量结果表明，当旋转设备存在故障时其振动波形图发生明显变化;频谱分析结果显示，在175～250 Hz频段内，频谱幅值相对变小;在250～350 Hz频段内产生了新的频谱成分，从而验证了将该系统应用于小型旋转机械故障监测中的可行性。在后续的工作中将探索该系统更多的应用领域。

［1］ Dutton D，Givens M P，Hopkins R E.Some demonstration experiments in optics using a gas laser［J］.American Journal of Physics，1964，32(5):355－361.

［2］ Corcoran V J.Directional Characteristics in Optical Heterodyne Detection Processes［J］.Journal of Applied Physics，1965，36(6):1819.

［3］ Durst F，Melling A，Whitelaw J H.Principles and practice of laser－Doppler anemometry［M］.Beijing:Science Press，1992.(in Chinese)Durst F，Melling A，Whitelaw J H.激光多普勒测速技术的原理和实践［M］.北京:科学出版社，1992.

［4］ Protopipov V，Ustinov:N.Laser heterodyning［M］.Moscow:Izdatel Nauka，1985.

［5］ HE Yan，WANG Wenkui，XIA Wenbing，et al.Laser Doppler vibrometer for acousto－optic communication，Chinese Journal of Laser，2007，34(2):703－706.(in Chinese)贺岩，王文奎，夏文兵，等.激光多普勒振动计用于水下声光通信［J］.中国激光，2007，34(2):703－706.

［6］ HE Yan，SHANG Jianhua，LIU Dan，et al.Heterodyne laser doppler vibrometer for underwater acousto－optic communication［J］.Chinese Journal of Laser，2009，36(1):189－192.(in Chinese)贺岩，尚建华，刘丹，等.用于水下声光通信的外差式激光多普勒振动计［J］.中国激光，2009，36(1):189－192.

［7］ LI Xingfei，WANG Chi，XIANG Hongbiao，et al.Detection of weak ultrasonic signal using optical heterodyne interferometry［J］.Optics and Precision Engineering，2008，16(7):1158－1162.(in Chinese)李醒飞，王驰，向红标，等.光学外差干涉法检测微弱超声振动［J］.光学 精密工程，2008，16(7):1158－1162.

［8］ LIU Hongli，SHAO Lei，JIA Mingyan，et al.Study on laser Doppler technology in measurement of blast shock［J］.Journal of Vibration and Shock，2008，27(1):97－99.(in Chinese)刘宏利，邵磊，贾明雁，等.激光多普勒效应在爆炸冲击测量中的应用研究［J］.振动与冲击，2008，27(1):97－99.

［9］ Jianhua Shang，Yan He，Dan Liu，et al.Laser Doppler vibrometer for real－time speech－signal acquirement［J］.Chinese Optics Letters，2009，7(8):732－733.

［10］ HUO Lei，ZENG Xiaodong，AN Yuying，et al.Vibration measurement and analysis by means of laser Doppler heterodyne principle［J］.Laser Technology，2011，35(5):600－602.(in Chinese)霍雷，曾晓东，安毓英，等.利用激光多普勒外差原理对振动物体测量及分析［J］.激光技术，2011，35(5):600－602.

［11］ HUO Lei，ZENG Xiaodong，LIU Bing.Application of laser heterodyne interferometer in solid rocket motor vibration［J］.Journal of Solid Rocket Technology，2012，35(1):139－142.(in Chinese)霍雷，曾晓东，刘兵.激光外差干涉技术在固体发动机振动中的应用［J］.固体火箭技术，2012，35(1):139－142.

［12］ LI Feifei，WU Jin，ZHAO Zhilong，et al.Air coupled vibration detection of all－fiber laser doppler vibrometer［J］.High Power and Particle Beams，2012，24(11):2549－2554.(in Chinese)李斐斐，吴谨，赵志龙，等.全光纤激光多普勒测振仪空气耦合振动检测［J］.强激光与粒子束，2012，24(11):2549－2554.

［13］ LUO Yun，FENG Guoying，Liu Jian，et al.Vehicle identification technology of laser heterodyne spectrum analysis of vibration characteristics［J］.Chinese Journal of Laser，2014，41(11):1108001.(in Chinese)罗韵，冯国英，刘建，等.激光外差振动谱提取分析的车辆标识技术［J］.中国激光，2014，41(11):1108001.

［14］ Martinussen H，Aksnes A，Engan H E.Wide frequency range measurements of absolute phase and amplitude of vibrations in micro－and nanostructures by optical interfer-ometry［J］.Optics Express，2007，15(18):11370－11384.

［15］ Zhu Z，Li W，Wolberg G.Integrating LDV audio and IR video for remote multimodal surveillance［J］.Computer Vision and Pattern Recognition－Workshops，CVPR WorkshopsIEEE ComputerSocietyConference on，2005:10.

［16］ Kokkonen K，Kaivola M.Scanning heterodyne laser interferometer for phase－sensitive absolute－amplitude measurements of surface vibrations［J］.Applied Physics Letters，2008，92(6):063502.

［17］ Sommargren GE.Up/down frequency shifter for optical heterodyne interferometry［J］.JOSA，1975，65(8):960－961.

［18］ Wright O.Stabilized dual－wavelength fiber－optic interferometer for vibration measurement［J］.Optics letters，1991，16(2):56－58.

［19］ Park Y，Cho K.Heterodyne interferometer scheme using a double pass in an acousto－optic modulator［J］.Optics letters，2011，36(3):331－333.

［20］ XU Jieping.The Principle，Design and Application of A-cousto－optic Device［M］.Beijing:Science Press，1982.(in Chinese)徐介平.声光器件的原理、设计和应用［M］.北京:科学出版社，1982.

［21］ YU Kuanxin，DING Xiaohong，PANG Zhaoguang.Acousto－optic Principle and Devices［M］.Beijing:Science Press，2011.(in Chinese)俞宽新，丁晓红，庞兆广.声光原理与声光器件［M］.北京:科学出版社，2011.

［22］ LIANG Qiaochun，WANG Ying，CHEN Peifeng，et al.Investigation of spatial mismatch problems in laser heterodyne detection［J］.Laser ＆ Infrared，2011，41(1):43－50.(in Chinese)梁乔春，王英，陈培锋，等.激光外差探测中的空间失配问题研究［J］.激光与红外，2011，41(1):43－50.

［23］ LI Xiang，YANG Jinhua，JIANG Chenghao，et al.Study on collimation mismatch in laser heterodyne detection［J］.Laser＆ Infrared，2014，44(3):250－253.(in Chinese)李祥，杨进华，姜成昊，等.激光外差探测中准直失配问题的研究［J］.激光与红外，2014，44(3):250－253.