基于结构光三维重建系统的改进相位研究*
2021-11-29邓仕超陈艺海
邓仕超,陈艺海,黄 扬,梅 枫
(桂林电子科技大学广西制造系统与先进制造技术重点实验室,广西 桂林 541004)
0 引言
结构光三维测量因其非接触,速度快,精度高,广泛用于工业制造、质量检测、医学等领域,并成为学术界和工业界研究的重点[1-5]。在结构光测量系统中,条纹光栅解包裹是其中重要的一步,通过获取条纹的相位信息即可获取物体的三维信息。解包裹主要有空域和时域两种方法,空域解包裹在一定条件下只能重建简单的物体轮廓,对噪声敏感,容易出现累计误差[6-7]。在时域解包裹中,由于相移法计算简单,相位计算准确度高而被广泛应用[8]。在相移法中,在考虑时间效率和噪声抑制方面四步相移法用的最多,使用四步相移法计算得到包裹相位,相位处于[0,2π)之间,然后利用多频外差进行相位展开,进而获得全场绝对相位。
在实际工程应用过程中,外界环境存在的噪声、干扰,相机镜头畸变,投影仪非线性误差等因素会导致展开的相位产生跳变[9-11],使得三维重建结果表面不光滑不连续,测量精度变低。近年来,为了抑制解包裹条纹级数产生跳变,有一些学者对多频外差进行了改进,雷志辉等[12]对双频外差进行了改进,比较两个展开相位之间的误差来判断是否产生跳变,只适用于两频外差。陈玲等[13]对三频外差进了的改进,通过展开的相位与其相邻的相位进行比较进而判断是否发生相位跳变,这失去了每个点的独立性。陈松林等[14]对多频外差进行了改进,得到了很好的展开相位,但第三种光栅频率太低,对复杂形面分辨能力稍微不足。刘飞等[15]利用了全频信息,通过额外约束条件有效抑制了相位跳变。黄亚楠等[16]通过相邻10个像素点来抑制条纹级数跳变,如果存在阴影则相位矫正会受限,这些方法存在一些局限。
为了减小解包裹过程中的相位误差跳变,实现全场相位展开,在分析相位跳变产生原因的前提下,本文提出了误差范围约束,并利用了公式回带和所有展开的相位信息,正确展开了全场相位。本文算法实际解包裹结果相位准确,且三维重建结果表面光滑,细节清晰。
1 三频外差解包裹
由文献[14]可知,外差解包裹原理是指将多种不同频率的光栅图像叠加到一起进行解包裹的方法,最常用的是双频外差和三频外差。相对于双频外差解包裹,三频外差解包裹对细节的分辨能力更高[15]。本章先介绍三频外差原理,然后对其进行误差分析,最后在误差分析的基础上提出改进算法。
1.1 传统三频外差原理
根据文献[7],三频外差原理是首先通过相移法计算包裹相位,所谓相移法就是计算不同相移的正弦条纹的相位主值,计算出的主值相位包裹在[0,2π),然后通过三套不同频率的编码正弦条纹解出各自的包裹相位,通过第一套和第二套条纹外差、第二套和第三套条纹外差得到两套频率更低的条纹,再次通过这两套低频条纹外差形成全场只有一个周期的相位,称为第三次外差。最后通过第三次外差相位信息回解出三套条纹中的其中一套条纹的展开相位,图1是三频外差原理图,第一列是三套条纹的包裹相位,第二列是第一次和第二次外差频率更低的相位,第三列是第三次外差,全场只有一个周期。

图1 三频外差原理
首先利用四步相移法解出三套条纹的包裹相位φi(i=1,2,3)。
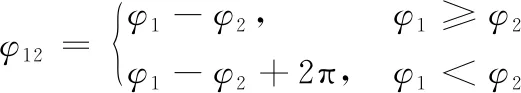
(1)

(2)

(3)
式(1)~式(3)中,φi(i=12,23,123)表示外差后的包裹相位。设3套光栅周期数分别为T1、T2、T3,对应的光栅节距为p1、p2和p3。
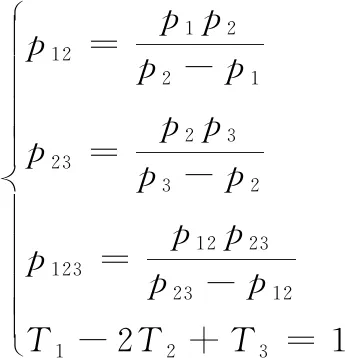
(4)
其中,条纹的周期数和节距需满足T1>T2>T3,p1 (5) (6) (7) 式(6)、式(7)表示第一套条纹的相位展开公式。展开相位用φi表示,i=1,2,3,12,23,123。 图2 φ123误差图 图3 n12-N12和Δn12误差图 为了能进行全场相位展开,提出如下改进的解包裹方法。理论上有式(8)成立: p1φ1=p2φ2=p3φ3=p12φ12=p23φ23=p123φ123 (8) 式(8)包含周期数为T1、T2、T3的展开相位和外差后三套条纹的展开相位。因为第三次外差得到的条纹周期数为1,所以φ123=φ123。根据图2及其分析,在没有级数跳变的地方,n12的小数部分(n12-N12)与Δn12之差存在一定误差范围(-a,a),在此范围内就没有产生条纹级数的跳变,此时a就是可接受的最大误差。ni-Ni-Δni的绝对误差为|Δni+a-floor(Δni+a)-Δni|=|1-a|,当a∈(0,0.5)发生相位跳变时,误差|1-a|∈(0.5,1)是大于0.5的,此时可以抑制误差;当a∈(0.5,1)发生相位跳变时,误差|1-a|∈(0,0.5)是小于0.5的,此时不能抑制误差,说明条纹小数部分最大能接受的误差为a=0.5。当ni-Ni-Δni小于-0.5时,说明条纹误差向下跳变,当ni-Ni-Δni大于0.5时,说明条纹误差向上跳变。 本文算法步骤如下: (1)首先利用式(6)计算n12和N12,用式(9)计算φi,i=12,23: (9) (2)因为n12和n23是经过有误差的φ123计算得到的。当N12或N23之中的一个发生跳变而另一个没有跳变时,求平均值可以减小这种误差: (10) 根据式(10)重新计算Δn123,回带第(1)步再次求出φ12、φ23。 (3) 根据式(11)和式(12)计算周期数为T1、T2、T3的条纹级数整数部分和展开相位,i=1,2,3: (11) (12) (4)在实际情况下式(8)是不成立的,利用所有展开的相位信息求平均值,进一步提高相位展开的准确性,利用式(13)计算最终相位,i=1,2,3: (13) 图4 传统算法e=π/26 图5 传统算法e=π/22 图6 本文算法e=π/26 图7 本文算法e=π/22 图8和图9是分别添加e=π/26随机误差,经传统算法和本文算法解得的n12-N12和Δn12的误差图,由图8可以看出,传统算法浅灰色部分(n12-N12)跳变误差较大,与深色部分Δn12存在较大偏差;可见本文算法修正后浅灰色部分的跳变相位抑制效果明显,两者偏差减小。 图8 传统算法n12-N12和Δn12 图9 本文算法n12-N12和Δn12 表1是本文算法和传统算法n12-N12和Δn12偏差对比表,这种引起最终相位跳变的误差被减小。由表可知,最大偏差绝对值能减少6 rad左右,标准偏差减少0.7 rad左右。 表1 n12-N12与Δn12的偏差 e=π/26 为实际验证本文算法的有效性和传统算法的局限性,搭建如图10所示的实验平台,使用德州仪器TI的投影仪DLP4500,分辨率为1140 pixel×912 pixel。使用陕西维视智造科技公司的相机,型号为MV-EM200C,分辨率为1600 pixel×1200 pixel。向物体投射周期数为140、134、129的光栅,周期数满足式(4)的条件,用三组实验分别对比传统算法和本文算法的解包裹和三维重建结果。 图10 实验平台 在本实验中,为了说明本文算法和传统算法的对比。使用投影仪向参考平面投影12幅光栅,相机同步拍照,使用本文算法和传统算法进行相位展开,结果如下:图11和图12是传统三频外差解包裹结果,图11中相位跳变的地方与图13相位展开图红圈相对应,图12和图14是本文算法解包裹结果,可以明显的看出本文算法可以很好的抑制相位误差,且展开的相位表面光滑,无任何相位跳变,正确展开了全场相位。 图11 传统算法φ1图12 本文算法φ1 图13 传统算法相位展开图 图14 本文算法相位展开图 进一步对比验证本文算法解包裹对平面度误差测量的精度,对3个不同标准金属块进行三维重建,3个标准金属块编号1,2,3,长宽高分别为40.4 mm,35.3 mm,15.2 mm;60.0 mm,35.0 mm,9 mm;34.9 mm,21.6 mm,18.0 mm,如图15所示,然后计算金属块上表面的3D平面拟合偏差,金属块1表面共有205 514个点,金属块2表面共有102 339个点,金属块3表面共有307 648个点。本文算法利用调制度分析去除不可靠区域后的相位展开图如图16所示。从表2可以看出,本文算法金属块表面的3D拟合偏差相对于传统算法更小,测量误差减少了大约28%。 图15 相机拍摄图 图16 相位展开图 表2 平面拟合的3D偏差 分别用传统算法和本文算法进行复杂形面三维重建形成头像对比本文算法和传统算法重建效果。图17为相机拍摄到的光栅投影后的人头模型。解包裹时使用调制度分析去除载物平面和阴影部分。传统算法重建结果如图18所示,本文算法重建结果如图19所示,可以看出传统算法三维重建结果表面部分信息缺失,而本文算法重建效果表面平滑,细节更清晰。 图17 相机拍摄图 图18 传统算法头像点云及其面部放大图 图19 本文算法头像点云及其面部放大图 表3是对应图18和图19总的点云数量,图18中面部放大图中的黑色竖条纹就是相位跳变误差引起的点云缺失,本文算法相对于传统算法点云数量增加了6477个,点云信息更加丰富,成像细节更突出。 表3 本文算法和传统算法重建点云数量 本文在分析传统三频外差解包裹产生相位跳变误差原因的基础上,提出了一种改进的算法,使用误差范围约束,并回带计算减小误差和利用所有展开的相位信息正确解出了全场相位。通过仿真实验给出了本文算法和传统算法对比,引起相位跳变的误差被矫正,说明本文算法对随机误差具有较强的抑制作用。三组真实实验结果表明,参考平面的解相结果相比传统算法,不存在相位跳变且相位表面光滑,不需额外方式进行相位矫正;三个标准金属块表面3D平面拟合偏差更小,实际应用程度进一步提高;三维重建结果表明,相比传统算法,本文算法头像点云平滑连续,细节清晰,而传统算法重建后表面部分信息缺失,三维重建系统的精度进一步提高。

1.2 误差分析
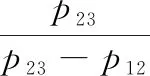
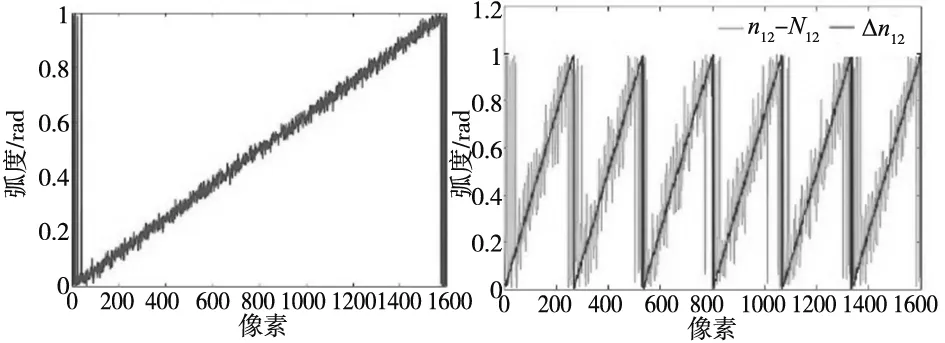
1.3 改进算法
2 仿真分析



3 实验分析

3.1 参考平面解包裹


3.2 测量标准金属块3D平面拟合偏差


3.3 人头模型三维重建



4 结论
