基于外差-分数阶傅里叶变换的线性调频连续波主动声呐处理
2018-04-27何明伟智达丁烽
何明伟 智达 丁烽
(第七一五研究所,杭州,310023)
随着现代潜艇技术的发展,潜艇的隐身性能显著提高,其辐射噪声级越来越小,现役声呐主要为脉冲式主动声呐,其发射脉冲脉宽较短,对目标的照射时间短,并且要经过一段较长时间才能侦听到回波信号,目标重访率低。这使得传统脉冲式主动声呐难以满足实战需求。为克服脉冲主动声呐的不足,近年来人们开始将注意力转移到连续波声呐模式下并取得了一定的研究进展。
声呐信号设计是主动声呐技术研究中的重要内容,决定了声呐系统的探测距离分辨率、速度分辨率、抗混响性能等[1]。连续波主动声呐利用连续发射的声信号进行目标探测,相比脉冲主动声呐具有连续跟踪、处理增益高、抗干扰性强等优势,是现代反潜战的热点和发展趋势。由于连续波主动声呐发射和接收工作同时进行,决定了连续波主动声呐一般工作在双基地或多基地模式,因此发射和接收之间的直达声干扰不可避免[2]。Stefan M Murphy等人在2015年提出了分子带处理方法[3],将较长的信号划分为若干子带,以得到更快的数据更新速率,但相应地降低了输出信噪比,处理时需要在二者之间折中考虑。本文中将回波信号与发射信号做外差,并利用分数阶傅里叶变换估计外差信号的调频斜率和中心频率,进而估计目标的位置和速度。
1 LFMCW信号模型
线性调频连续波(Linear Frequency Modulation Continuous Wave, LFMCW)的每个扫频周期内是线性调频(Linear Frequency Modulation, LFM)信号,表示为

式中T为发射信号周期,fl是发射信号起始频率,r为调频斜率。目标回波信号为发射信号的延时和多普勒频移:
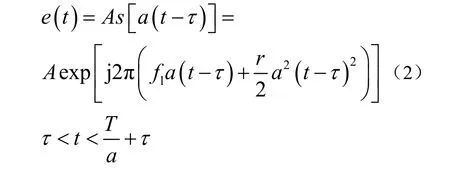
连续波主动声呐系统一般工作在收发分置模式下,在接收端收到的信号为直达声、目标回波和环境噪声的叠加: x(t) = s (t) + e (t) + n (t )。
外差方法可以被用来将信号频率方面的信息转换为时延或距离信息。将发射信号和回波信号分别降基带、低通滤波处理,得到基带信号 sb(t)和eb(t) ,则外差信号为

外差后得到的信号仍为线性调频信号,其中心频率fb和调频斜率rb分别为:

当目标静止时,外差信号为单频信号,此时对外差信号直接进行傅里叶变换即可得到目标的时延。当目标运动时,对运动目标回波信号的外差信号进行傅里叶变换会影响接收机处理增益。对一目标在静止状态和速度为3 m/s时的回波信号进行外差-傅里叶变换后的结果如图1所示。该信号的中心频率1 500 Hz、带宽500 Hz、脉宽90 s的LFMCW、距离为 7.5 km。运动目标不仅频谱扩展,幅度下降,并且距离估计值与静止时产生较大偏差。

图1 静止目标和运动目标的外差-傅里叶变换结果
2 外差-分数阶傅里叶变换处理算法
针对外差-傅里叶变换结构处理方式的局限性,本文提出了外差-分数阶傅里叶变换的处理算法,结构如图2所示。

图2 外差-分数阶傅里叶变换接收机结构
分数阶傅里叶变换是一种广义的傅里叶变换,它可以作为信号时频分析的工具,非常适合处理线性调频信号,函数 x (t)的p阶分数阶傅里叶变换定义为:
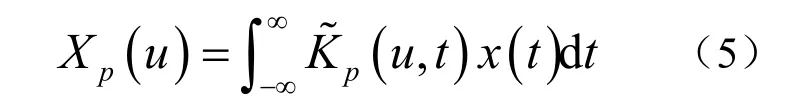
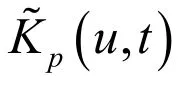

分数阶傅里叶变换存在多种快速计算方法,本文采用的是 Ozaktas提出的基于表达式分解的方法[5]。根据分数阶傅里叶变换的表达式,将FRFT分解为信号的卷积形式,从而利用 FFT计算FRFT。利用该算法的结果估计 LFM 参数前需要对原始信号进行量纲归一化[6]。对于 LFM 信号s(t),其进行分数阶傅里叶变换结果为Xα(u),通过对阶次和分数阶傅里叶域进行二维搜索,得到峰值坐标,即可估计LFM信号的参数。信号调频斜率rb和中心频率fb的估计问题可描述为:

根据式(7)得到外差信号的中心频率和调频斜率估计值,代入公式(4),计算出目标的时延τ和多普勒伸缩因子a,进而得到目标的距离和速度。
3 仿真结果分析
仿真验证上述提出的外差-分数阶傅里叶变换算法的可行性。LFMCW信号中心频率1 500 Hz,带宽500 Hz,周期 90 s,目标距离15 km,速度 20 m/s,信噪比-20 dB,接收直达声幅度为目标回波幅度的500倍,每段处理时间为30 s。将接收信号与发射信号进行外差,对外差信号进行分数阶傅里叶变换,扫描分数阶傅里叶变换阶次,得到二维FRFT结果,再取匹配阶次的 FRFT结果进行回波信号的参数估计,如图3所示。

图3 外差-FRFT 处理结果
通过扫描得到各段外差信号的匹配阶次,进而计算出各段信号的中心频率,得到各段外差信号的频率-时间显示 A式图和 B式图,仿真结果与理论值基本一致,如图4所示。从图4(c)中可以看出,外差方法将接收直达声和回波信号在频域上分开,通过滤波后可以将二者分开。
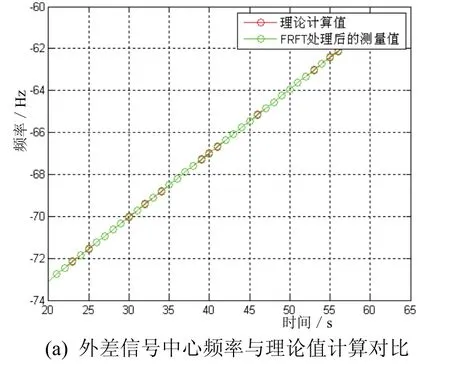
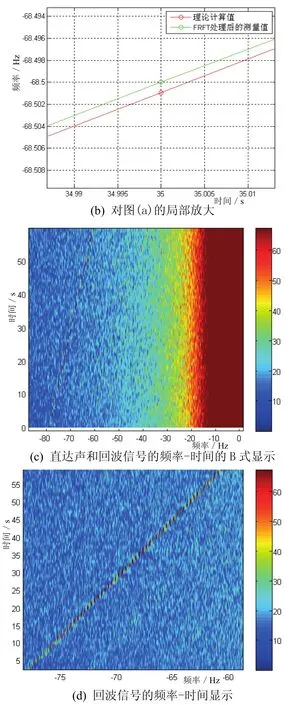
图4 各段外差信号的频率-时间的A式显示和B-式显示
利用各分段信号FRFT处理的频率结果,根据公式(4)计算出相应的时延τ和多普勒伸缩因子a,进而得到各时刻目标的距离和速度(如表1所示),取40个样本数据的平均值,得到目标距离为14 996 m,速度为20.017 2 m/s。仿真对比分析外差-分数阶傅里叶变换算法的检测性能:LFMCW连续波带宽500 Hz,脉宽90 s,每段处理时间为30 s,LFM脉冲脉宽1 s,信噪比-10 dB,结果如图5所示。LFMCW经外差-FRFT处理后的增益为10lg(500/90×30×30)=36.99 dB ,LFM 脉冲进行匹配滤波处理的增益为10lg(500×1)=26.9 dB,LFMCW经处理后比LFM处理得到的增益高10 dB。外差-FRFT算法能达到和匹配滤波相当的处理增益,说明外差-FRFT算法用于检测LFMCW信号是可行的。

表1 各时刻目标位置和速度

图5 LFMCW和LFM经处理后的输出信噪比对比
使用蒙特卡洛方法分析外差-分数阶傅里叶变换算法接收机对LFMCW的检测性能,通过对信噪比和检测概率的分析,得到接收机工作特性曲线,并将结果与脉冲信号做匹配滤波处理的工作特性曲线进行对比,如图6所示。试验过程中,LFMCW信号的中心频率1 500 Hz,带宽500 Hz,脉宽80 s,分段处理时间为10 s,处理带宽为62.5 Hz, LFM脉冲的中心频率1 500 Hz,带宽500 Hz,脉宽1 s,仿真的虚警概率为 10-4,信噪比范围均为-40 dB至-10 dB,信噪比间隔为-2 dB,从图6可以看出,当信噪比为-20 dB时,LFMCW连续波通过外差-分数阶傅里叶变换处理的检测概率已接近100%,而LFM脉冲进行匹配滤波处理后几乎检测不到信号,信噪比要提高到-10 dB时才能完全检测到信号。仿真说明外差-分数阶傅里叶变换用于LFMCW连续波检测是可行的,也说明连续波检测目标比脉冲具有更大的优势。
4 结论
连续波主动声呐中发射和接收之间不可避免地存在直达声干扰,如何解决直达声干扰是连续波主动声呐研究中的关键问题。本文通过将发射信号与接收信号进行基带外差处理,能有效抑制直达声干扰问题,以及基于分数阶傅里叶变换检测和估计线性调频信号的原理,提出的外差-分数阶傅里叶变换算法,能够实现对目标回波信号的检测和目标参数估计。不同于Stefan M Murphy等人提出的分子带处理方法,本文对接收信号进行分段相干处理,连续地获取目标参数;但对发射信号的处理局限于单分量的情况,在多个线性调频信号周期发射时,对接收信号进行分数阶傅里叶变换会使得能量聚集效果变差,需要在本文算法的基础上进一步研究讨论。
参考文献:
[1] 吴迪, 周泽民, 曾新吾. M-COSTAS复合编码连续主动声呐信号研究[J]. 信号处理, 2016, 32(10):1187-1193.
[2] 庞博, 吴一飞, 刘本奇. 连续波声呐中的调频信号设计方法及性能分析[J]. 声学技术, 2017(4):327-334.
[3] MURPHY S M, HINES P C. Sub-band processing of continuous active sonar signals in shallow water[C]. Oceans.IEEE, 2015:1-4.
[4] 郭斌. 分数阶Fourier变换的基本原理与应用[D]. 电子科技大学, 2006.
[5] OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9):2141-2150.
[6] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4):360-364.
