缺陷参量对光子晶体缺陷模奇偶性的调制

苏安，蒙息君，蒋丹，白书琼

(河池学院 物理与机电工程学院，广西 宜州 546300)

0 引言

光子晶体［1－2］是一种具有光子带隙的人工光学材料，它是由不同折射率介质周期性排列形成的［3－14］。大量的研究成果已经表明，当入射到光子晶体中的电磁波频率处于带隙结构的导带频率范围时，被允许传播，当频率处于禁带范围内时则被禁止传播。当在周期性排列的介质之间插入恰当的缺陷时，光子晶体特定位置特别是缺陷位置处的自发辐射得到增强，这种增强的自发辐射能提高电磁波通过光子晶体的能力，并在透射能带谱中形成透射率很高的缺陷模(透射峰)［11－13］。光子晶体对光的这种禁止和选择性通过机制，为人为控制和利用光提供了理论支撑，特别是对光通信领域提出了新的传输方法，从而有人预测不久的将来，光子晶体最有可能替代电子作为信息传输的新载体［3－14］。

所以，怎样在光子晶体周期性排列的介质之间置入缺陷，就能根据人的意识控制光的传输行为，即实现特定的透射功能，以满足设计和应用需要，是研究者和设计者们面临也是必须解决的问题，也是大家都关注的焦点。当前，关于含缺陷光子晶体的研究很多，研究成果报道文献也不少，但单独研究缺陷自身结构参量变化对光子晶体缺陷模的影响，尤其是缺陷自身参量变化对宏观表现上的缺陷模奇偶性的影响，还未见报道。基于这种思考，本文在构造一维光子晶体模型(AB)m(ACxB)k(AB)m的基础上，研究缺陷数目k、缺陷周期数x和缺陷厚度dC变化时缺陷模奇偶性的变化，找出三者对缺陷模奇偶性的调制规律，为光子晶体的理论研究、新型光学器件的设计制备等提供参考。

1 研究模型和方法

研究模型为(AB)m(ACxB)k(AB)m，其中A、B是周期性排列的光子晶体基元介质，C是插入A、B介质周期性排列中的缺陷，m是光子晶体基元介质A、B的排列周期数，k是插入缺陷C的(AB)单元数，亦即缺陷数，x是缺陷层C自身的排列周期数，研究计算时，m、k和x均可取正整数。A、B和C介质层对应的折射率和厚度分别为:nA=2.6，nB=1.45，nC=4.1，dA=740 nm，dB=1 329nm，dC=469.3 nm。显然，结构模型中 C层介质的光学厚度nCdC等于A层介质的光学厚度nAdA。

研究采用数值计算和仿真模拟结合的方式进行，主要对象为一维光子晶体的透射能带谱，由于计算量不大，因此计算方法采用比较直观且相对较成熟的研究方法——传输矩阵法［3－14］。计算模拟步骤是通过科学计算软件MATLAB编程，对各含缺陷光子晶体模型的传输矩阵进行编程计算，绘制出不同缺陷参量情况下光子晶体的透射能带谱，并观察、分析这些参量对透射谱中缺陷模的影响规律。鉴于传输矩阵法在很多文献中已经有比较详细地介绍，且应用已经很普遍，因此在此不再赘述，详细可见文献［14］。

2 计算结果与分析

2.1 缺陷数目对缺陷模奇偶性的调制

在光子晶体(AB)m(ACxB)k(AB)m研究模型中，(AB)是光子晶体基元介质周期性排列的基本单元，如果没有缺陷C，研究模型就是标准的准周期性结构模型(AB)m，这种结构光子晶体的透射能带谱是普通的带隙结构，即透射能带谱由较宽的禁带和相对较窄的通带构成。当某个周期排列单元(AB)中插入缺陷C，准周期结构即被打破，则在光子晶体禁带中出现窄带的缺陷模(透射峰)。从(ACxB)k排列结构可以看到，当缺陷自身周期数x=1时，那么k其实就是缺陷数目，例如，当k=1时，光子晶体模型结构可表示成(AB)m(ACB)(AB)m，此时相当于(AB)周期性结构中插入了一块缺陷C，即含一块缺陷，k=2、3、4….时模型所含的缺陷数目可依次类推。为找出缺陷数目对光子晶体缺陷模奇偶性的影响规律，可进一步地固定光子晶体基元介质排列周期数m=5，缺陷自身周期数x=1，k=1～8，然后分别以k为奇数和偶数时对应的(AB)5(ACB)k(AB)5透射能带谱作图，如图1所示。

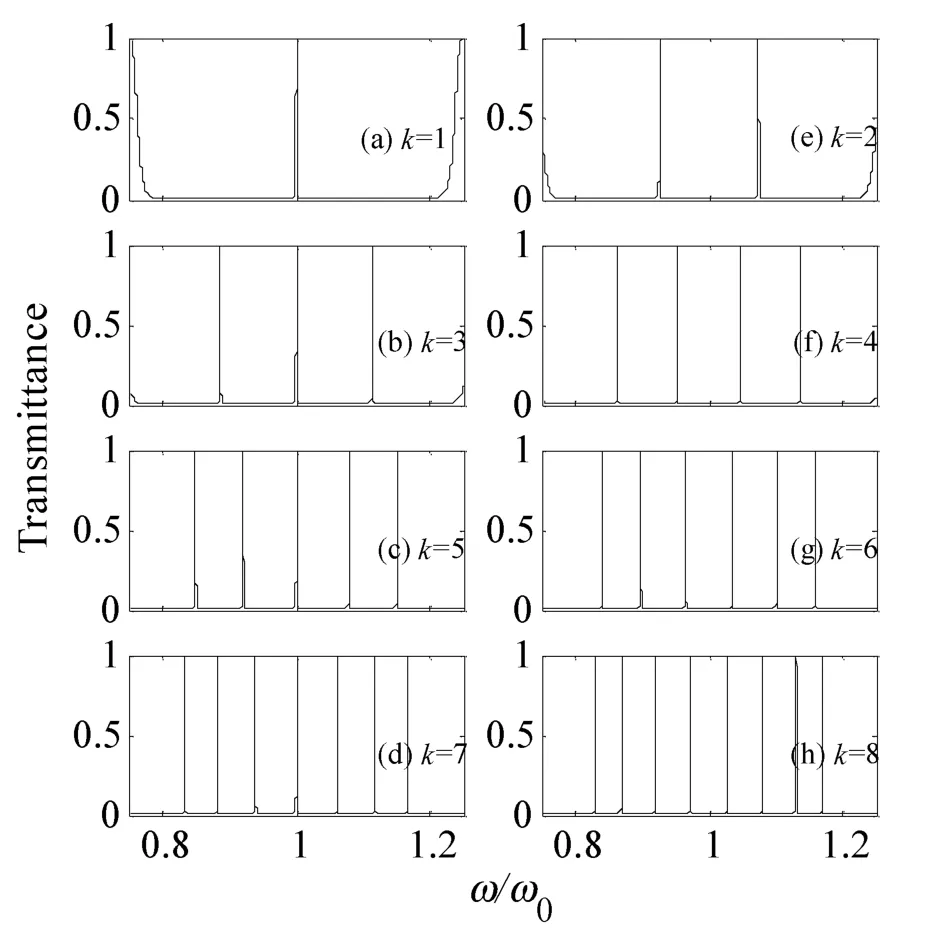
图1 缺陷数目对光子晶体(AB)5(ACB)k(AB)5缺陷模奇偶性的调制

从图1可见，当缺陷数目k为奇数(k=1、3、5、7)时，随着k的增大，禁带中的缺陷模数目增加，而且缺陷模条数与缺陷数目一一对应，即也为奇数条，如图1(a～d)所示。当缺陷数目k为偶数(k=2、4、6、8)时，随着k的增大，禁带中的缺陷模数目也增加，而且缺陷模条数与缺陷数目一一对应，即为偶数条，如图1(e～h)所示。另外，从图1(a～h)还看到，随着k的增大，光子晶体的禁带变宽，禁带中缺陷模条数增加的同时它们之间的距离越来越小，且缺陷模的带宽越来越窄，即缺陷模越来越精细且相互之间等间距排列得越来越密。

因此，缺陷数目不仅可以决定缺陷模数目的奇偶性，而且两者奇偶性是对应的。同时缺陷数目还可以调节缺陷模的带宽以及它们之间的距离。缺陷数目对缺陷模的这些调制特性、规律对奇偶性通道光学滤波器件的研究和设计等具有一定的参考价值。

2.2 缺陷周期对缺陷模奇偶性的调制

当基元介质排列周期中插入缺陷后，缺陷不仅可以跟着其所在介质单元排列周期进行变化，而且还可以以自身的排列周期进行变化，自身排列周期也分奇偶数，自身排列周期变化对缺陷模的奇偶性又会产生什么样的影响呢，这不仅是我们想知道的，并且目前也还未见报道。基于这种考虑，仍然取m=5，缺陷数目则取k=1，缺陷自身周期数取x=1～8，然后分别以x为奇数和偶数时对应的(AB)5(ACxB)k(AB)5透射能带谱作图，如图2所示。

从图2可见，当缺陷自身周期x为奇数(x=1、3、5、7)时，随着x的增大，禁带中的缺陷模数目为奇数，但缺陷模数目与缺陷数目不等值。当x=1、3时，禁带中保持1条缺陷模，当x=5时，禁带两侧开始新增两条不完整的缺陷模，当x=7时，新增的两条缺陷模变得精细完整，即禁带中缺陷模增加到3条，即缺陷模总条数仍然为奇数，如图2(a～d)所示。而当缺陷自身周期数x为偶数(x=2、4、6、8)时，随着x的增大，禁带中的缺陷模数目为偶数，而且缺陷模数目与缺陷数目也不等值，x=2、4、6、8时，禁带中一直保持2条缺陷模不变，如图2(e～h)所示。进一步计算发现，当x=10时，禁带两侧开始新增两条缺陷模，当x=12时，新增的两条缺陷模变得精细完整，此时禁带中缺陷模增加到4条，即缺陷模总条数仍然为偶数。继续以整数增大x计算发现，禁带中的缺陷模条数变化与以上变化规律相似，即缺陷模条数的奇偶性与缺陷自身周期数x的奇偶性有关，但不形成等值对应关系。

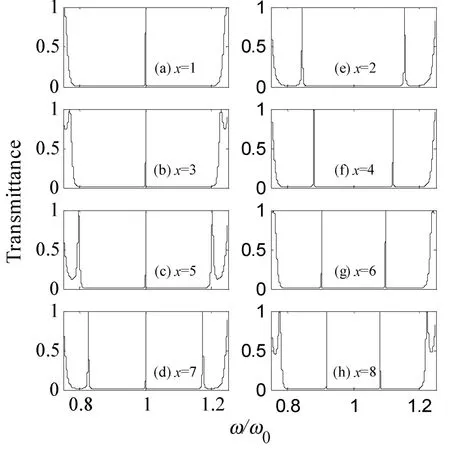
图2 缺陷周期数对光子晶体(AB)5(ACxB)(AB)5缺陷模奇偶性的调制

从图2中还看到，当缺陷自身周期数x为偶数时，禁带中的缺陷模随着x的增大逐渐向禁带中心靠拢，而当x为奇数时，禁带中心的缺陷模则一直保持在1.00ω/ω0频率位置不变。

可见，利用周期性排列介质单元中的缺陷自身周期数x，同样可以对光子晶体缺陷模的奇偶性进行调制，且周期数x在偶数情况下还可以对缺陷模所处的频率位置进行调制，这对光学滤波器件和光学开关的研究与设计等具有借鉴意义。

2.3 缺陷厚度对缺陷模奇偶性的调制

周期性排列组成光子晶体介质薄膜的尺寸可以用物理厚度和光学厚度来衡量。物理厚度亦简称为厚度，是薄膜的几何尺寸之一，光学厚度则是物理厚度与介质折射率之积［8，12］，在设计制造上，物理厚度是必须考虑的因素之一。从光学厚度的定义可知，当介质的物理厚度改变时，其光学厚度也自然随之改变，同时其周期性排列形成的光子晶体结构亦随之改变，最终也一定会对透射谱特性产生影响。因此，介质物理厚度对光子晶体缺陷模奇偶性的影响机制，也是关心和须知晓的问题之一。

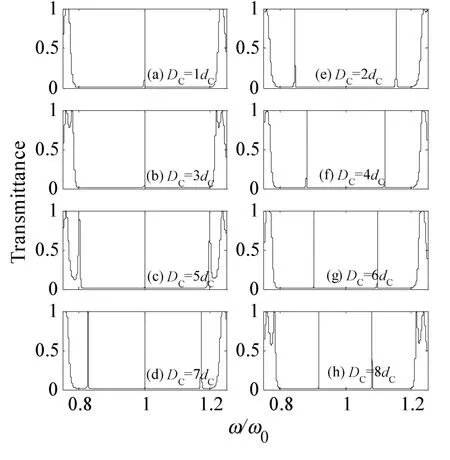
图3 缺陷厚度对光子晶体(AB)5(ACB)(AB)5缺陷模奇偶性的调制

仍然保持基元介质(AB)的排列周期m=5，缺陷数目则取k=1，缺陷自身周期数x=1，以DC表示缺陷层厚度dC的倍增值，并使DC=1dC～8dC整数倍递增，分别绘制出缺陷厚度dC的奇数倍和偶数倍递增时光子晶体(AB)5(ACB)(AB)5透射能带谱，如图3所示。

从图3可见，随着缺陷厚度dC的奇数倍和偶数倍递增，禁带中出现的缺陷模条数也具有奇偶性，而且奇偶性的规律与缺陷自身周期数x影响缺陷模的奇偶性规律类似，如图3(a～h)所示。鉴于相似性及文章篇幅，在此不再做重复分析。

2.4 缺陷折射率对缺陷模奇偶性的调制

薄膜介质的折射率也是光子晶体重要的结构参数之一，它的变化涉及到薄膜的光学厚度改变，并导致光子晶体整个结构的改变，最终影响透射谱或缺陷模的特性。基于这个思路，仍然取m=5，k=1，x=1，以nC表示缺陷层C 的折射率，并使nC=4.1、4.2、4.3、…、4.8 逐渐递增，分别绘制出缺陷折射nC为奇数和偶数时光子晶体(AB)5(ACB)(AB)5透射能带谱，如图4所示。

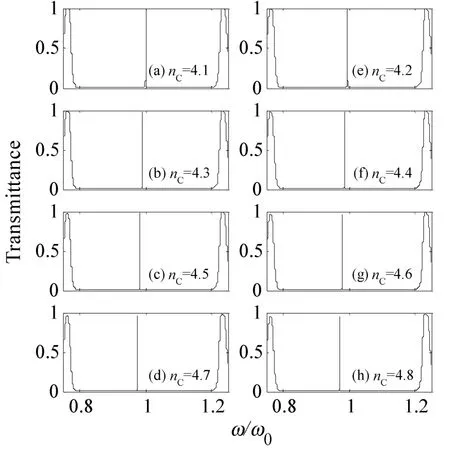
图4 缺陷折射率对光子晶体(AB)5(ACB)(AB)5缺陷模奇偶性的调制

从图4可见，无论缺陷C的折射率nC按奇数还是按偶数增大，禁带中的缺陷模均保持1条不变，即缺陷折射率nC对缺陷模的条数及其奇偶性不产生影响。但随着nC增大，禁带中的单缺陷模均缓慢地向低频方向移动，而且nC增大到一定数值后，缺陷模的透射率会慢慢下降。如，当nC=4.1时，单缺陷模处于禁带中的1.000 ω/ω0频率位置处，透射率T=100%，当nC=4.5时，单缺陷模移到禁带中的0.983 3 ω/ω0频率位置处，透射率T=96.85%，当nC=4.7时，单缺陷模则移到禁带中的0.975 7 ω/ω0频率位置处，透射率T=95.47%，如图4(a、c、d)所示;当nC=4.2时，单缺陷模处于禁带中的0.996 0 ω/ω0频率位置处，透射率T=98.84%，当nC=4.6时，单缺陷模移到禁带中的0.979 5 ω/ω0频率位置处，透射率T=96.24%，当nC=4.8时，单缺陷模则移到禁带中的0.972 0 ω/ω0频率位置处，透射率T=94.55%，如图 4(e、g、h)所示。

虽然，缺陷折射率nC对缺陷模的奇偶性不产生影响，但却可对缺陷模所处的频率位置进行调制。这种特性对光子晶体设计单通道光学滤波器件，以及光学开关等有着积极的参考意义。

3 结论

通过传输矩阵法理论，研究缺陷参量对光子晶体缺陷模奇偶性的影响规律，结论如下:

(1)插入光子晶体中的缺陷数目奇偶性直接影响缺陷模数目的奇偶性，而且缺陷模数目与缺陷数目相等。

(2)缺陷自身的周期数、缺陷厚度的奇偶性也影响缺陷模的奇偶性，但缺陷模数目与缺陷自身的周期数、缺陷厚度不存在一一对应关系。

(3)缺陷折射率奇偶性对缺陷模的数目和奇偶性不产生影响，但却影响缺陷模所处的频率位置和透射率，而且奇偶情况下影响规律相同。

利用缺陷参量对缺陷模的奇偶性调制机制和原理，可设计制备可调性奇、偶数通道光学滤波器件，以及光开关等。

［1］Yablonovitch E.Inhibited spontaneous emission in solid － state physics and electronics［J］.Phys.Rev.Lett.，1987，58(20):2 059 －2 061.

［2］John S.Strong localization of photons in certain disordered dielectric superlattices［J］.Phys.Rev.Lett.，1987，58(23):2 486 － 2 489.

［3］苏安，高英俊.双重势垒一维光子晶体量子阱的光传输特性研究［J］.物理学报，2012，61(23):234208.

［4］苏安，蒙成举，高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制［J］.中国激光，2014，41(3):0306001.

［5］苏安，蒙成举，高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器［J］.中国激光，2013，40(10):1006001.

［6］苏安，高英俊，蒙成举.双重势垒一维光子晶体量子阱内部局域电场分布［J］.光子学报，2014，43(2):0216002.

［7］苏安，李忠海，莫传文，等.光子晶体滤波器的滤波品质调制因素研究［J］.河池学院学报，2014，34(5):78－82.

［8］潘继环，苏安，蒙成举.介质光学厚度对光子晶体透射谱特性的调制［J］.激光与红外，2014，44(5):559－562.

［9］潘继环，苏安，蒙成举，等.垒层周期不对称度对光量子阱透射谱的影响［J］.激光与光电子学进展，2014，51(1):012701.

［10］苏安，蒙成举，潘继环，等.周期不对称度对光子晶体透射谱特性的影响研究［J］.量子光学学报，2014，14(2):154－158.

［11］苏安，蒙成举，高英俊，等.两端对称缺陷对对称结构光子晶体透射谱的影响［J］.激光与红外，2014，44(11):1 253－1 257.

［12］苏安，陆华，黄星寿.缺陷光学厚度对对称结构一维光子晶体透射谱的影响［J］.河池学院学报，2011，31(2):17－21.

［13］苏安，李现基.实现多种通道滤波功能的一维光子晶体缺陷模［J］.激光与红外，2010，40(5):532－536.

［14］王辉，李永平.用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50(11):2 172－2 178.