光子晶体的基本研究方法对比与实例分析

2015-03-16唐秀福

河池学院学报 2015年2期

唐秀福

(河池学院物理与机电工程学院，广西宜州 546300)

0 引言

光子晶体［1－2］作为一种新型的光学材料，在激光、通讯、医学等各领域都具有广泛的应用，对光子晶体的理论研究已成为近代光学研究的热门话题［3－17］。光子晶体是一种根据实际应用需要生产配制的人造光学材料，通过具有不同的介电常数的材料薄膜介质周期性排列起来，构成能够对光波进行调制的特殊功能，根据薄膜介质材料周期排列的维数不同，目前的光子晶体主要分为1维光子晶体、2维光子晶体和3维光子晶体。自1987年John S和Yablonovitch E分别独立提出光子晶体的概念之后，由于光子相比电子的诸多优越性，在光电领域激发了人们极大的研究热情，在接下来的几十年里对光子晶体的理论研究发展过程中，研究者不仅构建了大量的光子晶体模型，而且创造和使用了很多种有效的研究方法，并取得了大量研究成果［3－17］。目前常见的光子晶体理论研究方法主要有:平面波展开法、传输矩阵法、时域有限差分法、多重散射法、N阶法、转移矩阵法等，这些方法在对光子晶体特性的研究上都具有各自的优点和特点，同时针对不同的研究目标和对象，他们的适用范围也不一样［13－17］。因此，面对众多的研究方法，光子晶体的研究者特别是初学者难免无从选择最有效的方法去解决问题。基于这种思路，本文主要就光子晶体的主要研究方法的特点进行对比分析，得出各自的优缺点，确定各种研究办法的适用范围，并就其中最普遍使用的传输矩阵法进行实例计算模拟和分析，此举可为光子晶体的研究者和学习者提供参考。

1 光子晶体的基本研究方法及对比

1.1 光子晶体理论研究的基本方法

平面波展开法是利用Maxwell方程在傅利叶展开的平面波函数中将能带计算化为代数本征值问题求解，该方法是光子晶体理论研究中应用的最早也是最广的方法之一。平面波法是光子晶体早期研究中总结出来的一套最基本的理论计算方法，它对各种理想结构的晶体能带结构计算能够得出很好的结果。矩阵法是在光学薄膜计算中常用的一种计算方法，它也是利用Maxwell方程将光子晶体带隙问题转化为本征值的求解。传输矩阵法是在矩阵法的基础上发展得来的，它可以利用传输矩阵来描述晶体的周期性结构，是目前使用较为普遍的一种光子晶体理论计算方法。时域有限差分法是由Yee K S在1966年创建的，该方法的主要思想是对微分形式的Maxwell方程进行差分求解，将Maxwell方程组在坐标系中展开成标量场分量的方程组，然后在划分好的Yee氏网格空间中迭代计算出光子晶体中在任意时刻场的分布情况。多重散射法主要应用于二维有限光子晶体的问题求解中，该方法将光子晶体作为散射体放置于开放系统中，通过电磁波与散射体的相互作用，研究目标的散射、吸收和透入等相关特性。

此外，晶体研究的理论方法还有N阶法、转移矩阵法、格林函数法等。每种研究方法都各具特点，鉴于文章的篇幅及研究方法使用的普通性等，下面重点对平面波展开法、传输矩阵法、时域有限差分法和多重散射法进行对比分析。

1.2 常用光子晶体理论研究方法的对比

平面波展开法与其他研究方法相比，计算量较大是该方法的最大约束。由于该种计算方法的计算量与所用平面波的波数的立方几乎成正比关系，因此，对于一些复杂结构的晶体，特别是带缺陷的非理想晶体结构，计算量将非常大，甚至是无法计算。此外，对于介电常数不是恒定的晶体时，是无法得出确定的本征值方程，进而无法求解问题。故平面波展开法仅适用于计算结构简单的理想晶体能带。

传输矩阵法与其他计算方法相比，其优势在于计算量比较小。因为该方法中的传输矩阵仅与晶体层面上的格点数的平方成正比，且矩阵比较小、阵元少，因此计算量大为降低。此外，就计算过程而言，应用矩阵法运算得到的结果精确度要比矢量法高。利用传输矩阵法可有效计算1维、2维、3维介质或金属光子晶体的能带结构、透射系数、反射系数和内部电场分布等，对平面波法无法解决的电常数随频率变化的金属系统也特别适用，即便是对存在色散或者缺陷的晶体结构，该方法仍然可以有效计算。

时域有限差分法和传输矩阵法一样，不但可以有效计算光子晶体介质结构的能带机构，也可以计算金属结构的光子晶体能带关系。同时，该方法是处理光子晶体Anderson局域态、光子晶体波导本征模、光子晶体表面模特性的系列问题的有效方法。虽然时域有限差分法在计算晶体能带结构和传输特性上具有较大的优势，但由于该方法计算误差较大，不适用于对精确度要求高的问题，无法有效解决诸如特殊形状的原胞或复杂结构的光子晶体结构问题。

多重散射法对研究由规则散射体构成的晶体非常适用，对球体或者柱体散射体构成的晶体，利用该方法计算尤为优越，主要体现在收敛速度快，计算精确度高。此外，多重散射法在解决一些特殊问题上效果非常好，如在计算不同相的各种物质组成的晶体，尤其对高和低填充率两种极端情况时具有很好的收敛速度，缺点是计算复杂，使用比较困难。

在众多光子晶体理论研究基本方法中，传输矩阵法具有理论简单、计算量小、使用范围广、易于编程实现等诸多优点，因此在光子晶体理论研究中被广泛采用，特别是对光子晶体初学者而言，传输矩阵法是较为理想的研究方法之一。因此，下面将以传输矩阵法为例详细介绍其计算研究的基本原理，并构建一维光子晶体模型进行计算和分析，以加深读者的理解和掌握。

2 传输矩阵法原理及实例分析

2.1 传输矩阵法原理

由不同介电常数的两种薄膜介质A、B周期性排列形成光子晶体结构ABABABAB…，也可以表示成(AB)m，m就是基元介质(AB)单元的重复排列周期数。当光从左侧入射到光子晶体中时，在每一层介质中的行为均可用一个分矩阵来描述，这个分矩阵的推导如下［13－14，17］。

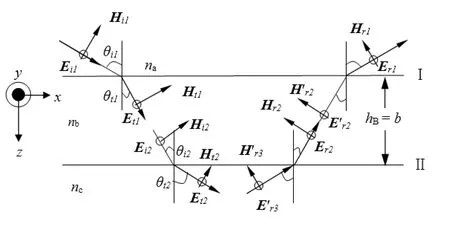
图1 光在任一单层薄膜介质中的传播行为

如图1所示，假设介质内不存在自由电荷和传导电流时，则在每层介质边界处，电磁场的分量都是连续的。界面Ⅰ处的入射、反射和透射电场和磁场分别记为Ei、Er、Et和 Hi、Hr、Ht，光以 θi1角入射到界面Ⅰ，θi2为界面Ⅱ的入射角。则利用界面Ⅰ和界面Ⅱ电场、磁场之间的关系，以及界面Ⅰ和界面Ⅱ上的透射场 Et1(x，y，z=0)、Ei2(x，y，z=b)，可得:

MB就是光在B层介质中传播行为的传输矩阵，在其他层介质(包括缺陷层介质)中同样适用。于是对于光在光子晶体结构中传播时，光的总行为为各分矩阵之积，表示为:

利用矩阵元A、B、C和D就可以计算光入射到光子晶体后的如下参量:

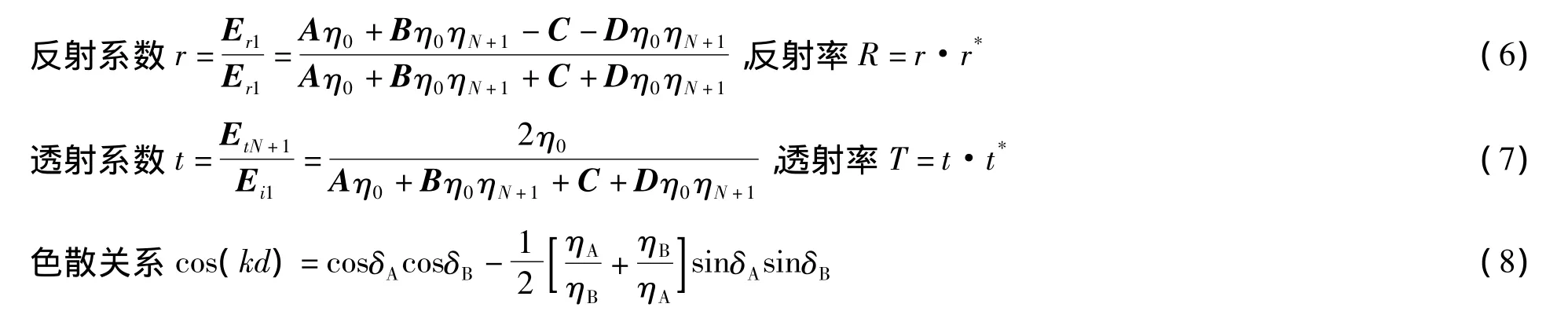
2.2 传输矩阵法计算模拟实例

研究的对象为A、B两种介质的色散曲线及其周期排列形成准周期光子晶体模型结构(AB)m，以及镜像对称模型结构(AB)m(BA)m。A、B介质计算的参数(折射率和厚度)分别为:nA=1.38，dA=281 nm，nB=2.35，dB=165 nm，m是基元介质单元(AB)的排列周期数，在计算中一般取正整数。

首先根据式(7)和(8)，由科学计算软件MATLAB编程，绘制出由A、B组成的晶体的色散曲线和由10个(AB)单元周期性排列形成的准周期结构光子晶体(AB)10的能带结构，如图2所示。图中坐标用归一化频率单位ω/ω0。

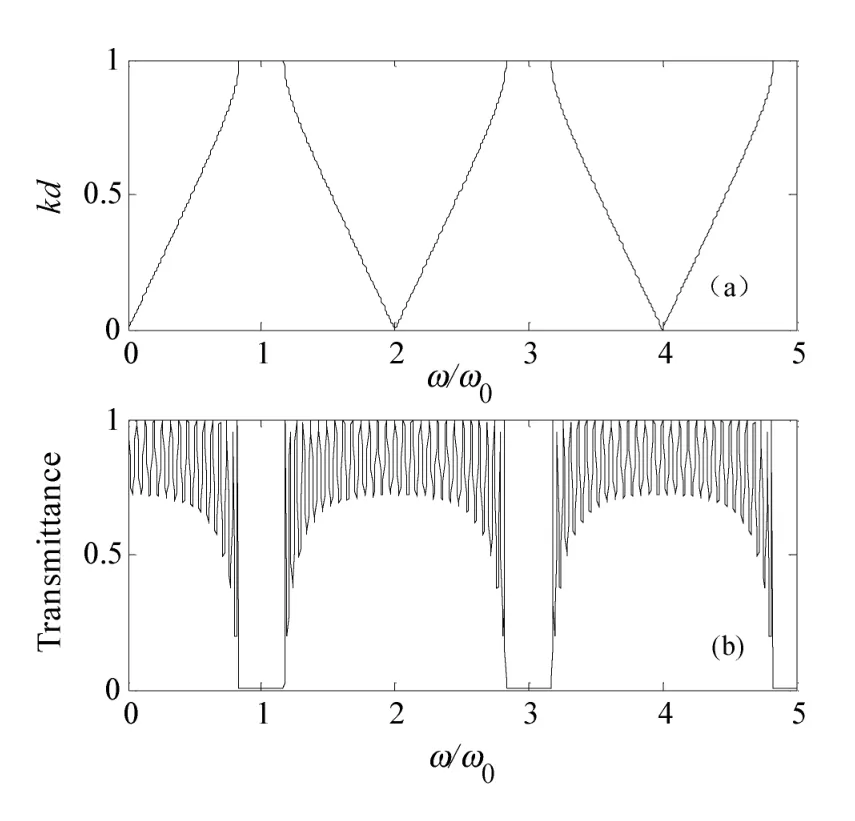
图2 色散关系和能带结构图

从图2可见，A、B介质组成的晶体的色散曲线存在着明显的带隙结构，其中在奇数倍频率处周围出现禁带，在偶数倍频率处周围则出现导带，如图3(a)。光子晶体(AB)10的能带结构与A、B晶体的色散曲线相对应，也是在奇数倍频率处周围出现禁带，而在偶数倍频率处周围则出现通带，如图3(b)所示。即光子晶体对入射到其中的光具有很明显的选择性通过功能［13－14］。模拟结果可见，用传输矩阵法很容易把入射到光子晶体中的光的行为描述出来，而且描述结果形象直观。

上述模拟的是光子晶体无缺陷的情形，当合理地在光子晶体的介质之间插入缺陷时，可以增强光子晶体特别是缺陷位置处的自发辐射，增强的自发辐射将使光很容易通过光子晶体，并在禁带中形成精细的缺陷模(透射峰)。对于含缺陷光子晶体的缺陷模，用传输矩阵计算模拟同样也很方便。介质A、B的参数不变，以A、B排列成镜像对称结构光子晶体(AB)8(BA)8模型，利用传输矩阵法计算模拟出其透射能带谱，如图3所示。从光子晶体结构(AB)7ABBA(BA)7模型可知，光子晶体镜像对称结构中心由于缺少一层 A 介质而形成空位缺陷［3，10，12］，即模型中带边框的，当光入射到光子晶体中时，此处的自发辐射会增强，于是在禁带中会出现透射峰即缺陷模。鉴于透射能带谱是周期性重复结构及文章的篇幅，图3仅绘制出0.5～1.5ω/ω0频率范围的能带谱。从图3可见，禁带中心出现了一条透射率为100%的缺陷模。所以传输矩阵法很方便且准确地描述了光在光子晶体缺陷中的传播行为，这对研究者和学习者均有积极的意义。

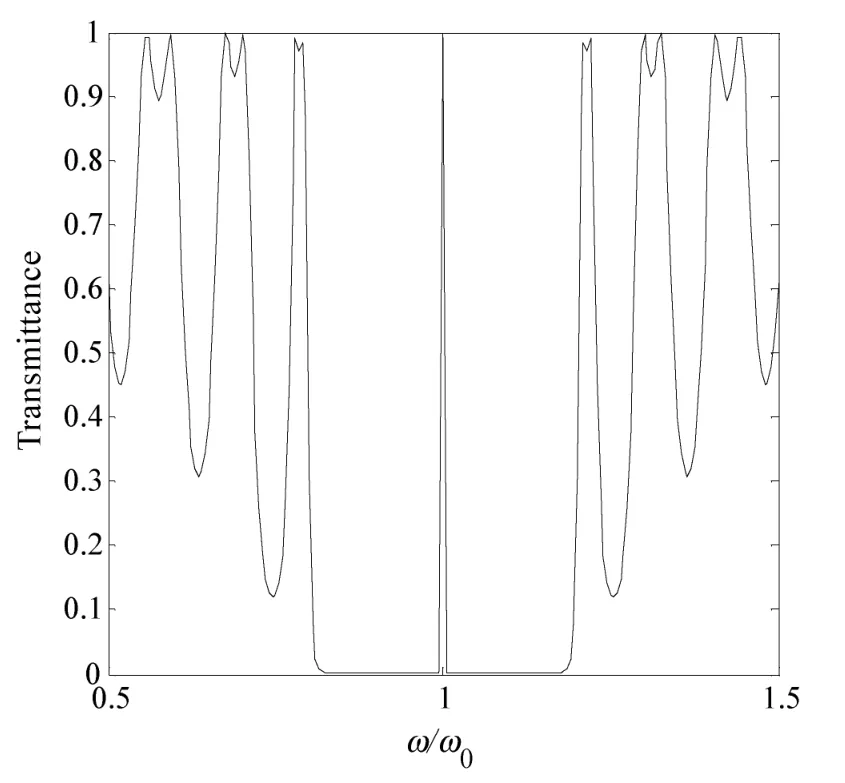
图3 光子晶体(AB)8(BA)8的透射能带谱

3 结论

通过对光子晶体常见研究方法的计算原理、运算工作量及运算精度等各方面的对比分析，得出如下结论:平面波展开法在计算理想光子晶体能带结构方面具有较大优势;传输矩阵法计算量小，能有效地用于晶体的能带结构、透射系数、反射系数和内部电场的计算，同时还可应用于金属晶体的计算与特性分析;有限时域差分法是计算光子晶体能带、带隙结构和传输特性的有效方法，同时也适用于解决Anderson局域态、波导本征模的特性等问题;多重散射法能很好的解决某些特殊问题，尤其对高和低填充率两种极端情况，更是具有很好的收敛速度。不同的研究方法具有各自的优越性的同时，也存在自己的局限性，在学习和研究光子晶体的实际计算问题时，应该根据不同的具体问题选用恰当的方法，才能有效地解决问题。

［1］Yablonovitch E.Inhibited spontaneous emission in solid － state physics and electronics［J］.Phys.Rev.Lett.，1987，58(20):2 059 － 2 061.

［2］John S.Strong localization of photons in certain disordered dielectric superlattices［J］.Phys.Rev.Lett.，1987，58(23):2 486 － 2 489.

［3］苏安，高英俊.双重势垒一维光子晶体量子阱的光传输特性研究［J］.物理学报，2012，61(23):234208.

［4］苏安，蒙成举，高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制［J］.中国激光，2014，41(3):0306001.

［5］苏安，蒙成举，高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器［J］.中国激光，2013，40(10):1006001.

［6］苏安，高英俊，蒙成举.双重势垒一维光子晶体量子阱内部局域电场分布［J］.光子学报，2014，43(2):0216002.

［7］苏安，李忠海，莫传文，等.光子晶体滤波器的滤波品质调制因素研究［J］.河池学院学报，2014，34(5):78－82.

［8］潘继环，苏安，蒙成举，等.垒层周期不对称度对光量子阱透射谱的影响［J］.激光与光电子学进展，2014，51(1):012701.

［9］潘继环，苏安，蒙成举.介质光学厚度对光子晶体透射谱特性的调制［J］.激光与红外，2014，44(5):559－562.

［10］苏安，陆华，黄星寿.缺陷光学厚度对对称结构一维光子晶体透射谱的影响［J］.河池学院学报，2011，31(2):17－21.

［11］苏安，蒙成举，高英俊，等.两端对称缺陷对对称结构光子晶体透射谱的影响［J］.激光与红外，2014，44(11):1 253－1 257.

［12］苏安，高英俊.含复介电常数一维光子晶体的滤波特性［J］.中国激光，2009，36(6):1 535－1 538.