2024-T3铝合金拉伸及剪切断裂行为

姜 薇，李亚智，苏 杰，束一秀

(西北工业大学 航空学院，西安 710072)



2024-T3铝合金拉伸及剪切断裂行为

姜 薇，李亚智，苏 杰，束一秀

(西北工业大学 航空学院，西安 710072)

2024铝合金材料在拉伸和扭转载荷作用下表现出截然不同的失效机理。结合试验和数值方法，研究了应力状态对2024-T3铝合金韧性断裂行为的影响规律。首先，对圆棒和薄壁圆筒试验件分别进行了拉伸和扭转试验，从断面形貌以及断裂应变与应力状态间关系两个方面，考察了应力状态对2024-T3铝合金断裂机理的影响规律。然后，基于Gurson理论在商业有限元软件ABAQUS中开发了同时适用于拉伸和剪切断裂模式的细观损伤本构，对2024-T3铝合金的弹塑性响应和裂纹扩展路径进行了数值分析。与试验结果对比研究表明，本文发展的细观损伤本构能够较好预测延性金属材料在多种应力状态下的损伤破坏过程。

延性断裂；拉伸失效；剪切失效；细观损伤模型；Gurson理论

0 引言

延性金属材料的断裂过程强烈地依赖于应力状态，在不同应力三轴度作用下，呈现出截然不同的断裂机理[1-3]。高应力三轴度时，微孔洞扩张引起材料软化，随后发生由孔洞之间韧带颈缩主导的破坏；低应力三轴度时，微孔洞的体积并不发生明显变化，但形状发生明显改变(旋转、扭曲)，最终导致孔洞间韧带剪切主导的破坏。Bao和Wierzbicki[4-5]针对不同几何形状的试验件，试验研究了断裂应变与应力三轴度之间的关系，考察了2024铝合金材料在不同应力状态中的破坏行为。Fan等[6]和Liu等[7]基于连续损伤力学方法，考察了静水应力和罗德角参数对延性材料破坏的影响，提出了适用于多种应力状态的宏观损伤模型。

延性材料的断裂过程通常可看作是材料内部微孔洞的形核、扩展及相互贯通的积累。细观损伤力学将微孔洞的演化规律嵌入到弹塑性本构关系中，并结合材料的连续属性与宏观可测量的断裂阻力相关联，最显著的优点是采用单个单元就可描述材料在微孔洞影响下的响应历程，从而显著降低细观到宏观尺度上对材料表征的差异性。经典Gurson理论[8]能够描述拉伸静水应力作用下，微孔洞的成长过程及其对材料承载力的影响。Tvergaard和Needleman对Gurson模型进行了一系列补充和修正[9-11]，考虑了孔洞间的相互作用以及材料的应变强化效应，补充了对孔洞贯通过程的描述，提出了适合的孔洞萌生准则。尽管如此，Gurson-Tvergaard-Needleman(GTN)模型仍然不能用于模拟剪切载荷主导的失效过程。在此基础上，Nahshon 和 Hutchinson[12]将依赖于罗德角参数的修正项引入到GTN模型的孔洞体积变化方程中，从而考虑了剪切变形作用，能够很好地模拟低应力三轴度作用下的延性材料破坏过程。基于剪切损伤机理研究，Xue[13]将孔洞体积分数与剪切损伤项组合起来定义成新的损伤参数，用在GTN屈服函数中。

本文研究了2024-T3铝合金材料在拉伸和剪切载荷作用下的破坏机理。基于Nahshon和Hutchinson对GTN模型的修正，开发了同时适用于拉伸和剪切破坏的细观损伤本构，并采用商业有限元软件ABAQUS的用户自定义子程序功能进行编程实现，考察了2024-T3铝合金在拉伸和扭转载荷作用下的塑性响应和裂纹扩展路径。

1 细观损伤模型

1.1 三轴应力状态

应力空间中的任意三轴应力状态OP可由主应力分量(σ1,σ2,σ3)确定，也可由一组表征应力不变量的柱坐标来表示，如图1所示。 其中，OA经过原点并且与3个主应力轴夹角相等，称作静水轴，经过P点并且垂直于OA的平面，称作偏平面。在该柱坐标系中，OP由(OA,AP,θ)确定，其中，OA为静水分量，AP为偏分量，θ称为罗德角，是σ1轴在偏平面上的投影逆时针旋转到AP时扫过的角度。通过数学变换，可得3个柱坐标值与应力张量的第一不变量(I1)、应力偏张量的第二不变量(J2)及第三不变量(J3)之间的关系：

(1)

其中

I1=-3p=3σm=σ1+σ2+σ3

(σ2-σ3)2+(σ3-σ1)2]

J3=det(s)=(σ1-σm)(σ2-σm)(σ3-σm)=s1s2s3

式中σ1、σ2、σ3为主应力分量；s=σ+pI为应力偏张量，I是二阶单位张量；s1、s2、s3是应力偏张量的3个主值；σm是平均应力；p是静水应力；q是等效应力。

因此，应力三轴度参数T和罗德角参数ξ可完全确定出空间内的任意应力状态，被广泛用于延性材料断裂研究。

(2)

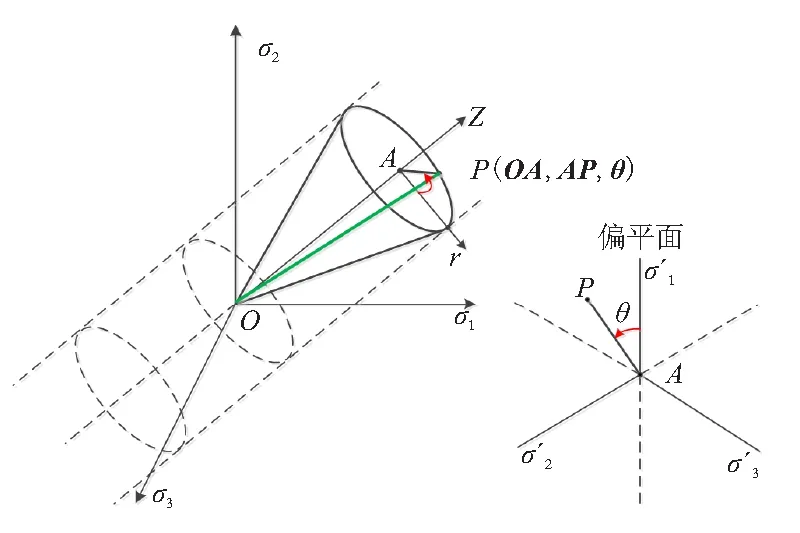
图1 主应力空间中的应力状态

1.2 GTN损伤本构

Gurson理论假设材料由基体(不含孔洞的密实材料)和微孔洞两部分组成，屈服面由等效应力q，静水应力p以及损伤变量(孔洞体积分数，f)共同决定。考虑了孔洞贯通过程的GTN屈服函数具有以下形式[9]。

(3)

(4)

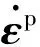
f*函数用来考虑孔洞的贯通作用：

(5)

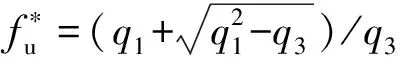
载荷作用下，孔洞体积分数的改变主要源于已有孔洞的扩张以及新孔洞的萌生。其中，孔洞的长大量仅与塑性体积改变有关，即

(6)

新孔洞萌生的主要形式是基体粒子在界面处的断裂或脱粘，可采用塑性应变控制的孔洞萌生模型来描述，即

(7)

(8)

式中fN为孔洞体积分数中形核部分的极限值；εN为孔洞萌生时的平均等效塑形性应变；sN为该正态分布的标准差。

1.3 修正的细观损伤本构

剪切载荷并不会直接导致材料内部的孔洞体积增大。但孔洞的形状和方向都会发生改变，从而导致材料出现软化，并且不断累积引起材料损伤失效。GTN模型假定孔洞的长大仅由塑性体积改变决定。因此，只在拉伸静水应力的作用下，才会出现损伤破坏。纯剪切状态下静水应力为零，若采用GTN模型，则孔洞不会长大和贯通，材料也不会失效。Nahshon和Hutchinson[12]在GTN模型基础上，定义了一个新的应力函数来区分应力状态。考虑主应力空间中的任意三轴应力状态，并假设σ1>σ2>σ3，考虑到应力偏张量的第三不变量J3与应力分量的关系：

J3=(σ1-σm)(σ2-σm)(σ3-σm)

(9)

(10)

该应力函数取值范围是[0，1]，且在轴对称应力状态时ω=0，纯剪应力状态叠加静水应力状态时ω=1。

基于此，为考虑剪切作用下孔洞的形状和方向都会发生改变带来的损伤，引入了一个等效的孔洞体积分数改变量[12,14]。

(11)

纯剪切应力状态时有

(12)

(13)

可见，此时剪切损伤率(等效孔洞体积分数变化率)与剪应变呈线性关系，而等效孔洞体积分数是剪应变的指数函数。剪切损伤系数kω用来标定纯剪应力状态时的损伤量。因此，可由剪切或扭转试验结果确定。

考虑剪切作用的孔洞体积分数变化方程具有以下形式：

(14)

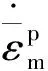
2 2024-T3铝合金拉伸及扭转试验

2.1 拉伸及扭转试验

本文研究的2024-T3铝合金材料常数为杨氏模量E=71 GPa，泊松比υ=0.33，初始屈服强度σ0=345.6 MPa。为考虑不同应力状态和断裂模式，分别进行了圆棒拉伸试验和薄壁圆筒扭转试验。其中，拉伸试验件包含光滑圆棒(Smooth round bar, SRB)及3种缺口圆棒(Notched round bar, NRB：R12,R6,R3)，这些试验件在拉伸载荷的作用下，随缺口半径不同，具有不同的应力三轴度水平，而薄壁圆筒试验件提供了近似纯剪的应力状态。图2给出了各试验件的几何形状、尺寸细节及载荷形式。表1给出了加载过程中各试验件在损伤起始处的近似应力三轴度水平T和罗德参数ξ。

拉伸和扭转试验均在东京理科大学机械工程学部的双轴液压伺服MTS测试机上进行。拉伸试验的加载速率为0.002 mm/s，轴向位移的监测范围是试验件中部50 mm的部分。扭转试验时，夹持头间距为36 mm，试验机直接记录两夹持端转过的相对角度，加载速率为0.02 rad/s。每种试验件重复试验4次，以保证试验数据的有效性。

2.2 试验结果

2024-T3铝合金的断裂试验结果显示，拉伸和扭转载荷作用下，材料表现出了2种完全不同的断裂机理。图3(a) 为拉伸试验得到的NRB-R6试验件断裂面照片，呈现出典型的“杯锥状”形式：中心是“纤维区和放射区”，由大量显著长大的平均直径在10 μm数量级的孔洞构成，宏观上呈现出粗糙的韧涡型断口，图3(b)给出了NRB-R6试验件断裂面中心位置的电镜扫描图像；四周的“剪切唇”区域断面则相对平整，与试验件轴线呈45°角度。“纤维区和放射区”具有较高应力三轴度，微孔洞在拉伸静水应力作用下不断地形核、长大、贯通，材料内部的孔洞体积明显增大，属于孔洞间韧带颈缩控制的断裂机理控制；“剪切唇”区域应力三轴度水平较低，孔洞长大不明显，属于微孔洞韧带剪切控制的断裂机理。试验件在外载荷作用下，裂纹首先在对称截面中心处萌生，扩展至自由面过程中，由孔洞间韧带颈缩控制的断裂机理过渡为微孔洞韧带剪切控制的断裂机理，从而形成了“杯锥状”断口。

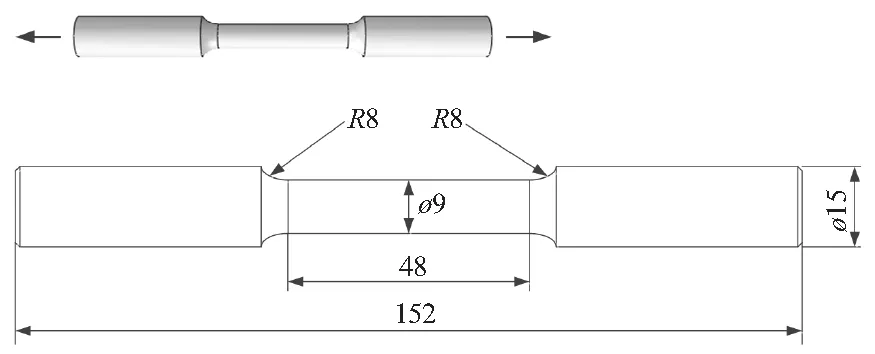
(a) 光滑圆棒

(b) 缺口圆棒

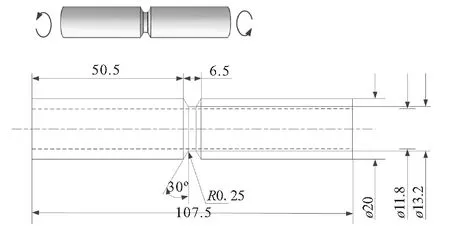
(c) 扭转试验件

参数SRBR12R6R3TorsionT1/30．480．620．830ξ11110

图4是薄壁圆筒试验件的扭转断裂面，裂纹在试验件的薄壁段向厚壁段过渡的转角处萌生，沿径向向内扩展，最终穿透截面。薄壁圆筒扭转试验中，受低应力三轴度(T=0)影响，微孔洞不能直接长大，但会在剪切应变作用下不断地变形和扭曲，从而积累损伤，属于微孔洞韧带剪切控制的断裂机理。剪切断裂模式中，孔洞体积一般不会发生明显变化。因此，呈现出平整的断裂面。

(a) NRB-R6试验件断裂面形状

(b) NRB-R6试验件断面中心处电镜扫描图像

图4 扭转试验件断裂面

实际工程结构中，韧性断裂过程通常都是2种破坏机理共同作用的结果，且材料的韧性伴随着自孔洞间韧带颈缩控制的断裂机理向韧带剪切控制的断裂机理的过渡而减弱。宏观上表现为拉伸载荷作用下，断裂应变常大于扭转载荷下断裂应变。图5所示为2024-T3铝合金在不同应力状态下，裂纹起始处的临界破坏应变随应力三轴度的变化曲线。

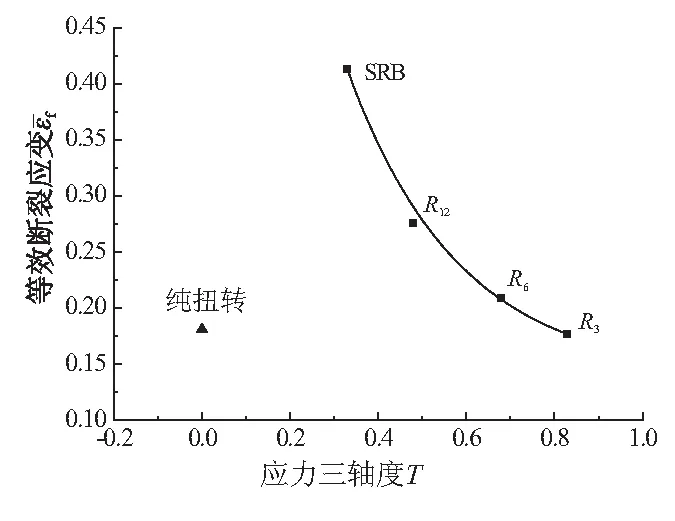
图5 等效断裂应变随应力三轴度演变曲线

可看出，单轴拉伸情况下，破坏应变随应力三轴度水平的增长而单调减小，近似服从指数关系；相对于拉伸，扭转载荷下材料的破坏应变更低。扭转试验中的断裂应变演化不遵循拉伸试验中所得到的断裂应变随应力三轴度单调递减的规律，进一步说明了2024-T3铝合金材料在拉伸和剪切载荷作用下存在不同的破坏机理，也意味着需要引入新的参数(如罗德单数)来准确描述断裂应变与应力状态之间的关系。

3 2024铝合金断裂过程有限元分析

3.1 塑性响应

ABAQUS/Standard和ABAQUS/Explicit的材料库中，均提供了基于Gurson理论的多孔金属塑性材料模型，但仅在Explicit求解模块中，考虑了孔洞的贯通过程，允许用户定义材料的失效过程[15]。由于该材料模型不能用于模拟剪切主导的破坏模式，本文在考虑孔洞贯通的GTN本构的基础上，结合 Nahshon和Hutchinson针对剪切破坏模式所进行的修改(下文称作GTN-H模型)，分别在Standard和Explicit中借助于用户材料子程序(UMAT和VUMAT)，开发了同时适用于拉伸和剪切破坏分析的细观损伤本构，用于分析2024-T3铝合金的断裂行为。

为考虑材料的应变强化作用，需要输入真实应力-应变曲线。本文使用Ramberg-Osgood形式拟合光滑圆棒单轴拉伸试验中所得到的真实应力-应变曲线。表2给出了采用GTN-H模型模拟2024-T3铝合金材料的破坏过程时的细观损伤参数。对轴对称拉伸试验件和薄壁扭转试验件进行有限元分析时，分别使用4节点缩减积分轴对称单元(CAX4R)和8节点缩减积分体单元(C3D8R)，建立1/2模型并施加对称边界条件。采用缩减积分单元配合UMAT进行有限元分析时，需要对单元的沙漏刚度进行控制。

表2 细观损伤模型参数

图6和图7分别给出了光滑圆棒和缺口圆棒拉伸试验件的弹塑性响应曲线的试验和模拟结果。对比研究可看出：(1)对光滑圆棒试验件和缺口圆棒试验件，UMAT和VUMAT都给出了非常一致的计算结果，该材料本构模型能够很好预测延性材料的拉伸及剪切断裂行为；(2)应力三轴度强烈地影响着材料的拉伸断裂特性。圆棒拉伸试验中，缺口半径R越小(对于光滑圆棒，R=∞)，试验件对称截面上的应力三轴度T越高，所承受载荷水平也越高，最终的断裂位移越小。由于所有圆棒试验件最小截面积相同，且轴向位移的监测范围相同，可得到如下结论：随着应力三轴度T的增加，材料的拉伸强度不断提高，断裂应变不断降低。

图8为薄壁扭转试验件的弹塑性响应曲线。

图6 光滑圆棒弹塑性响应模拟结果

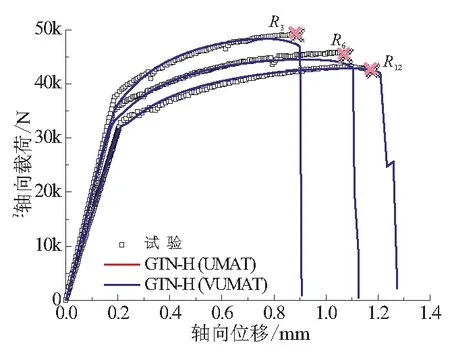
图7 缺口圆棒弹塑性响应模拟结果

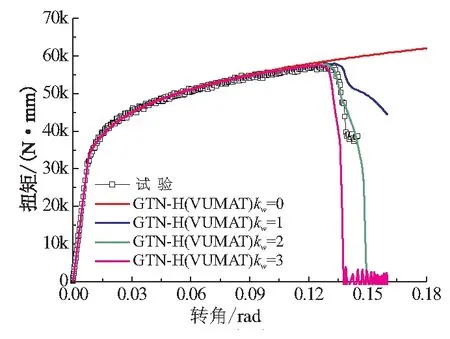
图8 扭转试验件弹塑性响应模拟结果

剪切损伤参数kω=0时，孔洞体积分数变化方程(式(12))中考虑剪切作用的修正项不发挥作用，即GTN-H损伤本构退化为传统的GTN本构。尽管GTN本构模型可较好地模拟变形起始阶段的材料扭矩-转角响应过程，但随着载荷的持续作用，无法有效地预测材料在剪切载荷作用下的软化现象，也不能模拟出材料失效过程。图8中还比较了kω取值分别为1、2、3时的计算结果。结果表明，kω=2时，GTN-H损伤本构能够准确模拟出材料在剪切载荷作用下的损伤演化过程。

3.2 裂纹扩展路径

理论上，UMAT虽然更适合分析准静态过程，但ABAQUS/Standard中不能进行单元删除，无法模拟出裂纹扩展路径；加之，隐式有限元方法中，需提供切线模量来建立切线刚度矩阵(雅可比矩阵)，以便采用牛顿法求解全局方程，这使得载荷下降阶段的计算常出现收敛性数值问题[15]。鉴于VUMAT也能够给出可靠的全局弹塑性响应计算结果，本文采用基于显式有限元方法的VUMAT模拟裂纹的扩展路径。计算中，当某个单元完全失去承载能力即由损伤本构计算得到的应力为0时，删除该单元，并认为裂纹在此萌生，而逐个删除单元的路径即为裂纹的扩展路径。与计算全局弹塑性响应不同，模拟裂纹扩展路径时常常需要借助于更精细的有限元网格，以便准确捕捉裂纹的起始和扩展位置。图9(a)为NRB-R6试验件对称截面附近的有限元网格。由于在颈缩过程中，变形主要集中在对称截面附近，网格会沿轴线被拉长，为了使单元在接近破坏时有近似于1的长高比，在初始剖分时，采用图9所示的30 μm×20 μm的单元。图9(b)为薄壁扭转试验件的有限元模型及裂纹可能萌生区域附近的有限元网格，在预期的裂纹扩展路径附近的三维实体单元的周向边长为100 μm，径向和轴向边长为50 μm。最后，为了减少计算消耗，对所有试验件，只在靠近损伤破坏区域的范围内使用GTN-H损伤单元，其余部分使用普通的Mises单元(见图9)。

GTN损伤本构仅能用于模拟纯I型的裂纹扩展，无法处理剪切主导的破坏模式。因此，如果采用GTN模型模拟圆棒拉伸试验，裂纹将会沿最小截面直线扩展，无法模拟出拉伸试验所观测到的“杯锥状”的破坏面。此外，在GTN模型框架下，由于单元仅在剪切载荷作用下不会出现损伤失效，即没有裂纹会在剪切载荷下萌生、扩展，因而GTN模型也不能用来模拟薄壁圆筒的扭转试验。为此，本文采用修正的GTN损伤本

构模型(即GTN-H)对拉伸和剪切载荷下的断裂行为进行分析。图10～图12 分别给出了采用GTN-H损伤模型模拟的SRB试验件、NRB-R6试验件及薄壁圆筒试验件的裂纹扩展过程中的Mises云图。拉伸试验中，对称截面中心处具有最高的应力三轴度水平，微孔洞在拉伸静水应力作用下迅速地形核、长大，首先发生卸载，裂纹在此萌生，并沿径向直线扩展，接近外表面时，由于应力状态的改变，裂纹发生偏折形成剪切唇，较好地模拟出了“杯锥状”的断裂面，如图10和图11所示。

(a) NRB-R6试验件对称截面附近

(b) 裂纹可能萌生区域附近

薄壁圆筒扭转试验中，薄壁段的应力三轴度和罗德参数值都接近0，受接近纯剪的应力状态作用。裂纹在剪切变形最大的薄壁段向厚壁段过渡的转角处萌生，随后在剪应变的作用下沿径向向内扩展，最终穿透截面，如图12所示。可看出，本文的损伤本构可用于模拟多种应力状态下不同类型的裂纹扩展过程。

(a) 裂纹起始 (b) 裂纹扩展 (c) 最终破坏

(a) 裂纹起始 (b) 裂纹扩展 (c) 最终破坏

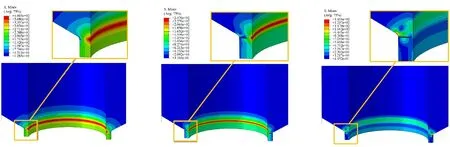
(a) 裂纹起始 (b) 裂纹扩展 (c) 最终破坏

4 结论

(1)应力三轴度显著影响2024-T3铝合金的韧性，随着应力三轴度的增加，材料的拉伸强度不断提高，断裂应变不断降低。

(2)非负应力三轴度(零静水应力或拉伸静水应力)作用下，2024-T3铝合金表现出了2种依赖于应力状态的断裂机理。拉伸断裂过程属于孔洞韧带颈缩过程控制的断裂机理，孔洞体积明显增大，断裂面呈现出粗糙的韧涡型断口。剪切断裂过程属于微孔洞韧带剪切作用控制的断裂机理，孔洞体积一般不会发生明显变化，呈现出平整的断裂面，相对于拉伸破坏，具有较小的破坏应变。

(3)计及剪切作用的细观损伤本构模型不仅能够预测2024-T3铝合金材料在多种应力状态下的弹塑性响应，也可用于模拟多种应力状态下不同类型的裂纹扩展过程。

[1] Faleskog J, Barsoum I. Tension-torsion fracture experiments-Part I: Experiments and a procedure to evaluate the equivalent plastic strain[J]. International Journal of Solids and Structures, 2013, 50: 4241-4257.

[2] Xue Z Y, Faleskog J, Hutchinson J W. Tension-torsion fracture experiments-Part II: Simulations with the extended Gurson model and a ductile criterion bases on plastic strain[J]. International Journal of Solids and Structures, 2013, 50(25): 4258-4269.

[3] Barsoum I, Faleskog J. Rupture mechanisms in combined tension shear-experiments[J]. International Journal of Solids and Structures, 2007, 44: 1768-1786.

[4] Bao Y, Wierzbicki T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Science 2004, 46:81-98.

[5] Bao Y, Wierzbicki T. On the cut-off value of negative triaxiality for fracture[J]. Engineering Fracture Mechanics, 2005, 72: 1049-1069.

[6] Fan X L, Sun Q, Liu Y J. A modified ductile fracture model incorporating synergistic effects of pressure and Lode angle[J]. International Journal of Applied Mechanics, 2012, 4 (2):1250022 (16 pages).

[7] Liu Y J, Sun Q, Fan X L, et al. A stress-invariant based multi-parameters ductile progressive fracture model[J]. Materials Science & Engineering A, 2013, 576(1):337-345.

[8] Gurson A L. Continuum theory of ductile rupture by void nucleation and growth: part I yield criteria and flow rules for porous ductile media[J]. Journal of Engineering Materials and Technology, 1977, 99: 2-15.

[9] Tvergaard V. On localization in ductile materials containing spherical voids[J]. International Journal of Fracture, 1982, 18(4): 237-252.

[10] Tvergaard V, Needleman A. Analysis of the cup-cone fracture in a round tensile bar[J]. Acta Metallurgica, 1984, 32(1): 157-169.

[11] Chu C C, Needleman A. Void nucleation effects in biaxial stretched sheets[J]. Journal of Engineering Materials and Technology, 1980, 102: 249-256.

[12] Nahshon K, Hutchinson J W. Modification of the Gurson model for shear failure[J]. European Journal of Mechanics A/Solids, 2008, 27:1-17.

[13] Xue L. Constitutive modeling of void shearing effect in ductile fracture of porous material[J]. Engineering Fracture Mechanics, 2008, 75: 3343-3366.

[14] Xue Z, Pontin M G, Zok F W, et al. Calibration procedure for a computational model of ductile fracture[J]. Engineering Fracture Mechanics, 2010,77: 492-509.

[15] 庄茁. 连续体和结构的非线性有限元[M]. 北京：清华大学出版时, 2011.

(编辑：薛永利)

Tensile and shear failure mechanisms of 2024-T3 aluminum alloy

JIANG Wei, LI Ya-zhi, SU Jie, SHU Yi-xiu

(School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China)

Under tensile and shear loading conditions, 2024 aluminum alloy exhibits two types of distinctive ductile rupture mechanisms. The growth and internal necking of voids governs the rupture mechanism in tension dominated loading mode, while the internal shearing in the ligaments between voids dominants for shear conditions. To investigate the influence of stress states on the material ductility of 2024-T3 aluminum alloy, tensile experiments of a smooth round bar and three notched round bars with different notch root radii as well as a pure torsion experiment were performed. Based on the modification of Gurson model by Nahshon and Hutchinson, a void-based meso-damage constitutive relationship which can deal with both tensile and shear problems was developed and implemented in commercial software ABAQUS. The tensile and shear fracture behaviors of 2024-T3 aluminum alloy including the load-displacement response and crack propagation path were analyzed using the proposed approach and compared with experimental data. It is shown that the proposed approach can be used to predict the failure of ductile materials under complex loading conditions.

ductile fracture；tensile failure；shear failure；meso-damage model；Gurson theory

2014-06-23；

2014-07-19。

国家自然科学基金(11272259)。

姜薇(1987—)，女，博士生，研究方向为金属韧性断裂研究。E-mail:jiangwei0525@mail.nwpu.edu.cn

V252

A

1006-2793(2015)03-0426-07

10.7673/j.issn.1006-2793.2015.03.025