基于三维CFD的RBCC发动机建模方法
2015-03-13潘宏亮何国强王亚军
潘 浩,潘宏亮,秦 飞,何国强,王亚军
(西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072)
基于三维CFD的RBCC发动机建模方法
潘 浩,潘宏亮,秦 飞,何国强,王亚军
(西北工业大学 燃烧、热结构与内流场重点实验室,西安 710072)
RBCC发动机可多模态工作,能适应宽广的飞行包线,因而其火箭尾流剪切作用变化强烈、流道截面变化大,喷油规律复杂,给发动机建模与控制研究带来困难。针对RBCC发动机的地面直连实验构型,采用三维CFD计算分析RBCC流场特点,研究发动机状态变量特征,并基于CFD计算结合拟合法的建模思路,建立了RBCC状态空间模型,模型的计算结果与三维CFD的计算结果有较好的吻合度,均方差满足要求。研究表明,在一定范围内增加计算特征数据点个数,可提高建模精度,但当计算特征数据点的个数超过20时,继续增加点的个数对精度的提高非常有限。
RBCC;CFD方法;建模;模型辨识
0 引言
火箭基组合循环(Rocket Based Combined Cycle,RBCC)发动机将火箭发动机的高推重比和吸气式发动机的高比冲等优点有机地组合在一起,在不同的飞行马赫数区间,利用最有效率的热力循环模式进行工作,使推进系统的性能保持全工作过程最佳,且发动机结构简单,成本较低,具有较好的发展前景[1]。RBCC发动机工作过程主要经历4种模态:火箭引射模态、亚燃冲压模态、超燃冲压模态及纯火箭模态,来流条件跨度较大,气动热力过程复杂,必须对发动机的燃烧组织进行主动控制,以实现宽范围内高效稳定的燃烧。现阶段主要通过切换喷注位置和变化燃料当量比来组织燃烧,实现燃烧模态的控制需要建立能反映喷注位置和燃料当量比变化对发动机性能影响的状态空间模型。本文探讨RBCC发动机模型的形式与状态变量选取原则,并进行建模研究。
目前来看,RBCC发动机性能模型发展水平远不如双模态超燃冲压发动机,后者一维模型较普遍[2]。这主要因为没有火箭燃气射流,且发动机相对结构简单,只有一个略有扩张的直通道,分析过程易于简化[3],一维模型已经达到了较高的计算精度。与双模态超燃冲压发动机相比,RBCC发动机由于存在一次火箭,构型更加复杂,且RBCC发动机工作范围更宽,来流条件变化大,流动、燃烧的不稳定性更加突出,建模的难度更大。与双模态超燃冲压发动机类似,RBCC流动燃烧过程中,存在燃烧室截面面积变化、燃料质量添加、放热、摩擦力等驱动力,液态燃料蒸发过程、隔离段内斜激波串结构等作用因素,但RBCC的火箭支撑结构及支板组、凹腔组和直扩通道的多重变化,使RBCC流道截面积变化形式更加复杂,且火箭燃气射流与空气流之间存在强梯度剪切流,引起强烈的动量与能量交换,使流动燃烧机理愈加复杂。此外,兼顾引射、亚燃和超燃多模态燃烧组织和性能提升的要求,必须采用更加灵活的喷油规律,致使喷油位置和喷油数量变化范围极大。这些特点使发动机流动、燃烧的CFD数值模拟难度加大。可想而知,要获得高精度、宽适应性的简化一维模型面临的困难。此外,必须根据RBCC流动燃烧特点,研究RBCC状态变量形式和特征截面位置,以适应RBCC多模态工作控制需求。
文献检索发现,尚未有RBCC状态空间模型研究的报道,RBCC一维模型目前也主要为美国的SCCREAM性能分析模型和国内吕翔等建立的准一维稳态性能分析模型。SCCREAM报道最为公开,它采用常微分方程,由入口沿着流动方向步进求解。但从特征线理论来看,该方法只适用于超燃模态,对于引射和亚燃模态,无法考虑反压对燃烧室性能的影响,且引射模态引射能力的计算问题也没有得到解决[4]。西北工业大学的吕翔[5]、张时空等[6]建立的准一维性能分析模型,通过Mac Cormack格式进行求解,考虑了加质、变截面、摩擦、化学反应源项的影响,解决了上述方法的不足,能够适用于引射/亚燃/超燃/火箭各个模态下RBCC发动机性能的计算。结果表明,对于特定构型的发动机,在一定来流条件下,采用一维性能分析模型与实验结果有较好的吻合度,但当构型复杂或来流条件变化较大时,需要提高模型的适应度。同时,该模型基于稳态计算,实际需要的动态过程模型还须研究燃油蒸发、混合及化学反应与流道边界层及复杂波系的综合作用过程,能用于动态计算的一维简化模型还需时日。
数值计算的发展带来了研究问题的新思路,三维CFD可提供整个流场的信息,利用CFD进行控制系统建模的方法已在国内外不同领域得到成功应用。美国航天局的刘易斯研究中心在进行高超音速飞行器控制系统的设计时,首次将CFD与控制理论进行了结合,以CFD计算来提供流场信息,最终建立了控制系统的线性模型[7];国内孟庆龙等为实现空间温度系统的建模与控制,以CFD对被控对象进行数值模拟,为系统辨识和控制提供全场时空信息,并将参数估计和控制算法嵌入CFD数值计算中,实现了基于CFD的系统建模和闭环控制[8]。因此,在现阶段简化模型发展不足的现状下,基于试验验证过的CFD计算,可期望用于开展发动机状态空间模型研究。
本文采用三维CFD结合拟合法的方法,对RBCC发动机地面直连试验构型建立了状态空间模型,并在matlab的simulink工具箱下,搭建仿真模型,对结果进行验证;另外,还对计算特征点个数与均方差的变化关系进行了研究。
1 三维CFD计算与流场分析
1.1 模型与验证
状态空间模型的建立,需要获取RBCC发动机工作的动态响应数据,即RBCC发动机在特定输入信号下,参数随时间的变化关系。因此,必须对RBCC发动机进行非稳态数值计算,并保存工作过程中特性参数的变化。
三维CFD计算的发动机构型如图1所示,主要包括设备喉道、隔离段、一次火箭、燃烧室和尾喷管。本文的研究对象为地面直连实验发动机,工作中以设备喉道来模拟来流状态。燃油喷注选用支板与壁面组合的两点喷注方案,喷注位置见图1的Wf1和Wf2。
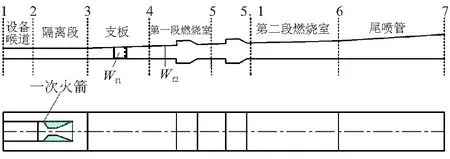
图1 RBCC发动机截面图
计算工具选用商用软件fluent,控制方程为三维非定常雷诺时均化N-S方程,采用有限体积法求解多组分带化学反应湍流燃烧流动问题。对流项采用二阶迎风格式,粘性项采用二阶中心差分格式。选取k-ωMenter SST模型为湍流模型,对自由剪切层及分离流动具有较好的计算精度,在计算燃烧、流动问题上具有一定优势。液态煤油的成分较为复杂,化学反应机理十分复杂。
考虑到计算效率与规模,本文的数值模拟中,采用C10H16作为煤油代用分子式,采用6组元3步化学反应的Arrhenius有限速率模[9]。煤油液滴喷射模型为拉格朗日两相流模型,液滴破碎模型为TAB模型。三维CFD计算结果的有效性在潘科玮、徐朝启的研究工作中已得到了验证[10-12],他们对亚燃模态和超燃模态多种来流工况三维CFD的计算结果与实验结果进行了对比。结果证明,三维CFD能够较好地反映流场的实际状况,可用于RBCC发动机动态参数的获取和流场特性的分析。
1.2 流场特点与热力喉道形态
一次火箭作为RBCC发动机的特色,其富燃高温的火箭羽流不仅可作为发动机二次燃烧的点火源,还与主流空气掺混、物质输运并进一步燃烧,氧气和燃烧区域之间的物质交换得到增强,高温区域不断扩大,火焰拥有更强的传播能力。RBCC发动机采用支板与凹腔组合进行火焰稳定。从图2可看出,支板后形成的混合增强区域与凹腔形成的剪切层火焰稳定区域连成一体,火焰稳定燃烧区域进一步扩大,区域中的传质传热得到加强,燃烧反应进行得更加完全。
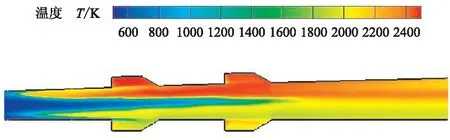
图2 凹腔与支板形成的高温区域
热力喉道在发动机的工作过程中发挥着重要作用,它可避免复杂的作动机构,在低速条件下,实现气流的壅塞和膨胀加速做功,是RBCC发动机实现性能和兼顾各个模态的关键。热力喉道的形态是对发动机工作特性的重要反映。
图3给出了同一构型下,来流Ma=2.5和Ma=4.5的热力喉道分布[13]。
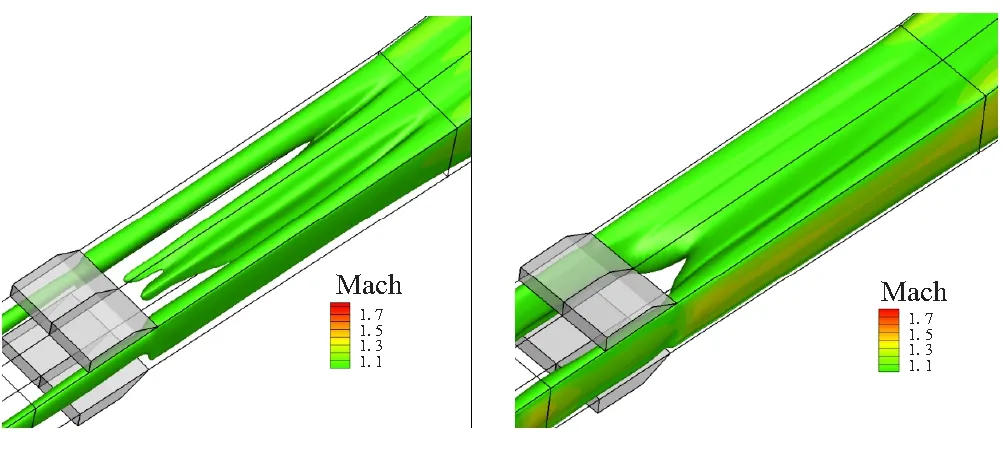
(a) Ma=2.5 (b) Ma=4.5
从图3可看到,热力喉道的分布为三维空间几何曲面,不同来流条件下,热力喉道的形态不同,凹腔组的结构形式、燃料喷射和发动机截面面积变化等因素,对热力喉道的形态也会带来影响,但形成位置基本位于第二级凹腔组之后较近的区域[13]。凹腔在热力喉道形成中具有关键作用,且利用凹腔组对热力喉道形成区域进行控制,对燃烧室也具有较好的适用性。
2 状态空间模型形式
对图1所示发动机建立状态空间模型。在进行状态变量选取和特征截面的确定时,必须使选取的参量能够代表发动机的工作状态,即对发动机工作状态的变化较为敏感,表现在响应参数的幅值相比稳态点有较大程度的变化,同时出于控制考虑,参数应该可测。考虑热力喉道对发动机工作过程的影响,其生成位置应作为监测的特征截面。由于热力喉道的生成位置靠近第二级凹腔组,因此选取靠近热力喉道位置的截面5.1处压强作为状态变量1,记为p5.1。同时,从能量转换角度的来看,燃烧放热在第二段燃烧室就已经基本结束,截面6至截面7部分为膨胀加速段。因此,中间部分的压强均可表征发动机的燃烧放热情况,这里选取截面7处压强为状态变量2,记为p7。本文不考虑一次火箭与第一段燃烧室之间各截面,虽然一次火箭在发动机的燃烧组织中发挥着重要的作用,但一次火箭之后,截面的压强作为状态变量并不能反映二次燃料的喷注与燃烧带来的影响,且截面3与截面4之间波系复杂,一次火箭的富燃羽流与来流空气剪切作用强烈,带来的动量与能量交换使得压强受到较多因素的影响,具有更多的不确定性。
为提高计算精度,本文以设备喉道出口截面的平均压强p2为基准,对压强做归一化处理。实际上,只要设备喉道不被破坏,p2将保持不变。最终选取x=[Φ1Φ2]′为系统的状态变量和输出变量,Φ1=p5.1/p2,Φ2=p7/p2,p5.1和p7分别对应截面5.1和截面7与侧壁面交线中点处压强。以u=[Wf1Wf2]′为系统的输入,其中Wf1为支板的喷油量,Wf2为壁面的喷油量。根据所选的输入、输出与状态变量,最终建立的系统状态变量模型如下:
(1)
3 模型辨识
以拟合法对模型进行辨识,即通过三维CFD计算获得非线性动态响应数据之后,以线性动态响应和非线性动态响应相互吻合为建模原则,建立一组非线性方程;最后通过对方程组的求解,确定状态空间矩阵中的各元素。不失一般性,设该线性系统有两个互异模态:es1t和es2t,则有
s1+s2=a11+a22
s1s2=a11a22-a12a21
(2)
设支板的燃油喷注量做阶跃ΔWf1=δWf1,ΔWf2=0,则线性动态响应为[14]
(3)
设壁面燃油的喷注量做阶跃ΔWf2=δWf2,此时ΔWf1=0,则线性动态响应为[14]
(4)
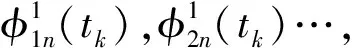
(5)
将式(5)与式(2)联立,可得到包含4K+2个非线性方程的非线性方程组,其最小二乘解即可确定状态变量模型矩阵中的各个元素。在对方程组进行求解时,以matlab作为求解工具,利用lsqnonlin函数,通过Leveberg-Marquardt方法进行一维搜索。在对初值进行选取时,可通过试算,对初值进行预估[15],初值选定之后,经过反复迭代,最终获得结果。
4 举例
以RBCC亚燃模态典型的Ma=3来流工况为例,给出具体的建模过程。
动态计算选择Ma=3来流工况的稳态计算结果,作为起始计算工作点。其中,支板喷注量为220 g/s,壁面喷注量为0 g/s。对两者的燃油喷注量分别阶跃之后,进行三维非稳态数值计算。
计算工况点:
(1)支板燃油喷注阶跃110 g/s,即支板喷注量为330 g/s,壁面喷注量为0 g/s;
(2)壁面燃油喷注阶跃110 g/s,即支板保持喷注量220 g/s不变,壁面喷注量变为110 g/s。
选取计算工况点1和2的动态数据进行拟合计算,暂选取20个特征数据点。最终可得到由82个非线性方程组成的非线性方程组,其最小二乘解即为待求系数矩阵,这样计算得到的状态变量模型矩阵为


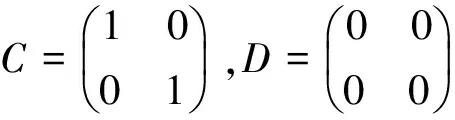
为了分析线性系统对三维CFD所得到动态数据的拟合精度,这里以simulink工具箱为基础,搭建了图4所示的仿真模型。输入为2个不同的阶跃信号,分别对应支板与壁面喷注油量的阶跃,计算采样时间间隔设置为0.4 ms,输出1和输出2分别记录p5.1和p7的压力变化情况。
将计算所得状态空间矩阵代入上述仿真模型,通过计算,获得RBCC发动机的线性动态响应参数。将结果与三维CFD的计算结果进行对比,对比结果如图5、图6所示。其中,1代表监测点p5.1的压力变化曲线;2代表发动机出口截面压强p7的变化曲线。
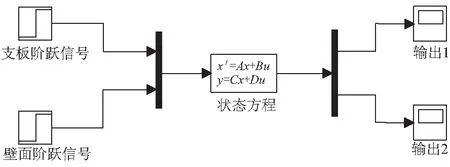
图4 Simulink工具箱的仿真模型
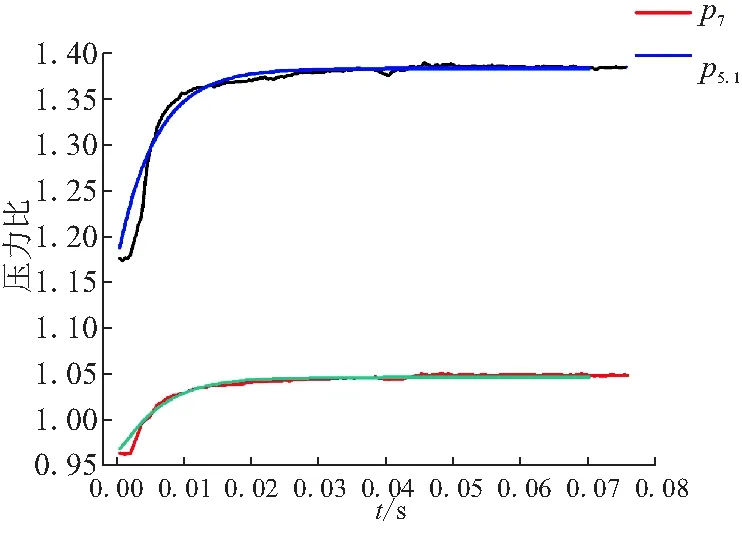
图5 支板阶跃压力响应曲线对比
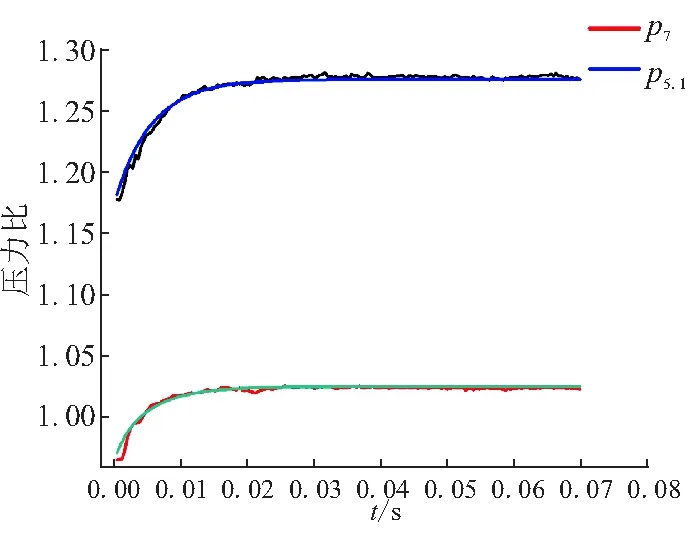
图6 壁面阶跃压力响应曲线对比
从图5、图6可看到,模型的计算结果与三维CFD的计算结果吻合度较好,在误差允许的范围内,可用模型的计算结果近似替代三维CFD的非线性动态响应结果。为定量化评估对比效果,现对模型计算结果的均方差进行计算,表1给出了均方差的计算结果。
从表1可看到,各曲线的均方差都在10%以下,这满足建模的需求和实际控制工作的需要,证明拟合法可用于RBCC控制系统模型的建立。

表1 20个特征点的均方差计算
为考察计算特征点个数与均方差变化的关系,选择11、15、20、22、25个特征数据点,分别对模型进行辨识。对应所选择的计算特征数据点,分别建立非线性方程组,通过再次迭代求解确定状态空间矩阵。
表2给出了各个特征数据点的计算结果。从表2可看到,当特征点个数小于20时,增加特征点个数使模型精度有较大的提升;当特征点的个数超过20时,再增加特征点的个数对于精度的提升作用不大,且从支板阶跃-p7和壁面阶跃-p5.1可看到,特征数据点的选取应存在一最优值,且对应于不同曲线,最优特征数据点个数不同。超过这个界限之后特征点个数的提升反而带来拟合精度的下降。这是因为超定方程组的最小二乘解的应是满足所有非线性方程的误差之和最小,随着方程组个数的增加,已经具有较优拟合精度的点必然要发生偏离,使得整体拟合精度较好,且方程组个数越多,偏离的应该也越大。同时,方程组个数的增加所带来计算成本的提高,也是必须要考虑的因素。综合考虑,在计算特征数据点的个数取20个较为合适。
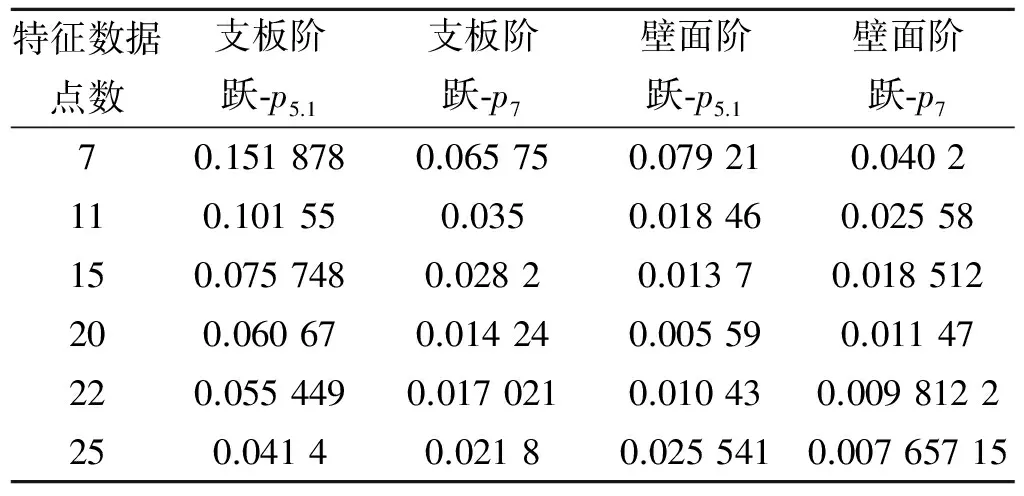
表2 不同特征点数均方差计算汇总
5 结束语
针对RBCC发动机的建模问题,提出了三维CFD计算结合拟合法的建模思路,并以Ma=3来流地面直连实验构型发动机为例,利用三维CFD计算了发动机动态响应特性和流场特性。在此基础上研究了状态变量特征和特征截面的位置,并确定了状态空间模型的形式。最后,利用拟合法对模型进行辨识,并在matlab的simulink工具箱下,搭建了仿真模型,对拟合精度进行了检验。研究表明,模型的计算结果和通过三维CFD的计算结果具有较好的吻合度,说明三维CFD结合拟合法的方法,可用于RBCC发动机模型的建立。研究还发现,当计算特征数据点较少时,可通过增加计算特征点的数量来,提高模型的精度,但当计算特征点的数目达到20时,继续增加特征点数量,对于精度的提高意义不大,且特征点数应有一个最优值,超过最优值反而带来拟合精度的下降。
从研究过程可看到,三维CFD计算提供了发动机的动态特性响应数据,对发动机流动、燃烧过程的研究结果,也决定模型中状态变量的选取。拟合法对动态数据的精度要求较高,三维CFD计算因为可提供整个流场的信息,计算结果较为准确。但动态数据的来源不应局限于三维CFD计算,在保证结果准确可靠的前提下,实验和一维模型都是解决问题的思路。实验是动态数据最直接的来源,在考虑成本的因素下,可和三维CFD计算相互补充。现阶段RBCC一维模型由于发展的不完善,限制了其适用范围,但其作为一种快速预估的手段,相比三维CFD计算的长周期性,一维模型仍具有较好的发展前景,需拓宽其适用范围和提高计算精度,以满足建模需要。
[1] 刘洋,何国强,刘佩进,等.RBCC组合循环推进系统的研究现状和进展[J].固体火箭技术,2009,32(3):288-293.
[2] 曹瑞峰.面向控制的超燃冲压发动机一维建模研究[D].哈尔滨:哈尔滨工业大学,2011.
[3] 张鹏,愈刚.超燃燃烧室一维流场分析模型的研究[J].流体力学实验与测量,2003,17(1):88-92.
[4] 吕翔,刘佩进,何国强.RBCC发动机性能分析方法研究[J].固体火箭技术,2007,30(2):120-123.
[5] 吕翔,何国强,刘佩进.RBCC引射模态准一维性能分析[J].推进技术,2006,27(6):529-532.
[6] 张时空,刘佩进,吕翔.RBCC发动机性能快速分析方法改进和验证[J].固体火箭技术,2013,36(4):468-473.
[7] Chicatellia,Hartleyt Coleg,et al.Interdisciplinary modeling using computational fluid dynamics and control theory[C]//Proceedings of the American Control Conference Baltimore,Maryland,USA:IEEE Press,1994:3438-3443.
[8] 孟庆龙,王元.基于CFD的空间场温度系统建模与控制[J].浙江大学报,2012,46(8):1478-1484.
[9] 潘科玮,何国强,刘佩进,等.RBCC混合燃烧模态一次火箭对燃烧稳定影响[J].推进技术,2010,31(1):544-548.
[10] 潘科玮,何国强,秦飞,等.用小支板及凹腔组合提高火箭冲压组合发动机的燃烧性能[J].推进技术,2012,33(2):216-220.
[11] 徐朝启,何国强,秦飞,等.基于直扩流道构型的RBCC发动机亚燃模态高效燃烧组织演技[J].推进技术,2014,35(4):507-513.
[12] 徐朝启,何国强,秦飞,等.基于气化煤油喷注的RBCC燃烧室亚燃模态燃烧组织研究[J].推进技术,2013,34(8):1064-1070.
[13] 王亚军,何国强,潘科玮,等.RBCC亚燃模态热力喉道机理的数值模拟[J].推进技术,2013,34 (7):932-937.
[14] 冯正平,孙健国,黄金泉,等.一种建立航空发动机状态变量模型的新方法[J].航空动力学报,1998,13(4):435-438.
[15] 陆军,郭迎清,陈小磊.线性拟合法建立航空发动机状态变量模型[J].航空动力学报,2011,26(5):1172-1177.
(编辑:崔贤彬)
Modeling method of RBCC engine based on three-dimensional CFD
PAN Hao,PAN Hong-liang,QIN Fei,HE Guo-qiang,WANG Ya-jun
(Science and Technology on Combustion,Internal Flow and Thermo-Structure Laboratory,Northwestern Polytechnical University,Xi'an 710072,China)
RBCC engine can operate at multi-modes((inject-,ramjet,scramjet and rocket as well))and adapt to a wide flight envelope,which is mainly resulted from the shearing action between the primary rocket plume and inlet air varies drastically.The cross-section along the flow path varies a lot for mounting the rocket,stabling the burning and accelerating the gases, and meanwhile the fuel is injected changing in both the amounts and the positions as well according to the operating mode.The complex driving-forces result in the difficulties to develop the performance model and to control RBCC.Based on the ground test configuration of RBCC engine,the characteristics of flow field and state variables of RBCC engine were studied by using three-dimensional CFD,and then a state variable model with the method of CFD and linear fitting was developed.It is shown that the state variable model matches up with CFD calculations. Studies also show that modeling accuracy can be improved by increasing the data points till 20.
RBCC; CFD method;modeling;model identification
2014-06-30;
2014-07-24。
潘浩(1990—),男,硕士,研究方向为航空宇航推进理论与工程。E-mail:panhao@mail.nwpu.edu.cn
V435
A
1006-2793(2015)03-0336-06
10.7673/j.issn.1006-2793.2015.03.007
