扩散与幂率蠕变联合控制的孔洞受约束长大模型研究

刘 旻，王 冲，郭晓峰，巩建鸣

(1.南京扬子伊士曼化工有限公司，南京 210048;2.内蒙古科技大学 机械工程学院，内蒙古包头 014010；3.南京工业大学 机械与动力工程学院，南京 211816)

0 引言

高温环境下，材料的变形与断裂的微观机制主要是晶界的孔洞化。当蠕变进入第三阶段后，蠕变逐渐加速并最终发生断裂，材料的破断过程主要表现为晶界孔洞的形核、长大和合并[1-2]。一般而言，孔洞容易在晶界处形核。相关研究发现[2-8]，孔洞可以在晶界处的多个位置形核，如在夹杂物、第二相粒子、晶界坎和三叉晶等晶界结构不规则处。目前，普遍认为蠕变过程中晶粒之间的滑移在晶界不规则处受阻而产生的应力集中是孔洞形核的主要原因。对于孔洞形核机制，已有许多学者提出了相应的理论，这些理论可以对某一类材料的断裂机理给出合理的解释，但是对其他材料却不再适用。在很多情况下，对于特定合金的形核机制仍不完全清楚。

在过去的几十年间，孔洞的长大问题得到大家的广泛关注。HULL等[9]基于空位扩散理论，率先提出了空位沿晶界扩散到孔洞的扩散控制孔洞长大模型(H-R模型)。但是该模型存在一个严重缺陷，即孔洞数恒定的假设，这与断裂时间强烈依赖于试验应力的客观事实不一致。为了解决H-R模型的问题，SPEIGHT等[10]将空位浓度引入Fick第二定律，提出了另一种形式的扩散控制孔洞长大模型(B-H模型)。在此基础上，BEERE等[11]通过考虑蠕变变形对空位扩散产生的影响，进一步提出了扩散与蠕变联合控制的孔洞长大模型(B-S模型)。此后，CHEN等[12]在晶界扩散和蠕变耦合的基础上，考虑了孔洞表面扩散的影响，提出表面扩散、晶界扩散和幂率蠕变相耦合的孔洞长大模型(C-A模型)。值得注意的是，蠕变过程中孔洞的长大是一种非常复杂的行为，很多因素会对孔洞的长大产生影响。目前，虽然许多学者提出了一些相对合理的孔洞长大模型，但这些模型中考虑影响孔洞长大的因素还不够全面。基于此，以国产蒸汽转化炉集气管用20Cr32Ni1Nb钢为研究对象，建立扩散和幂率蠕变联合控制的孔洞受约束长大模型，并将模型的预测结果与Needleman-Rice模型和Chen-Argon模型进行比较。

1 模型的构建

在晶粒发生蠕变变形的情况下，晶界上空位的生成和扩散是不均匀的。空位主要在孔洞附近区域生成和扩散，其他区域通过幂率蠕变变形协调导致原子沉积而引起晶粒滑移。以轴对称孔洞及围绕它的基体为研究对象，模型示意如图1所示。

图1 扩散和幂率蠕变联合控制的孔洞受约束长大模型示意Fig.1 Schematic diagram of a cavity growth modelcontrolled by combined diffusion and power law creepdeformation under constrained condition

基体在远场应力σ∞作用下发生幂率蠕变，作用于晶界的正应力σ如图2所示。

图2 模型中晶界正应力分布Fig.2 Normal stress distribution acting on grainboundaries in the model

模型中，孔洞之外的区域分成扩散区(Ⅰ)和蠕变区(Ⅱ)。其中，在扩散区Ⅰ内，空位生成并扩散到孔洞，使孔洞长大；而在蠕变区Ⅱ内不产生空位，该区域通过蠕变变形来协调扩散区原子沉积引起的位移。如图2所示，在孔洞表面处的应力为2γs/R，孔洞扩散要求在扩散区域Ⅰ内作用于晶界的正应力随任意孔洞半径r的增加逐渐升高。当r≥b时，应力梯度为0，即不发生空位扩散。模型中，晶界长度为d，孔洞半径为R，孔洞之间间距为2b，并且b等于孔洞中心的扩散控制距离，Λ是有效扩散控制距离，CHEN等[12]将其定义为:

(1)

实际中，当(R+Λ)≥b时，Λ=b。

1.1 表面扩散

在孔洞表面处，孔洞上下两个表面上扩散的原子在孔洞顶端(孔洞与晶界的交界处)汇合后继续沿晶界扩散。若孔洞顶端处的表面扩散流量为Js，根据质量守恒关系，孔洞的体积长大速率可表示为:

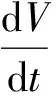
(2)

式(2)中孔洞顶端处的表面扩散流量Js与孔洞形状有关。对于球形孔洞和裂纹形孔洞，CHUANG等[13]研究指出表面扩散流量Js分别为:

(3)

(4)

其中：

(5)

式中，h(Ψ)为孔洞顶端张开半角的函数；Ds为表面扩散系数；δs为表面层厚度；γs为表面能。

1.2 晶界扩散与蠕变的耦合

在扩散区Ⅰ内，由于空位的化学位与应力成正比，BEERE等[11]指出可以用扩散区的应力σ代替扩散方程中的化学位，即:

(6)

式中，α为单位时间内单位面积上沉积的原子数，即单位面积原子沉积速率。

求解式(6)，得:

(7)

式中，A和B为待定常数，可根据以下边界条件确定A，B和α的值。

(8)

(9)

(10)

根据第2个边界条件(即式(9))可以确定α的值:

(11)

将式(11)代入式(7)，得:

(12)

利用式(8)(10)可以确定A和B，即:

(13)

(14)

同时，将孔洞体积长大速率用原子沉积速率来表示，即:

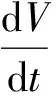
(15)

将式(11)(13) 代入式(15)，得:

(16)

将式(1)代入式(16)，并采用OGATA[14]的方法，用σ代替σⅠ-2γs/R，则:

(17)

(18)

将式(17)代入式(18)，有:

-R4/(4b4)+R2/b2-3/4]}-1

(19)

此外，RICE[15]在研究蠕变孔洞的受约束长大问题中，得出:

(20)

式中，β为材料常数。

将式(19)与式(20)联立，得：

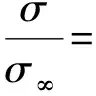
(21)

将式(21)代入式(17)，得：

(22)

本模型中，由于空位(或原子)只在R≤r≤R+Λ区域内扩散，所以用(R+Λ)代替式(22)中的b就可以表示扩散与蠕变耦合情况下的孔洞受约束长大速率，即:

(23)

其中:

(24)

(25)

最后，根据质量守恒定律，扩散与蠕变耦合条件下受约束孔洞长大速率等于孔洞顶端原子扩散所导出的孔洞长大速率，即将式(2)～(5)与式(23)联立，得到如下公式。

球形孔洞的长大速率为:

(26)

裂纹形孔洞的长大速率为:

(27)

其中：

(28)

2 模型参数的确定

以国产蒸汽转化炉集气管用20Cr32Ni1Nb钢为研究对象，孔洞长大速率计算过程中采用的材料参数如表1所示。

表1 孔洞长大速率模型的材料参数Tab.1 Material parameters of the cavity growth rate model

3 结果与讨论

蠕变过程中孔洞长大是一种非常复杂的行为。考虑到理论研究和工程实际的重要性，各国学者对孔洞长大的微观过程及机制进行了大量的研究，并提出了许多孔洞长大的模型，主要包括扩散控制的孔洞长大模型(Diffusion controlled model)[9-10,13,16]、扩散控制的孔洞受约束长大模型(Diffusion controlled considering constraint effect model)[15]、扩散和蠕变耦合控制的孔洞长大模型(Diffusion and power law creep deformation controlled model)[11-12]。本文提出了扩散和蠕变耦合控制的孔洞受约束长大模型，该模型可以预测球形与裂纹形孔洞的长大速率。

基于CHEN等[12]的研究，假设蠕变过程中孔洞的形状是由某一状态下球形和裂纹形孔洞的长大速率决定的。当球形孔洞的长大速率高于裂纹形孔洞时，孔洞以球形长大；反之，则孔洞以裂纹形长大。由于式(26)(27)分别表示球形孔洞和裂纹形孔洞的长大速率，故将两式联立即可得到从球形孔洞向裂纹形孔洞转变所对应的临界孔洞半径Rc。图3所示为球形孔洞长大速率与不同λ值所对应的裂纹形孔洞长大速率的关系图。从式(28)中可以看出，λ是与晶界扩散速率和表面扩散速率之比相关的参数，不同的λ值可以反映不同的裂纹形孔洞的长大速率。图3中的交点即为不同λ值所对应的球形孔洞向裂纹形孔洞转变的临界孔洞半径。随着λ值的增加，球形孔洞向裂纹形孔洞转变所需的临界孔洞半径Rc逐渐减小。

图3 球形孔洞长大速率与不同λ值所对应的裂纹形孔洞长大速率的关系(Λ=10-6 m)Fig.3 Relation between growth rates growth rate ofspherical-shaped cavity and crack-like cavity withdifferent values of λ(Λ=10-6 m)

在试验条件下，孔洞长大速率与孔洞半径之间的关系如图4所示。当孔洞半径小于1 μm时，由于孔洞的表面扩散速率与晶界扩散速率相平衡，孔洞以球形孔洞长大。当孔洞半径大于1 μm时，裂纹形孔洞的长大速率比球形孔洞更快，表明与表面扩散相比，这一阶段晶界扩散更加显著。在晶界扩散的作用下，球形孔洞逐渐向裂纹形孔洞转变，这一计算结果与试样观测的孔洞长大过程一致。此外，从图4中还可以看到，使用应力增大时，孔洞形状转变的临界半径减小。这主要是由于应力增加时有效扩散范围减小，即晶界扩散的作用增大，因此从球形孔洞向裂纹形孔洞转变的临界半径减小。同时，试验温度的升高也会对球形孔洞向裂纹形孔洞的转变产生加速作用，如图4所示。

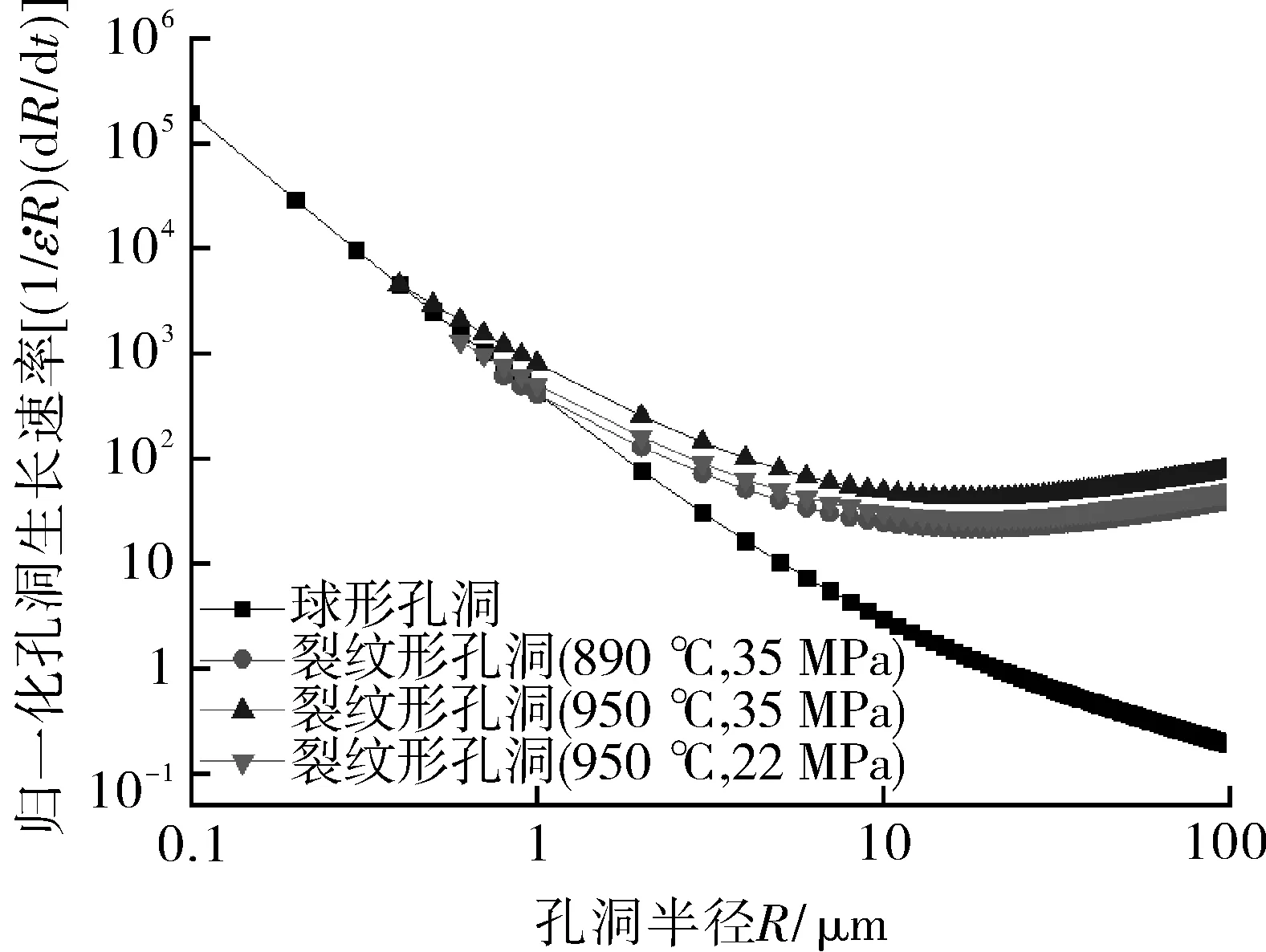
(a)Λ=10-5 m (b)Λ=10-6 m

在温度890 ℃和950 ℃，应力在10～60 MPa的条件下，Λ值一般在10-6～10-5m之间。为了便于模型之间的对比，本研究中Λ分别取10-6m和10-5m进行孔洞长大速率的计算。图5对比了基于Needleman-Rice模型(孔洞扩散长大模型)[16]、Chen-Argon模型(扩散与蠕变耦合控制孔洞长大模型)[12]和本文提出的扩散和蠕变耦合控制的孔洞受约束长大模型所计算出的孔洞长大速率。可以看出，无论是球形孔洞还是裂纹形孔洞，与Needleman-Rice模型相比，基于Chen-Argon模型和本文提出的模型计算出的孔洞长大速率明显更大。当Λ=10-5m时，有效扩散距离Λ大于孔洞间距b，孔洞长大速率主要由扩散控制。在这种情况下，由于幂率蠕变对孔洞的影响与扩散作用相比可以忽略，基于3种模型计算得到的孔洞长大速率结果基本相一致，如图5(a)所示。同时，本文提出的模型计算的孔洞长大速率略低于未考虑约束效应的Chen-Argon模型。当Λ=10-6m时，有效扩散距离Λ小于孔洞间距b。此时，幂率蠕变会对孔洞长大产生很大的影响。从图5(b)可以看出，基于本文提出的模型比仅考虑扩散作用的Needleman-Rice模型计算出的孔洞长大速率要高，但由于考虑了约束效应，又比Chen-Argon模型计算出的孔洞长大速率低。当孔洞半径等于孔洞间距时，基于Needleman-Rice模型预测的孔洞长大速率逐渐接近Chen-Argon模型和本文提出模型的计算结果。综上所述，基于本文提出的模型预测的孔洞长大速率与基于Needleman-Rice模型和Chen-Argon模型的计算结果基本相一致；与不考虑约束效应的Chen-Argon模型相比，基于本文提出的模型所计算的孔洞长大速率较低。

(a)Λ=10-5 m (b)Λ=10-6 m

4 结语

蠕变过程中孔洞的长大是一种非常复杂的行为，很多因素会对孔洞的长大产生影响。目前虽然许多学者提出了一些相对合理的孔洞长大模型，但这些模型中考虑影响孔洞长大的因素还不够全面。本文基于扩散和幂率蠕变耦合控制孔洞长大理论，建立了新的孔洞受约束长大模型，该模型预测的孔洞长大速率与基于Needleman-Rice模型和Chen-Argon模型的计算结果基本相一致；与不考虑约束效应的Chen-Argon模型相比，基于本文提出的模型所计算的孔洞长大速率较低。