带落角约束的固定配平攻角飞行器滚转制导律设计

耿克达，周 军，林 鹏

(西北工业大学 精确制导与控制研究所，西安 710072)



带落角约束的固定配平攻角飞行器滚转制导律设计

耿克达，周 军，林 鹏

(西北工业大学 精确制导与控制研究所，西安 710072)

固定配平攻角飞行器具有外形简单、控制通道少的优点，但其升力大小不可控，为实现精确制导，解决其带终端角度约束制导的问题，提出了一种含虚拟目标的滚转制导律设计方法。建立了含虚拟目标的滚转制导方程，给出了基本导引关系，并证明了该导引关系下设计的制导律能有效对飞行器落点与落角进行控制。同时，给出了虚拟目标详细设计方法，并通过数值仿真验证了该制导律的有效性。仿真结果表明，提出的含虚拟目标的滚转制导律设计方法具有较高的制导精度与落角精度，同时设计方法简单，便于工程应用。

固定配平攻角飞行器；落角约束；虚拟目标；滚转制导

0 引言

再入飞行器机动飞行可有效规避拦截系统拦截，同时提高落点精度。可实现机动飞行控制的再入飞行器气动外形有十字舵外形、可变攻角BTT外形及固定配平攻角外形[1-2]。其中，固定配平攻角外形采用单通道控制方式，利用再入飞行器的外形不对称或质心偏移产生不可控的配平攻角，通过滚转改变配平升力的方向，实现机动飞行，其典型代表是美国的MK500逃逸型机动再入体[3]。相比于前两种外形，固定配平攻角外形的再入飞行器具有外形简单、控制通道少的优点。

随着飞行技术的发展，飞行器不仅希望获得最小脱靶量，还希望以最佳姿态命中目标，从而达到最佳作战效能。文献[4]研究了带落角约束的变结构制导律，并分析了滑模参数对制导性能的影响；文献[5]采用落角控制导引律，通过引入开关控制项，解决了大落角飞行下目标超出导引头视场的问题。此外相关文献还研究了带落角约束的比例制导、最优制导等方法[6-8]。然而，这些方法都是将飞行器运动分解到纵、侧两个平面，独立设计各向所需过载，并使飞行器过载指向与其重合，从而保证落点与落角精度。对于固定配平攻角再入飞行器，由于其升力大小不可调节，在再入体接近目标时，出现升力多余，若仍采用上述方法，滚转指令将发生快速换向切换，这一方面导致落点精度不高，同时不利于控制系统设计与实现[2]。

为此，Gracey和Cliff提出一种控制再入体滚动来消耗多余升力，并最终实现精确制导的滚转制导方法[9]。这种方法通过引入一个空间误差角σ，得到了飞行器空间单平面制导方程，之后利用倾侧角γv控制σ收敛于零，从而实现精确制导。虽然这种方法不可避免地存在方法误差，但仍然具有较高的制导精度。可是在这种制导方式下，无法对飞行器落地姿态进行有效控制。国内李自行将Gracey等的方法应用于再入飞行器六自由度模型中，分析了滚转制导方法误差产生的原因及制导系数k对落点精度和滚转速度的影响[10]，仍然没有解决飞行器落角约束的问题。为此，Robert采用在线离散弹道规划[11]，设计了固定配平攻角再入飞行器制导指令，但这种方法精度不高，实现复杂，工程应用难度较大。

虚拟目标制导是一种新的实现落角约束的制导方法[12-13]，通过引入具有一定运动规律的虚拟目标，结合传统的制导方法，不需改变制导律形式即可对飞行器落角进行有效控制。因此，针对固定配平攻角再入飞行器含落角约束的制导问题，本文提出了一种带有虚拟目标的滚转制导律设计方法。利用滚转制导律解决飞行器升力多余的问题；利用虚拟目标导引飞行器实现最终的落点与落角约束。

1 含虚拟目标的滚转制导律设计

本文以一种外形不对称再入飞行器为研究对象，该外形飞行器具有如下特点[10]：

(1)俯仰、偏航通道具有自稳定性，不施加主动控制；

(2)稳定飞行条件下，飞行器攻角为不对称外形产生的固定配平攻角α=α*，侧滑角β=0；

(3)在气动偏差情况下，俯仰、偏航通道依然自稳，仅配平状态发生变化。

1.1 飞行器质心运动学模型

在圆球地球模型下，忽略地球自转引起的离心惯性力，飞行器质心运动模型如式(1)所示：

(1)

式中 (V，θ，ψv)T为飞行器相对再入系E的相对速度、弹道倾角与偏角；(x，y，z)T为飞行器位置在再入系下的投影；-D、L分别为飞行器本体所受阻力与升力；(gx，gy，gz)T、(fkx，fky，fkz)T分别为引力加速度和地球自转产生的柯氏加速度在弹道系下的投影。

(fkx，fky，fkz)T=(0，-2ωezV，2ωeyV)T

(2)

式中ωey、ωez为地球自转角速度在弹道系下的投影。

1.2 含虚拟目标的滚转制导模型

假设实际目标为固定点OT，选取虚拟目标点为O′并沿过OT的直线运动。三维空间下含虚拟目标的滚转制导如图1所示。其中，飞行器相对再入系的速度矢量为V；虚拟目标相对再入系的速度矢量为Vt；OXYZ为弹道系T，OX′Y′Z′为误差系W，并定义OX′轴与速度矢量重合，其与弹目视线的夹角为误差角σ(0≤σ≤π)，OY′轴在平面XOr内且由OX′轴指向弹目视线r，OY轴与OY′轴的夹角为φ，升力L与OY轴夹角为速度倾侧角γv，且规定从O点顺OX轴看顺时针转动形成的φ、γv为正，反之为负。

图1 滚转制导示意图

弹目视线矢量r在误差系中的投影为

r=(rcosσ，rsinσ，0)T

(3)

将r在误差系求导：

(4)

式(3)中各矢量表达式如式(5)所示：

(5)

联立式(3)～式(5)，并结合方程(1)，可得

(6)

式(6)即为含有虚拟目标的滚转制导模型。当虚拟目标选为固定点OT且采用水平大地模型时，便可得到文献[2，9]中的滚转制导方程，可见其为本文推导的滚转制导模型的一个特例。

1.3 滚转制导律设计

结合式(6)可知，由于升力L不可控，若能通过调节倾侧角γv，控制误差角σ收敛至零[10]，则可实现飞行器速度指向虚拟目标点，并最终实现飞行器与虚拟目标成尾追状态。下面对其进行证明。

令：

(7)

式中K为制导系数。

引理1[2]

在式(7)成立、K>1、V>0及σ的初值不等于π等条件成立的情况下，在任何初值条件下，制导方程组(6)的解都能满足(σ→0，r→0)。

引理2[14]

设有任意非线性系统：

(8)

引理1、2的证明可参考文献[2，14]。

定理1

假设虚拟目标做直线运动，其速度与弹目视线夹角为目标误差角σt(0≤σt≤π)，如图1所示，在引理1满足的情况下，有

σ→0，σt→0

(9)

即飞行器与虚拟目标最终将成尾追状态。

证明：在引理1满足条件下，将式(7)代入式(6)第二式，有

(10)

取Lyapunov函数：

(11)

对其求导：

(12)

因此误差角σ渐近收敛至0。

对于目标速度误差角σt，有

(13)

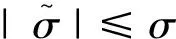
(14)

(15)

有

(16)

即σt也渐近收敛至0。

因此，由引理2可知，(σ，σt)渐近收敛至(0，0)。

证毕。

综上，飞行器与虚拟目标将成尾追状态。然而定理1是基于式(7)成立这一条件的。令：

(17)

式(7)变为

cos(γv-φ)=χ

(18)

由文献[10]可知，实际飞行中，当飞行器接近虚拟目标时，弹目视线距r较小，导致|χ|>1，式(7)不成立。此时飞行器机动能力不足，制导律不再收敛，并最终产生制导方法误差。然而通过合理设计制导系数与飞行速度，可有效减小|χ|>1的时间，进而保证较高的制导精度。

最终可得含虚拟目标的滚转制导指令为

式(19)中各变量均可通过传感器进行直接测量，或者利用数学关系进行求解。

比较式(19)与文献[2]制导律形式可知：此时滚转指令中多出了实现落点与落角约束的虚拟目标运动参数Vtx、Vty以及包含虚拟目标位置信息的弹目视线距γ。下面将对其进行设计。

2 虚拟目标设计

由以上理论可知，若虚拟目标沿某直线运动，当采用式(19)所示的滚转制导律跟踪该虚拟目标时，最终飞行器将与虚拟目标成尾追飞行状态。若该直线过实际目标点且与当地水平面成期望角度，则可对飞行器落点与落角同时进行控制。换言之，飞行器将以固定落角击中实际目标。

2.1 虚拟目标曲线

不失一般性，假设再入时刻飞行器位置为m0，再入系OXe轴指向实际目标t方向，虚拟目标曲线t′t在再入时刻飞行器运动纵平面内，且与当地水平线夹角为期望落角qtf，如图2所示。因此，在再入系下，可得m0与t的地心矢分别为

(20)

图2 虚拟目标曲线示意图

为了求解虚拟目标曲线单位矢量i在再入系下坐标，由几何关系可得

(21)

联立式(20)、式(21)，可得

(22)

2.2 虚拟目标位置与运动速度

为了对飞行器落点进行控制，需保证飞行器与虚拟目标同时命中实际目标，参考文献[13]，使飞行器与实际目标的距离和虚拟目标与实际目标的距离成一定比例，即

r1=cr2

(23)

式中r1为飞行器与实际目标的距离；r2为虚拟目标与实际目标的距离；c为制导系数，设计中应当根据飞行器机动能力水平进行调节，为了保证飞行器与虚拟目标成尾追状态，有c>1。

当制导系数c确定后，则任意时刻虚拟目标位置以及其运动速度可分别确定求解。

由图2可得任意时刻虚拟目标位置地心矢量：

(2)

将式(24)在再入系下求导，并考虑到：

有

(25)

式中σ1为飞行器速度与飞行器到实际目标矢径的夹角。

将式(25)经过2次坐标转换，即可得到误差系下的虚拟目标速度：

Vt=WLTTLEVte

(26)

式中WLT、TLE分别为弹道系到误差系和再入系到弹道系的转换矩阵，其具体表达式不再给出。

将式(26)代入式(19)中，即可得到完整的含虚拟目标滚转制导指令。

3 仿真分析

为验证本文提出的含有虚拟目标的滚转制导律制导性能，以某固定配平攻角再入飞行器为例进行三自由度仿真。

仿真中认为飞行器攻角和侧滑角始终稳定在配平状态，即α=α*，β=0°。假设飞行器再入时刻位于赤道平面内，高度为70 km，速度为5 000 m/s，初始再入倾角和偏角分别为θ0=-2.5°，ψv0=1°，飞行器质量m=300 kg。期望落点在赤道平面内，距再入点地面圆弧长550 km。要求落角小于30°，因此可取虚拟目标曲线过实际目标点，在赤道平面内与当地水平面成45°。

再入初始时刻开启滚转制导，制导系数经调试取为：K=1.3，c=3.5。标称参数下，部分仿真曲线如图3～图6所示。

图3 飞行器三维弹道图

图4 速度倾侧角曲线

由图中曲线可知：

(1)高空段机动能力不足时，根据式(19)，飞行器不进行滚动，而是把升力保留在误差平面内以减小误差角；低空段飞行器通过滚动来消耗多余升力，误差角逐渐减小，保证落点与落角精度。

图5 误差角曲线

图6 当地弹道倾角曲线

(2)飞行器最大滚转角速度约3 rad/s，且方向不存在剧烈切换，有利于控制实现。

(3)落点误差小于1m，落点精度较高。

(4)引入虚拟目标后，飞行器落角振荡收敛至期望落角，振荡周期与飞行器滚转指令周期相同，最终落角误差小于1°。

以标称落点为原点，在其前后15 km内随机选取目标，考虑飞行器气动偏差(最大偏差±10%，不影响飞行器俯仰与偏航通道的自稳定性)、大气密度偏差(最大偏差±10%)和质量偏差(最大偏差±2%)，各项偏差在正负最大值范围内均匀随机取值，图7、图8为500条弹道落点散布图与落角分布图。由图中曲线可知：

(1)各项拉偏下，飞行器落点CEP为3 m，落角误差不大于1.6°。

(2)各项拉偏情况下，含虚拟目标的滚转制导具有较好的制导性能和较强的鲁棒性。

(3)飞行器存在落点与落角偏差很大一部分原因在于制导方法误差，这是由其固定配平攻角外形决定的，具体分析可参看文献[10]。

图7 拉偏情况下飞行器落点散布图

图8 拉偏情况下当地弹道倾角分布图

4 结论

(1)针对固定配平攻角再入飞行器落角约束问题，设计了含直线虚拟目标的滚转制导律，推导了误差平面内含虚拟运动目标的滚转制导模型，给出了虚拟目标及其速度的设计方法，得到了完整的滚转制导律表达式。

(2)含有虚拟目标的滚转制导律具有较高的落点精度、落角精度以及较强的鲁棒性。

(3)含有虚拟目标的滚转制导律设计简单，具有一定的工程应用价值。

[1] Page J A,Rogers R O.Guidance and control of maneuvering reentry vehicles [C]//IEEE Conference on Decision and Control.California,1977:659-663.

[2] 李自行,李高风,黄瑞玲.一种基于固定配平的飞行器滚转制导律研究[J].空间控制技术与应用,2012,38(6):23-26,29.

[3] 谢佐慰.美国机动弹头技术发展概况[J].导弹与航天运载技术,1984(3):3-26.

[4] 胡正东,曹渊,蔡洪.带落角约束的再入机动弹头的变结构导引律[J].系统工程与电子技术,2009,31(2):393-398.

[5] 顾家立,陈万春.一种带导引头视角和落角约束的导引方法[J].宇航学报,2013,34(6):782-787.

[6] 张友安,马培蓓.带有攻击角度和攻击时间控制的三维制[J].导航空学报,2008,29(4):1020-1026.

[7] Mathew Bunn.Technology of ballistic missile vehicles[M].MIT,American,1984.

[8] Roenneke A,Cornwell P.Trajectory control for a low-lift maneuverable reentry vehicle [C]//Aerospace Design Conference.Ervine,CA,1992:1-11.

[9] Gracey C,Cliff E M,Lutze F H,Kelley H J.Fixed-trim reentry guidance analysis[C]//AIAA Guidance and Control Conference.19-21,August 1982.

[10] 李自行,李高风.一种基于不对称再入体的制导与控制方法研究[J].航天控制,2011,29(6):44-48,53.

[11] Robert T Bibeau,David S Rubenstein.Trajectory optimization for a fixed-trim reentry vehicle using direct collocation and nonlinear programming[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.14-17 August 2000.

[12] 顾文锦,张翼飞,王土星.高低巡航弹道中的虚拟目标比例导引[J].海军航空工程学院学报,2000,15(4):425-428.

[13] 顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计[J].飞行力学,2006,24(2):43-46.

[14] Isidori,A.Nonlinear control systems[M].3rd ed.,Springer-Verlag,London,1995:513-515.

(编辑：吕耀辉)

Design of rolling-guidance law using virtual target with control of terminal azimuth for a fixed-trim vehicle

GENG Ke-da，ZHOU Jun，LIN Peng

(Institute of Precision Guidance and Control，Northwestern Polytechnical University，Xi’an 710072，China)

Fixed-trim vehicle with attack angle has the characteristic of simple configuration and less control channels.However,as the magnitude of lift force is uncontrollable,an appropriate guidance law is needed to ensure the guidance accuracy.Thus,in order to solve the guidance problem with the control of terminal azimuth for fixed-trim vehicle,a rolling-guidance law with virtual target was proposed.The rolling-guidance equation with virtual target was established.The basic guidance method was put forward,which is proved that the guidance law could accurately steer the vehicle and control the terminal azimuth effectively.The design method of virtual target was also given and the validity of rolling guidance was analyzed by simulation.The simulation result illustrates that:the rolling-guidance law with virtual target in this paper not only has higher precision of guidance and terminal azimuth control,but also has the simple design,which is convenient for engineering application.

fixed-trim attack angle vehicle；control of terminal azimuth；virtual target；rolling-guidance

2014-05-19；

2014-06-04。

863项目。

耿克达(1985—)，男，博士生，研究方向为导弹及航天器导航、制导与控制。E-mail：gengkeda@163.com

V448

A

1006-2793(2015)03-0320-06

10.7673/j.issn.1006-2793.2015.03.004