老树绽新花，源于灵巧的教学设计

高厚良

[摘 要] 本文简述“陈耀忠工作室”成员门辉老师的“轴对称图形”展示课例，门老师基于教材的理解，与学生一起学习轴对称图形与两个图形成轴对称的相关知识，整节课在设计上，不拘泥于教材，大胆创新，线索分明，对难点的突破有自己的独到之处，引起参会教师的强烈共鸣与广泛思考.

[关键词] 轴对称图形；课例赏析；设计灵巧；双线推进

写在前面

蚌埠市“陈耀忠工作室”部分成员风采展示课期间，笔者有幸领略了安徽省部分优秀教师的精彩展示，对其中的一些课例，尤其是门辉老师执教的沪课版《数学》八年级上册“15.1轴对称图形”情有独钟. 这一课题在安徽省近两届初中数学优质课中都是参评课题，如何在这么多高手的精彩展示后，还能让这棵老树绽放新花，有所突破，成为笔者在听这一课例的期待. 门老师这节课不拘泥于教材，大胆创新，“双线”推进，对难点的突破有自己的独到之处，本节课例展示后，引起参会教师的强烈共鸣与广泛思考. 本文根据本课例的一些精彩片段，做出一些肤浅的赏析，求教于同仁.

精彩回放

精彩片段1：开课阶段

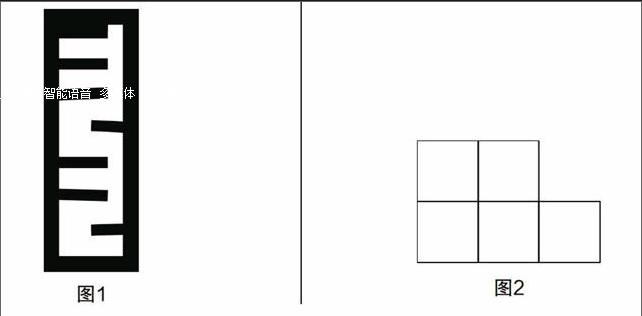
师：（展示红火喜庆的红双喜图案后）我们现在就来剪一剪这个双喜图案好吗？

（教师在讲台演示，学生一边看着老师的演示，一边操作）

师：如果把剪好的双喜图沿着中间这条折痕折叠，会出现什么情况？

生1：重合

生2：折痕两旁的部分完全重合.

师：（多媒体演示折叠双喜图案的过程）像这样的平面图形叫轴对称图形.

师：请用自己的话说一说，什么样的图形是轴对称图形？

生3：折叠后能重合的图形.

生4：沿着一条直线折叠后能完全重合的图形.

生5：还不准确，应该是沿着一条直线折叠后直线两旁的部分能完全重合的图形.

（师生完善轴对称概念：如果一个图形沿着一条直线对折，直线两旁的部分能够完全重合，这个图形就是轴对称图形）

师：轴对称图形研究的是几个图形？该图形沿直线折叠后直线两旁的部分怎样？

众生：一个图形；完全重合. （板书这两个关键词）

师：折痕所在的直线就是对称轴，注意对称轴是一条直线. 轴对称图形是一个具有特殊形状的几何图形.

点评：通过让学生自主剪一剪、议一议、折一折、想一想的过程，层层推进，使学生经历初步体验——深入探究——发现归纳这一知识形成的过程，帮助学生把握概念的本质特征.

精彩片段2：形成性练习阶段

图2是由五张全等的正方形组成的图案，只移动其中的一张能组成轴对称图形吗？

师：若用五张全等的正方形图片组成如图所示的图案，只移动一张能组成轴对称图形吗？同学们先独立思考，再同桌之间相互交流，看你能找到几种方法？（学生相互交流，气氛热烈）

师：哪位同学愿意把你的结果展示给同学们看？

（学生6上讲台用多媒体演示后老师追问为什么这样动就是轴对称图形，它的对称轴是哪条直线？）

（学生6演示了8种不同的方法，博得听课教师的阵阵掌声）

师：还有方法吗？哪位同学愿意演示一下你与刚才这位同学不同的方法？

（学生争相举手，学生7演示了四种不同的方法，还有很多同学要求上讲台演示）

师：由于时间的关系，老师就不找同学演示了，老师相信你们一定还有更多更好的方法，同学们课下继续探究，看一共有多少种方法.

点评：学生先独立思考后，再相互交流，最后利用多媒体让学生展示自己的探究成果，培养学生运用所学知识多角度、多方位解决问题的能力，使学生对知识的理解由感性认识上升到理性认识.

精彩片段3：深入探究阶段

师：我们再把目光转移到双喜图案中，若用一把剪刀沿双喜图案的对称轴剪开，并向两边移动相同的距离，（多媒体演示分双喜的过程）一个图形变成了两个图形，这两个图形也给人一种对称的美感，生活中有许多相似的图形，我们应该如何表述它们的关系呢？

（多媒体演示被分的两个单喜沿某条直线折叠重合的过程）

师：像这样把一个图形沿着某条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，互相重合的点叫对称点.

师：轴对称研究的是几个图形？

众生：两个.

师：这两个图形沿着某条直线折叠后怎样？

众生：完全重合.

师：轴对称研究的是两个图形，这两个图形完全重合. （板书：两个图形，完全重合）

师：成轴对称的两个图形全等吗？反过来，全等的两个图形一定成轴对称吗？

生7：成轴对称的两个图形全等，但全等的两个图形不一定成轴对称.

师：你能举一个反例吗？

生7：能，你看，用两块完全相同的三角板按不同的方式摆放.

师：这两块三角板能不能按某种方式摆放后成轴对称呢？

生7：可以.

师：由此可以发现轴对称图形研究的是两个全等的具有特殊位置关系的几何图形.

点评：学生画龙教师点睛，体现了教为主导、学为主体的和谐. 类比轴对称图形的探究过程研究两图形成轴对称的概念，借助把一个轴对称图形沿对称轴一分为“二”，两图形成轴对称，渗透轴对称图形与两图形成轴对称的联系. 这显示出执教者设计的高明.

精彩片段4：巩固练习阶段

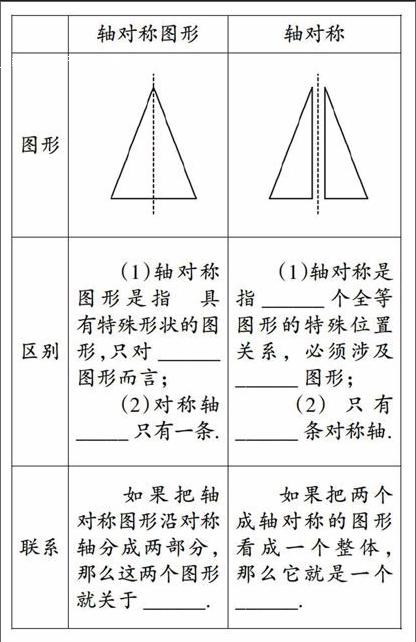
请同学们根据所示的轴对称图形和轴对称的相关知识完成下面的填空：

点评：轴对称图形与两个图形成轴对称的区别与联系是本节课的难点，从近两届省优质课发现，部分授课者都把两者人为地割裂开了，成为一个很大的遗憾. 门老师在这个问题上的高明之处是一方面在前面概念的得出过程中就有所渗透，另一方面采用填空的形式突破本节的难点，同时为了顺利完成这一问题，执教者还在前面练习题中通过问题“这两个国旗图案，若把它看成一个整体，它又是什么图形”来对第2小题有所暗示，透出执教者的良苦用心.endprint

精彩片段5：拓展提高阶段

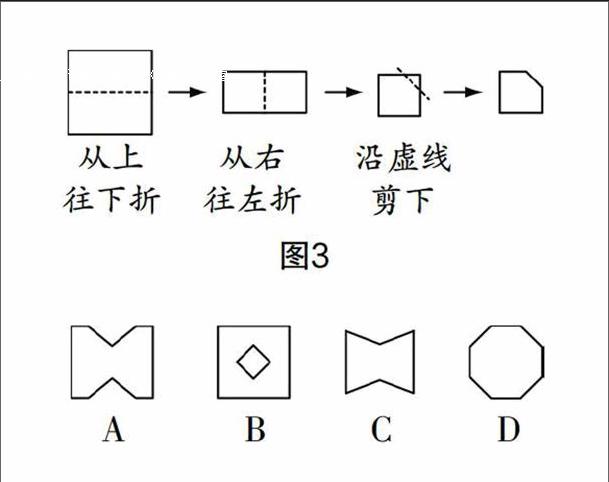
如图3，把一个正方形纸片按以下方向对折后，沿虚线剪下，再展开，则所得的图形大致是（ ？摇？摇 ）

师：先大胆猜一猜，是哪一个图形？

（学生有的说A，有的说B，还有的说C或D，并试图说服众人）

师：拿起你们手中的剪刀和纸，实际操作一下，看一看到底是哪一个图形？

（学生动手操作后确定是B）

师：为什么会是B这个图形呢？这里面有什么数学奥秘吗？咱们先看这样几个问题.

师：纸张对折的作用是什么？

众生：作轴对称.

师：对称轴在哪里？

众生：折痕所在的直线.

师：怎样用轴对称得到所求的图形？

生8：可以把剪过后的纸再打开看一看.

师：这个同学想得很好，这个图形在纸上不能打开，但能不能想一种方法达到这个目的呢？（老师用多媒体演示通过对称轴作轴对称的方法，得到B这个图形）

师：通过刚才的分析，我们知道可以从结果出发，先找出对称轴，通过对称轴向相反的方向作轴对称的方法确定展形后的图形？下面利用所得经验来看这个问题.

如果换个位置裁剪，如图4，展开后图形又是怎样的呢？

师：对称轴在哪？

众生：还是折痕所在的直线.

师：同学们用刚才的方法应该选哪一个图形？

生9：选D.

师：对于这个问题，若换个折叠方式呢？如图5，

众生：还是选D.

点评：利用轴对称构建几何图形，通过让学生观察-猜想-试验-思考-归纳，培养学生的空间想象能力，动手实践能力. 对课堂内容进行适当延伸，不仅加强本节课的趣味性，也让学生体验了数学在生活中的奇妙应用，同时也培养了学生在实际生活中“动眼-动手-动脑”的学习习惯.

课例赏析

本节课是一节较为成功的展示课例，灵动而扎实. 灵动体现在教师没有拘泥于教材，对教材进行了合理的重组与优化，使得整节课布局合理，节奏明快，浑然一体. 扎实体现在敢于给学生充分的时间，给学生时间去思考、去尝试，给学生时间去交流、去辨析，给学生时间去回味、去提升.

1. 设计灵巧，“双线”推近

本节课的设计大胆，没有采用通过欣赏图片，观察图片特征得出轴对称图形的一般方法，而是通过折叠双喜图后，直接给出轴对称图形的概念，在具体设计中有两条线索贯穿始终：（1）“玩”对称——“识”对称——“分”对称——“做”对称——“赏”对称；（2）感受美——分析美——欣赏美——创造美. 在第（1）条线索中主要通过双喜图这一民间剪纸艺术来展现，通过学生实际动手剪双喜图后，沿折痕折叠，折痕两边的部分完全重合，得出轴对称的概念，然后通过把一张双喜图沿对称轴剪开，并向两边平移相同的距离，这一分双喜图的过程，即得出了两个图形成轴对称的概念，也为学生找出轴对称图形与两个图形成轴对称的区别与联系做了铺垫. 在学生明确了两者的区别与联系后，通过“做”对称这一环节，使学生对二者的理解由感觉认识上升到理性认识，最后再通过欣赏对称图片，首尾呼应. 同时在整节课的设计中第（2）条线索——数学美贯穿始终. 本节课一开始通过欣赏《千手观音》视频，在数学上这是一种怎样的美？自然地引出本节课的内容，激发学生的求知欲和创造美的潜能，然后通过红火喜庆的双喜图案的剪、折、分等环节使学生一步步地去分析对称的美，接着通过欣赏图片，感受对称的美，最后在学生的作业中设计了学生创造美的环节. 在本课的结束也通过“数学给我们的不只是枯燥、乏味，也给我们带来无穷的美的享受，有人说，因为美，大自然选择了对称，可是同学们仔细地想一想，这其中难道只有美吗？”这样的内容，课虽尽，但意犹在.

2. 学生活动，贯穿始终

学生的学习离不开数学活动，数学活动的经验需要学生亲自参与数学活动过程，在实践中感知和领悟. 为使学生获得数学活动经验，本节课主要设计了如下的学生活动：一是通过学生的剪、折、分等活动，使学生通过自己的操作得出轴对称图形和两个图形成轴对称的概念，既避免了填鸭式的教学模式，又通过学生的操作理解了两个概念的区别与联系；二是在轴对称图形的概念得出以后设计了利用多媒体通过五张全等的正方形纸片，只移动其中一张构造轴对称图形的学生活动，使学生对轴对称图形的理解由感性认识上升到理性认识，在学生的实际操作中反响也很不错，学生的奇思妙想不时得到听课老师的阵阵掌声；三是通过逆向思维的方式，由一张正方形纸片经过两次折叠剪去部分后的图形，确定展开后图形的形状. 此环节的设置通过让学生观察——猜想——试验——思考——归纳，培养学生的空间想象能力，动手实践能力. 对课堂内容进行延伸，不仅加强本节课的趣味性，也让学生体验了数学在生活中的奇妙应用，同时也培养了学生在实际生活中“动眼——动手——动脑”的学习习惯.

3. 瞻前顾后，突显能力

一节成功的课不仅要完成本节的教学内容，还应重视前后内容的衔接，在本节课中轴对称图形及两个图形成轴对称的教学一方面利用上一章全等的内容去理解轴对称图形中对称轴左右两边的部分及成轴对称的两个图形，另一方面在判定一些几何图形是否是轴对称图形中有意安排了线段、角、等腰三角形等后几节要学习的几何图形，同时也设计了如平行四边形这种学生易判断出错的图形，既巩固了本节学习的内容，又为后面的教学做了铺垫.

当然教学永远是一门遗憾的艺术，如剪双喜的环节很多同学没有完成任务，这一环节如果先不让学生剪，直接通过学生折双喜图案，在本节课的最后让学生利用本节所学的轴对称图形知识想方设法剪一个双喜图案，会不会效果更好呢？

写在最后

蚌埠市教科所数学教研员陈耀忠对门老师这节课曾做如下评述：这节课一切看起来都很自然、流畅，给人以美的享受，在笔者听过的几十节“轴对称图形”课例中，本节课是唯一能够把轴对称图形与两图形成轴对称的关系是这样不露痕迹地、恰到好处地呈现出来的. 是呀，一节已被众多“大家”精彩演义的课，门老师却通过灵巧的教学设计，务实、高效地上出别样的风味，使老树绽放新花，这能否给我们的教学，提供某些启示呢？endprint