数学符号语言学习差异性分析及矫正策略研究

苟斌娥

引言

数学语言是数学文化传承的载体. 斯托利亚尔曾说：“数学教学就是数学语言的教学. ”学生学会了数学语言，就掌握了进行数学思维、数学表达和数学交流的工具. 符号语言作为数学语言的重要组成部分，实现了数学的简洁化和精确化，被认为是初中阶段最为核心的内容. 2007年颁布的《全日制义务教育数学课程标准（修改稿）》提出了“符号意识”和“数感”两个数学教育的关键词，并要求通过“数与代数”的学习，帮助学生构建符号意识. 符号意识主要是指“能够把数、数量的变化规律和关系运用数学符号进行表示；会用数学符号进行一般性运算、推理”. 符号意识的建立不仅能提高学生的数学表达能力，还可以通过符号意义的提取锻炼学生分析问题、解决问题的能力.

初中从算术到代数的转变过程中，数学符号的大量涌现成为初中生学习数学的主要障碍之一. 许多学生在学习数学符号时没有理解符号的真正含义，只是进行简单地机械记忆，导致符号学习与内在的知识经验脱节. 例如，学生常常因为不明白用符号语言叙述的题目条件而弄错题意；听课时因不能正确理解符号意义而无法理解课堂内容；解答问题的过程中由于不会运用数学符号而半途而废. 初中生，特别是刚跨入初中阶段的学生，不能正确运用符号语言把数学对象和数学问题准确地表示出来，使得他们的数学学习并不透彻、深入，进而无法为后继的数学学习打下基础. 因此，为培养学生的符号意识、提高学生获取符号意义的能力，寻找有效策略很有意义.

符号语言学习差异性分析

1. 符号语言的分类

根据不同的分类标准，许多学者对符号语言进行了相应的分类. 刘云章将数学符号分为元素符号、关系符号、运算符号、辅助符号四大类；曹校生在《初中数学符号语言分类教学与实验研究中》将符号语言分为“点”性符号、“线”性符号和“面”性符号三类；汤强从数学符号的不同用途将数学符号语言分为数量符号、运算符号、关系符号、结合符号和性质符号五大类；桂质亮提出了数学符号语言的三个层次：基本符号、组合符号、公式符号. 本文在已有研究的基础上，结合学生掌握数学符号语言的认知规律，将数学符号语言分为：概念符号（定义数学对象等）、运算符号（四则运算、关系运算等）、逻辑符号（命题间的等价转换、推出关系）、文本符号（文字语言描述、转化）四大类.

2. 差异性分析

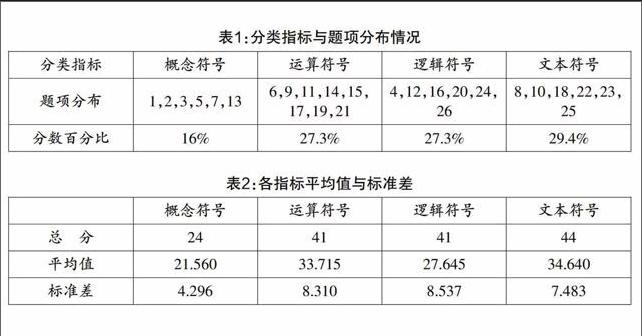
本文使用渝北区2013-2014学年度下期期末质量监测七年级数学试卷（总分150分），结合数学符号语言的分类，得出各指标与题项分布情况如表1所示.

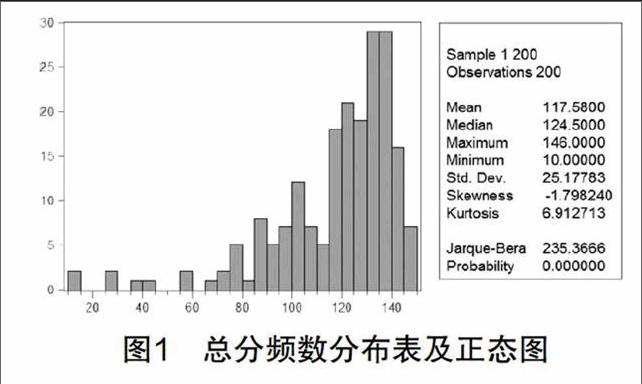
根据礼嘉中学初一学生200人完成试卷的情况，得到试卷总分的频数分布表和正态分布图（如图1所示），并统计出各个指标的平均分与标准差得到表2.

从图1可知，最高分为146分，最低分为10，平均分为117.58，说明大部分学生符号语言的掌握处于中等水平，还有很大的发展空间；标准差和极差较大，说明学生间存在显著的差异性. 通过进一步分析表明，学生之间在概念符号学习上不存在明显差异，而在逻辑符号、运算符号和文本符号的掌握上差异显著，即学生在理解符号语言的广度和深度上存在差异. 从表2可知，概念符号的得分率最高，且标准差较小，说明大部分学生已经基本掌握了基本概念并能进行简单地运用，但未理解概念的本质，所以不能灵活运用，导致其他符号语言学习上的困难；由逻辑符号的得分最低，表明学生在逻辑推理方面的学习上还存在一定的困难，因此在教学中更应加强学生的数理逻辑训练. 运算符号的标准差较大，且学生得分率不高，这与很多学生的学习习惯有关，大部分是由于马虎所致.

3. 差异性产生的原因

本文通过对测试结果进行分析，结合部分教师和学生的访谈，总结出数学符号语言学习过程中产生差异性的原因. 具体如下：

（1）教师对数学符号语言教学形式单一、内容比较凌乱. 根据王成营对初中数学符号的分类统计表可知，初一下学期学生要掌握的数学关键词为3个，数学概念为100个，数学符号为10个，数学图表为28个，数学公式和定理为17个，合计158个. 比小学阶段增加了近一倍. 因此，如果不进行系统教学，学生掌握起来会很吃力. 同时，由测验结果可以得出，教师在教学中忽视了概念本质的教学，不太重视教学过程，导致学生不能灵活地运用知识解题.

（2）学生没有养成良好的学习习惯. 这主要表现在书写不规范、表达不完整上. 这集中体现在计算题第19题和第21题上. 同时，在几何证明题第24题中，证明过程显得混乱，想到什么就写什么，缺乏逻辑性和严密性；公式、定理存在死记硬背、胡乱使用的情况. 如在几何证明题第20题中，将平行线的判定和性质颠倒使用；对符号语言的理解停留在表面，没有理解到本质. 又如选择题第1题，很多学生将分数误认为是无理数.

（3）学生的语言转化能力和逻辑推理能力较弱，不能完整地提取数学符号意义并进行各种语言间的等价转化和逻辑推理. 在应用题第25题的第（2）问中，四分之一的学生不能正确地将文字表达的题意转化为符号语言而导致求解错误；大约有95%的学生不能理解选择题第12题和填空题第18题的题意而不能正确求解；一半以上的学生证明第24题时思路混乱、缺乏逻辑性.

（4）部分学生缺乏学习兴趣和积极性. 某些学生觉得数学枯燥无味，加上基础知识掌握不牢固，使得其对数学符号语言的学习产生了厌恶心理，这是导致测验结果极差较大的主要原因.

教学矫正策略

根据以上差异性产生的原因，提出如下矫正策略：

（1）教师应进行系统地教学，从易到难、循序渐进. 可以将学生的数学符号语言能力培养分成符号识别、语言分析、意义建构三个阶段. 首先，从学生的读、写、算入手，培养学生的良好习惯，规范读写. 同时，增强学生的符号感，使学生不仅能区分性质符号与运算符号等，还能进行式的运算、方程与不等式的求解；其次，强化自然语言和数学语言之间的转换能力，使学生能将文字语言或图象语言转换成符号语言，能用方程或不等式解决实际问题，发展学生的符号意识；最后，培养学生提取数学符号意义的能力，使学生能够运用数学符号语言进行逻辑推理论证.

（2）教学中兼顾符号语言的“形式”和“内容”，形式是指符号语言的外部结构，内容是指符号语言所表达的意义. 形式外显、实质内隐，形式和内容犹如“形”和“神”，相互依存、不可分离. 因此，让学生从结构上、内涵上理解公式和定理，不仅可以牢记公式，而且有助于灵活运用，为有效地提取数学符号意义打下基础. 例如，进行绝对值教学时，3=3，-3=3，0=0，这时如果学生只根据形式就很容易得出-a=a.

（3）重视思维能力训练，培养学生的转化能力和逻辑推理能力. 让学生从符号语言的角度去认识、了解、解决生活中的实际问题，例如，利用方程和不等式解决实际问题时，要让学生学会将“不大于”“至多”“非负数”“超过”“互为相反数”等文字语言翻译为符号语言，进而运用数学知识和方法解决实际问题. 这有助于提高学生的数学语言表达能力，培养学生的数学建模思想.

（4）注重教学方式的多样性，培养学生的学习兴趣. 教学应与生活相联系，通过实际例子让数学教学变得丰富、生动，增进师生间的交流与合作，从而激发学生学习的积极性和主动性，使学生不会因为数学的抽象性而感到枯燥难学，从而失去兴趣.endprint