环形交叉口上游车头时距分布特征研究

徐锦辉，植叶妹，马丹辉，孔子浩，尹焕灶

（广州大学 土木工程学院，广东 广州510006）

环形交叉口是使进入交叉口的所有车辆都以同一方向绕岛行进的自行调节交叉口，避免了车辆交叉行驶。环形交叉口按中心岛直径大小分为常规环形交叉口、小型环形交叉口和微型环形交叉口三类。本文从道路交通流的车头时距特征入手分析环形交叉口上游的交通特性。对车头时距分布而言，可采用概率统计中的连续型分布描述，一般选用负指数分布、移位负指数分布、爱尔朗分布、威布尔分布、对数正态分布等，根据不同道路条件、交通条件和环境条件，国内外学者就车头时距分布采用或提出数学表达式复杂度不一的概率分布模型，并对模型进行描述，He等建立了移位负指数分布乘以高斯分布的综合概率分布模型。Mauro等从统计意义上阐释了移位对数正态分布，并结合实际交通问题验证了其实用性。韩萍提出了应用混合分布模型来描述环形交叉口复杂的交通流车头时距分布。陶鹏飞建立了能同时描述跟驰状态和自由流状态运行特征下的车头时距分布特性混合分布模型。在以往的研究中很少有对环形交叉口进口上游车头时距进行分析，本文拟结合环形交叉口实际路况进行车头时距分布研究。

首先对实地观测数据进行处理，整理出环形交叉口4个进口的4组车头时距数据；其次，本文选用负指数分布用以描述车头时距分布特征，并采用卡方检验对负指数分布做拟合优度检验，判断4组数据是否服从负指数分布；最后，通过车头时距分布拟合和拟合优度检验，确定环形交叉口适用于交通量不大的城市道路，其车头时距分布均服从负指数分布。

1 数据采集

为了对小型环形交叉口适用性进行分析，本文选取了广州金江大道—兴业大道路段环形交叉口进行实地观测，采集时间为2015年7月8日（周三），获取了该日上午7:50～11:50 4个进口车道上游连续4h的车头时距数据，观测断面距离斑马线上游30m处，观测点位的设定如图1所示。

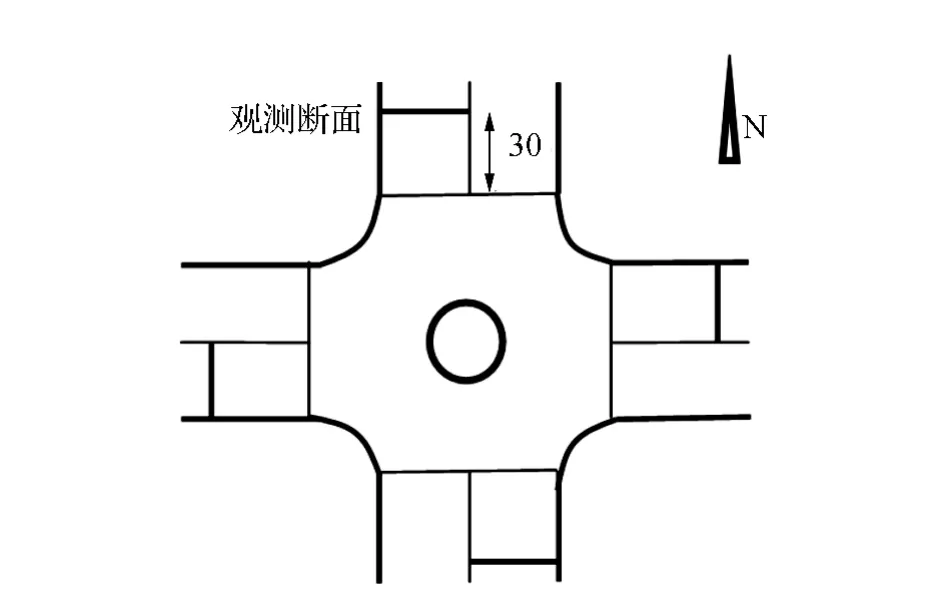
图1 环形交叉口车头时距观测点位示意图

按照图1所示的观测点位示意图，通过实地观测相应点位的车头时距，得到环形交叉口的交通调查基础数据，如表1所示。

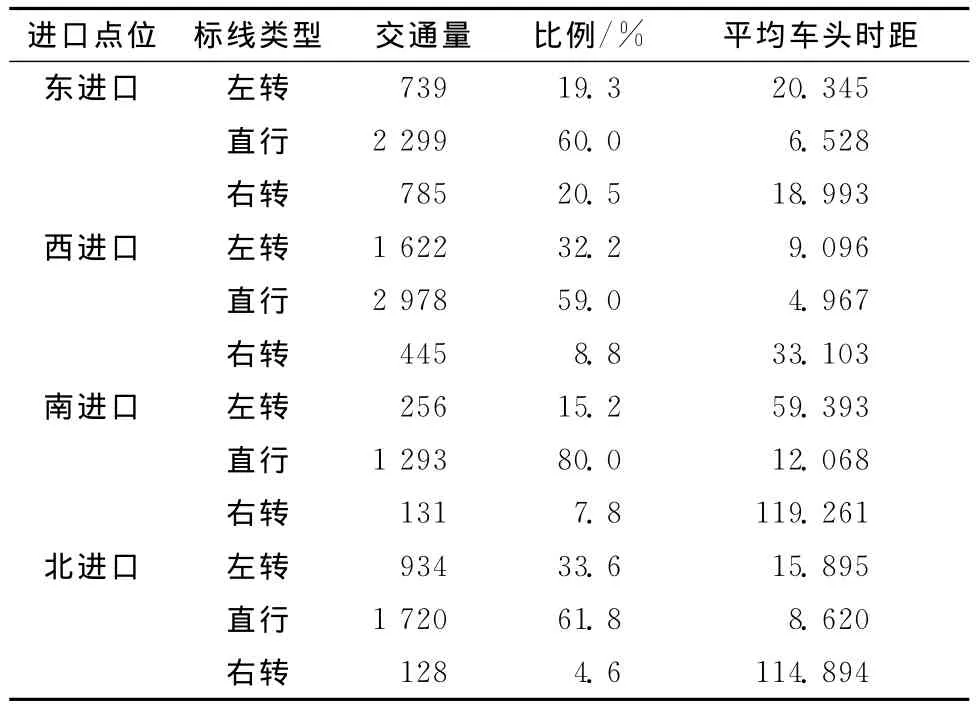
表1 环形交叉口的交通调查基础数据

根据表1可知，在3种标线类型中，直行车道的交通量占上游路段的总交通量比例最大，大于左转车道和右转车道的交通量，并且连续观测4h所获得的车头时距观测样本量最大，便于描述环形交叉口上游连续交通流的车头时距分布特征，本文采用获取到的4组直行车道的车头时距数据，描述环形交叉口上游的车头时距分布特征。

4个进口上游的直行车道车头时距统计分组数据，如表2～表5所示。

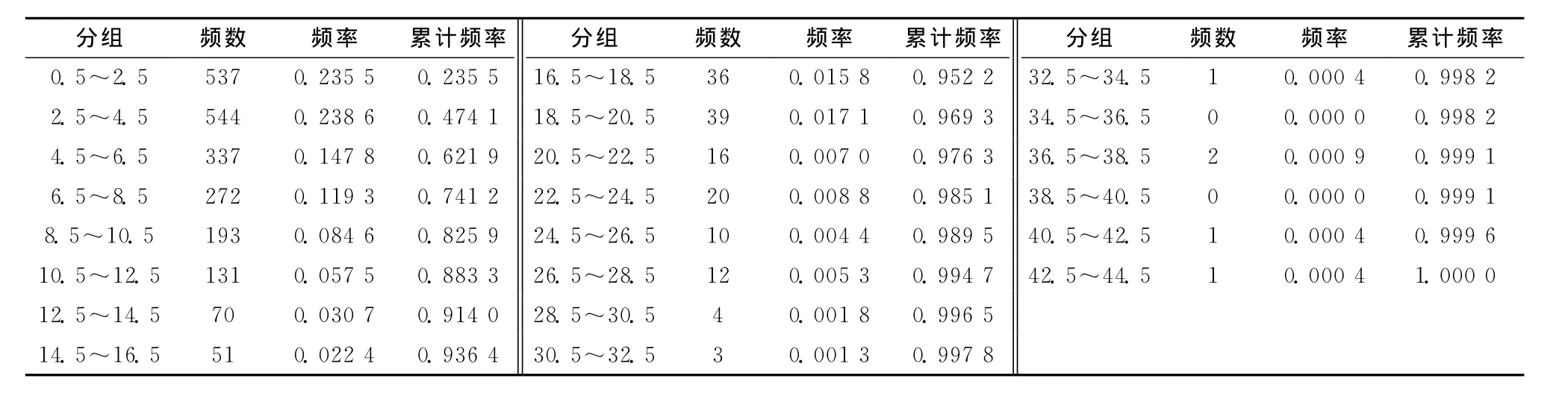
表2 东进口上游的直行车道车头时距

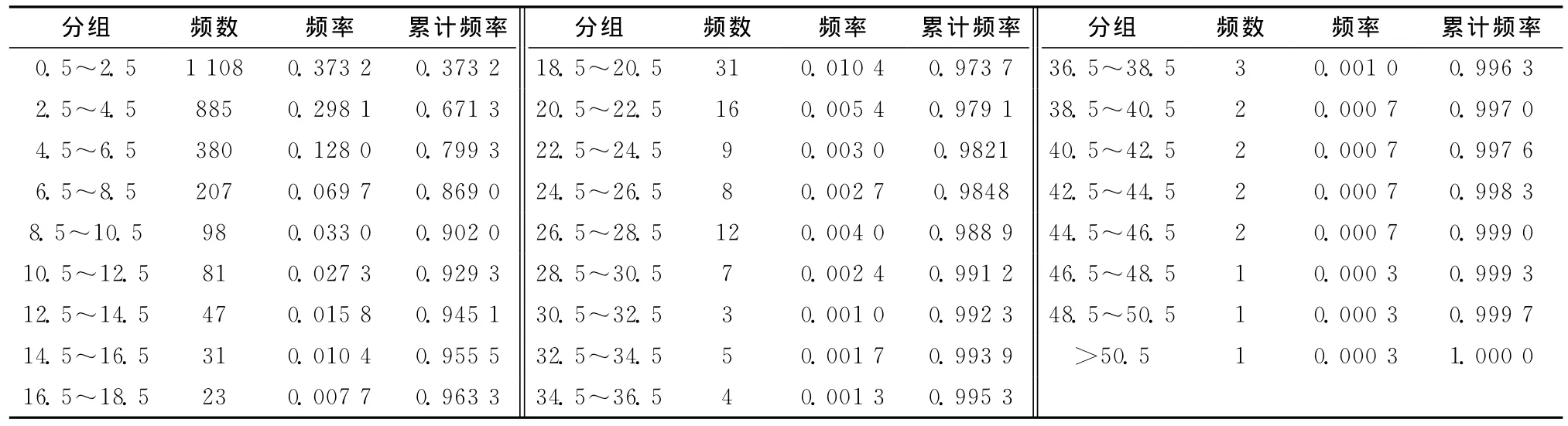
表3 西进口上游的直行车道车头时距

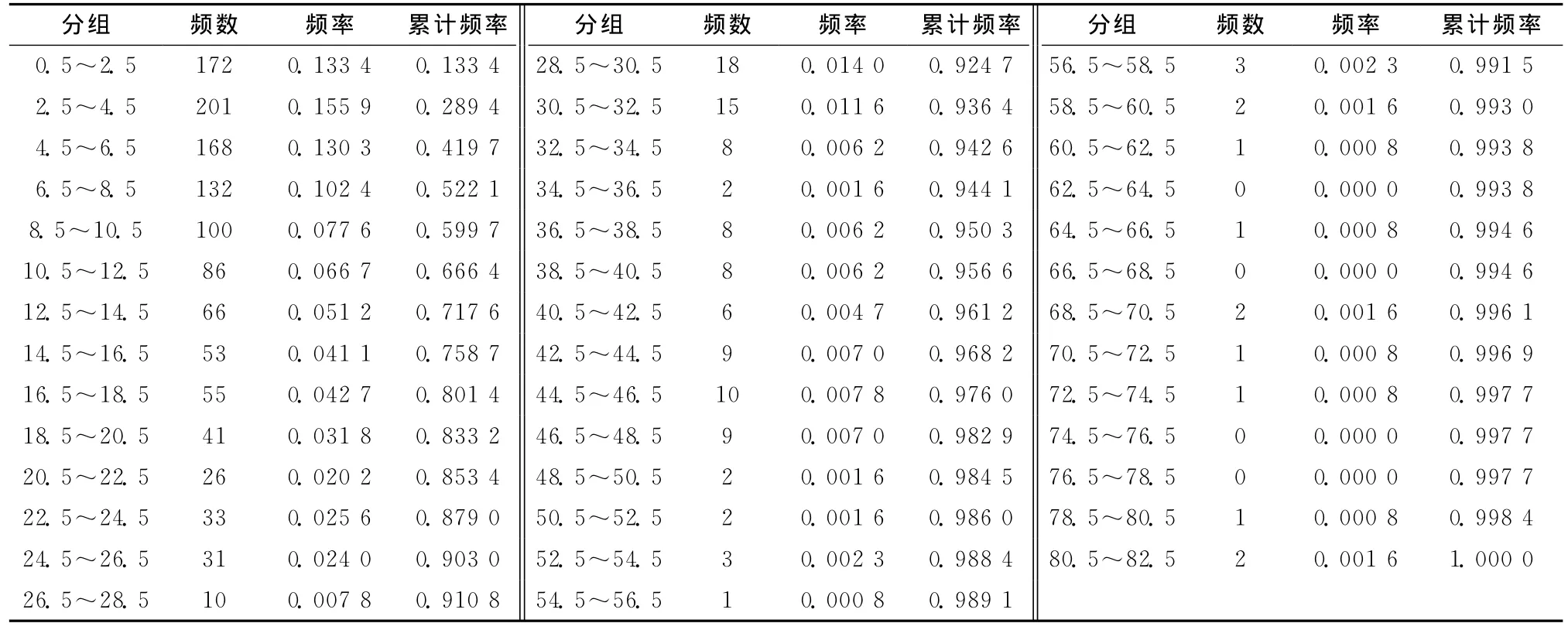
表4 南进口上游的直行车道车头时距

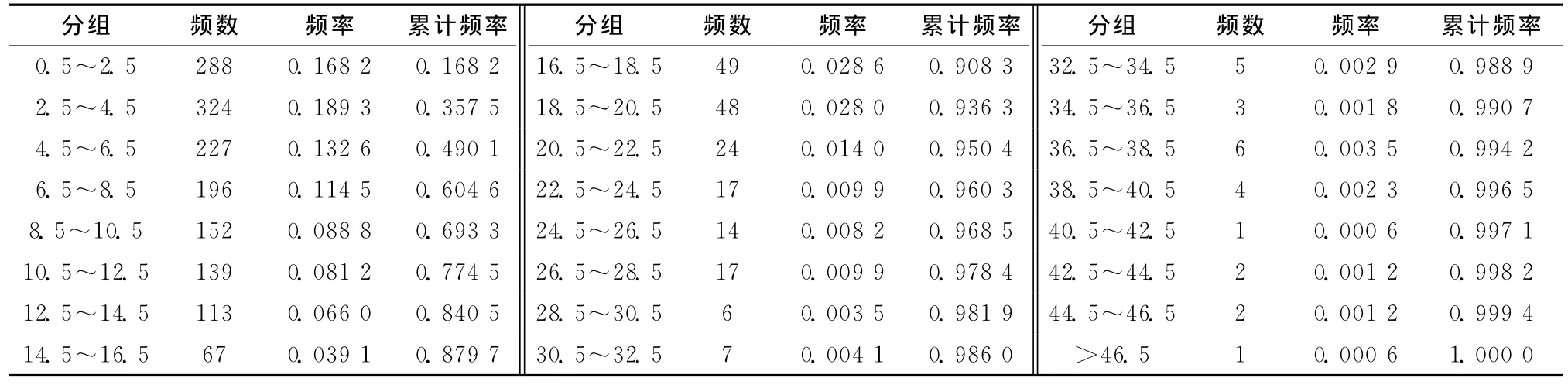
表5 北进口上游的直行车道车头时距

2 车头时距分布拟合

2.1 卡方检验

数理统计中通常将随机变量分为连续型随机变量与离散型随机变量，也存在独立于两者之外的随机变量，相应地，概率分布通常也分为连续型分布与离散型分布，在交通流理论中，通常将车辆到达视作离散型分布，常采用泊松分布描述车辆到达的随机过程，而作为随机事件发生时间间隔的车头时距则采用包括负指数分布在内的连续型分布进行描述。负指数分布广泛应用于描述车头时距分布，一般情况下适用于车流密度不大，车辆到达的随机性较大的情况。数理统计中，负指数分布的概率密度函数为

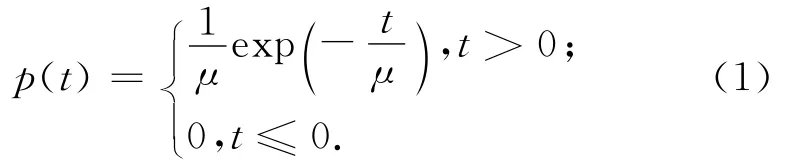
式中:μ为该随机变量的均值，在分析车头时距时，通常视作平均车头时距。

负指数分布的概率分布函数为

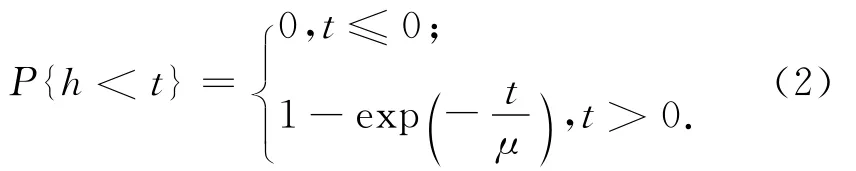
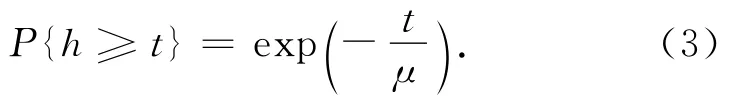
式中:h为车头时距值。

由此，本文采用P对车头时距数据进行拟合，并借助卡方检验进行拟合优度检验，设定显著性水平为5%，当卡方计算值大于卡方临界值χ2，则接收原假设。3个交叉口的车头时距分布拟合及卡方检验结果如表6所示。

根据表6，该观测的环形交叉口3个（东、南、北）进口上游的直行车道车头时距分布均接受负指数分布，即负指数分布可用于刻画3条道路进口交通条件下的车头时距分布。

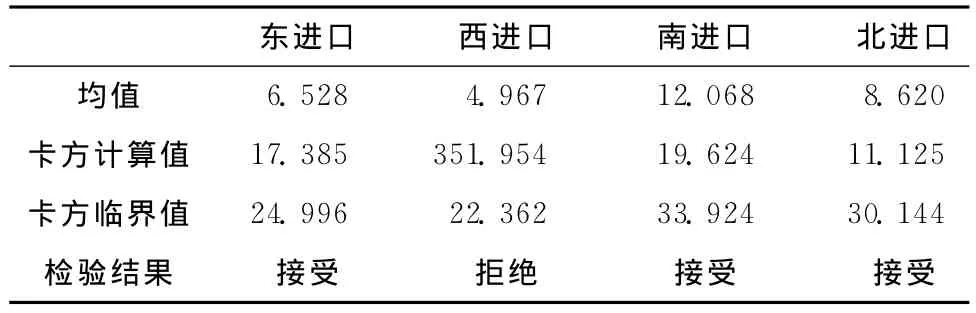
表6 车头时距分布拟合及卡方检验

2.2 分布曲线

根据表6中的负指数分布卡方检验结果，为较直观地描述车头时距分布情况，借助MATLAB分别绘制4个进口上游直行车道车头时距的分布，如图2～图5所示，其中，横坐标为车头时距值，纵坐标为P｛h≥t｝。

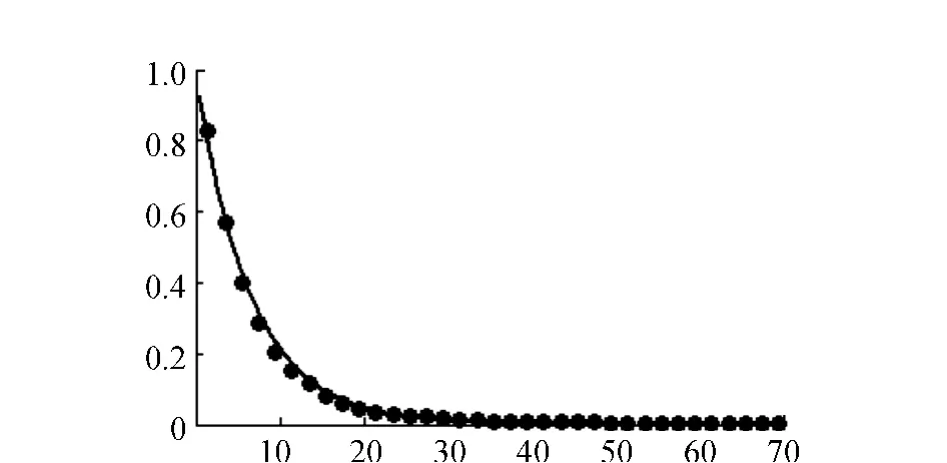
图2 东进口上游的车头时距分布

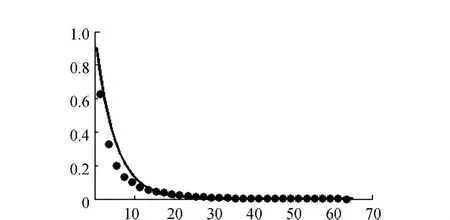
图3 西进口上游的车头时距分布

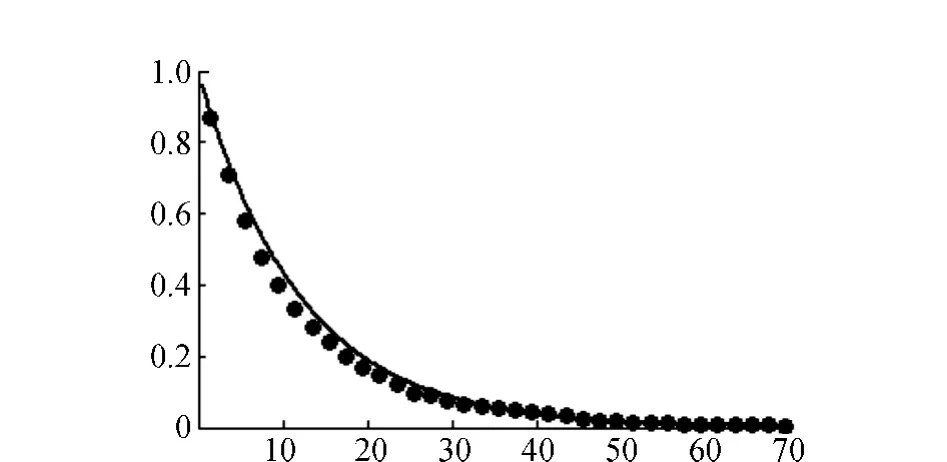
图4 南进口上游的车头时距分布

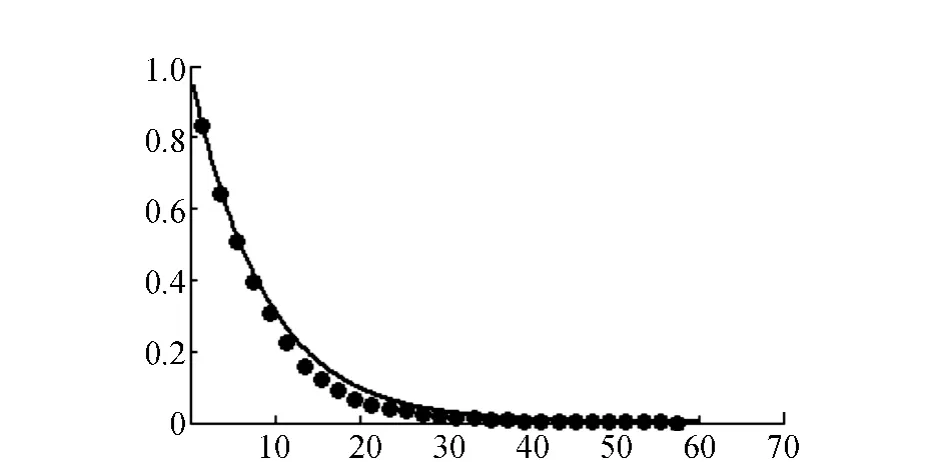
图5 北进口上游的车头时距分布

在4个进口上游车头时距分布拟合图中，东进口、南进口与北进口的拟合效果较好，均服从负指数分布；西进口拟合效果较差，不服从负指数分布。拟合效果图与卡方检验结果相对应。

3 结 论

本文采集了广州金江大道—兴业大道路段环形交叉口4个进口上游的车头时距数据，得到以下结论:

1）在连续观测的4个小时内每个进口道上游断面直行车辆最多，并且远大于左车道与右车道交通量，研究结果表明环形交叉口上游各车道的车头时距均具有泊松特性。

2）本文所采集的数据均来自交通量不大的主次路相交的次路路口，由于环形交叉口进口处采用让路控制，对采集的数据有一定影响，采集到的车头时距数据比自由流状态下的车头时距大。

3）通过选用负指数分布用以描述该道路条件下的车头时距统计分布特征，借助卡方检验对负指数分布做拟合优度检验，确定东、南、北进口车头时距数据均服从负指数分布，该结论可为适用于城市道路环形交叉口交通流的特性研究和交通管理提供参考。

4）本文的车头时距分布特征研究是从道路交通流的微观角度进行分析，负指数分布不仅可以用于描述环形交叉口上游车头时距分布，而且也说明了上游车辆的到达具有泊松特性，即车辆到达服从泊松分布，并且车辆到达规律与车头时距分布规律可用于模拟环形交叉口上游路段状况。

［1］ 王炜，过秀成.交通工程学［M］.南京:东南大学出版社，2011.

［2］ 李爱增，宋向红，马志博，等.信号交叉口下游车头时距分布特征［J］.交通运输系统工程与信息，2013，13（4）:66－75.

［3］ 郝晨羽，刘小勇.信号交叉口通行能力计算方法适用性研究［J］.交通科技与经济，2014，16（4）:22－25.

［4］ He Shu－yan，Guan Wei，Ma Ji－hui.Observed timeheadway distribution and its implication on traffic［C］∥Proceedings of the 12th International IEEE Conference on Intelligent Transportation Systems，St.Louis，USA，2009:803－808.

［5］ Mauro R，Branco F.Some proposed models as regards vehicular time headway［C］∥Transportation Research Board，Washington DC，USA，2010:2－4.

［6］ 韩萍.环形交叉口交通流运行特性［D］.长春:吉林大学，2011.

［7］ 陶鹏飞，王殿海，金盛.车头时距混合分布模型［J］.西南交通大学学报，2011，46（4）:633－638.

［8］ 任福田，刘小明，荣建.交通工程学［M］.北京:人民交通出版社，2008.

［9］ 邵春福，魏丽英，贾斌.交通流理论［M］.北京:电子工业出版社，2012:39－58.