气体稀薄效应对微机电系统(MEMS)气体轴承-转子系统不平衡响应的影响

杨琴,刘宇陆,张海军,祝长生

(1.上海大学应用数学与力学研究所, 200072, 上海;2.嘉兴学院数理与信息工程学院, 314001, 浙江嘉兴;3.嘉兴学院机电工程学院, 314001, 浙江嘉兴;4.浙江大学电气工程学院, 310027, 杭州)



气体稀薄效应对微机电系统(MEMS)气体轴承-转子系统不平衡响应的影响

杨琴1,2,刘宇陆1,张海军3,祝长生4

(1.上海大学应用数学与力学研究所, 200072, 上海;2.嘉兴学院数理与信息工程学院, 314001, 浙江嘉兴;3.嘉兴学院机电工程学院, 314001, 浙江嘉兴;4.浙江大学电气工程学院, 310027, 杭州)

为研究气体稀薄效应对微机电系统(MEMS)气体轴承-转子系统不平衡响应的影响,给出了MEMS气体轴承-转子系统运动方程和MEMS气体轴承的雷诺方程;利用双向隐式差分算法,给出了修正雷诺方程的详细数值求解过程;将转子运动方程与雷诺方程相结合,采用4阶龙格-库塔方法计算分析了气体稀薄效应对气体轴承-转子系统不平衡响应的影响。研究结果显示,考虑气体稀薄效应后,当质量偏心距较大时,MEMS气体轴承-转子系统的失稳轴颈转速较大,表明合适的偏心质量有助于改善系统的稳定性;在相同的质量偏心距下,考虑气体稀薄效应时气体轴承-转子系统在较低轴颈转速处出现峰值,表明此时不平衡偏心质量对气体轴承-转子系统运动的影响增大。

微机电系统;气体轴承-转子系统;不平衡响应;稀薄效应;双向隐式差分算法

作为新兴的研究领域,动力微机电系统(MEMS)具有体积小、重量轻、能量密度高的优点[1],近年来受到了国内外研究者的广泛关注[2]。基于MEMS加工工艺的动力MEMS由5层圆晶片装配而成,依靠外部压力气源驱动,其结构如图1所示。气体轴承-转子系统是动力MEMS的核心部件,因此对其进行动力特性的研究具有重要的应用前景。

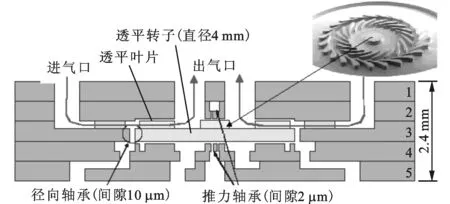
图1 动力MEMS的结构

美国的麻省理工学院集中了大量的人力和物力,针对微气体轴承-转子系统进行了理论和试验研究,分析了微气体轴承-转子系统的动力特性,但是在理论分析中没有考虑气体稀薄效应[3-6]。在稀薄气体动力学中,气体稀薄效应是指气流在壁面发生速度滑移、温度跃变和有效黏度变化等现象。本文主要考虑壁面速度滑移因素。基于一阶速度滑移边界,Lee等考虑了温度的影响,分析了微气体轴承的刚度和阻尼特性[7]。基于二阶速度滑移边界修正的雷诺方程,张文明等研究了微气体轴承-转子系统的稳态性能和稳定性,结果表明滑移边界可以提高MEMS轴承-转子系统的稳定性[8-9]。基于Fukui气体润滑模型,张小青等分析了微气体螺旋槽推力轴承-转子系统的非线性动力特性,结果表明考虑气体稀薄效应能够提高微轴承-转子系统的稳定性[10-12],这与张文明等得出的结论是一致的。针对一阶滑移边界修正的雷诺方程,张海军等采用有限差分法求解,分析了微气体轴承-转子系统动力特性的气体稀薄效应,表明气体稀薄效应对转子系统动力特性有较大影响[13-14]。

尽管国内外对MEMS气体轴承-转子系统进行了较多研究,但微尺度下其不平衡响应的气体稀薄效应还未见报道。为此,本文首先给出了MEMS气体轴承-转子系统的运动方程;然后针对MEMS气体轴承的雷诺方程,采用双向隐式差分算法,详细给出了其数值求解过程;随后将转子运动方程与雷诺方程相结合,采用龙格-库塔方法计算了MEMS气体轴承-转子系统的不平衡响应,分析了气体稀薄效应对其不平衡响应的影响。

1 MEMS气体轴承-转子系统运动方程

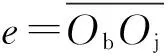
(1)

式中:fx、fy为轴承气膜承载力;fl为静态平衡时的外加载荷(包含转子自身的重量);em为转子质量偏心距;ω为转子角速度。为研究方便,假定φ=0°。

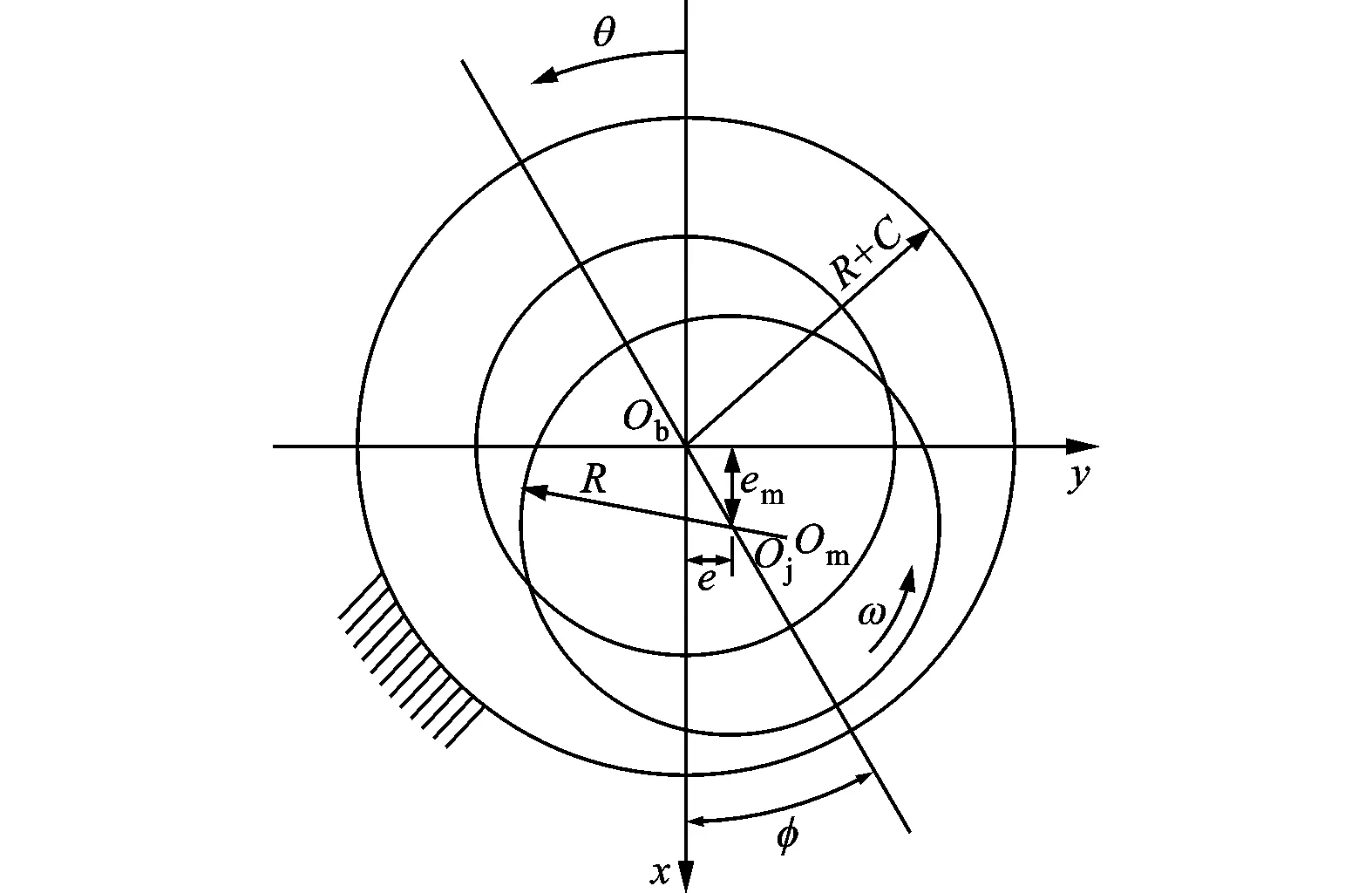
图2 MEMS气体轴承-转子系统结构示意图

(2)

其中R为轴颈(转子)半径,L为轴承的宽度,p为轴承气膜压力,pa为轴承外围气体压力。

2 MEMS气体轴承的雷诺方程

考虑气体稀薄效应,基于一阶速度滑移边界,归一化形式的微气体轴承雷诺方程[8,18-19]为

(3)

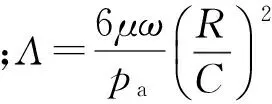
下面求解方程(3)的边界条件。

(2)对称性条件:轴承气膜压力关于轴向中间断面对称,即P(θ,ζ)=P(θ,-ζ)。

(3)周期性条件:轴承气膜压力是周期函数,即P(θ,ζ)=P(θ+2π,ζ)。

由于方程(3)是二维非线性偏微分方程,难以用解析方法求解,故通常采用数值方法求解,如有限单元法、有限差分法等。由于有限差分法原理简单,易于编程实现,应用较为广泛,所以这里采用交替双向隐式差分的方法求解。

令S=P2,方程(3)变为

(4)

式中

对时间相关导数项采用隐式差分格式离散

(5)

式中:S(n)表示时刻nτ的S,即S(nτ),假定为已求得的量;S(n+1)表示时刻nτ+τ的S,即S(nτ+τ),假定为待求的量。

将关于θ方向的二阶偏导数项作为未知量,而其他的偏导数项作为已知量,则式(4)变为

(6)

式中

对式(6)中的偏导数项采用中心差分格式离散,并简化整理,得

(7)

式中:i=1,2,…,N-1,其中N为θ方向的网格点数;j=1,2,…,M,其中M为ζ方向的网格点数;Ψ(n)作为已知量,有

令

则式(7)可写成

(8)

由于在θ方向S(n)具有周期性,因此在θ方向i从1到N-1式(8)都成立。将式(8)写成矩阵形式

(9)

式(9)为N-1维的线性代数方程组,其系数矩阵为周期三对角形式,可利用追赶法[20]求解。

最后,将关于ζ方向的二阶偏导数项作为未知量,而其他的偏导数项作为已知量,有

(10)

式中

类似地,对方程(10)中的偏导数项采用中心差分格式离散并化简,可得到M-2维的线性代数方程组,其系数矩阵为三对角形式,仍然采用追赶法求解。

这样经2次差分计算,可求得动态雷诺方程(3)的某一时刻的数值解,进而得到气体轴承的承载力,然后结合轴颈(转子)的运动方程(2),采用4阶龙格-库塔方法,计算出轴颈中心的轨迹和速度等数据,用来分析气体轴承-转子系统的不平衡响应特性。

3 转子系统不平衡响应分析

在进行转子系统不平衡响应分析之前,为了验证本文数值计算的有效性,选取美国麻省理工学院Piekos的计算结果[4]进行比较。计算中,选取转子不平衡质量偏心距为0.1 μm,得到转子运动轴心轨迹及其功率谱,如图3所示。从图3可以看出,两者的分析结果是相似的,均表明转子系统的运动为概周期运动形式,从而验证了本文数值计算的有效性。

选取气体轴承的参数如下:轴颈半径R=2 mm,轴承长度L=0.4 mm,径向平均间隙C=10 μm,偏心率ε=0.9,轴承外围压力为1.013×105Pa,气体动力黏度为1.8×10-5N·s/m2。为了更清楚地分析MEMS气体轴承-转子系统的不平衡响应,与不考虑气体稀薄效应(无速度滑移)的情形作对比。

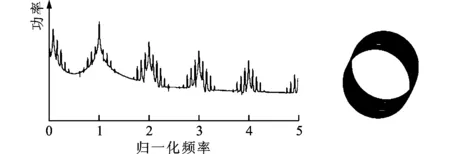
转子运动功率谱轴心轨迹(a)Piekos的数值计算结果[4]

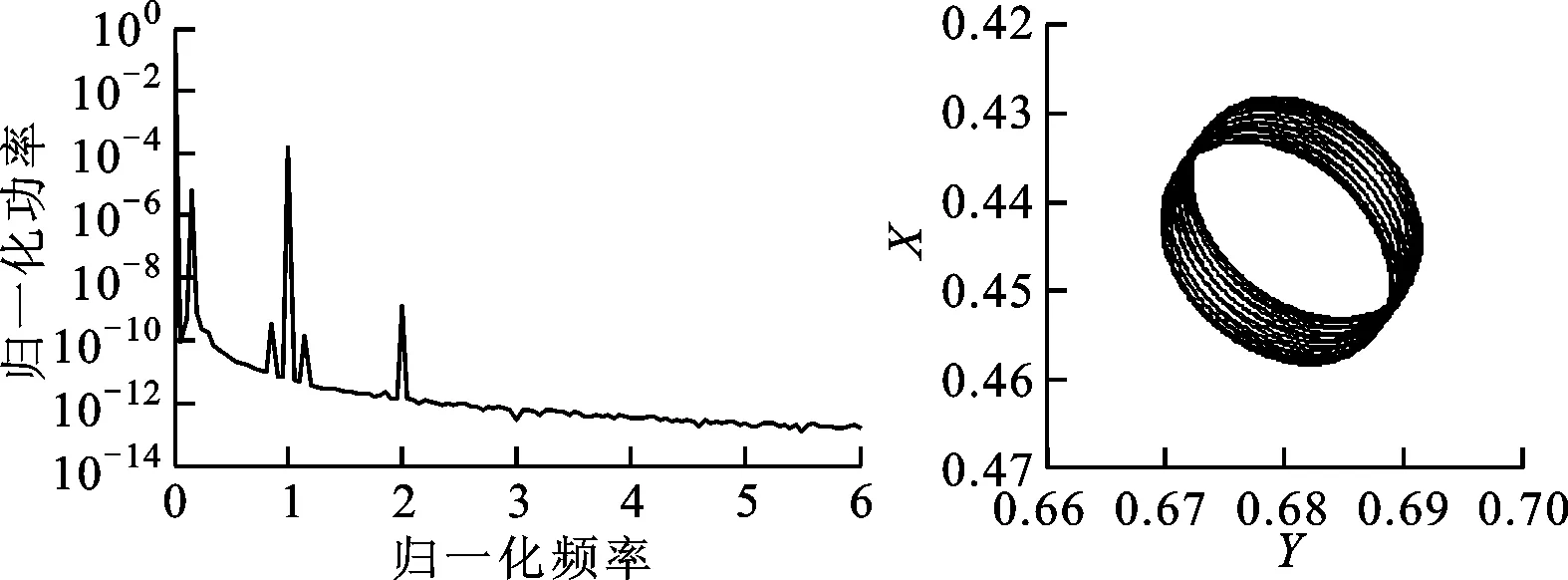
转子运动功率谱轴心轨迹(b)本文的数值计算结果图3 转子系统不平衡响应分析比较

取质量偏心距em为0.3、0.4、0.5和0.6μm,采用本文方法计算的MEMS气体轴承-转子系统的不平衡响应如图4所示。由图4可以看出:在不考虑气体稀薄效应的情况下,当质量偏心距较小时,随着质量偏心距的增大,转子系统的失稳转速增大;当质量偏心距为0.6μm时,转子的失稳转速降到了4×105r/min左右,表明合适的质量偏心有助于改善系统的稳定性,而过大的质量偏心会使系统在较低转速时就发生失稳;在考虑气体稀薄效应(速度滑移)的情况下,转子系统的不平衡响应变得复杂,表现为转速增加过程中出现了2个小的波峰,且波峰随质量偏心距的增大而增大。

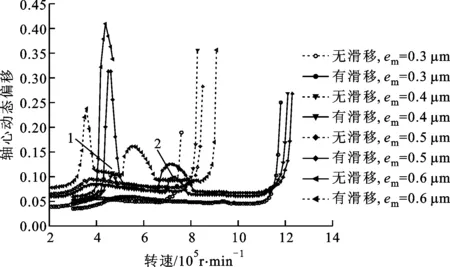
图4 MEMS气体轴承-转子系统的不平衡响应

下面针对质量偏心距em=0.4 μm的情况,进一步分析MEMS气体轴承-转子系统的非线性动态特性。

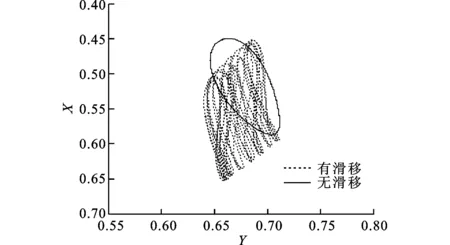
图5 波峰1处MEMS气体轴承-转子系统的轴心轨迹

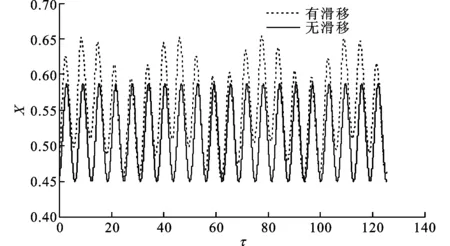
图6 波峰1处MEMS气体轴承-转子系统的时间历程

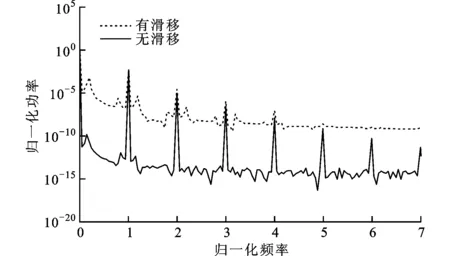
图7 波峰1处MEMS气体轴承-转子系统的功率谱

在图4所示的波峰1处,轴颈转速约为4.7×105r/min,MEMS气体轴承-转子系统的轴心轨迹、时间历程和功率谱分别如图5～图7所示。从图中可以看出:考虑气体稀薄效应(速度滑移)时,轴心轨迹表现为柱状涡动,功率谱除倍频成分外,在倍频附近仍有较大幅值的频率成分;不考虑气体稀薄效应(无速度滑移)时,轴心轨迹表现为稳定的涡动,功率谱主要表现为倍频成分。

在波峰2处,轴颈转速约为7.2×105r/min,MEMS气体轴承-转子系统的轴心轨迹、时间历程和功率谱如图8～图10所示。从图中可以看出:考虑气体稀薄效应(速度滑移)时,轴心轨迹表现为“内8字”涡动,功率谱除倍频成分外,在各倍频中间仍有较大幅值的频率成分;不考虑气体稀薄效应(无速度滑移)时,轴心轨迹表现为稳定的涡动,功率谱主要表现为倍频成分。

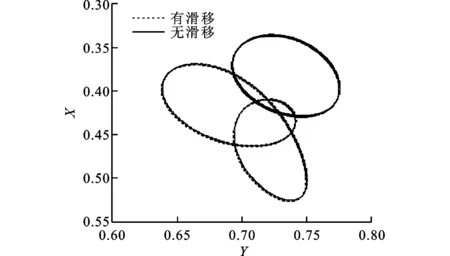
图8 波峰2处MEMS气体轴承-转子系统的轴心轨迹

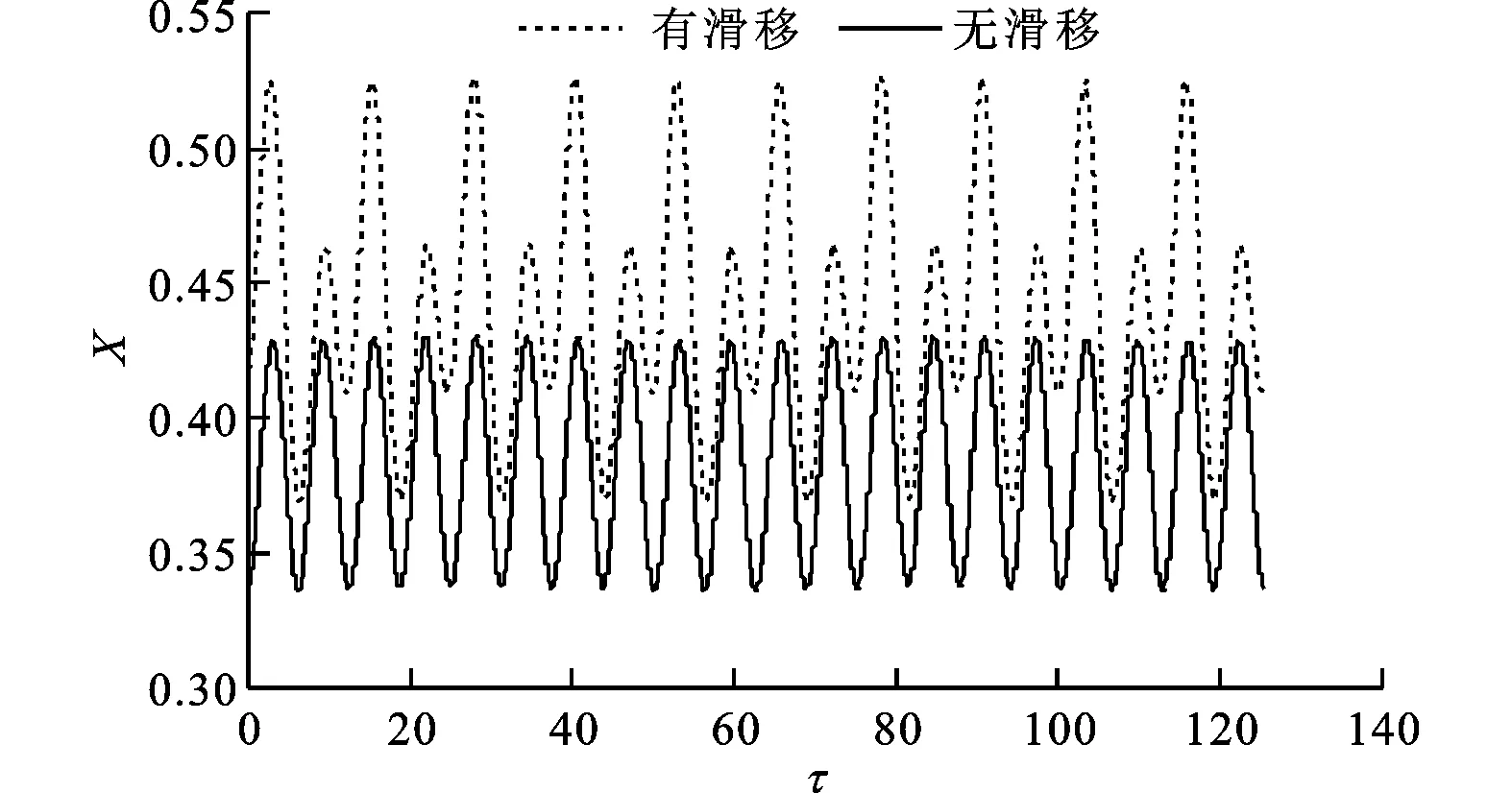
图9 波峰2处MEMS气体轴承-转子系统的时间历程

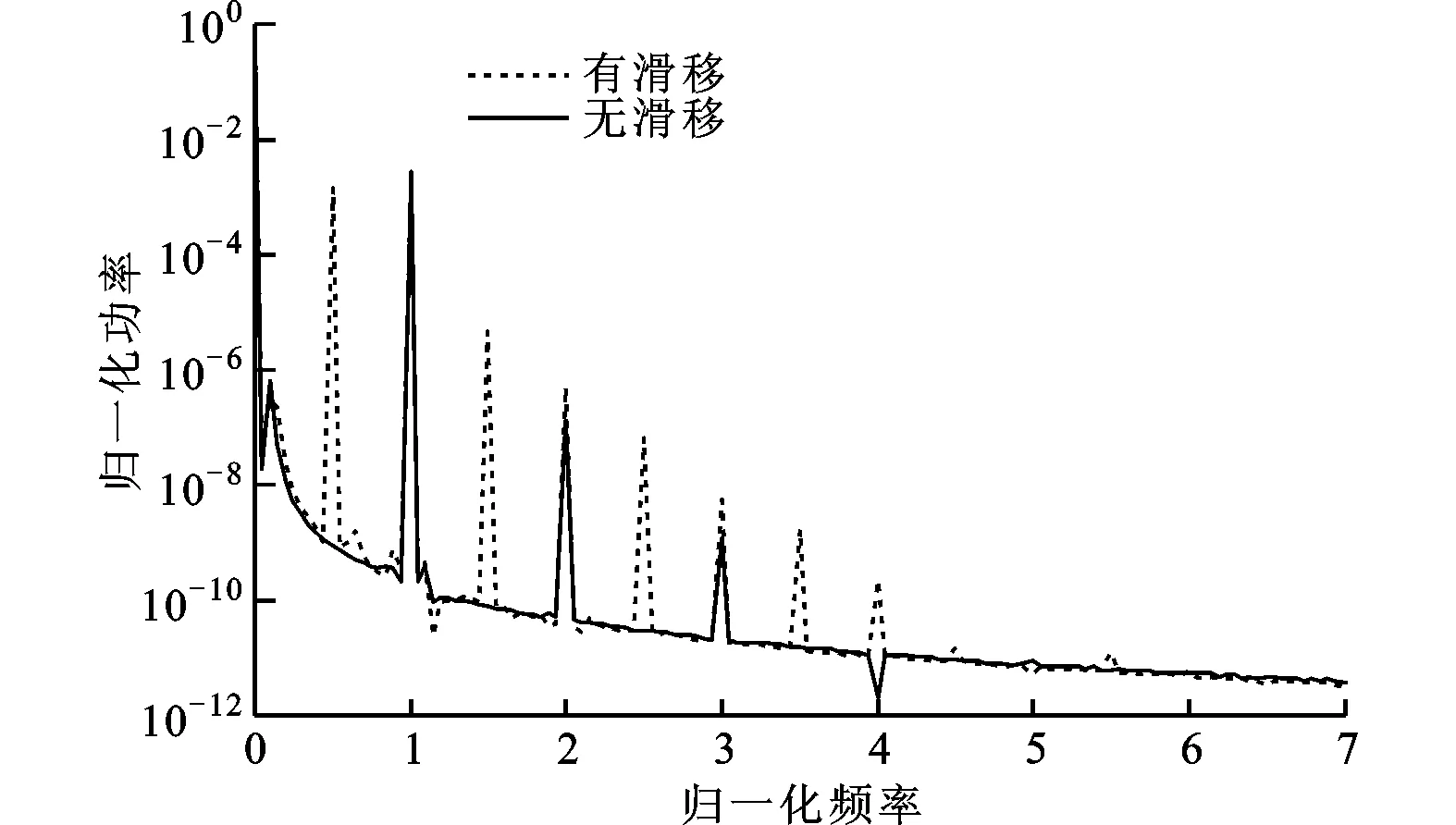
图10 波峰2处MEMS气体轴承-转子系统的功率谱

4 结 论

受气体稀薄效应的影响,MEMS气体轴承-转子系统的动态特性表现出不同的特征。本文采用双向隐式差分算法求解修正雷诺方程,结合转子运动方程,详细地分析了气体稀薄效应对MEMS气体轴承-转子系统不平衡响应的影响,结论如下:

(1)考虑气体稀薄效应(速度滑移)时,转子系统的失稳转速增大,表明系统的稳定性得到了提高,同时在质量偏心距较大的情况下,转子系统的失稳转速也较高,表明合适的质量偏心有助于改善系统的稳定性,这与相关文献的研究结论是一致的;

(2)在相同的质量偏心距下,考虑气体稀薄效应(速度滑移)时转子系统在较低转速处不平衡响应出现了峰值,表明此时不平衡偏心质量对转子系统运动的影响增大。

[1] EPSTEIN A H. Millimeter-scale, micro-electro-mechanical systems gas turbine engines [J]. ASME Journal of Engineering for Gas Turbines and Power, 2004, 126: 205-226.

[2] 孟光, 张文明. 微机电系统动力学 [M]. 北京: 科学出版社, 2008: 1-6.

[3] ORR D J. Macroscale investigation of high speed gas bearing for MEMS devices [D]. Cambridge, USA: Massachusetts Institute of Technology, 2000.

[4] PIEKOS E S. Numerical simulation of gas-lubricated journal bearings for microfabricated machines [D]. Cambridge, USA: Massachusetts Institute of Technology, 2000.

[5] TEO C J. MEMS turbomachinery rotor-dynamics: modeling, design and testing [D]. Cambridge, USA: Massachusetts Institute of Technology, 2006.

[6] LIU L X. Theory for hydrostatic gas journal bearings for micro-electro-mechanical systems [D]. Cambridge, USA: Massachusetts Institute of Technology, 2005.

[7] LEE Y, KWAK H, KIM C, et al. Numerical prediction of slip flow effect on gas-lubricated journal bearings for MEMS/MST-based micro-rotating machinery [J]. Tribology International, 2005, 38: 89-96.

[8] ZHANG Wenming, ZHOU Jianbin, MENG Guang. Performance and stability analysis of gas-lubricated journal bearings in MEMS [J]. Tribology International, 2011, 44: 887-897.

[9] 黄海, 孟光, 赵三星. 二阶滑移边界对微型气浮轴承稳态性能的影响 [J]. 力学学报, 2006, 38(5): 668-673. HUANG Hai, MENG Guang, ZHAO Sanxing. The effects of second-order slip-flow on the steady performance of micro gas bearing [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 668-673.

[10]ZHANG Xiaoqing, WANG Xiaoli, LIU Ren, et al. Influence of temperature on nonlinear dynamic characteristics of spiral-grooved gas-lubricated thrust bearing-rotor systems for microengine [J]. Tribology International, 2013, 61: 138-143.

[11]ZHANG Xiaoqing, WANG Xiaoli, ZHANG Yuyan. Non-linear dynamic analysis of the ultra-short micro gas journal bearing-rotor systems considering viscous friction effects [J]. Nonlinear Dynamics, 2013, 73: 751-765.

[12]刘韧, 王晓力. 微气体螺旋槽推力轴承润滑数值模拟 [J]. 机械工程学报, 2010, 46(21): 113-117. LIU Ren, WANG Xiaoli. Numerical predication of the performance of micro gas lubricated spiral groove thrust bearing [J]. Journal of Mechanical Engineering, 2010, 46(21): 113-117.

[13]张海军, 祝长生, 杨琴. 基于稀薄效应的微气体径向轴承稳态性能 [J]. 力学学报, 2009, 41(6): 941-946. ZHANG Haijun, ZHU Changsheng, YANG Qin. Steady characteristics of micro gas journal bearings based on rarefaction effect [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(6): 941-946.

[14]ZHANG Haijun, ZHU Changsheng, TANG Ming. The effects of rarefaction on the characteristics of micro gas journal bearings [J]. Journal of Zhejiang University: Science, 2010, 10(5): 43-49.

[15]谢友柏, 汤玉娣. 具有非线性油膜力的滑动轴承-转子系统振动特性的研究 [J]. 西安交通大学学报, 1987, 21(6): 93-104. XIE Youbai, TANG Yudi. Influence of non-linearity of hydrodynamic oil film forces on vibration characteristics of a journal bearing-rotor system [J]. Journal of Xi’an Jiaotong University, 1987, 21(6): 93-104.

[16]袁小阳, 朱均. 不平衡转子-滑动轴承系统稳定性的非线性研究 [J]. 振动与冲击, 1996, 15(1): 71-76. YUAN Xiaoyang, ZHU Jun. Study on the non-linear stability of unbalanced rotor bearing systems [J]. Journal of Vibration and Shock, 1996, 15(1): 71-76.

[17]MENG Guang, ZHANG Wenming, HUANG Hai, et al. Micro-rotor dynamics for micro-electro-mechanical systems (MEMS) [J]. Chaos, Solitons and Fractals, 2009, 40: 538-562.

[18]BURGDORFER A. The influence of the molecular mean free path on the performance of hydrodynamic gas lubricated bearings [J]. Journal of Basic Engineering, 1959, 81(1): 94-100.

[19]WU L, BOGY D B. New first and second order slip models for the compressible Reynolds equations [J]. ASME Journal of Tribology, 2003, 125(3): 558-561.

[20]王兴波, 钟志华. 求解周期性三对角方程组的广义Thomas 算法 [J]. 计算力学学报, 2004, 21(1): 73-76. WANG Xingbo, ZHONG Zhihua. Generalized Thomas algorithm for solving cyclic tridiagonal equations [J]. Chinese Journal of Computational Mechanics, 2004, 21(1): 73-76.

(编辑 葛赵青)

Influence of Gas Rarefaction Effect on Unbalance Response of Micro-Electro-Mechanical (MEMS) Gas Bearing-Rotor System

YANG Qin1,2,LIU Yulu1,ZHANG Haijun3,ZHU Changsheng4

(1. Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2. College of Mathematics Physics and Information Engineering, Jiaxing University, Jiaxing, Zhejiang 314001, China;3. College of Mechanical-Electrical Engineering, Jiaxing University, Jiaxing, Zhejiang 314001, China;4. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

To investigate the influence of gas rarefaction effect on the unbalance response of micro-electro-mechanical system (MEMS) gas bearing-rotor system, the motion equation of the MEMS bearing-rotor system and the Reynolds equation of MEMS gas bearing are presented, and the process of solving the modified Reynolds equation using the alternating-direction implicit difference method is given. The motion equation of the rotor and the modified Reynolds equation are combined, and the influence of gas rarefaction effect on the unbalance response of MEMS gas bearing-rotor system is analyzed using the 4th-order Rounge-Kutta method. The study shows that the stability speed of the journal of MEMS rotor system is higher with larger mass eccentricity when the gas rarefaction effect is considered, therefore, a proper eccentric mass of the rotor could improve the stability of MEMS gas bearing-rotor system. With the same eccentric mass, the peak value of unbalance response of MEMS gas bearing-rotor system emerged at the lower rotational speed, which shows that the unbalanced eccentric mass would have much influence on the motion of MEMS rotor system when the gas rarefaction effect is taken into account.

micro-electro-mechanical system (MEMS); gas bearing-rotor system; unbalance response; rarefaction effect; alternating-direction implicit difference method

2014-10-27。

杨琴(1980—),女,博士生;张海军(通信作者),男,副教授。

国家自然科学基金资助项目(11102071);教育部高等学校博士学科点专项科研基金资助项目(20070335184)。

时间:2015-04-29

10.7652/xjtuxb201507022

TH117.2

A

0253-987X(2015)07-0134-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150429.1437.006.html