液力变矩器的叶片数神经网络模型

王安麟,孟庆华,曹岩,韩继斌

(1.同济大学机械与能源工程学院, 201804, 上海;2.山推工程机械股份有限公司, 272073, 山东济宁)



液力变矩器的叶片数神经网络模型

王安麟1,孟庆华1,曹岩1,韩继斌2

(1.同济大学机械与能源工程学院, 201804, 上海;2.山推工程机械股份有限公司, 272073, 山东济宁)

针对一元束流理论无法量化表达叶片数对液力变矩器性能影响的缺陷和基于三维流体解析的液力变矩器叶片数设计中大组合、大计算量等难题,提出液力变矩器的叶片数神经网络模型。在结合台架试验数据确认三维流体解析结果准确的基础上,利用正交试验法合理地安排试验,并以三维流体仿真结果作为反向传播网络的训练样本;为提高反向传播网络的设计效率及收敛精度,引入遗传算法来优化反向传播网络的初始权重,训练后的反向传播网络可以对非训练样本集合的液力变矩器性能实现准确预测。研究结果表明,叶片数神经网络模型是基于整机性能匹配的液力变矩器定制化设计的桥梁,对提升整机作业效率具有重要的工程应用价值。

液力变矩器;叶片数;反向传播网络;遗传算法

液力变矩器广泛应用于车辆和工程机械。由于液力传动具有其他传动形式所不能比拟的优越性,因此液力变矩器的应用越来越广泛。

目前,液力变矩器的性能计算多采用一元束流理论和三维流体解析。一元束流理论将液力变矩器内部复杂的三维黏性流动简化成一元束流运动,应用欧拉方程对液力变矩器性能进行求解。由于一元束流理论假设叶片无限薄、叶片数无限多,故叶片数对液力变矩器性能的影响难以定量表达[1]。三维流体仿真避免了一元束流理论中的诸多简化和假设,现有的仿真软件能够较准确地模拟液力变矩器内部流体的真实流动[2],可以解析不同叶片数的液力变矩器性能,但液力变矩器的叶片数设计属于大组合问题,且三维流体解析耗时长、计算量大,不同叶片数的液力变矩器性能难以全面表达,亦无法满足当今数字化设计的需求。

本文提出液力变矩器的叶片数神经网络模型,以量化表达不同叶片数的液力变矩器性能,同时引入遗传算法对反向传播(back propagation,BP)网络的初始权重(权值和阈值)进行优化,以提高网络的设计效率和收敛精度,并结合整机系统的数字化模型来说明叶片数神经网络模型对当今液力变矩器定制化设计和提升整机作业效率的重要意义。

1 叶片数对液力变矩器性能的影响

液力变矩器为液力传动元件,而叶栅系统直接决定着液力变矩器的性能。叶栅系统参数主要包括叶片角、叶片厚度和叶片数等。除叶片角外,叶片数对液力变矩器性能影响亦较为显著。叶片数较多对提高能容量、减小液流出口偏离角和叶片上的负荷是有利的,但叶片数过多会使流道阻塞严重、相对速度提高、摩擦损失和冲击损失增大,且易出现气蚀现象。关于叶片数对液力变矩器性能的影响,范春顺通过三维流体解析分析得出,叶片数过多或过少都会造成液力变矩器性能下降[3];刘城等研究结果表明,泵轮和涡轮叶片数对最高效率和起动变矩比有较大影响,泵轮和导轮叶片数对泵轮扭矩系数有较大影响[4]。目前,叶片数的确定大多根据现有液力变矩器的尺寸、工作轮形式、叶片形状和厚度,或是运用经验公式确定,即

(1)

式中:R2为工作轮出口半径;l为叶片中间流线展开的轴面长度;c为经验系数,与工作轮形式、叶片形状和厚度有关。

根据上述经验公式确定的叶片数并不是最佳叶片数,通常还需要结合试验对比,以确定不同工作轮的实际最佳叶片数,但此过程开发周期长、成本高,已经不能满足当今的设计需求。总之,目前叶片数对液力变矩器性能的影响仍很难定量表达[1]。

液力变矩器性能不仅与其几何参数有关,还与泵轮和涡轮的转速有关。一元束流理论建立了液力变矩器性能与叶片角和泵轮、涡轮转速的函数关系,但无法建立液力变矩器性能与叶片数和泵轮、涡轮转速的函数关系,然而建立液力变矩器性能与叶片数和泵轮、涡轮转速的数学模型,对实现液力变矩器定制化设计和提升整机作业效率有着重要的意义。

2 基于三维流体解析的叶片数神经网络模型训练样本

神经网络的训练需要一定数量的训练样本,合理而准确的训练样本是其泛化能力的关键因素。训练样本不足会造成神经网络的泛化能力较差;训练样本过多且所有训练样本均通过物理试验获得,必然带来设计周期长、成本高等问题。随着计算机辅助设计(CAD)与流体动力学(CFD)软件的大量出现和软件功能的日益完善,为更好地设计结构复杂的液力变矩器、模拟液力变矩器内部流场的真实流动提供了更大的试验平台[5]。本文叶片数神经网络模型所需的训练样本通过CAD/CFD软件获得。

为检验CFD三维仿真结果的准确性,将台架试验数据与CFD三维仿真数据进行了对比,如图1所示。在不同传动比i下,变矩比K和泵轮扭矩系数λB的相对误差均小于3%,效率η的绝对误差小于5%,从而确认了三维流体解析结果的准确性。

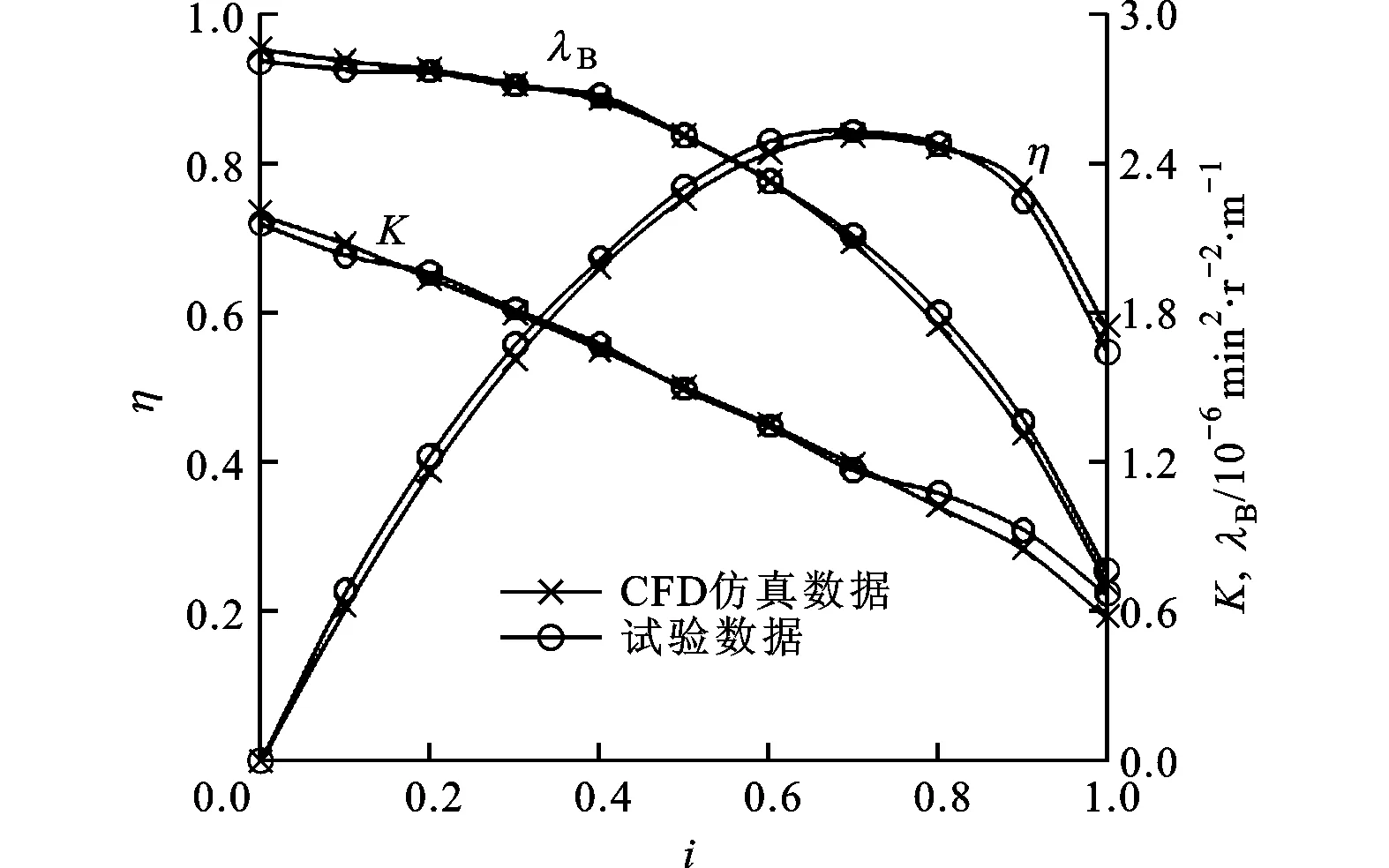
图1 CFD仿真与试验性能参数对比

液力变矩器轮系(泵轮、涡轮、导轮)的叶片数试验设计属于大组合问题,且CFD三维仿真对计算机内存要求高,计算耗时长,所以进行全面试验是不可行的。正交试验法[6]是应用一种由数码组成的排列均衡表(称为“正交表”)来安排试验以减少试验次数的科学方法,根据正交性从全面试验中挑选出部分具备均匀分散、齐整可比特点的试验代替全面试验,是一种高效、快速、经济的试验设计方法。本文液力变矩器轮系叶片数的试验设计包含了泵轮叶片数NB、涡轮叶片数NW、导轮叶片数ND这3个变量,每个变量分别取3个水平,如表1所示,因此选用的正交表为L9(34),并以9组试验代替全面试验。根据正交表在CAD软件中建立了9个液力变矩器三维模型作为训练样本模型。

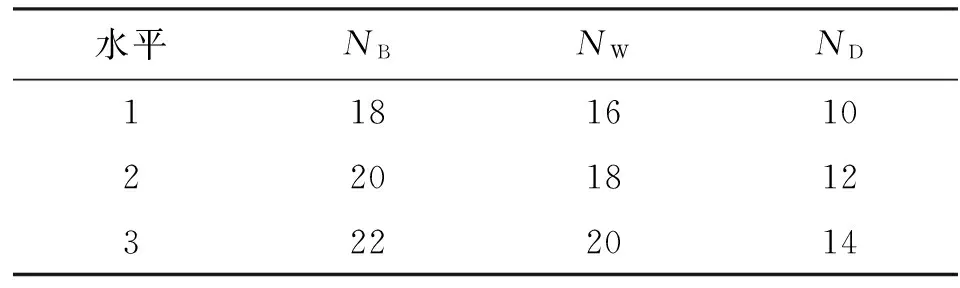
表1 液力变矩器叶片数变量的水平表

CFD三维仿真是把泵轮和涡轮转速作为输入,得到泵轮和涡轮的转矩,从而算得效率、变矩比等性能参数。本文的泵轮叶片数、涡轮叶片数和导轮叶片数取值范围分别为18～22、16～20、10～14,泵轮转速nB变化范围为1.6×103～2.2×103r·min-1,涡轮转速nW的变化范围为0～2.2×103r·min-1,这样叶片数神经网络模型对此范围内的各变量任意取值均可进行准确预测。由于叶片数和转速的变化范围相差较大,不能将叶片数和转速同时作为变量通过采用正交试验法安排试验。叶片数神经网路模型的5个输入变量中的3个叶片数变量采用正交试验法安排了9次试验,每次试验对应着一个训练样本模型,相应的泵轮转速从1.6×103～2.2×103r·min-1变化,在此转速变化范围内均匀地取40个点,而涡轮转速为泵轮转速乘i,i=0.0,0.1,0.2,…,0.9,1.0。叶片数神经网络模型的输入变量如表2所示。通过CFD三维仿真获得的泵轮转矩和涡轮转矩将作为目标变量。i为0.7时,仿真得到的泵轮转矩和涡轮转矩如图2所示,其为叶片数神经网络模型的部分目标变量数据。

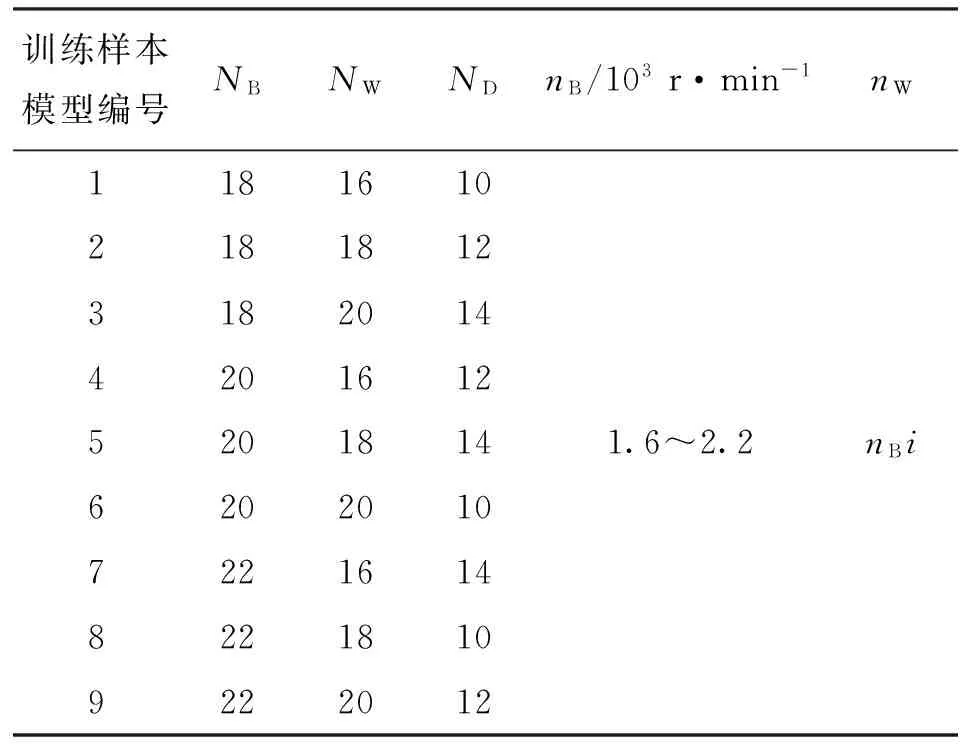
表2 叶片数神经网络模型的输入变量

由输入变量和目标变量即可确定神经网络所需的训练样本数据。

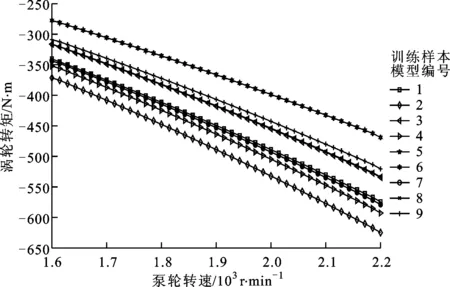
(a)泵轮转矩

(b)涡轮转矩图2 i为0.7时叶片数神经网络模型的 部分目标变量数据

3 叶片数神经网络模型

3.1 叶片数神经网络模型的结构

神经网络[7]是模拟生物神经网络进行信息处理的一种数学模型,目前神经网络已广泛应用于诸多领域[8-10]。BP网络是研究最多的网络形式之一,具有无限隐含层节点数的三层BP网络可以实现任意的从输入到输出的非线性映射。本文采用三层BP网络建立了液力变矩器的叶片数神经网络模型,如图3所示。

图3 叶片数神经网络模型

叶片数神经网络模型的建立,相当于建立液力变矩器性能与叶片数和泵轮、涡轮转速的函数关系,亦即

(2)

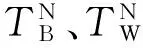
3.2 基于遗传算法的BP网络初始权重优化与训练

BP网络学习算法存在易于陷入局部极值点等缺陷,而且对初始权重较为敏感。为了防止出现网络陷入局部极值点而迭代提前终止的情况,通常需随机对初始网络的权重进行训练,再经过大量的仿真对比才可确定性能较好的网络。

遗传算法(genetic algorithm,GA)是一种高效的全局优化算法,可以并行地对网络初始权重进行优化[11]。引入遗传算法优化BP网络初始权重的流程如图4所示。

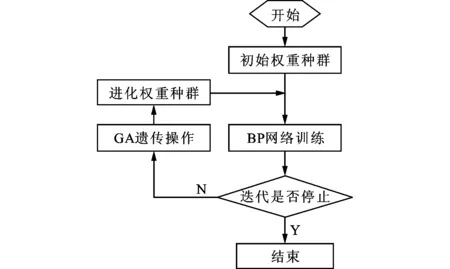
图4 遗传算法优化BP网络初始权重的流程图

由叶片数神经网络模型的结构可知,从输入层到隐含层的权值数为75,隐含层阈值数为15,从隐含层到输出层的权值数为30,输出层阈值数为2,权重总数为122。遗传算法采用了实数编码方式,因此染色体的基因数为122,适应度函数为网络预测误差,选择操作采用轮盘赌法,遗传算法的种群规模(种群数)为100,进化代数为50,交叉概率为0.8,变异概率为0.1。设置神经网络的训练次数为1×103,由此优化得到网络的最优初始权重。在该初始权重下,设置网络的训练误差目标值为1×10-4,对网络进行训练,训练误差曲线如图5所示。由图可知,迭代步数不到25网络即已收敛,且具有较高的收敛精度。

图5 训练误差曲线

3.3 叶片数神经网络模型的预测

为检验叶片数神经网络模型的泛化能力,选取表3中的泵轮叶片数、涡轮叶片数、导轮叶片数建立了2个测试样本模型,泵轮转速从1.6×103～2.2×103r·min-1变化,在此转速变化范围内均匀地取40个点,而涡轮转速为泵轮转速乘i,此处i为0.7,以说明网络的预测精度。

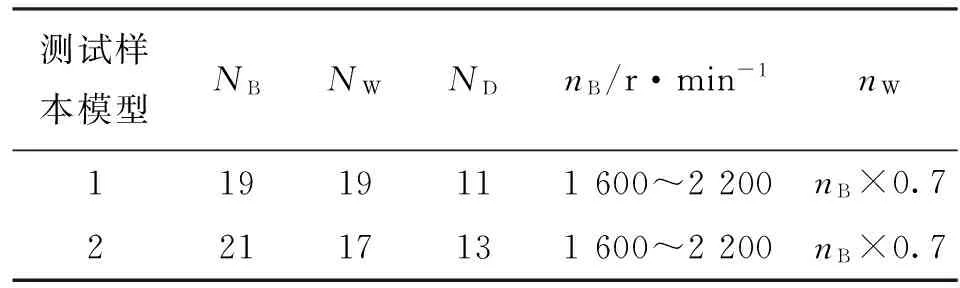
表3 测试样本输入变量

(a)泵轮转矩

采用叶片数神经网络模型对测试样本进行了预测,由此得到了泵轮转矩和涡轮转矩,并与CFD三维仿真结果进行了比较,如图6所示。由图可知,叶片数神经网络模型预测获得的转矩与CFD三维仿真结果的误差比较小。

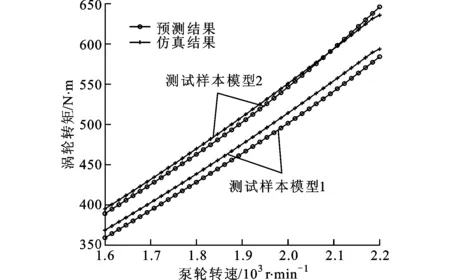
(b)涡轮转矩图6 预测与仿真转矩的比较

表4 神经网络预测的转矩平均相对误差及 最大相对误差

由表4可知,叶片数神经网络模型对转矩预测的相对误差均在3%以内,说明本文的叶片数神经网络模型对非训练样本集合的泵轮转矩和涡轮转矩做出了准确预测。

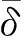
由表5可知,

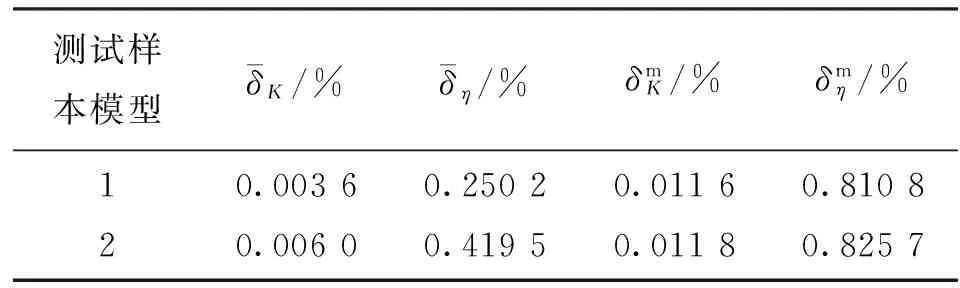
叶片数神经网络模型对变矩比的表5 神经网络预测的变矩比和效率的 平均误差和最大误差

预测误差均小于0.02,效率的预测误差均小于1%,进而说明本文的叶片数神经网络模型可以对非训练样本集合的液力变矩器性能实现准确预测。

试验表明:叶片数神经网络模型对本文范围内的各变量进行任意取值均可实现准确预测,预测的转矩相对误差均在5%以内,计算所得的变矩比误差均小于0.05,效率误差均小于3%。

4 基于整机性能匹配的叶片数神经网络模型

传统液力变矩器优化设计方法的目标是为了提高液力变矩器的性能,但整机作业效率不仅与液力变矩器的性能有关,还与整机的外部载荷、液力变矩器与发动机的匹配情况、整机的档位等有关,单纯提高液力变矩器的性能并不一定会提高整机的效率。

目前,整机与液力变矩器的配合普遍存在主配(主机与配件)分离问题,即液力变矩器的设计并不是针对某种特定的机型,而每种机型的常用工况和所受载荷差别很大,故迫切需要设计针对某种特定机型的液力变矩器,从而实现基于整机性能匹配的液力变矩器定制化设计,以提高整机的作业效率。液力变矩器的优化应以提高整机作业效率为目标,而不是单纯地提高液力变矩器的性能,需将液力变矩器与整机进行匹配来评价性能的好坏。如果通过试验对液力变矩器进行优化势必带来开发周期长、成本高等问题,因此可通过建立整机的数字化模型,以仿真代替整机试验。为保证整机数字化模型的准确性,可以通过整机试验对整机数字化模型进行标定。液力变矩器与整机数字化模型相结合,需要建立液力变矩器的数学模型。一元束流理论可以建立液力变矩器性能与叶片角的数学关系,但无法建立液力变矩器性能与叶片数的数学模型,因此无法在整机中优化液力变矩器的叶片数。本文建立的叶片数神经网络模型可以实现与整机数字化模型相结合,从而达到在整机中优化叶片数的目的。叶片数神经网络模型与整机的结合框图如图7所示。

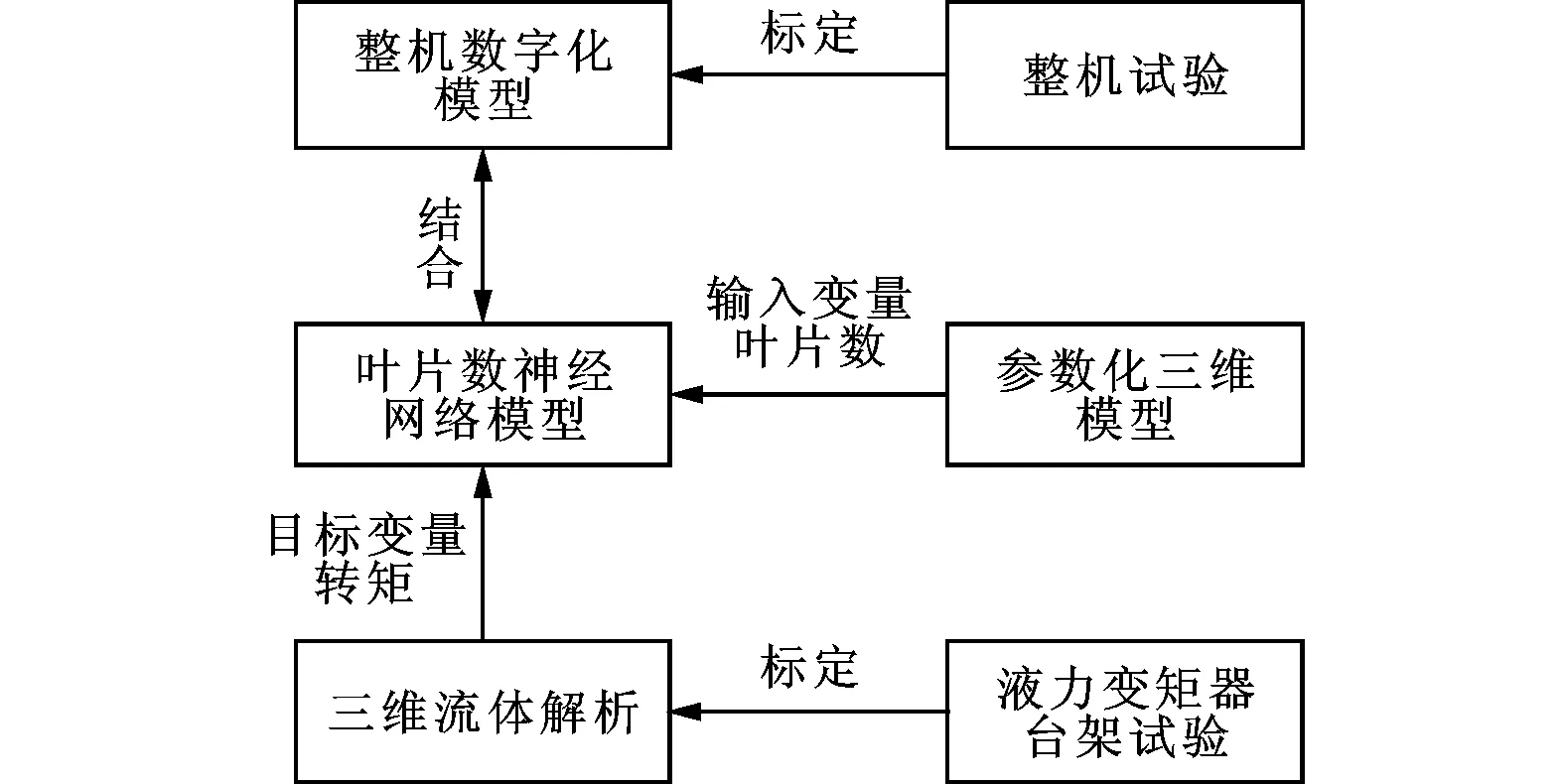
图7 主配结合框图

研究表明:在整机的数字化平台上实现了整机数字化模型与本文叶片数神经网络模型的结合,而且结合后的整机数字化模型仿真结果与整机试验结果相吻合,从而表明叶片数神经网络模型的可行性,适用于在整机中优化液力变矩器的叶片数。

5 结 论

(1)为解决目前无法量化表达叶片数对液力变矩器性能影响的难题,建立了液力变矩器的叶片数神经网络模型,利用正交试验法、通过合理安排试验解决了液力变矩器轮系中的叶片数试验设计的大组合问题,实现了叶片数神经网络模型准确预测非训练样本集合的液力变矩器的性能。

(2)为解决BP网络学习算法对初始权重较为敏感和目前初始权重的确定存在随机性问题,引入遗传算法对神经网络初始权重进行了优化,从而提高了网络的设计效率与收敛精度,缩短了网络的训练时间。

(3)通过与整机数字化模型相结合,阐明了叶片数神经网络模型应用于液力变矩器的数字化设计的可行性,实现了以整机作业效率提升为目标的液力变矩器叶片数优化,克服了传统主配分离设计中整机系统动力学设计空间与配件设计空间之间存在的设计变量耦合冲突的问题。叶片数神经网络模型是基于整机性能匹配的液力变矩器定制化设计的桥梁,对提升整机作业效率具有重要的工程应用价值。

[1] 朱经昌. 液力变矩器的设计与计算 [M]. 北京: 国防工业出版社, 1991: 120-126.

[2] JUNG J H, KANG S, HUR N. A numerical study of

a torque converter with various methods for the accuracy improvement of performance prediction [J]. Progress in Computational Fluid Dynamics, 2011, 11(3): 261-268.

[3] 范春顺. 液力变矩器叶片数对其性能影响的研究 [D]. 长春: 吉林大学, 2007.

[4] 刘城, 潘鑫, 闫清东, 等. 基于DOE及RSM的液力变矩器叶片数对性能的影响及优化 [J]. 北京理工大学学报, 2012, 32(7): 689-693. LIU Cheng, PAN Xin, YAN Qingdong, et al. Effect of blade number on performance of torque converter and its optimization based on DOE and response surface methodology [J]. Transactions of Beijing Institute of Technology, 2012, 32(7): 689-693.

[5] WU Guangqiang, YAN Peng. System for torque converter design and analysis based on CAD/CFD integrated platform [J]. Chinese Journal of Mechanical Engineering: English Edition, 2008, 21(4): 35-39.

[6] 田中玄一. 实验设计法概论 [M]. 北京: 兵器工业出版社, 1990: 9-12.

[7] 张德丰. MATLAB神经网络应用设计 [M]. 北京: 机械工业出版社, 2009: 1-9.

[8] EMBRECHTS M J, BENEDEK S. Hybrid identification of nuclear power plant transients with artificial neural networks [J]. Industrial Electronics, 2004, 51(3): 686-693.

[9] ABDOLLAHI F, TALEBI H A, PATEL R V. A stable neural network-based observer with application to flexible-joint manipulators [J]. Neural Networks, 2006, 17(1): 118-129.

[10]马晓丹, 刘刚, 周薇, 等. 基于量子遗传模糊神经网络的苹果果实识别 [J]. 农业机械学报, 2013, 44(12): 227-232. MA Xiaodan, LIU Gang, ZHOU Wei, et al. Apple recognition based on fuzzy neutral network and quantum genetic algorithm [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 227-232.

[11]MOMENI E, NAZIR R, ARMAGHANI D J, et al. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN [J]. Measurement, 2014, 57: 122-131.

(编辑 苗凌)

Blade Number Neural Networks Model of Hydraulic Torque Converter

WANG Anlin1,MENG Qinghua1,CAO Yan1,HAN Jibin2

(1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China;2. Shantui Construction Machinery Co., Ltd., Jining, Shandong 272073, China)

One-dimensional flow bundle theory is unable to quantitatively predict the influence of blade number on hydraulic torque converter performance. And there exist various combinations and huge calculations in blade number design based on 3D fluid analysis. Thus a blade number neural networks model of hydraulic torque converter was constructed. The accuracy of 3D fluid analysis results was confirmed in comparison with the bench test data, and simulations were arranged reasonably by orthogonal experiment method. 3D fluid simulation results were regarded as the training samples of back propagation (BP) neural networks. To improve design efficiency and convergence accuracy, genetic algorithm was introduced for optimizing initial weights and thresholds of BP neural networks, which achieved accurate predictions for non-training sample sets. The experiments show that blade number neural networks model serves as a bridge for hydraulic torque converter customization design based on vehicle performance matching.

hydraulic torque converter; blades number; back propagation neural networks; genetic algorithm

2014-11-19。

王安麟(1954—),男,教授,博士生导师。

重大科技成果转化项目资助(财建〔2012〕258号)。

时间:2015-04-27

10.7652/xjtuxb201507003

TH137

A

0253-987X(2015)07-0011-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150427.1754.001.html