任意曲线坐标系Euler方程S2流面的计算方法

李得英,宋彦萍,陈浮,郑振江,2,陈焕龙

(1.哈尔滨工业大学能源科学与工程学院, 150001, 哈尔滨;2.中国航天科工集团三十一研究所, 100074, 北京)



任意曲线坐标系Euler方程S2流面的计算方法

李得英1,宋彦萍1,陈浮1,郑振江1,2,陈焕龙1

(1.哈尔滨工业大学能源科学与工程学院, 150001, 哈尔滨;2.中国航天科工集团三十一研究所, 100074, 北京)

为提高S2流面计算方法对涡轮复杂几何的适应性和计算能力,详细推导了任意正交曲线坐标系下应用于流道中心S2流面计算的Euler方程,提出了任意曲线坐标系Euler方程S2流面的计算方法,发展了适用于三阶精度总变差减小的差分格式的数学模型,结合了隐格式时间推进、Riemann问题求解等技术。在应用于带弧形凸起的流道及某直叶栅气动参数计算,并对某三级低压涡轮进行性能预测的结果表明:所提方法对激波具有较高的捕捉精度,能够较准确地获得叶栅气动参数分布,且与实验结果吻合良好;对于多级涡轮总性能参数和气动参数分布均有较高的计算精度,是一种可为涡轮设计提供快速、可靠的计算方法。

S2流面计算方法;Euler方程;任意正交曲线坐标系;总变差减小的差分格式;低压涡轮

自吴仲华教授提出两类相对流面理论[1]以来,国内外学者发展了诸多S2流面方法,如流函数法、流线曲率法、欧拉法,并广泛应用于透平机械气动设计。其中,流函数法和流线曲率法具有求解简单、计算速度快等优点,但前者在跨音速流动求解中易出现密度双值问题[2],后者在求解通流参数时多基于轴对称假设[3-4],二者均无法准确捕捉叶片三维几何形线对流动参数的影响[5]。

在Euler方程求解S2流面定常流动参数的方法中,伪时间项的引入保证了控制方程为双曲型方程,且数值格式的发展使得求解稳定性和精度大为提高[6],但计算时间略有增加。S2流面方法快捷、准确,在工程实际中具有不可替代的作用。

Euler方程求解S2流面方法多采用圆柱坐标系下周向平均的Euler方程[7-8]。为提高对涡轮复杂几何的适应性和计算能力,本文推导了一种任意正交曲线坐标系下适用于S2流面方法的Euler方程,发展了求解流道中心S2流面流动参数的计算方法,并应用于某带弧形凸起的流道和某直叶栅气动参数计算及三级低压涡轮的性能预测。

1 Euler方程S2流面计算方法

本文采用图1所示的流道几何中心S2流面。相较于全三维方法,Euler方程S2流面方法可在合理计入叶片三维几何形状影响的前提下,大大减少计算资源,并保持较高的计算精度。

图1 流道中心S2流面示意图

1.1 控制方程

相对圆柱坐标系下且不考虑附加源项的守恒型Euler方程为

(1)

将其转换到任意正交曲线坐标系有

(2)

式中:

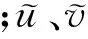
为避免繁琐的流面形状迭代修正,本文假设流道几何中心面为S2流面(见图1),且在贴体坐标系下ζ为固定值,即流面上任意点均满足

(3)

在任意正交曲线坐标系下存在如下关系式

(4)

根据式(2)、式(3)和式(4)可得S2流面控制方程

(5)

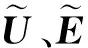
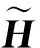
其中iz、ir和iθ为z、r和θ这3个方向的单位向量,根据式(3)易知F为静压作用于流面上的力。

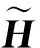
式(5)是任意正交曲线坐标系下的二维控制方程,其中的Jacobian矩阵行列式和变换系数与三维方程中表达有所不同。根据

xi代表ξ、η、ζ,i=1,3和式(4),可得适用式(5)的变换系数

Jξz=θζ(rη-r2φζrθη);Jξr=-θζ(zη-r2φζzθη);

Jξθ=r2φθζ(zηζr-rηζz);Jηz=-θζ(rξ-r2φζrθξ);

Jηr=θζ(zξ-r2φζzθξ);Jηθ=-r2φθζ(zξζr-rξζz);

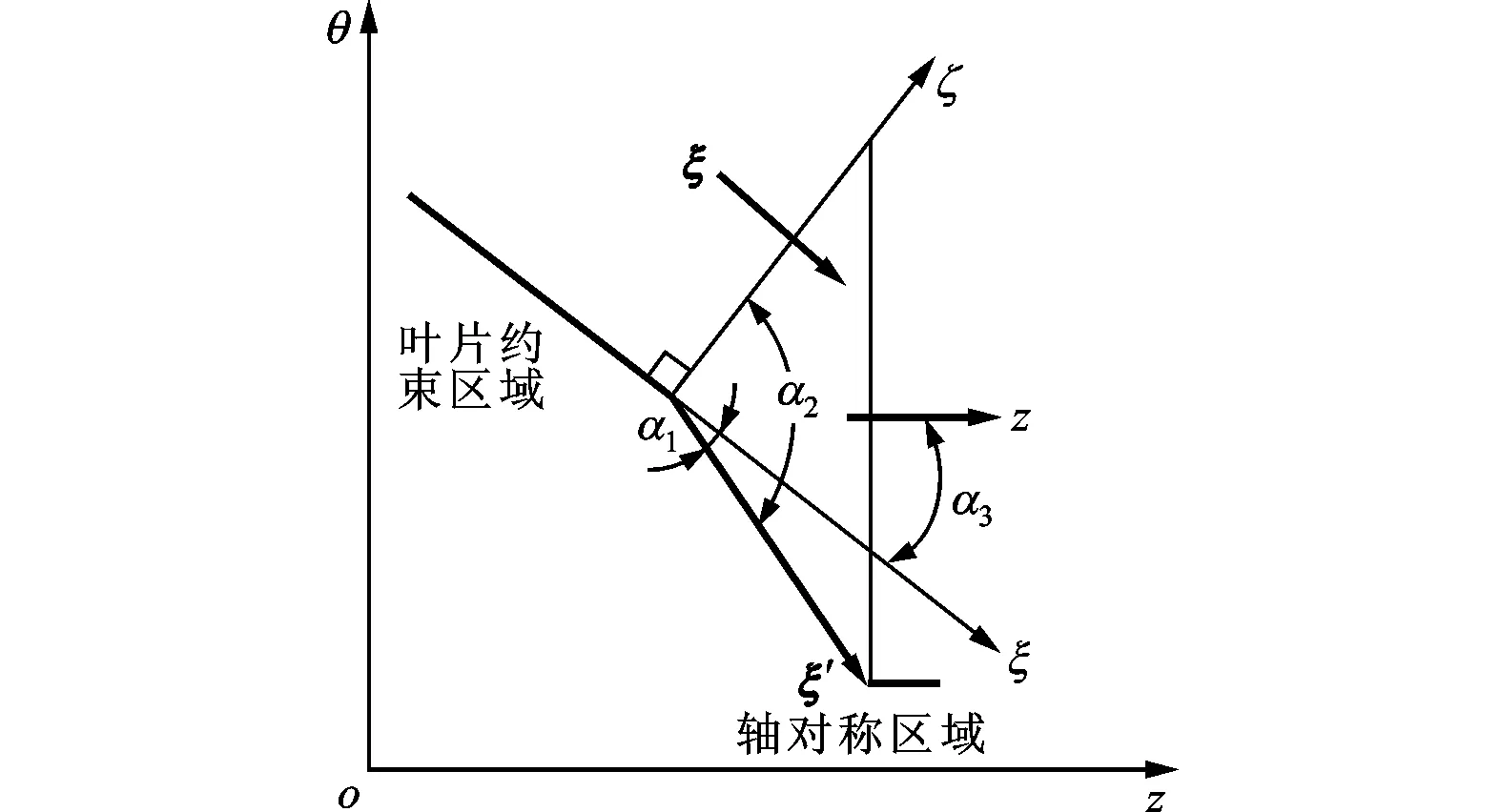
图2 尾缘处边界结构示意图

1.2 数值格式与方法

为避免交界面附近守恒型波模型产生压力波动[9],将式(5)中的守恒型变量转换为非守恒型变量进行离散求解,即

(6)

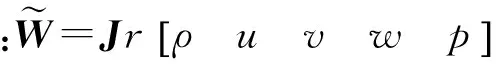
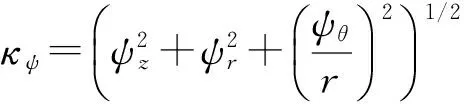
为加快求解速度,增加计算稳定性,采用隐格式时间推进和近似因子分解格式来求解式(6),即

(7)

利用迎风差分和总变差减小(TVD)的格式来求解式(7)左端微分项和右端通量项,可以增加计算稳定性,提高求解精度。本文应用了能够以高分辨率捕捉激波且无物理振荡的三阶精度Chakravarthy-Osher的TVD格式[10]。与Jacobian矩阵A和B相应的特征值矩阵Λ和左、右特征向量矩阵L、R的表达通式为

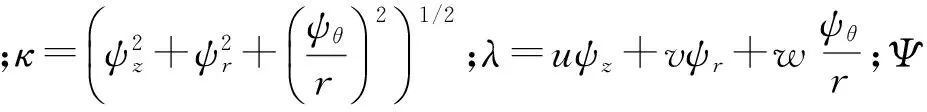
此外,应用Riemann问题精确解和近似解来处理交界面上参数数值传递不连续的问题[11]。

2 应用结果与分析

本文采用文献[12]模型进行了低压涡轮流动损失计算,利用文献[13]验证了本文数值格式的计算精度。

2.1 数值格式验证

图3是带弧形凸起流道的几何参数示意图。

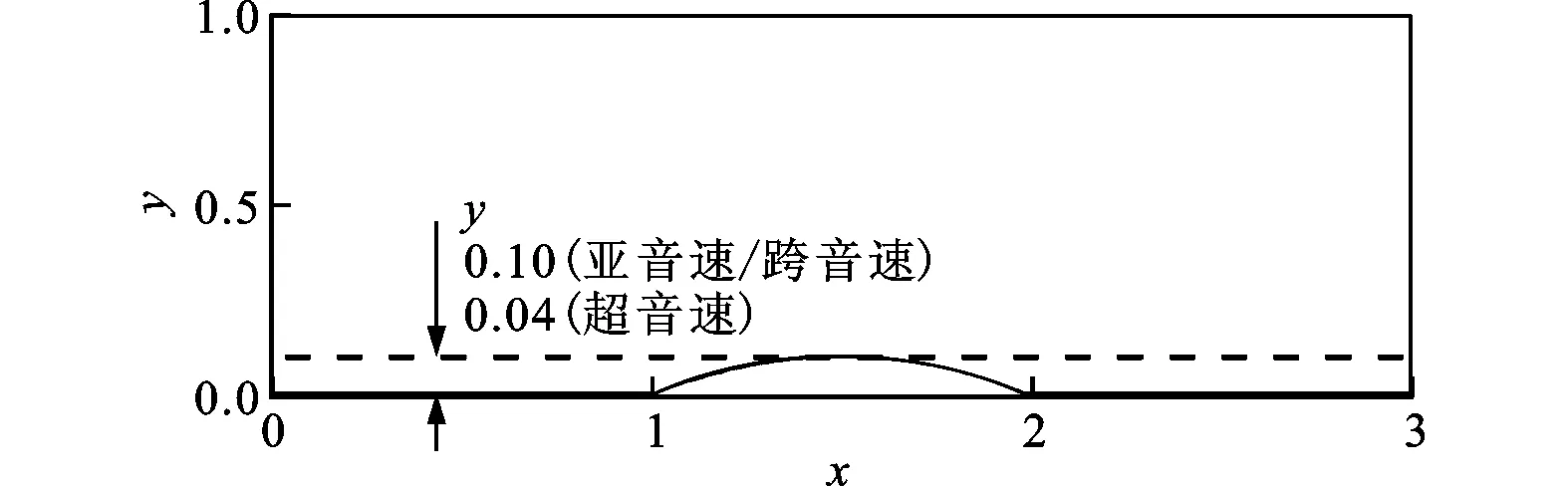
图3 带弧形凸起流道的几何参数示意

图4为亚音速、跨音速和超音速3种工况下计算所得的上、下端壁表面马赫数分布。从图中知:亚音速工况下计算所得马赫数具有较好的对称性,计算精度较高;较Karki结果,在跨音速流动中可准确地预测下端壁表面60%弦长处的激波,体现了本文TVD格式对流场间断的良好捕捉能力;在超音速流动中,下端壁凸起的前缘和后缘各产生了一道激波,前缘激波经上端壁反射后与后缘激波交叉,表明本文数值方法对马赫数等分布梯度较大的参数有较好的预测能力,数值格式计算精度也较为可靠。

2.2 直叶栅计算结果与分析

应用本文数值方法和Numeca方法(全三维计算)对某直叶栅气动参数进行了计算,并与实验结果进行了对比。图5为Numeca方法和S2流面方法的计算网格,其中Numeca方法计算网格数约49万,计算采用Navier-Stokes方程,选取Spalart-Allmaras湍流模型,壁面附近网格精度满足y+<5;S2流面方法计算网格轴向和径向计算节点数分别为61和31。计算时叶栅进口总压为107.05 kPa,入口总温为293 K,入口气流角为40.7°,出口背压为103.21 kPa。

图6为叶栅出口136%轴向弦长处上半叶高总压损失系数、马赫数及气流角径向分布。受栅内二次流动的影响,叶栅出口65%～88%叶高处存在显著的高损失区,采用二次函数表达二次流损失模型的S2流面方法能够较准确地捕捉该区域的高流动损失,主流区与端壁附近的流动损失与实验结果吻合良好,计算精度也比较高。

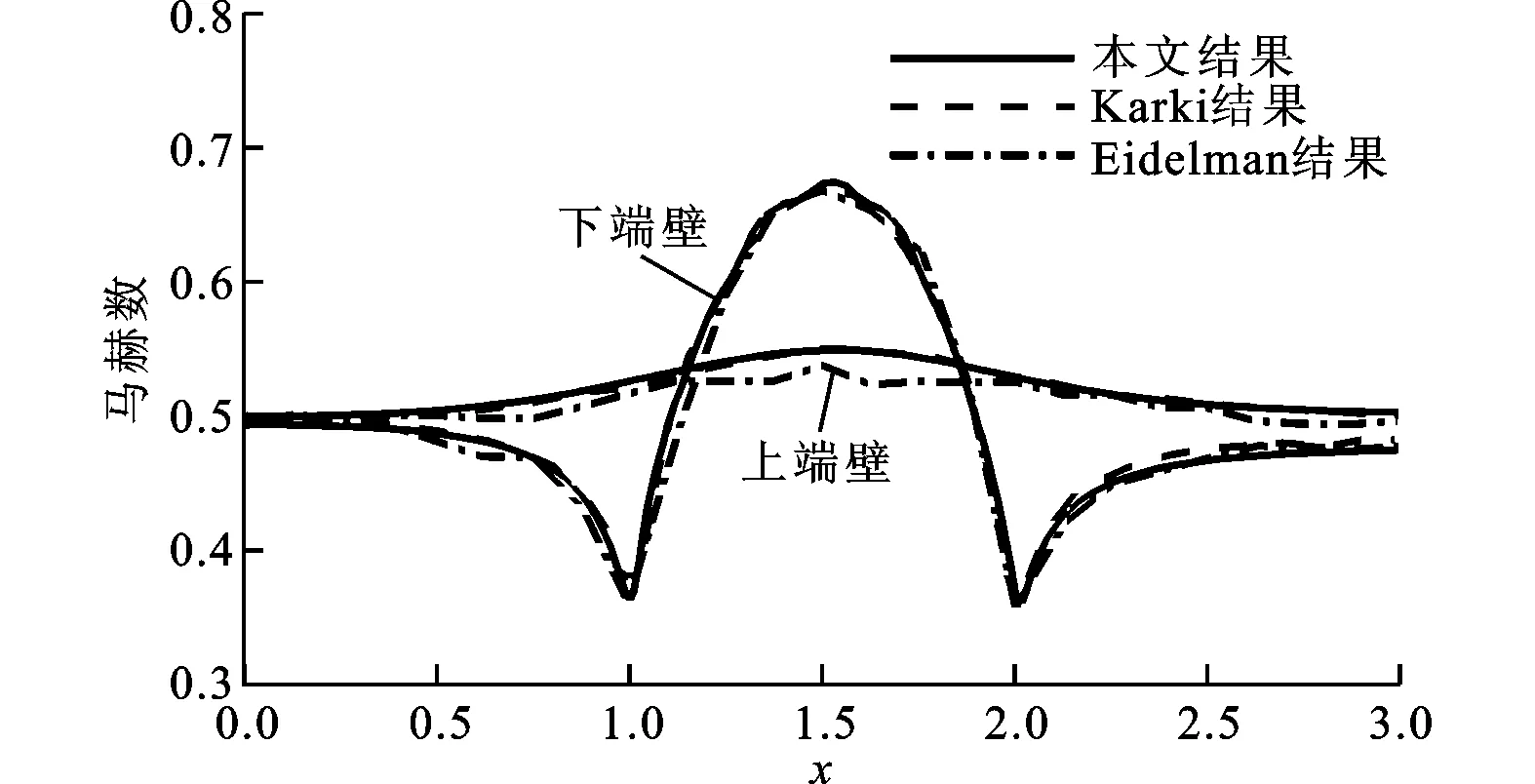
(a)亚音速

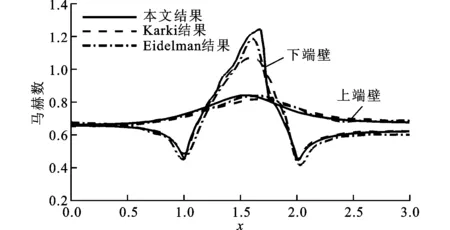
(b)跨音速

(c)超音速图4 3种工况下端壁处马赫数分布

(a)Numeca方法

(b)S2流面方法图5 Numeca方法和S2流面方法的计算网格

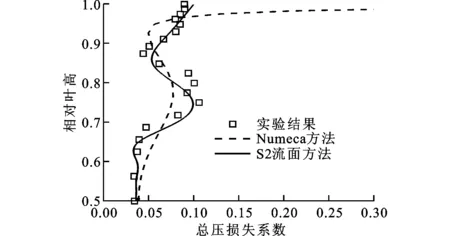
(a)总压损失系数

(b)马赫数

叶栅出口处马赫数约为0.22,沿径向变化较小,受65%～88%叶高处高损失的影响,该区域马赫数略有下降,但2种方法均可较好地捕捉该现象,与实验结果吻合良好。在叶栅出口处气流角约21°,径向分布均匀,且2种方法计算结果与实验结果误差也比较小,表明选用合理损失模型的S2流面方法对叶栅气动参数分布的计算精度较高,可用来进行低压涡轮性能预测。

(c)出口气流角图6 叶栅出口气动参数径向分布

2.3 三级低压涡轮计算结果与分析

将本文S2流面方法应用于某三级低压涡轮性能预测,并与全三维计算流体动力学(CFD)计算结果进行了对比,以评估多级环境下对涡轮总性能参数和气动参数的计算稳定性和可靠性。图7为Numeca方法和S2流面方法的计算网格。其中:Numeca方法计算网格总数约280万,计算设置同图5;S2流面方法计算网格轴向和径向节点数分别为241和27。计算时涡轮进口总压和总温分别为0.5 MPa和544 K,出口背压为72.0 kPa。

(a)Numeca方法

(b)S2流面方法图7 Numeca方法和S2流面方法的计算网格

表1为2种方法计算所得涡轮的总效率、流量、功率及计算耗时对比。相比于Numeca方法,S2流面方法计算所得总效率误差为-0.76%,流量与功率误差分别为0.75%和1.13%,表明S2流面方法对涡轮总性能参数具有较高的计算精度,计算结果较为可靠。采用多重网格加速的Numeca方法计算需要约18 h完成数值模拟,S2流面方法只需约3 min,且计算结果基本一致,可满足工业对涡轮设计准确性、快速性的要求。

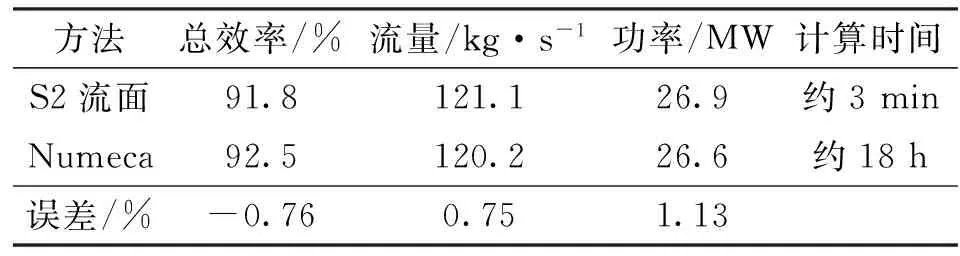
表1 2种方法总性能参数与计算时间对比

图8和图9为各级叶栅出口处气流角和马赫数的径向分布。S2流面方法计算所得各静叶、动叶出口的气流角、马赫数在径向分布趋势和数值大小等方面与Numeca方法吻合良好,表明本文方法在多级涡轮性能计算应用中能够合理计算各级叶栅流动参数,对气动参数分布计算的可靠性较高。

(a)第一级叶栅

(b)第二级叶栅

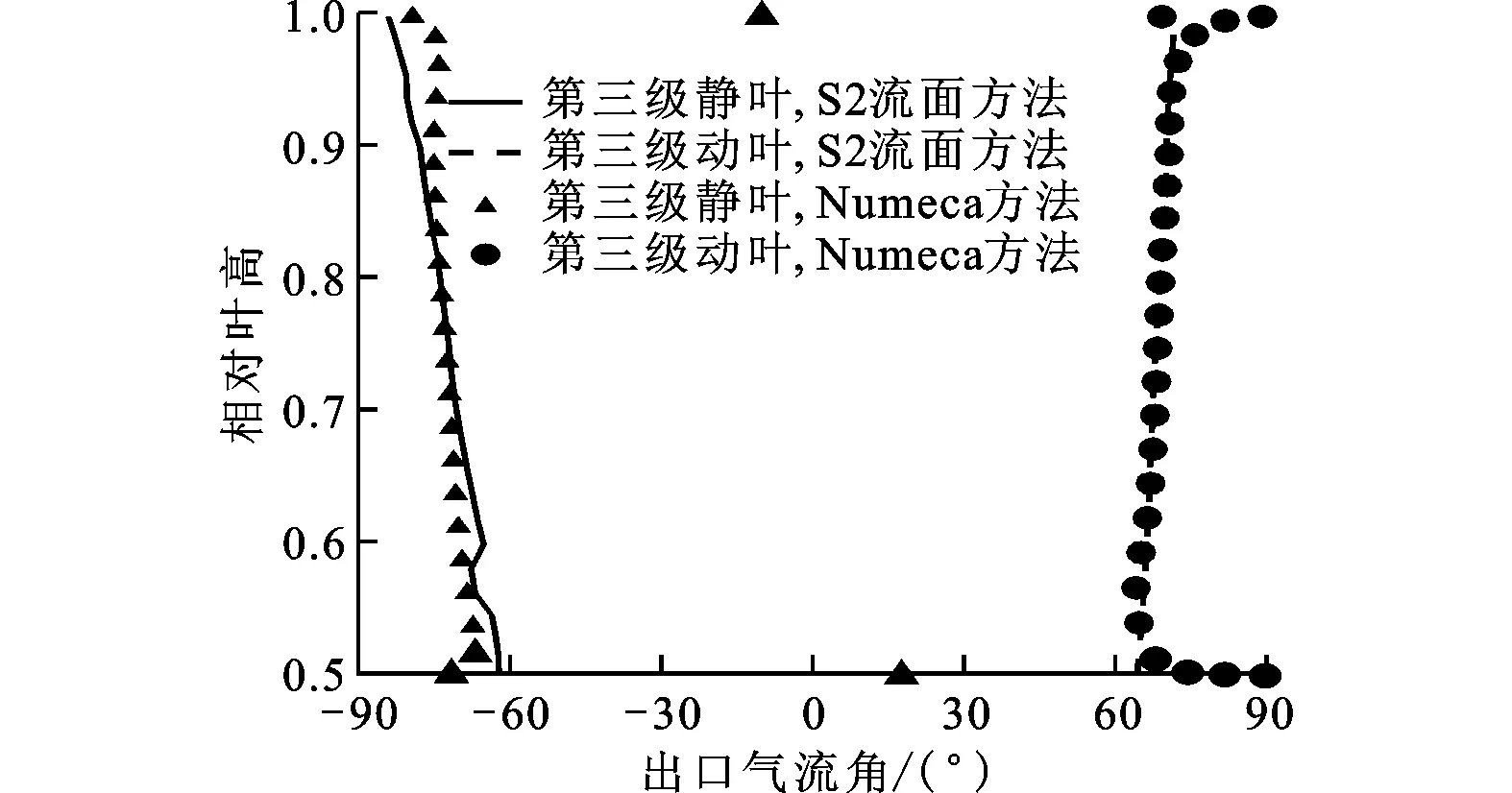
(c)第三级叶栅图8 各级叶栅出口处气流角的径向分布

图10为2种方法计算所得子午面马赫数分布云图。S2流面方法计算所得马赫数分布较为合理,且与三维黏性计算结果基本一致,如叶栅约束区域内气流加速的形式和位置都较接近,能够较准确地计算叶片三维几何形状对栅内流动参数的影响,表明本文方法能可靠计算多级涡轮内部流场参数分布,计算精度较高。

3 结 论

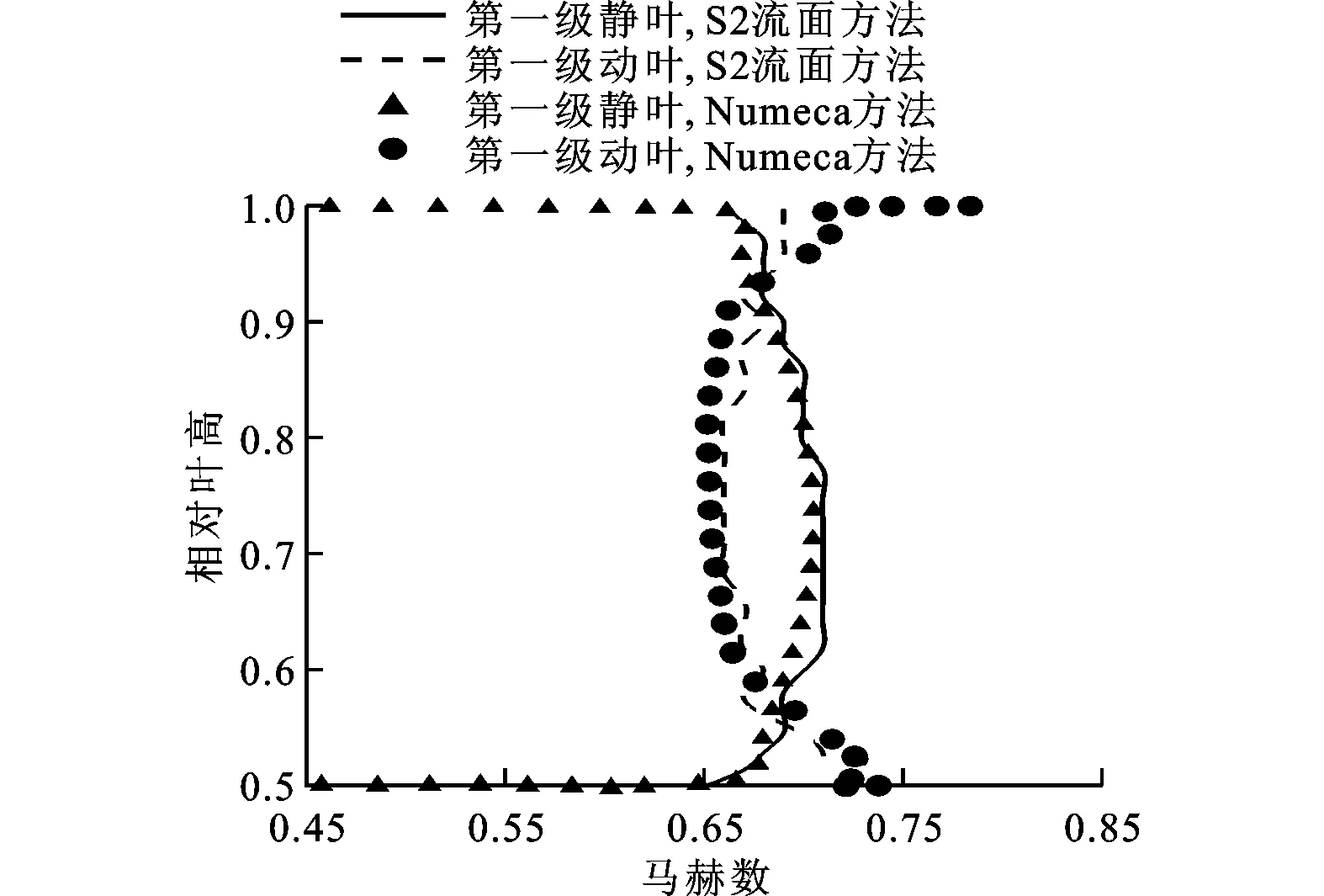
(a)第一级叶栅

(b)第二级叶栅

(c)第三级叶栅图9 各级叶栅出口处马赫数的径向分布

本文发展了一种基于Euler方程的S2流面的数值计算方法。为提高对涡轮叶栅复杂几何的适应能力,首先详细推导了任意正交曲线坐标系下的流动控制方程,给出了适用于S2流面各变换系数的具体形式,且应用非守恒型变量进行了求解,以避免守恒型波模型方程带来的压力波动,同时采用三阶精度的TVD格式进行了离散求解,推导了相应的数学模型,最后结合时间推进法和Riemann问题等完善了数值计算方法。

本文方法对流场中的激波捕捉分辨率较高,数值格式精度较为可靠。采用适当损失模型的S2流面方法能够合理预测栅内损失大小、分布及其对气动参数的影响,对叶栅气动参数计算精度比较高。在多级涡轮中的应用结果表明,S2流面方法能够在大大降低计算资源的前提下,保持与三维黏性计算结果相当的总性能参数计算准确度,并对叶栅出口处气动参数径向分布和子午面上参数分布也具有较高的计算精度。S2流面方法能够适应工程实际对涡轮设计的快速性和准确性的要求。

(a)S2流面方法

(b)Numeca方法图10 2种方法计算所得子午面马赫数分布云图

[1] WU Chunhua. A general theory of 3D flow in subsonic or supersonic turbomachines of axial, radial and mixed flow types, TN-2604 [R]. Washington DC, USA: NASA, 1952.

[2] 袁宁, 张振家, 顾中华, 等. 涡喷发动机压气机三种S2流面计算程序的比较 [J]. 推进技术, 1998, 19(1): 50-56. YUAN Ning, ZHANG Zhenjia, GU Zhonghua, et al. A comparison of three kinds of calculation program of S2 stream surface in the compressor of aero-engine [J]. Journal of Propulsion Technology, 1998, 19(1): 50-56.

[3] 程荣辉, 雷丕霓, 刘波, 等. 一种工程实用的多级轴流压气机特性二维数值计算方法 [J]. 航空动力学报, 2007, 22(6): 955-960. CHENG Ronghui, LEI Pini, LIU Bo, et al. A two-dimensional numerical method for multi-stage axial compressor performance in engineering applications [J]. Journal of Aerospace Power, 2007, 22(6): 955-960.

[4] 邵伏永, 杨金广, 刘振德, 等. 改进的流线曲率通流计算方法及在双涵道压缩系统设计中的应用 [J]. 航空动力学报, 2008, 23(6): 1073-1077. SHAO Fuyong, YANG Jinguang, LIU Zhende, et al. Improved streamline curvature throughflow method and its application in a bypass compression system design [J]. Journal of Aerospace Power, 2008, 23(6): 1073-1077.

[5] 高国荣, 苏莫明, 杨云凯. 轴流压缩机叶轮流线曲率法反问题的研究 [J]. 风机技术, 2009(5): 7-10. GAO Guorong, SU Moming, YANG Yunkai. Research on the inverse problem of streamline curvature method for axial-flow compressor impeller [J]. Compressor, Blower & Fan Technology, 2009(5): 7-10.

[6] 阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望 [J]. 力学进展, 2011, 41(5): 562-589. YAN Chao, YU Jian, XU Jinglei, et al. On the achievements and prospects for the methods of computational fluid dynamics [J]. Advances in Mechanics, 2011, 41(5): 562-589.

[7] 刘凤君, 王仲奇. 汽轮机次、末两级弯扭静叶的工程设计与实验研究 [J]. 工程热物理学报, 1996, 17(2): 161-165. LIU Fengjun, WANG Zhongqi. Engineering design and experiment study for the bowed and twisted blade in sub-last and last stages of steam turbine [J]. Journal of Engineering Thermophysics, 1996, 17(2): 161-165.

[8] 孙大伟, 乔渭阳, 许开富, 等. 低雷诺数条件下涡轮性能的计算研究 [J]. 航空动力学报, 2008, 23(7): 1253-1259. SUN Dawei, QIAO Weiyang, XU Kaifu, et al. Study on turbine performance at low Reynolds number [J]. Journal of Aerospace Power, 2008, 23(7): 1253-1259.

[9] SMADAR K. Multicomponent flow calculations by a consistent primitive algorithm [J]. Journal of Computational Physics, 1994, (112): 31-43.

[10]OSHER S, CHAKRAVARTHY S R. A new class of high accuracy TVD schemes for hyperbolic conservation laws [C]∥ AIAA Aerospace Sciences Meeting. Reston, VA, USA: AIAA, 1985: 0363.

[11]TORO E F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction [M]. 3rd ed. Berlin, Germany: Springer, 2009.

[12]李得英, 宋彦萍, 秦勇, 等. 基于二次函数的二次流损失模型研究 [J]. 工程热物理学报, 2013, 34(10): 1838-1841. LI Deying, SONG Yanping, QIN Yong, et al. Research of secondary flow loss model in term of quadratic function [J]. Journal of Engineering Thermophysics, 2013, 34(10): 1838-1841.

[13]KARKI K C, PATANKAR S V. Pressure based calculation procedure for viscous flows at all speeds in arbitrary configurations [J]. AIAA Journal, 1989, 27(9): 1167-1182.

(编辑 苗凌)

Euler S2 Stream Surface Calculation for Arbitrary Curvilinear Coordinate System

LI Deying1,SONG Yanping1,CHEN Fu1,ZHENG Zhenjiang1,2,CHEN Huanlong1

(1. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China;2. The 31st Research Institute, China Aerospace Science and Industry Corp., Beijing 100074, China)

To adapt the complex geometry of the turbine profile and improve the computing capability, an Euler S2 stream surface calculation strategy is proposed in the body-fitted coordinate system, the governing equation for Euler S2 stream surface calculation in the arbitrary orthogonal curvilinear coordinate system is derived in detail, and the mathematical model for the third order total variation diminishing (TVD) difference scheme is developed. The implicit time marching method and the Riemann solver are also employed to solve the aerodynamic parameters of a flow channel with bump and a linear cascade, and to predict the performance of a 3-stage low pressure turbine. The results show that the proposed strategy is able to capture the shock wave with high resolution. The solution to the linear cascade coincides well with the experimental data with a credible accuracy for the flow field calculation.

S2 stream surface calculation method; Euler equation; arbitrary orthogonal curvilinear coordinate system; total variation diminishing difference scheme; low pressure turbine

2014-11-29。

李得英(1988—),男,博士生;宋彦萍(通信作者),女,教授。

国家自然科学基金委创新研究群体基金资助项目(51121004);国家自然科学基金资助项目(50976026)。

时间:2015-04-27

10.7652/xjtuxb201507008

TK14

A

0253-987X(2015)09-0042-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150427.1754.007.html