气凝胶及其纤维复合材料等效导热系数预测

方文振,粘权鑫,张虎,陈黎,陶文铨

(西安交通大学热流科学与工程教育部重点实验室, 710049, 西安)



气凝胶及其纤维复合材料等效导热系数预测

方文振,粘权鑫,张虎,陈黎,陶文铨

(西安交通大学热流科学与工程教育部重点实验室, 710049, 西安)

为了研究气凝胶及其纤维复合材料的隔热性能,分别数值重构了几种气凝胶及其纤维复合材料的微细观随机结构,采用格子Boltzmann方法数值求解了它们的等效导热系数,同时用基于瞬态平面热源法的Hot Disk热常数分析仪测量了它们在复杂环境下的等效导热系数。研究表明:骨架连续的开孔型微观结构比骨架不连续的颗粒型微观结构更符合气凝胶的实际结构,开孔型结构等效导热系数的数值预测值与实验值的偏差大部分在±10%内;气凝胶的密度值会影响它的隔热性能,且存在着最佳的密度使得气凝胶的等效导热系数最低;纤维复合气凝胶的等效导热系数随着纤维体积分数的增加而增加;纤维在垂直于热流方向的水平面内随机排布时对气凝胶的隔热性能影响最小。

气凝胶;数值重构;等效导热系数;格子Boltzmann方法

SiO2气凝胶是一种典型的纳米多孔绝热材料,质量轻且导热系数极低,因而广泛应用于航空航天等领域中[1]。但是,SiO2气凝胶的孔隙率极高、比表面积极大、密度极低,空间结构高度复杂。Zeng等用交叉立方球单元体模型计算了气凝胶的等效导热系数[2];Xie等用分形理论来预测气凝胶的等效导热系数[3];Wei等提出一种面接触空心立方结构模型来研究硬硅酸钙型SiO2气凝胶的等效导热性能[4];Dan等提出一种中空球结构模型来研究气凝胶在不同环境下的等效导热系数[5]。

纯气凝胶易脆且强度极低,实际使用中常加入纤维来提高其力学性能。为研究纤维的影响,Lu等用长方体单元体模型来研究纤维的影响,其中长方体的各个棱柱代表纤维[6];Xie等分别用Hamilton模型和串联模型来计算纤维增强复合材料的等效导热系数[3];Zhao等用串并联混合公式来研究纤维的加入对气凝胶等效导热系数的影响[7]。

上述预测气凝胶及其纤维复合材料等效导热系数的方法虽然简便,但都忽略了随机结构对等效导热系数的影响。本文首先数值重构了气凝胶的微观随机结构,基于格子Boltzmann方法计算纯气凝胶的等效导热系数;在获得纯气凝胶等效导热系数的基础上,再重构出纤维随机排布时的单元体结构来获得纤维复合气凝胶的等效导热系数;最后利用基于瞬态平面热源法[8]的Hot Disk实验台测试了气凝胶的等效导热系数,验证了该方法的合理性。

1 等效导热系数数值预测模型

1.1 数值重构微细观结构

图1是气凝胶及纤维增强复合气凝胶的微观结构电镜图。气凝胶的结构高度复杂,为更好地重构出符合气凝胶实际的微观结构,这里分别重构了骨架不连续的颗粒型[9]和骨架连续的开孔型[10]两种不同的微观结构(见图2)来做比较。为研究纤维的排布方向对气凝胶等效导热系数的影响,这里重构了3种不同纤维排布方向的单元体结构[11],其中图3a是纤维在垂直于热流方向的水平面内随机排布的结构图,图3b是纤维与水平面的夹角在±30°范围内随机排布的结构图,而图3c是纤维与水平面的夹角在±90°范围内随机排布(即空间随机分布)的结构图。

(a)气凝胶 (b)纤维增强复合气凝胶图1 气凝胶及纤维增强复合气凝胶的电镜图

(a)颗粒型 (b)开孔型 图2 重构的气凝胶微细观结构

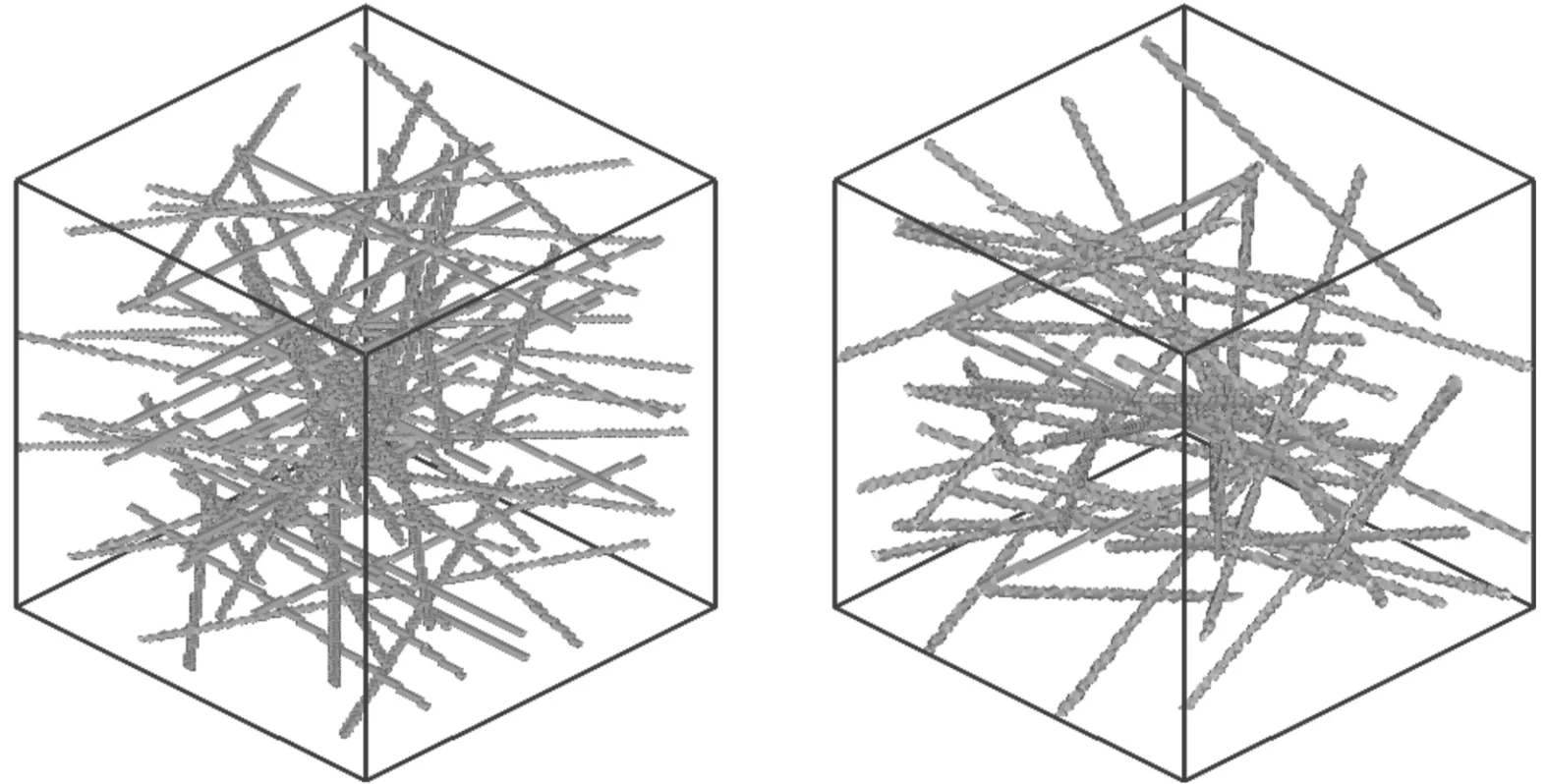
(a)纤维平行于水平面 (b)纤维与水平面夹角在±30°内

(c)纤维空间随机排列图3 重构的纤维增强复合气凝胶微细观结构

1.2 数值重构微细观结构

气凝胶及其复合材料中的传热形式包含导热和辐射。本文采用格子Boltzmann方法来求解气凝胶及其复合材料由于导热引起的气固耦合导热系数。对于纯导热问题,可采用D3Q7的格子模型来求解。对于两相组分的材料而言,如气凝胶中的气相和固相(对于纤维增强复合气凝胶,两相组分分别为纯气凝胶和纤维),它们对应于导热控制方程的温度分布函数演化方程可以表示为[9]

(1)

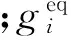
(2)

ei是格子离散速度

(3)

对于气凝胶中的气相和固相,其演化方程中的松弛因子与宏观导热系数的关系[12]为

(4)

式中:λg、λs分别为气凝胶中气相、固相的导热系数;c是格子速度,理论上可取任何值,只需保证τ在(0.5,2)之间[12]。

为保证热流和温度在相界面上连续,应满足如下的关系式[12]

(5)

而宏观温度可由温度分布函数求和来获得

(6)

在获得收敛之后的稳定温度场后,可由下式来计算由于导热引起的热流密度[10]

(7)

那么,材料的气固耦合导热系数为

(8)

式中:Nx是x方向上的格点数。在进行数值求解时,需要给定求解区域的边界条件,这里对单元体的上下壁面给定等壁温边界条件,而四侧面绝热。相应的边界条件在格子Boltzmann方法中的处理过程见文献[9,13-14]。

气凝胶的辐射导热系数可由下式计算得到[4]

(9)

式中:ρ是气凝胶密度;βm为平均消光系数,可由文献[4]中的光谱消光系数得到

(10)

对于气凝胶,其等效导热系数是气固耦合导热系数和辐射导热系数之和

(11)

要计算复合材料的等效导热系数,首先要确定各组分的导热系数。Zeng等给出了气凝胶孔隙中气体导热系数的计算公式[15]

(12)

而气凝胶的比表面积为[3]

(13)

气凝胶的孔隙率为

(14)

式中:ρbulk是SiO2块材密度。

本文中SiO2气凝胶固体导热系数取为块材的1.34 W/(m·K)[16],SiO2纤维的导热系数也为1.34 W/(m·K)。

2 导热系数实验测试

本文采用基于瞬态平面热源法的Hot Disk法测试复杂环境下导热系数的测试实验台。该实验台可以调节的压力范围为0.01 Pa～1 MPa,温度为室温到1 000 K,实验系统的示意图[17]如图4所示。

图4 实验系统示意图

该实验台的精度经校准后,在测试室温下导热系数为0.032 W/(m·K)的NIST1453聚苯乙烯板标准材料时,偏差在±1.5%。实验原理可参考文献[17]。本文测试了密度为350 kg/m3的气凝胶在常温、不同压力下的等效导热系数和不同纤维含量复合气凝胶的等效导热系数。测试样品的大小约为45 mm×45 mm×16 mm,瞬态测试过程中温差不超过2 K,测试所用的探头为Kapton5501探头。

3 结果与讨论

气凝胶的微细观结构与其等效导热系数的大小有着密切的联系。本文重构出颗粒型和开孔型两种不同的气凝胶微细观结构(见图2),基于格子Boltzmann方法数值计算了这两种结构在不同压力下的等效导热系数,并与实验值进行了对比,对比结果如图5所示。从图5中可以看出,在压力低于1 kPa时,颗粒型微细观结构所计算得到的等效导热系数趋近于0,而开孔型微细观结构所计算得到的等效导热系数与实验值符合较好。其原因在于:对于颗粒型的微细观结构,颗粒骨架不连续,当压力很低时,气体导热系数趋近于0,而此时固相是不连续的,无法形成导热通道,故当压力趋近于0时,该等效结构计算得到的导热系数趋近于0;对于开孔型的微细观结构,颗粒骨架是连续的,即使当气体导热系数趋近于0时,能量还是可以通过连续的骨架进行传递,因此导热系数不趋于0,而是趋于0.019 W/(m·K)。从图5中还可以看出,开孔型微细观随机结构计算得到的等效导热系数与实验值符合良好,大部分相对误差都在±10%之内,可用来近似代替气凝胶的结构(在这之后的数值计算结果都是基于开孔型的微细观随机结构获得的)。

图5 不同压力下气凝胶等效导热系数实验值与模拟值的对比

3.1 密度的影响

为研究气凝胶的密度(孔隙率)对气凝胶等效导热系数的影响规律,本文计算了在T=300 K、气凝胶不同密度时各导热系数的大小,如图6所示。

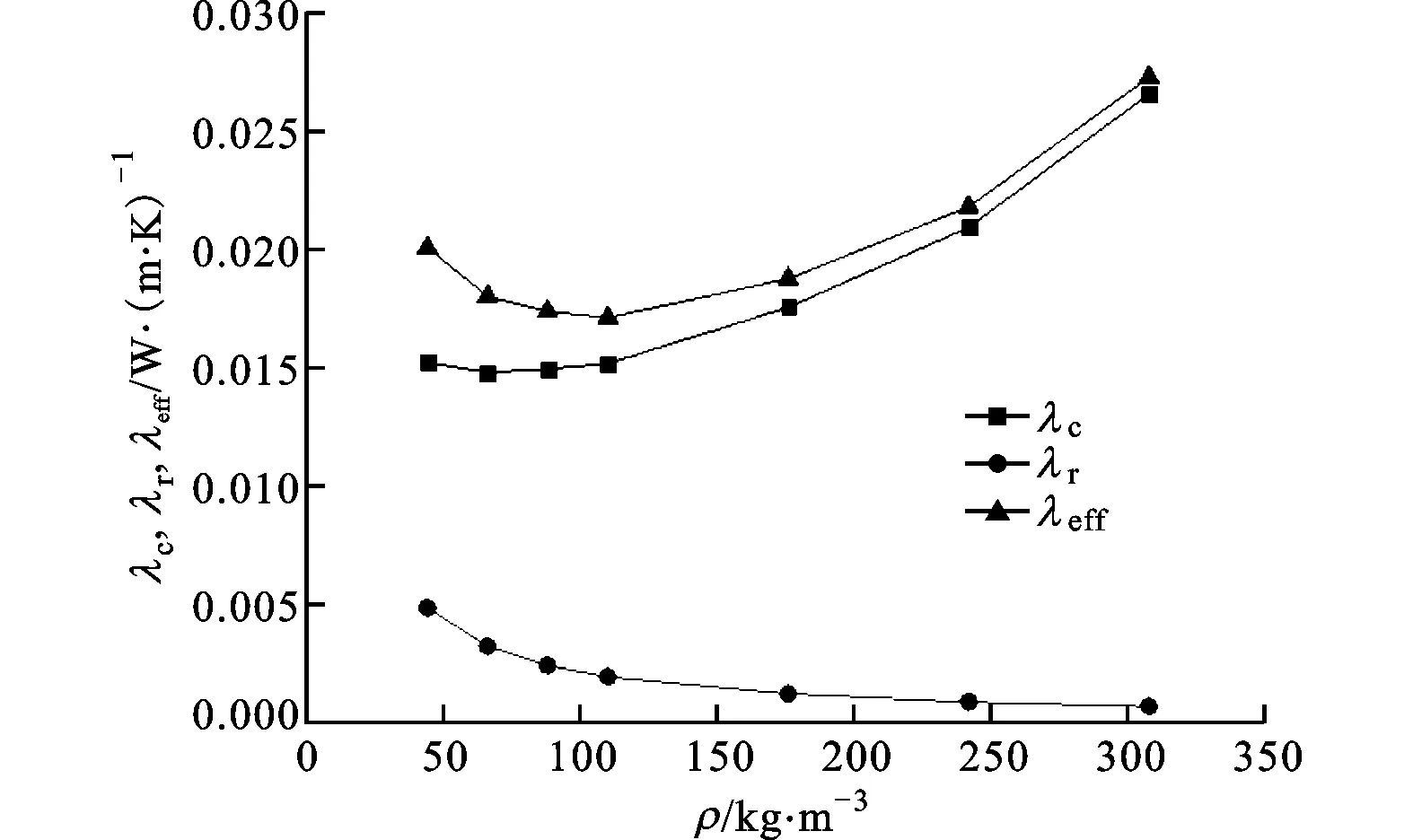
图6 密度对气凝胶各导热系数的影响

从图6中可以看出,辐射导热系数随着气凝胶密度的增加而降低,而气固耦合导热系数随着密度的增加略微下降后增加,因而存在一个最佳的密度值(约为110 kg/m3)使得气凝胶的等效导热系数最小。Wei等通过实验得到最佳的SiO2气凝胶的密度在110～160 kg/m3的范围内[4]。不同研究者所获得的最佳密度值存在波动,这和所选取的气凝胶固体导热系数以及计算等效导热系数时所采用的微结构模型有很大关系。由于本文没有对气凝胶的固体导热系数做出纳米尺寸效应修正,所选取的气凝胶固体导热系数偏大,因而计算得到的最佳密度值会偏小。采用何种方法来修正重构结构中气凝胶固体的导热系数,值得进一步研究。

3.2 纤维的影响

为研究纤维的体积分数对复合气凝胶隔热性能的影响规律,实验测量了纤维体积分数为0.17%、0.51%、0.87%、1.25%时复合气凝胶的等效导热系数(材料孔隙率为0.838,纯气凝胶基体的等效导热系数为0.033 1 W/(m·K));为研究纤维排布方式的影响,分别模拟计算了纤维在垂直于热流方向的水平面内,纤维与水平面夹角在±30°、±90°内随机排布(见图3)时气凝胶的等效导热系数。图7给出了它们的对比结果。

图7 不同纤维体积分数时复合气凝胶等效导热系数的对比

从图7中可以看出:复合气凝胶的等效导热系数随着纤维体积分数的增加而增加,但纤维的加入并没有显著影响气凝胶的隔热性能,纤维体积分数为1.25%的等效导热系数比纤维体积分数为0.17%时提高了7%(实验值);当纤维垂直于热流方向放置时,纤维的加入几乎不提高复合气凝胶的等效导热系数,因为纤维被气凝胶基体很好地隔绝了;当纤维在空间随机排布时,平行于热流方向的纤维比例增大,因而纤维的加入较明显地提高了复合气凝胶的等效导热系数;当纤维与垂直于热流方向的水平面的夹角在±30°范围内随机变化时,复合气凝胶的等效导热系数与实验值符合得相对较好。因而,如果要避免纤维的加入显著提高复合气凝胶的等效导热系数,应尽量使纤维在垂直于热流方向的水平面内布置。

4 结 论

(1)骨架连续的开孔型结构比骨架不连续的颗粒型微细观结构模型更符合气凝胶的实际结构,用格子Boltzmann方法对开孔型微细观结构计算得到的等效导热系数与实验值的偏差大都在±10%内,可用来近似代替纯气凝胶的复杂空间结构。

(2)气凝胶的密度会影响气凝胶的等效导热系数,且存在最佳的密度值使得气凝胶等效导热系数最小。

(3)气凝胶的等效导热系数随着纤维体积分数的增加而增加,但纤维体积分数不是影响气凝胶等效导热系数的主导因素。

[1] HÜSING N, SCHUBERT U. Aerogels-airy materials: chemistry, structure, and properties [J]. Angewandte Chemie: International Edition, 1998, 37(12): 22-45.

[2] ZENG S Q, HUNT A, GREIF R. Geometric structure and thermal conductivity of porous medium silica aerogel [J]. Journal of Heat Transfer, 1995, 117(4): 271-277.

[3] XIE T, HE Y L, HU Z J. Theoretical study on thermal conductivities of silica aerogel composite insulating material [J]. International Journal of Heat and Mass Transfer, 2013, 58(1/2): 540-552.

[4] WEI G S, LIU Y, ZHANG X, et al. Thermal conductivities study on silica aerogel and its composite insulation materials [J]. International Journal of Heat and Mass Transfer, 2011, 54(11/12): 2355-2366.

[5] DAN D, ZHANG H, TAO W Q. Effective structure of aerogels and decomposed contributions of its thermal conductivity [J]. Applied Thermal Engineering, 2014, 72(1): 2-9.

[6] LU G, WANG X D, DUAN Y Y, et al. Effects of non-ideal structures and high temperatures on the insulation properties of aerogel-based composite materials [J]. Journal of Non-Crystalline Solids, 2011, 357(22/23): 3822-3829.

[7] ZHAO J J, DUAN Y Y, WANG X D, et al. Radi-ative properties and heat transfer characteristics of fiber-loaded silica aerogel composites for thermal insulation [J]. International Journal of Heat and Mass Transfer, 2012, 55(19/20): 5196-5204.

[8] International Organization for Standardization. ISO 22007-2: 2008(E) Plastics: determination of thermal conductivity and thermal diffusivity Part 2 Transient plane heat source method [S/OL]. [2014-12-10]. http: ∥www.iso.org/iso/home/store/catalogue_tc/catalogue_detail.htm?csnumber=40683.

[9] WANG M, WANG J, PAN N, et al. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media [J]. Physical Review: E, 2007, 75(3): 036702.

[10]WANG M, PAN N. Modeling and prediction of the effective thermal conductivity of random open-cell porous foams [J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1325-1331.

[11]WANG M, KANG Q, PAN N. Thermal conductivity enhancement of carbon fiber composites [J]. Applied Thermal Engineering, 2009, 29(2/3): 418-421.

[12]XUAN Y M, ZHAO K, LI Q. Investigation on mass diffusion process in porous media based on Lattice Boltzmann method [J]. Heat and Mass Transfer, 2010, 46(10): 1039-1051.

[13]HE Y L, WANG Y, LI Q. Lattice Boltzmann method: theory and applications [M]. Beijing, China: Science Press, 2009.

[14]MOHAMOD A A. Lattice Boltzmann method [M]. New York, USA: Springer, 2011.

[15]ZENG S Q, HUNT A, GREIF R. Mean free path and apparent thermal conductivity of a gas in a porous medium [J]. Journal of Heat Transfer, 1995, 117(3): 758-761.

[16]WANG M R, WANG X, WANG J, et al. Grain size effects on effective thermal conductivity of porous materials with internal thermal contact resistance [J]. Journal of Porous Media, 2013, 16(11): 1043-1048.

[17]方文振, 张虎, 屈肖迪, 等. 遮光剂对气凝胶复合材料隔热性能的影响 [J]. 化工学报, 2014, 65(S1): 168-174. FANG Wenzhen, ZHANG Hu, QU Xiaodi, et al. Influence of opacifiers on thermal insulation properties of composite aerogels [J]. CIESC Journal, 2014, 65(S1): 168-174.

(编辑 荆树蓉)

Prediction of the Effective Thermal Conductivity of Aerogel and Its Fiber-Loaded Composites

FANG Wenzhen,NIAN Quanxin,ZHANG Hu,CHEN Li,TAO Wenquan

(Key Laboratory of Thermo-Fluid Science and Engineering of MOE, Xi’an Jiaotong University, Xi’an 710049, China)

Different random microstructures of aerogels and their fiber-loaded composites were numerically reconstructed to investigate their insulation performances. The lattice Boltzmann method was adopted to calculate their effective thermal conductivities. Some experimental measurements based on the hot disk method were conducted to determine the effective thermal conductivities of the aerogels at different pressures. The results show that: the open-cell microstructure with continuous skeleton is more suitable for the real structure of the aerogel than the granular microstructure with discontinuous skeleton; the predictions of the effective thermal conductivities based on the open-cell structure agree well with the experimental data, and the deviations are within ±10%; the density of aerogels affects their effective thermal conductivities, and there exists an optimal density value to minimize the effective thermal conductivity of a aerogel; the effective thermal conductivities of the aerogel composites increase with the fiber doping concentration; the increment of the effective thermal conductivity of the fiber-load aerogel is the lowest when the fibers are laid in the plane vertical to heat flux.

aerogel; numerical reconstruction; effective thermal conductivity; lattice Boltzmann method

2015-01-31。

方文振(1990—),男,博士生;陶文铨(通信作者),男,教授,博士生导师,中国科学院院士。

国际合作重点基金资助项目(51320105004)。

时间:2015-04-21

10.7652/xjtuxb201507005

TK311

A

0253-987X(2015)07-0025-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150421.1711.005.html