2015 年高考江苏数学卷19 题解法探究
2015-02-24朱允洲
朱允洲
(江苏省徐州高等师范学校)
朱允洲
(江苏省徐州高等师范学校)
题目:已知函数f(x)=x3+ax2+b(a,b∈R),
(1)试讨论f(x)的单调性;
(2)若b=c-a(实数c 是与a 无关的常数),当函数(fx)有三个不同的零点时,a 的取值范围恰好是(-∞,-3)∪(1)∪(,+∞),求c 的值。
本题考查了函数的零点、导数的运算、函数的极值等知识,涉及函数与方程、数形结合和分类讨论以及化归与转化的数学思想,同时考查了学生对多参数问题的分析处理的能力。下面给出几种与标准答案不同的解法。
解(1)略
(2)法1:显然,a=0 不合题意。对(fx)求导,f(′x)=3x2+2ax,令f(′x)=0,得x=0,或x=-,易知0,-是函数的两个极值点,函数(fx)有三个不同的零点⇔(f0)·(f-)<0,即(a-c)(a3-a+>0,因为此不等式的解集恰好为(-∞,-3)∪(1,∪,+∞),此处求解可有两种思路:
思路一 (方程法)
方程(a-c)(a3-a+c)=0 的根应为:a=-3,1,(二重根),将它们带入方程得:c=-3,1,经检验只有c=1 时,上述方程的解为:-3,1。
思路二 (待定系数法)
当c=1 时,(fx)=x3+ax2+1-a=(x+1)(a-1)x+1-a因(fx)有三个不同的零点,故x2+(a-1)x+1-a=0 有两个异于-1 的根,于是由Δ>0 及1+(a-1)(-1)+1-a≠0,得a 的取值范围(-∞,-3)∪(1,)∪,+∞)。综上,c=1。
法2:由x3+ax2+1-a=0,得x3+ax2=a-c,令p(x)=x3+ax2,q(x)=ac,函数(fx)有三个不同的零点,等价转化为两函数p(x)与q(x)的图象有三个不同的交点。p(′x)=3x2+2ax,令p(′x)=0,得x=0,或x=-,且易知其为p(x)的两个极值点,①当a>0 时,p(x)极大值=p(-=-,p(x)极小值=p(0)=0,应有0<a-c<,即a-<c<a 恒成立,∀a∈(1)∪(,+∞),于是(a-)max<c<amin,即1≤c≤1,所以c=1。②当a<0 时,p(x)极大值=p(0)=0,p(x)极小值=p=,应有<a-c<0,即a<c<a-恒成立,∀a∈(-∞,-3),于是amax<c<(a-min,即-3≤c≤1。综上,由①②得c=1,经检验c=1满足题意。
法3:设函数(fx)=x3+ax2-a+c,由f(′x)=0,得x=0,或x=-,当a>0 时,(fx)极大值=-a+c,f(x)极小值=c-a;当a<0 时,f(x)极小值=-a+c,(fx)极大值=c-a。令h(a)=-a,易知其图象关于原点对称(如图),且h(=-1,h=0。将h(a)的图象上下平移个单位,有:
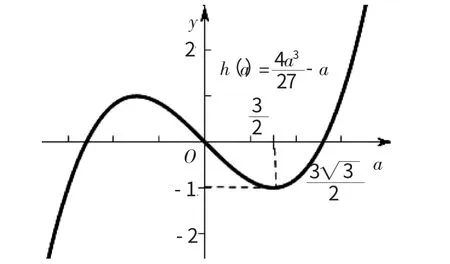

函数(fx)有三个零点等价于[h(a)+c]·(c-a)<0。考虑a<0 情况,由h(a)<0 得:a∈(-∞,-,而h(a)+c=-a+c<0 的解集为(-∞,-3)(**),由(*)式知由h(a)向上平移c 个单位,同时ca>0。由(**)式知-3 为方程-a+c=0 的根,得c=1,将c=1 带入原函数(fx)检验符合题意。
注:
1.由h(a)图象平移的对称性知:当函数(fx)有三个不同的零点时,若a∈(-∞,-∪(-,-1)∪(3,+∞),则c=-1;特别地,若a∈(-∞,-,+∞),则c=0;
2.若函数(fx)有三个不同的零点,将h(a)的图象向上平移(c>0)个单位与向下平移个单位,则a 的取值范围关于原点对称。
