一类特殊四面体的探究

林龙英

（广东省佛山市顺德区中等专业学校）

我们知道直角三角形在三角形当中是一类特殊的三角形，具有很大的研究价值，得到了很多有用的结论。那么在推广到三维空间，在所有的四面体中也有一类比较特殊的四面体叫做直四面体，经常在各类高考模拟考试中出现，本文对其进行探讨，得到一些重要的结论.

直四面体的定义：如图1 所示，在四面体P-ABC 中，侧棱PA，PB，PC 两两相互垂直，我们称这样的四面体为直四面体，以下是基于直四面体的研究得到的结论.

图1

一、海伦公式的变形

引理：在△ABC 中∠A，∠B，∠C 所对的边长分别为a，b，c，s=，S 表示△ABC 的面积，则有S=；我们称为海伦公式，对其进行等价变形后会得到一些等价的形式。

二、结论

为了研究方便，如图2 假设直四面体P-ABC 的侧棱PA，PB，PC 的长度分别为m，n，t，容易证明PA⊥面PBC，PB⊥面PAC，PC⊥面PAB；三角形PBC，PAC，PAB 都是直角三角形.

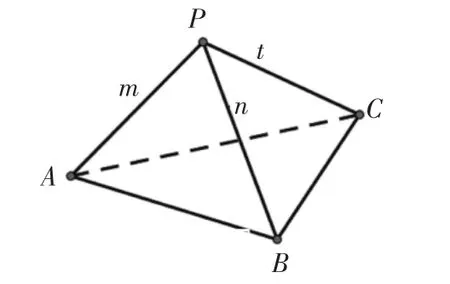
图2

结论1：S2PAB+S2PBC+S2PAC=S2ABC

证明：∵侧棱PA，PB，PC 的长度分别为m，n，t，且三角形PBC，PAB，PAB 都是直角三角形.

∴SPAB=mn；SPBC=nt；SPAC=mt；

结论2：假如在棱AB，BC，AC 边上分别取中点D，E，F，如图3则有：S2PDC+S2PAE+S2PBF=2S2ABC

图3

证明：∵D 是AB 的中点，且△PAB 是直角三角形；

∴SPDC=·t；

同理可得：SPAE=·m；SPBF=

由前面可知：SABC=

即S2PDC+S2PAE+S2PBF==2S2ABC

结论3：假如在结论2 中的棱AB，BC，AC 边上的中点D，E，F 分别改为棱AB，BC，AC 的垂足，则有：

证明：∵△PAB 是直角三角形，对△PAB 的面积算两次即，

∵PC⊥面PAB；∴PC⊥PD；∴△PDC 是直角三角形；∴SPDC=PD·

同理可得：SPAE=

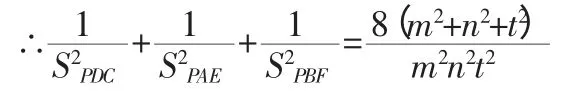
结论4：假设如图4 侧面PAB，PBC，PAC 与底面ABC 的二面角分别为α，β，γ，则有sin2α+sin2β+sin2γ=2；cos2α+cos2β+cos2γ=1.

图4

证明：如图4 所示，作PO⊥面ABC 于点O；对四面体的体积算两次，即VP-ABC=S△ABC·PO=S△PAB·PC，由前面可知SABC=

∴sin2α=

同理可得：sin2β=

∴sin2α+sin2β+sin2γ==1；

cos2α+cos2β+cos2γ=3-（sin2α+sin2β+sin2γ）=3-1=2

证明：将四面体P-ABC 补全为长方体（如图6 所示）；则四面体的外接球与长方体的外接球相同，而长方体的外接球半径R=（证明略），所以直四面体的外接球半径R=

即，sin2α=，

同理可得：sin2β=，sin2γ=

cos2α+cos2β+cos2γ=3-（sin2α+sin2β+sin2γ）=3-2=1

结论5：如果四面体的三条棱PA，PB，PC 分别与底面ABC 所称的角分别记为α，β，γ（如图5），则sin2α+sin2β+sin2γ=1；cos2α+cos2β+cos2γ=2

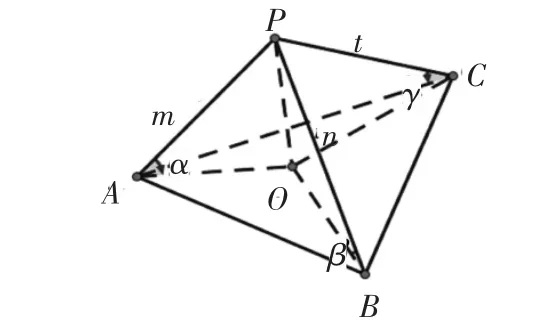
图5

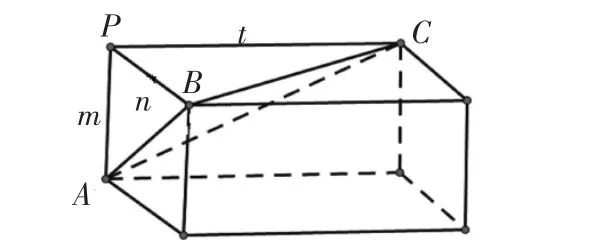
图6

假设内接球的半径为r，对四面体的体积算两次，

徐晨，陆智明，罗华，等.对一个特殊四面体性质的研究［J］.中学理科，2000（09）.